水下超声波测距误差补偿方法研究

何鸣飞，王利恒

（武汉工程大学 电气信息学院，武汉430205）

超声波测量是一种利用超声波的反射特性进行距离测量的非接触式测量方式。超声波不易受到外界色彩、光线明暗和电磁场的干扰，即使被测物处于光照条件差、灰尘烟雾较多、强电磁干扰等恶劣的测量环境下，也能有较高的分辨力[1]。超声波测量广泛应用于建筑工程行业测量、中短距离物体辨识等方面。在测距方面，由于超声波在液体和气体这2 种介质中的传播速度均较慢、波长较短，可看成直线传播，不仅衰减较小，方向性好，而且能量易于集中，因此反射信号中的传播信息很容易被识别检测出来。超声波发射器结构也较为简单、体积小，容易提高其抗干扰能力。

影响超声波测距精度的因素较多，包括温度、深度、反射面光滑程度、频率、盲区、换能器特性、多径效应等。在深海测量环境下，随着深度的大幅增加，压力和温度都会发生较大改变，声速也会随之改变，对测距的结果产生影响。故在此重点探讨水下测距时温度、深度、频率及多径效应对测距的影响。

1 超声波测距误差分析及建模

谐振频率高于20 kHz 的声波称为超声波。目前超声波测距的常用方法有声波幅值检测法、相位检测法和渡越时间检测法。声波谐振频率高于20 kHz的声波称为超声波。目前，超声波测距的常用方法有声波幅值检测法、 相位检测法和渡越时间检测法。声波幅值检测法仅能用于特定的反射介质，相位检测法虽然测量精度高但测量距离短，因此通常采用渡越时间检测法进行超声波测距。其原理是由超声波换能器发射超声波，超声波在介质中传播遇到障碍物反射回来，通过计算超声波在介质中的传播时间，即可求出发射点与反射点之间的距离[2]。有参数见表1[4]。在压强101．325 kPa 条件下，温度与声速的关系如图1 所示；当T＝20 ℃时深度与声速的关系如图2 所示。

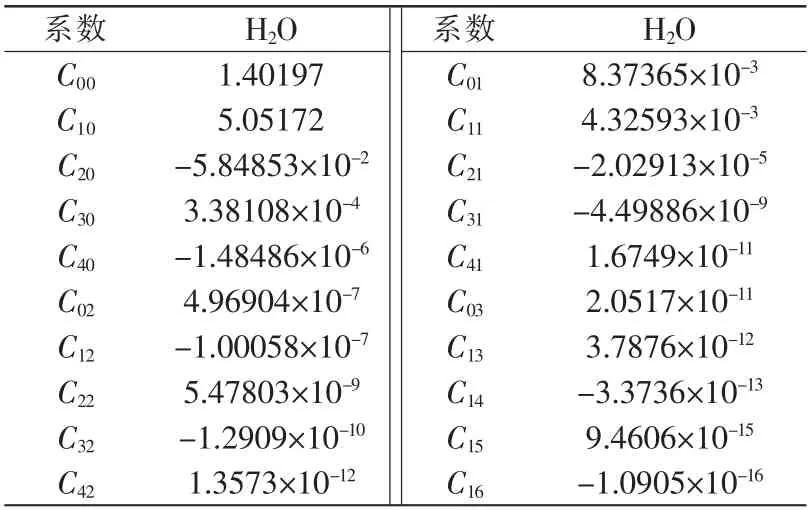
表1 非零系数Tab.1 Non-zero coefficients

式中：d为超声波换能器到被测物体的距离；t为渡越时间；v为声波在介质中的传播速度。声音的传播受到介质的影响会产生衰减，其速度与介质的弹性模量成正比。为描述液体的声学性质，引入了传播常数，即

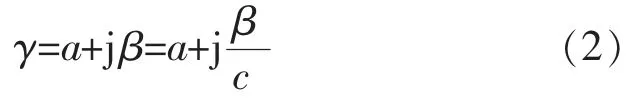
式中：ω 为角频率；c为平面行波中的相速度；a为衰减常数。故液体的声学性质可以用c和a来描绘。这2 个量一般为频率、压力和温度的函数。a根据其物理含义可分为2 个部分，经典衰减和逾量衰减。经典衰减a1与介质的黏滞性和热传导性有关，正比于频率的平方；逾量衰减a2与液体的弛豫机理有关，在大部分情况下弛豫时间都相当短，可以认为a2也与频率的平方成比例。那么，仅用a/f2和c这2 个物理量就可以描述不同液体在不同温度下的特性。

醇类和水a/a1＜4，且其衰减常数为负温度系数，属于缔合液体。可认为a/f2和c均不随频率变化，且由于超声波的频率远高于气泡的共振频率，故不考虑气泡腔体的热效应[3]。

在大深度环境下，由于深度的大幅增加，压力和温度的变化量都较大。对于温度、压强和声速的关系为

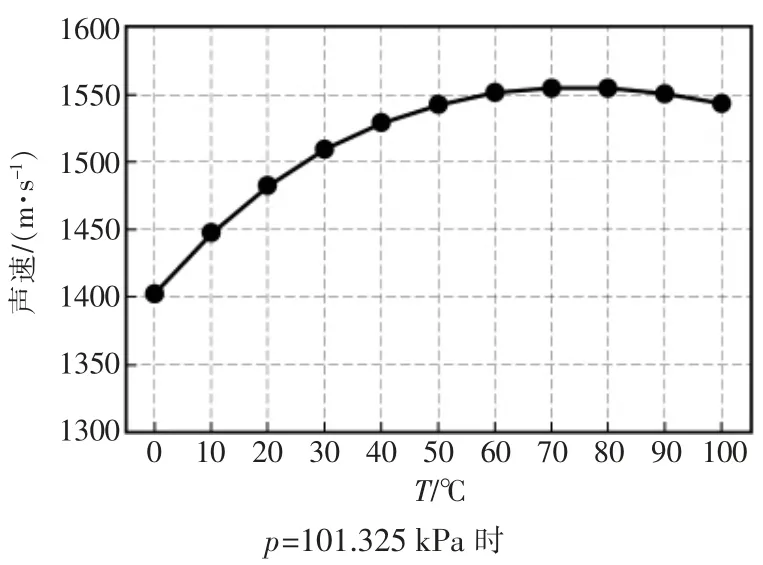
图1 温度与声速的关系Fig.1 Relationship between temperature and sound velocity

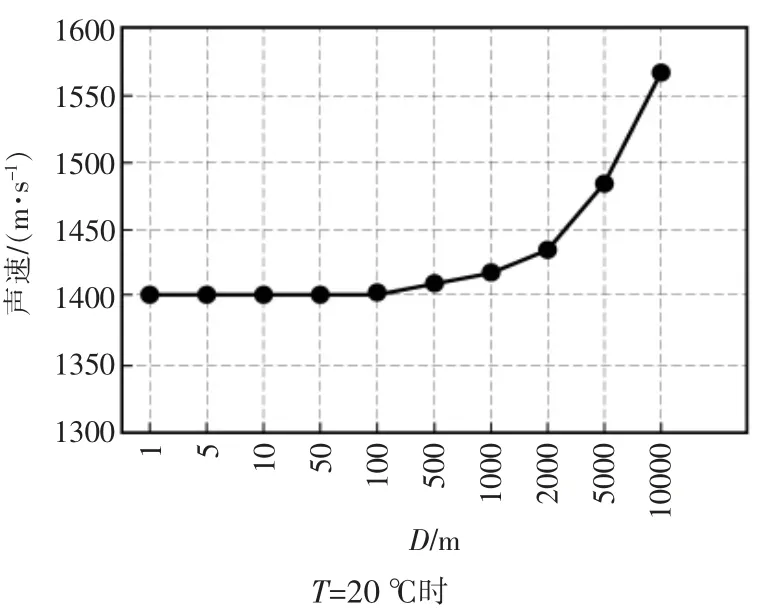
图2 深度与声速的关系Fig.2 Relationship between depth and sound velocity

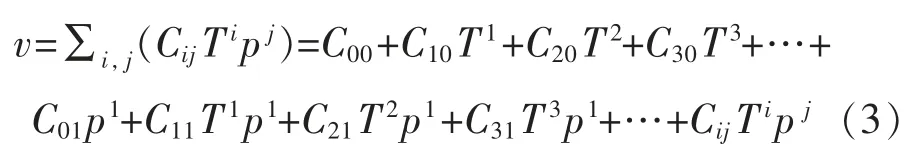
由式（3）计算可得，即使当T分别为0，100 ℃时，T6之后各项所带来的误差均小于0．0001 m/s，可忽略不计。当深度变化较小时，式（3）可简化为

式中：T为温度，℃；p压强，101．325 kPa；v为声速，m/s；C00，C10，C20，C30，…，Cij为非零系数，可根据介质的黏滞性和热传导计算出来，以水为介质所对应的

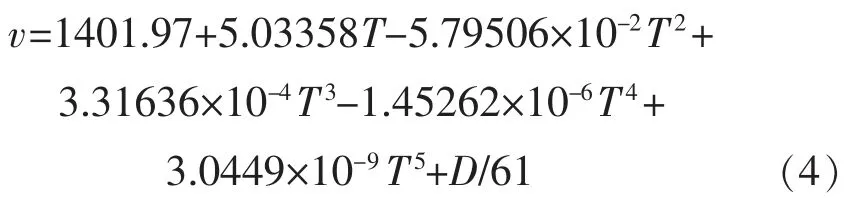
式中：D为水深，m。

多径效应传播路径如图3 所示，除A与D之间的直达波外，测量物的反射波与周围物体（B，C，E）的反射波到达接收端。不同的传播距离使得信号到达接收端的时间有先后。

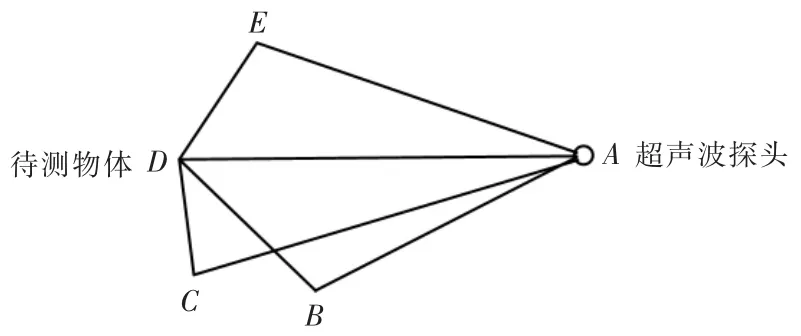
图3 多径效应传播路径示意图Fig.3 Diagrammatic sketch of propagation path of multipath effect

设测距过程中超声波探头与被测物体之间不发生相对位移，超声波发射信号为[5]

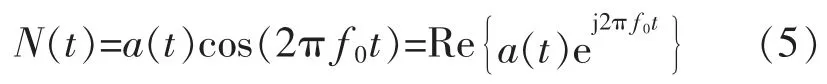
式中：f0为信号频率；a（t）包含了信号幅值。受多径效应影响，接收信号为直射信号与多个路径的传播信号之和，即

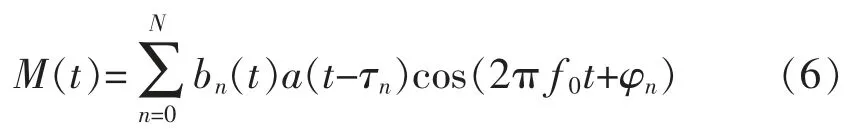
式中：bn（t）为不同路径传播信号幅值的衰减；τn为不同路径的传播信号的时延。

由式（6）可知，多径效应会令接收到的回波信号，在幅值和相位上发生一定程度的改变（衰落和相移）。

若直射信号与多径信号先后到达的时间间隔极短（远小于1 个周期），则二者之间都是在相长叠加，即波谷与波谷之间重叠，波峰与波峰之间重叠。这对于最后的信号接收影响较小。而直射信号与多径信号到达的时间间隔较大时，二者之间可能产生相消叠加，结果会导致信号的失真。然而，多径效应的产生与测量点到待测物体周围障碍物的相对位置分布是密切相关的。

若取信号频率f0＝20 kHz，T＝20 ℃，D＝0 m 条件下，由式（4）可得速度v＝1482．3 m/s。则波长为

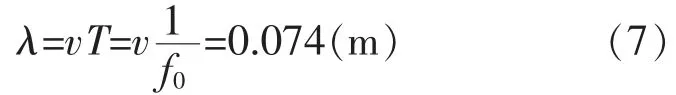
因此，若多径信号传播的路径均比直射信号传播路径多0．074 m（即1 个波长）以上的距离，则接收到回波信号的第1 个周期波形，不会受多径信号的干扰。

以超声波发射点和被测物体作为焦点F1，F2，F1与F2之间的距离为2ce。以F1，F2所在直线为X轴，建立椭圆方程（如图4 所示），即

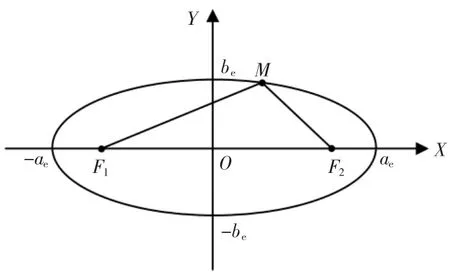
图4 椭圆坐标系Fig.4 Elliptic coordinate system

图中，椭圆上任意一点到F1，F2的距离之和为

其中

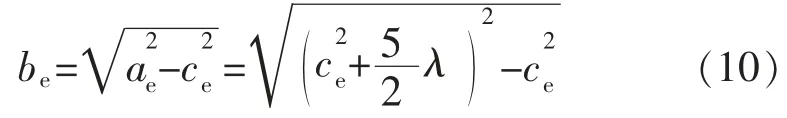
若有一路径信号经过椭圆上某一障碍物M反射后达到的接收端，那么该多径信号传播的距离为2ae+2ce，直射信号传播的距离为4ce。该多径信号比直射信号传播的距离多5λ（即5 个波长）。因此若产生多径效应的障碍物均分布在椭圆之外，那么接收到的回波信号的前5 个周期波形不会受到多径信号的干扰。

2 超声波测距中的误差补偿

不同季节、不同水域的水体温度的变化往往较大。由图1 可见，在p＝101．325 kPa（即水深D＝0 m）时，超声波在0 ℃与20 ℃的水体中波速差值达到了80 m/s。这个差值会造成约5．7%的测量误差，因此获得准确的水体温度对测距的精确度至关重要[6-10]。

由图2 可见，水的深度对波速的影响较不明显。在T＝20 ℃情况下，在深度差值为50 m 的水体中，波速差值也仅为0．8 m/s，造成的误差约为0．057%。在大深度水下环境下的非水平方向上进行测距时，虽然超声波的传播会因经过不同深度的水体导致温度、压力改变，而使波速以一个非线性的关系不断变化，但所带来的误差极小，可以忽略。因此，获得测距点附近的温度和深度作为参数计算波速即可。另外，测量水体的平均深度在50 m 以内时，可视为p＝101．325 kPa 即D＝0 m 情况下计算波速。

由式（7）（9）可知，在波速和测量距离确定的情况下，提高超声波的频率可以缩短波长，缩小椭圆的范围，使椭圆中包围的障碍物数量较少，从而减小多径效应的影响。

若取f0＝50 kHz，T＝20 ℃，D＝0 m 条件下，则速度v＝1482．3 m/s。此时

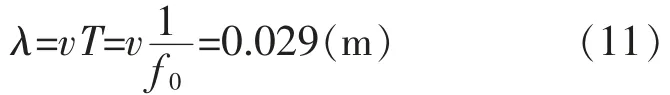
可见，频率越高，超声波传播中的损耗就越大。

另外，在测距过程中适当地调整超声波的发射角度和位置，以改变椭圆的轨迹使包围在椭圆中的障碍物最少，从而减少多径信号对直射信号前5 个周期内的干扰。多径效应所造成回波信号的部分周期波形失真，可以通过增加超声波脉冲的发射个数来加以改善。多径效应所带来的信号衰落，可以通过增大超声波的发射幅值来弥补[11]。

3 试验

试验在水温T＝15．4 ℃，水深D＝0．6 m 的水体中进行。由式（4）可知，超声波在水下的传播速度v为1466．9 m/s。待测物体距超声波换能器4．00 m，超声波频率分别取f0，1＝20 kHz 和f0，2＝50 kHz。由式（7）可得，ce＝4，λ1＝0．073 m，λ2＝0．029 m；由式（8）（10），得到2 个椭圆方程，即

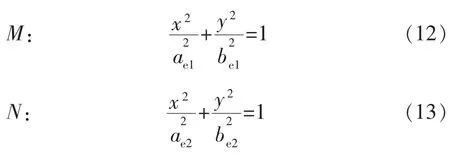
其中

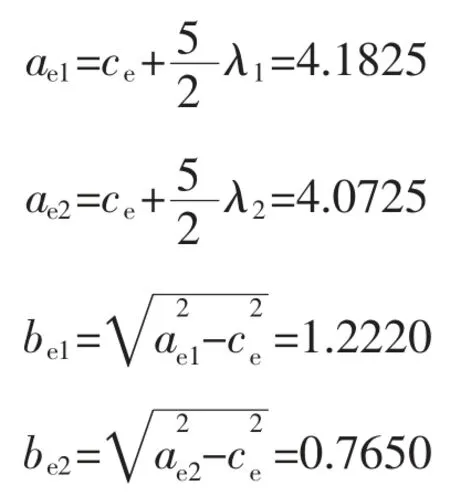
在2 个椭圆之间的阴影区域内布置若干方形塑料板，发射频率首先设置为20 kHz，发出5 个脉冲后停止。调整塑料板位置，直至多径效应的干扰反应在回波波形上，如图5 所示。

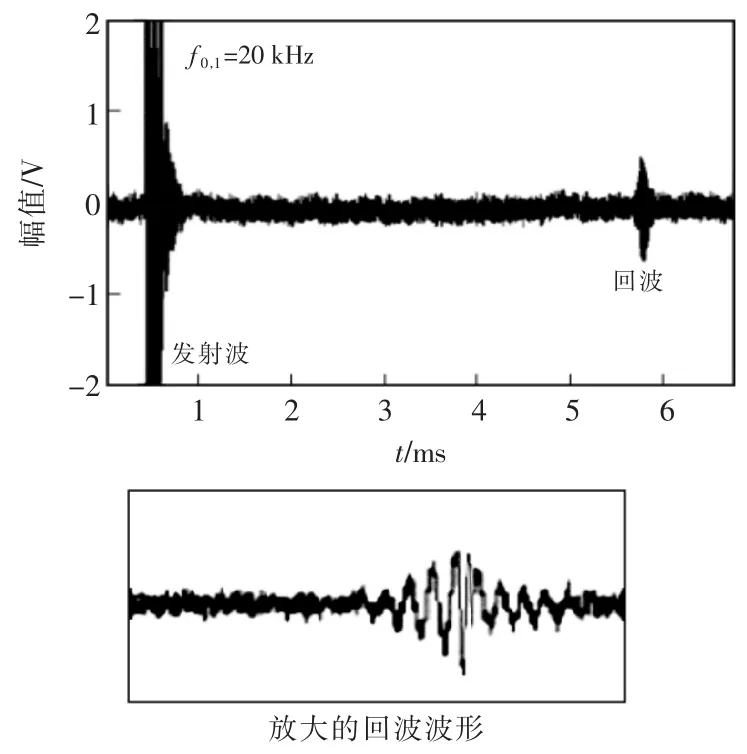
图5 f0，1=20 kHz 时的回波波形Fig.5 Echo waveform at f0，1=20 kHz

保证发射幅值不变，然后提高发射频率至50 kHz，发出10 个脉冲后停止。得到的回波波形如图6 所示。由图可见，回波信号的峰峰值增大，前5 个信号周期波形完整，整体波形失真度降低，更易于被识别。

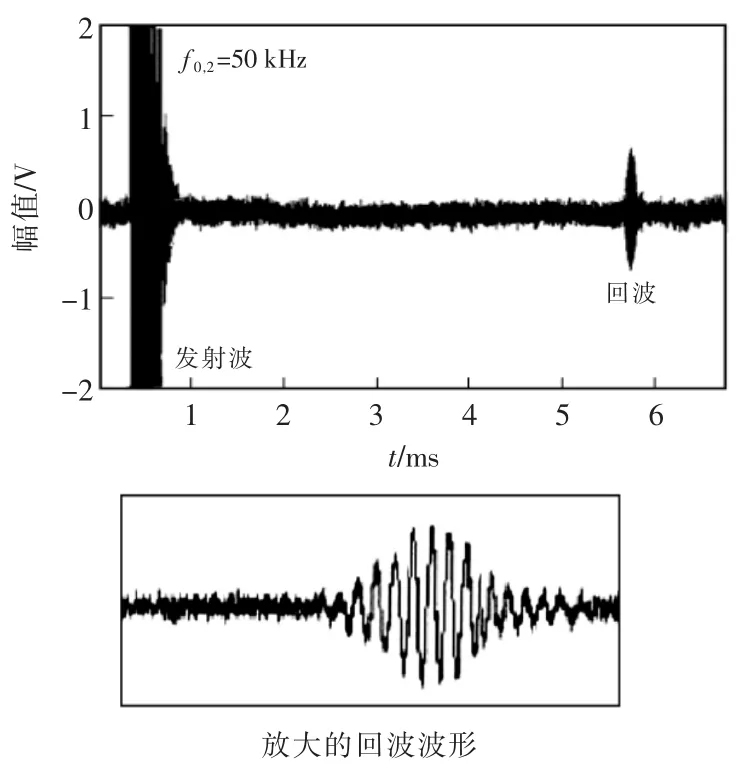
图6 f0，2=50 kHz 时的回波波形Fig.6 Echo waveform at f0，2=50 kHz

4 结语

通过超声波传播过程的建模分析，定量分析了温度、深度和多径效应对测距的影响，获得准确的水体温度对测距的精确度影响较大；水的深度对波速的影响较不明显，超声波在竖直方向上的传播经过的不同深度的水体带来的波速差值可忽略，测量水体的平均深度在5 m 以内时可视为p＝101．325 kPa即水深D＝0 m 情况下计算波速。多径效应的试验验证结果表明，通过增加超声波脉冲发射数量、提高发射频率、调整超声波的发射角度和位置，来改变椭圆的轨迹，可减少多径信号对直射信号的干扰和回波信号的失真，有效改善超声波回波信号识别判断其传播时间，减小测量误差。