一道2013年湖北高考题的不同解法引发的思考
2021-01-11杨雪苹
杨雪苹
(广州大学附属中学南沙实验学校 广东·广州 511458)
0 引言
把问题的数量关系与空间形式结合起来考察,或者把图形的性质转化为数量关系问题,这种处理问题的思想方法就是数形结合的思想方法。在学习和教学中,运用数形结合的思想方法进行解题,可以使得问题处理的更加简单,便捷。一方面,借助于图形的性质可以将许多抽象的数学概念和数量关系形象化、简单化,给人以直觉的启示;另一方面,将图形问题转化为代数问题,以获得精确的结论。
1 高考题引入

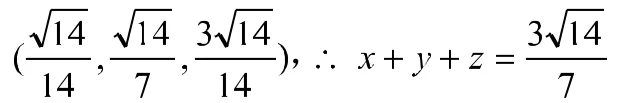
2 数形结合的转换
2.1 由形到数的转换
2.1.1 用向量法进行转换
上题中第二种解法就是数形结合里由形到数的转换中的向量法,题中的式子表示的是空间几何图形,将几何图形向量化,运用向量解决几何中的问题,把抽象的几何推理化为代数运算,特别是空间向量法使解决立体几何中平行、垂直、夹角、距离等问题变得有章可循。
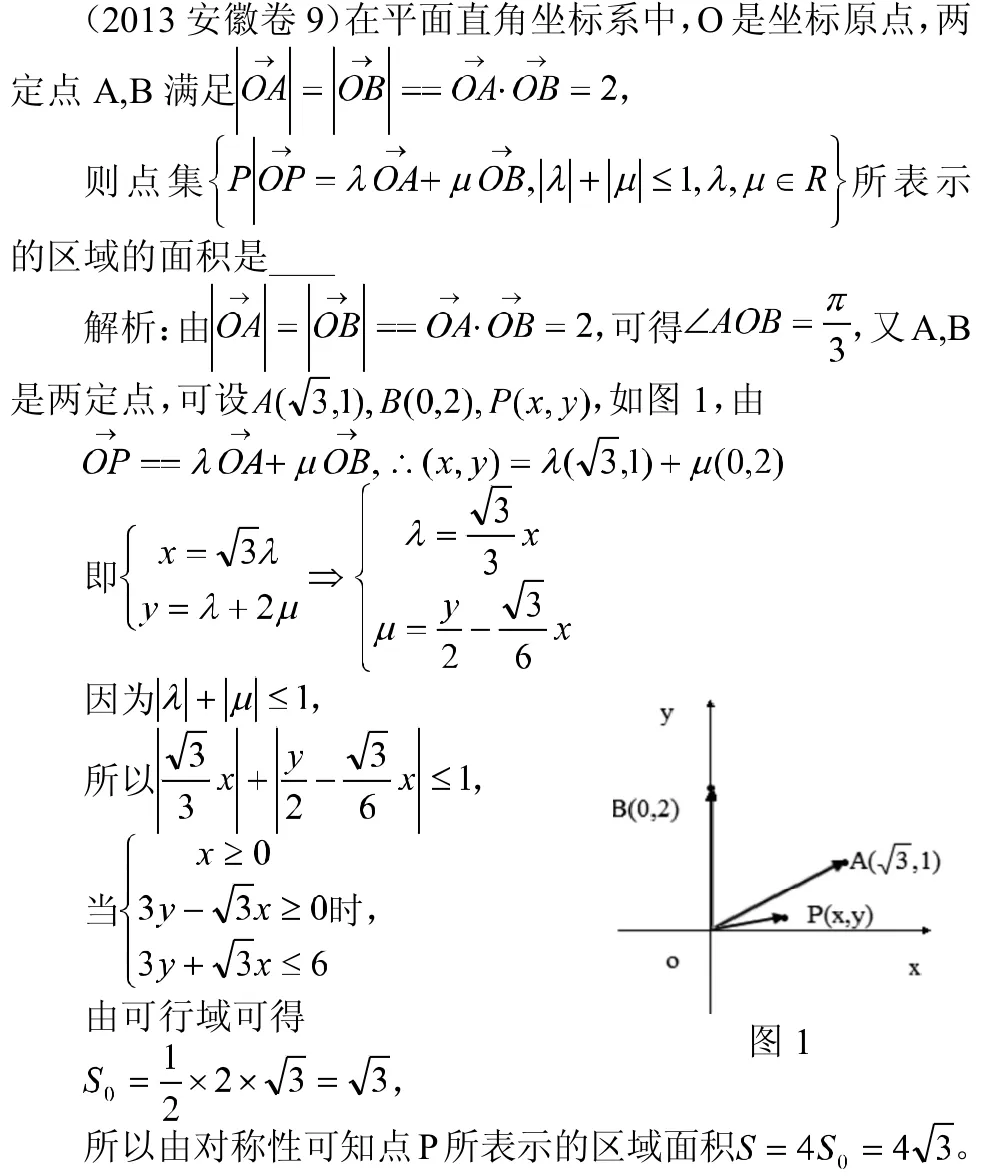
2.1.2 用解析法进行转换
建立适当的坐标系引进坐标将几何图形变换为坐标间的代数关系,把题目进行由形到数的转换,可以使得解题更加简单。
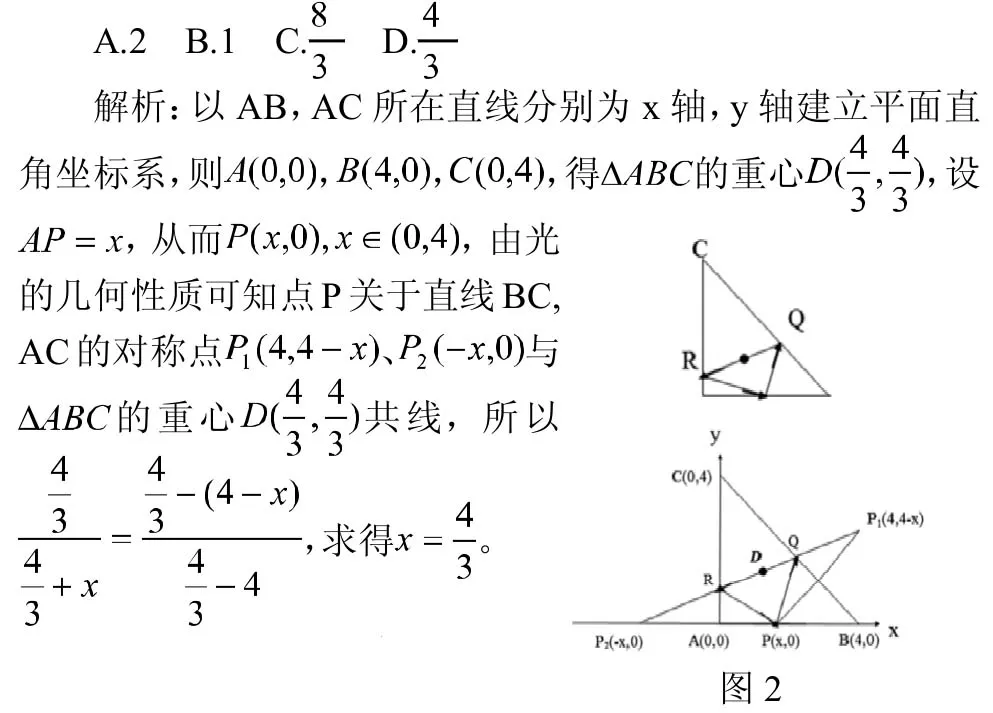
2.2 由数到形的转换
2.2.1 与三角函数结合
利用数形结合解题不仅在高考题中出现,在一些竞赛题目中也常常使用。


该题巧妙地运用了数形结合思想,由不等式的形式构造了图形中两点的距离,由数到形进行转化,使得解题变得简单,在平常的做题中有很多这种数与几何图形结合的题型,比如数形结合求最值,数形结合与函数与方程等等,做题时一定要细心观察,这样才能使得解题得心应手。


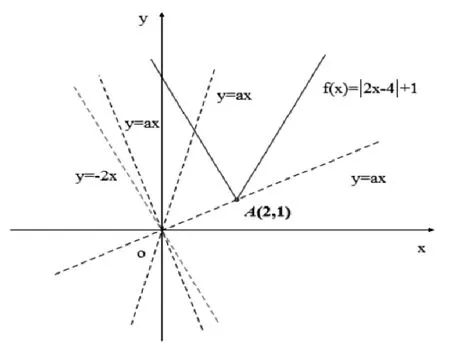
图5
3 数形结合思想运用的建议
数形结合法要求教师在长期的教学过程中潜移默化的让学生掌握,仅仅靠几节课、几道例题,是不能使学生真正理解和掌握数形结合方法的,因此在教学中教师要经常督促学生时刻学会运用数形结合思想解题,在解题过程中要注意以下几点:
第一,要善于观察,在“由形到数”的转换过程中,要注意说明图形的特征、有哪些重要的点(特殊点)、有些什么性质,以及性质的来源等;
第二,要善于运用,在“由数到形”的转换过程中,要巧妙的运用数的特点,构造所需要的图形,结合图形的特殊性,找准关键点所在,巧妙解答;
第三,在利用数学结合思想解题时,不能简单构造图形,定义向量,一定要注意数的取值范围,图形的边界。
4 小结
数形结合有利于提高思维的深刻性,因此,数学教学中,数形结合不应仅仅作为一种解题方法,而应作为一种基本的、重要的数学思想,作为数学知识的精髓,作为将知识转化为能力的“桥”来学习研究和掌握应用。
要将数形结合法运用于解题教学和解题实践作为解题方法的数形结合,实际上包括两方面的内容:一方面对“形”的问题,引入坐标系或寻找其数量关系用向量方法表示,用“数”加以分析,即“由形到数”的转换;另一方面对于数量关系的问题,分析其几何意义,找出其中所反映的“形”之间的关系,借助形的直观来解决。二者都是数形结合,不可偏废。
