基于FFT变换的LFM信号检测方法研究
2021-01-09王传虎邵文建
王传虎,邵文建,居 易
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
线性调频(LFM)信号作为使用最早也最常见的脉压信号,能够使雷达系统取得宽的时宽和带宽,解决作用距离和距离分辨率之间的矛盾,目前被广泛使用于雷达、电子对抗等领域[1-2]。LFM信号是一种频率随时间做线性变化的非平稳信号,相对于单点频脉冲信号,能够给传统电子对抗侦察接收机的检测带来困难。因此,现代电子对抗侦察系统对于线性调频信号的研究非常有意义。
快速傅里叶变换(FFT)具有宽输入带宽、高频率分辨率、大动态范围和多信号并行处理能力,能够实现侦察频带内信号的全概率截获,成为频谱分析最常用的算法。FFT变换的点数直接影响FFT变换的性能。
基于FFT变换算法原理,本文分析了针对LFM脉冲信号的FFT变换的最优点数,为LFM脉冲信号的FFT频谱分析提供了理论指导。
1 单点频脉冲信号FFT变换
假设采样信号序列为x(n),对应N点FFT变换:
(1)
对于单点频脉冲信号,假设信号峰值为A(当信号在脉宽范围外时,A为0),信号频率为f,初始相位为φ,信号表达式为:
x(t)=Acos(2πft+φ)
(2)
假设信号经过模数变换器(ADC)采样,不考虑ADC采样产生的杂散、噪声和量化误差,并假设采样率为S,且满足香农采样定律:S>2f,采样后的信号表达式为:
(3)

(4)
其FFT变换为:
(5)
由于|ejφ|=1,由式(5)可知:
(6)
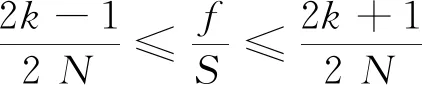
max(|X(k)|)≤AN
(7)


而在实际接收机设计中,由于受信号脉宽限制,FFT变换点数N需要折衷考虑。
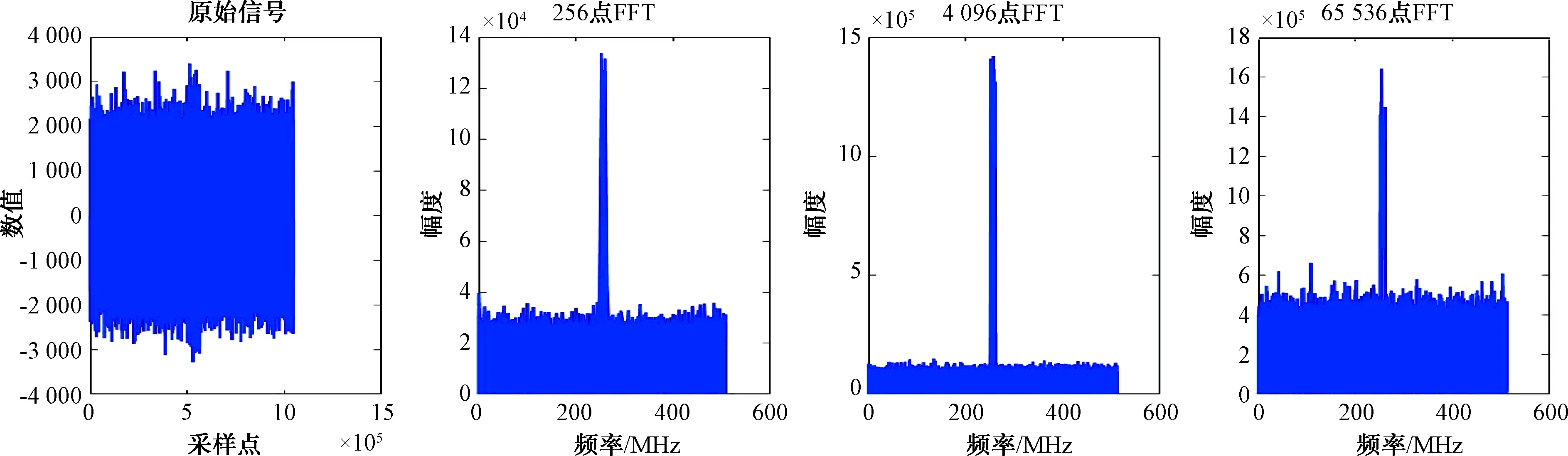
设置仿真信号频率为256 MHz,信号脉宽为50 μs,信号起始时间为500 μs,假设噪声为高斯白噪声,信号信噪比为0 dB与-10 dB,采样率为1 024 MHz,仿真时间为1 024 μs,原始信号以及256点FFT和65 536点FFT变换结果如图1与图2所示。65 536点FFT信噪比增益显著高于256点FFT。在信噪比较低的情况下,65 536点FFT明显优于256点FFT。

图1 单点频脉冲信号FFT仿真(信噪比0 dB)

图2 单点频脉冲信号FFT仿真(信噪比-10 dB)
2 LFM脉冲信号FFT变换
对于LFM脉冲信号,假设信号峰值为A(当信号在脉宽范围外时,A为0),信号起始频率为f,调频斜率为k,初始相位为φ,信号表达式为:
(8)
假设信号经过ADC采样,不考虑ADC采样产生的杂散、噪声和量化误差,假设采样率为S,并假设采样率满足香农采样定律S>2f,采样后的信号表达式为:
(9)
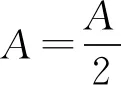
(10)
其FFT为:
(11)
由于|ejφ|=1,由式(11)得:
(12)

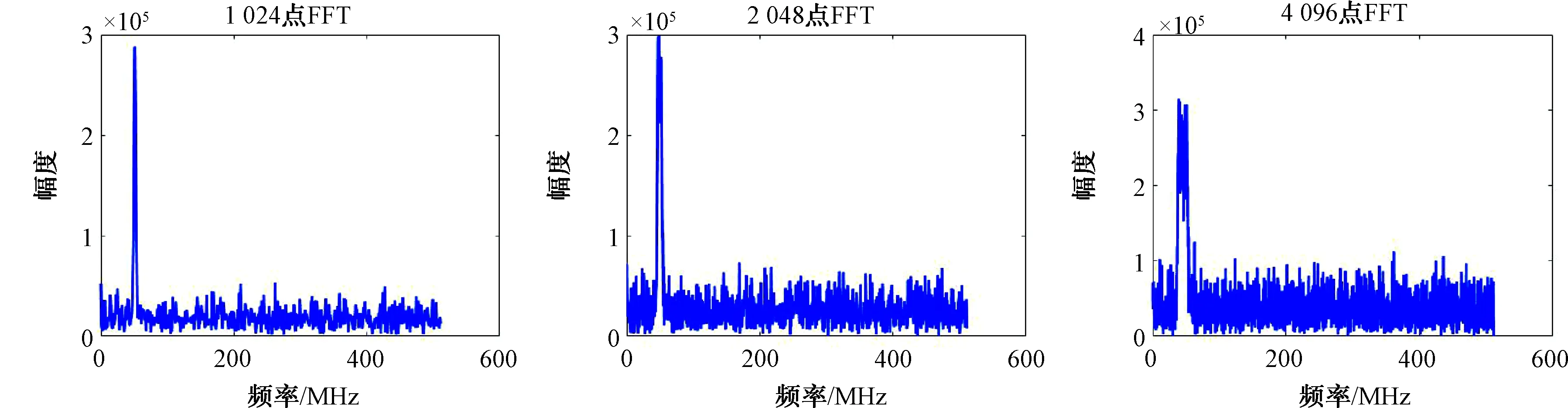
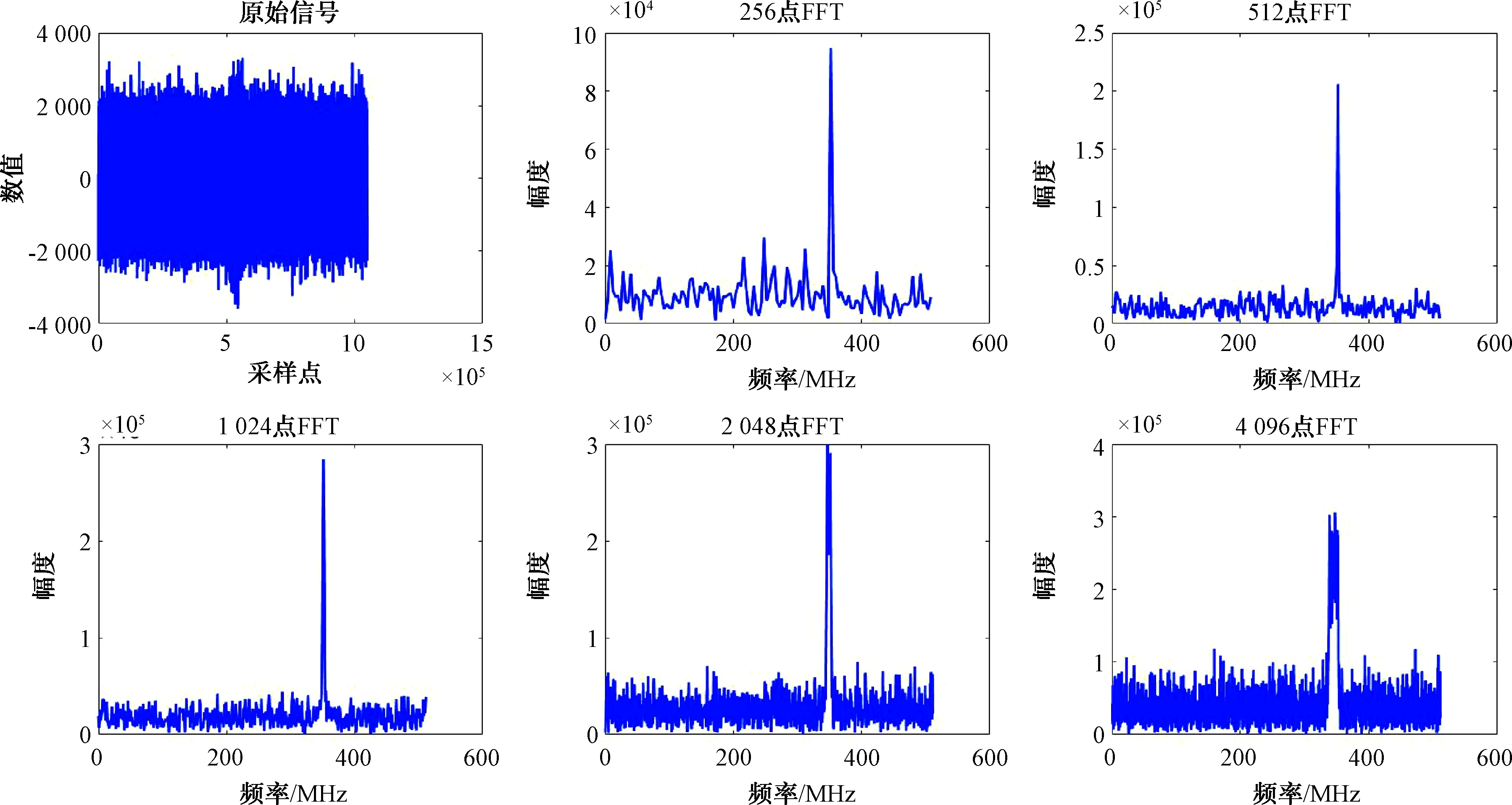
max(|X(k)|) (13) 设置仿真信号中心频率为256 MHz,信号脉宽为50 μs,信号起始时间为500 μs,假设噪声为高斯白噪声,信号信噪比为0 dB,采样率为1 024 MHz,仿真时间为1 024 μs,原始信号以及256点FFT、4 096点FFT和65 536点FFT变换结果如图3以及图4所示。其中图3信号带宽为10 MHz,调频速率为0.2 MHz/μs,图4信号带宽为200 MHz,调频速率为4 MHz/μs。在带宽较窄、调频速率较慢时,4 096点FFT的信噪比增益最优,而带宽较宽,调频速率较快时,256点FFT的信噪比增益最优。而65 536点FFT更多地体现了信号的频谱带宽特性。 如果对信号序列进行滑动FFT,较少点数的FFT同样可以体现带宽特性,如图5以及图6所示。图5信号与图3信号相同,图6信号与图4信号相同。 图3 LFM脉冲信号FFT仿真(调频速率0.2 MHz/μs) 图4 LFM脉冲信号FFT仿真(调频速率4 MHz/μs) 图5 LFM脉冲信号滑动FFT仿真(调频速率0.2 MHz/μs) 图6 LFM脉冲信号滑动FFT仿真(调频速率4 MHz/μs) 图5中4 096点FFT频谱分析特性最优,而图6中,256点FFT频谱分析特性最优,与图3、图4结果相一致。由此可见,点数较少的FFT能够通过滑动的方法反映信号的频谱特性,信号频谱分析的优劣主要取决于FFT处理信噪比增益。 由上节分析,对于LFM脉冲信号,FFT处理增益并不会随着FFT变换点数N的增加而持续增加,因此存在最佳FFT变换点数。而由上节仿真可得,信号带宽和调频速率影响FFT的效果。 假设噪声为高斯白噪声,所有频率幅度相同。由于在FFT变换中,N为2的整幂次,假设FFT变换点数N扩大1倍,则单个点的带宽缩小1倍,即减小3 dB,对于带内信号,FFT变换幅度增益增加6 dB,因此当FFT变换点数N扩大1倍时,噪声功率增加3 dB。 由此,如果FFT变换点数N扩大1倍,对信号增益优于3 dB,则对信噪比增益有改善,否则,会恶化信噪比。 式(10)可以改写为: (14) 对于N点FFT: (15) 由此: (16) (17) (18) 因此: (19) 由之前讨论,2N点FFT相对于N点FFT对信号增益优于3 dB,对信噪比增益有改善。因此最佳FFT点数N应该满足: (20) 结合式(19),得到FFT最优点数N须要满足的条件: (21) 由式(21),FFT最优点数N仅与采样率S以及信号调频速率k有关。 选择仿真信号中心频率分别为105 MHz、256 MHz、405 MHz的信号,信号脉宽为50 μs,信号起始时间为500 μs,假设噪声为高斯白噪声,信号信噪比为0 dB,采样率S为1 024 MHz,仿真时间为1 024 μs。 选择与图3相同的信号,信号带宽为10 MHz,调频速率k为0.2 MHz/μs。由于在FFT变换中,N为2的整幂次,仅有2 048和4 096满足式(21),因此最优的FFT点数N为2 048或者4 096。原始信号以及相应点数FFT变换结果如图7、图8、图9所示。 由图7、图8、图9,最优的FFT点数为4 096,满足式(21)估计。 选择与图4相同的信号,信号带宽为200 MHz,调频速率k为4 MHz/μs。由于在FFT变换中,N为2的整幂次,仅有512和1 024满足式(21),因此最优的FFT点数N为512或者1 024。原始信号以及相应点数FFT变换结果如图10、图11、图12所示。 由图10、图11、图12,最优的FFT点数为1 024,满足式(21)估计。 图7 LFM脉冲信号FFT仿真(信号中心频率105 MHz,调频速率0.2 MHz/μs) 图8 LFM脉冲信号FFT仿真(信号中心频率256 MHz,调频速率0.2 MHz/μs) 图9 LFM脉冲信号FFT仿真(信号中心频率405 MHz,调频速率0.2 MHz/μs) 本文基于FFT变换算法原理,分析了FFT变换的点数对LFM脉冲信号频谱分析的影响,并推导了对于特定LFM脉冲信号,FFT变换的最优点数需要满足的条件。该条件仅与采样率以及信号调频速率有关。本文随后仿真验证了该条件。本文为LFM脉冲信号的FFT频谱分析提供了理论指导。 图10 LFM脉冲信号FFT仿真(信号中心频率105 MHz,调频速率4 MHz/μs) 图11 LFM脉冲信号FFT仿真(信号中心频率256 MHz,调频速率4 MHz/μs) 图12 LFM脉冲信号FFT仿真(信号中心频率405 MHz,调频速率4 MHz/μs)



3 LFM脉冲信号FFT变换最优点数的研究


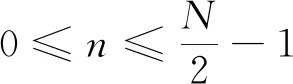
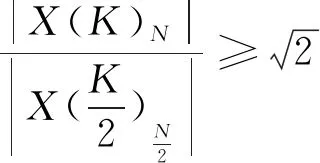
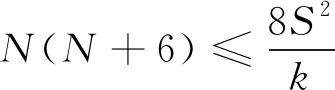
4 仿真实验



5 结束语