一种基于期望最大化的多目标轨迹拟合算法
2021-01-09盛骥松
刘 禹,李 培,盛骥松
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
在现代和未来战争中,随着战争空间日益复杂化、目标环境多样化,为了更准确地获得打击目标,需要借助侦测信息对目标轨迹进行拟合。传感器采集到的测量值,由于受到环境中噪声等因素的影响,使得测量值存在一定的误差,且现代雷达信号样式繁杂,侦察设备难以精准捕获同一批次的完备信息,且同一目标容易出现多批次问题,利用批次对目标进行轨迹拟合,容易造成轨迹分段、轨迹信息缺失等问题。鉴于此,本文提出一种宏观进行轨迹拟合的思路。本文将轨迹拟合拆分为2个主要阶段,即:轨迹个数估计和轨迹拟合。本文将轨迹个数作为先验知识,重点研究轨迹拟合问题。
传统轨迹拟合可分为3个类型:(1)现代智能类算法;(2)参数估计算法;(3)统计方法[1]。本文提出基于期望最大化(EM)的多目标轨迹拟合算法,在传统EM统计的基础上进行理论迁移,实现多轨迹融合算法。本文主要分为4个部分:(1)对EM算法进行介绍;(2)论述本文思路以及创新点;(3)针对不同算法进行仿真分析;(4)全文总结。
1 EM算法
EM算法[2-6]解决的问题可表述为:给定输入——观测变量数据Y,隐变量数据Z联合分布P(Y,Z|θ),条件分布P(Z|Y,θ);估计输出——模型参数θ。对于输入模型,利用最大似然准则,可建立目标函数:
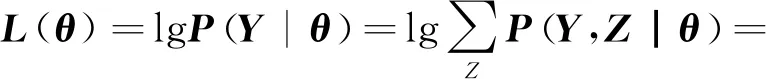
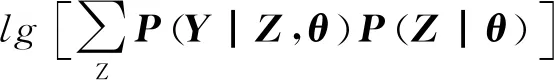
(1)
对于上述优化问题,若观测变量完备,则准则函数L(θ)可借助最大似然估计(MLE)准则求解。但由于隐变量Z的存在,准则函数没有闭式解,一种思路是将P(Z|θ)看作已知,进一步求解参数θ,如此反复迭代,最终完成求解。但如此求解存在2点不足:(1)MLE求解过程中,存在分子分母求和、积分项,反复迭代增加运算复杂度;(2)不能确保该迭代操作满足收敛条件。为了解决这两点不足,A.P.Dempster提出了EM算法。首先,考虑第i次迭代后的准则函数不小于原始准则函数,根据JENSEN不等式:
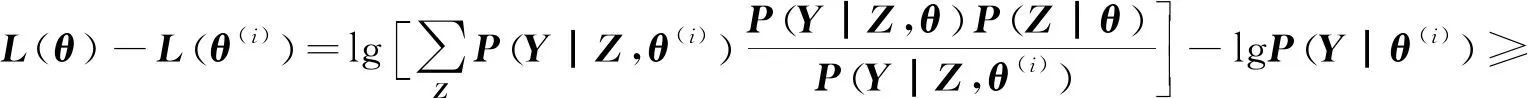
(2)
省去对θ(i)的极大值而言是常数的项,由上式进一步得出:
θ(i+1)=
(3)
EM算法具体步骤如下:
步骤1:选择参数的初始值θ(0),开始迭代;
步骤2:E步(求Q(θ,θ(i))):记θ(i)为第i次迭代参数θ的估值,在第i+1次迭代的E步,计算:
Q(θ,θ(i))=EZ[lgP(Y,Z|θ)|Y,θ(i)]=
(4)
式中:P(Z|Y,θ(i))P(Z|Y,θ(i))是给定观测数据Y和当前参数估计θ(i)下隐变量Z的条件概率分布。
步骤3:M步(在隐变量条件概率密度给定的前提下,利用MLE实现参数估计)求使Q(θ,θ(i))最大化的θ,确定第i+1次迭代的参数的估计值θ(i+1):
(5)
步骤4:重复步骤2、3,直到满足收敛条件。
至此,完成了EM算法的整个推导过程。
2 多轨迹拟合算法
2.1 混合高斯模型
根据上文推导,对于混合高斯模型(GMM),只要求解P(Zj∈Yk|Yj,Θ(i))即可。其中Zj∈Yk表示第j个观测点来自第k个模型,Θ表示参数的集合。对于K个混合高斯模型,利用全概率公式,容易得到:
(6)
进一步写出准则函数:
(7)
式中:θk=[μk,σk],为分布k对应的参数;Θ={θ1,θ2,…,θK},为参数集合;N为样本个数。
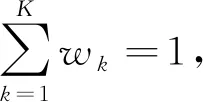
(8)
偏微分求解:
(9)
得:
(10)
对各分布内部参数θk进行优化,给出准则函数:
(11)
对于高斯分布:
(12)
对参数求偏导:
(13)
(14)
至此完成了混合高斯模型的整个求解。
2.2 混合拉普拉斯模型
不同混合模型,参数形式不同,高斯模型因为是偶次幂而易于求解,对于奇次幂求导存在符号函数,难以直接求导迭代,因此解决奇次幂求解的问题,将进一步提升混合模型的普适性(不局限于高斯模型、拉普拉斯模型)。对于拉普拉斯分布:
(15)
式中:μ为均值;b为陡峭系数。
对于K个模型的混合分布:
(16)
E步骤与混合高斯模型求解相同,对于任意混合模型均适用。M步骤里系数的求解操作同样适用各种模型,对于陡峭系数b求解:
(17)
对均值求解:
(18)
此时无法完成迭代求解,换个角度,在迭代的最终状态,可以认为i次参数与i+1次参数近似相等[8],从而上面的求导结果转化为:
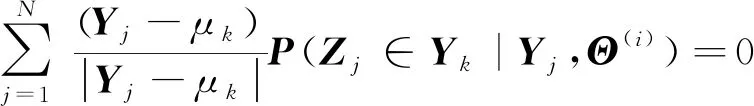
(19)
从而完成均值的迭代:
(20)
至此完成奇次幂混合模型的参数求解。
2.3 混合线性模型
讨论不同的分布,主要是考虑传感器接收到的雷达信号存在的噪声特性不同。上文已解决了大部分随机平稳噪声场景的参数求解,不失一般性,假设传感器接收到信号的噪声为高斯噪声。下面论述如何从基于EM的混合分布模型迁移到轨迹拟合算法。
对于单条轨迹,可以借助最大似然(MLE)等算法进行轨迹拟合,但对于多条轨迹,该算法难以直接应用。假设一堆数据点(xj,lj),由2条直线轨迹产生:
(21)
式中:n1j、n2j分别为对应的随机噪声。
虽然无法直接利用MLE求参,但不同轨迹的噪声,可以看作是混合模型的应用,对应到这里就是混合高斯模型:
(22)
可以认为lj-akxj就是GMM中的Yj,bk就是μk。直接套用GMM中的迭代结果:
(23)
(24)
所不同的是,多了一个对ak的求解,容易得出:
(25)
至此,理论推导完成。
上文以线性轨迹举例,推导了线性多轨迹拟合的可行性。更一般地,噪声模型可由高斯模型推广至其他多种混合模型;对于线性轨迹,同样可以推理到多种类型的轨迹模型。更一般地:
(26)
g为一般表达式,如GMM就是g=ax+b,更一般的g理论上可以为任意表达式,如图1。
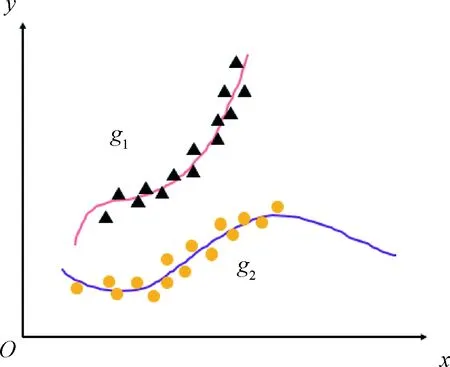
图1 轨迹拟合示意图
只要将g的具体表达式代入EM求解过程即可。事实上,混合模型理论上可以实现各类形状的聚类,而噪声同样可以基于不同的分布假设:(1)常见的K-means本质是对于中心点(聚类中心)的分布假设;(2)高斯混合模型是对于斜率为0的直线(GMM的均值)的分布假设;(3)各种轨迹的拟合是EM算法的一般应用。
3 仿真试验
仿真环境:假设2批目标在不同的线性轨迹上,且由于作用距离不同,2个轨迹的参数误差不同,仿真基于式(26)所描述的轨迹模型,目标数量K取2;噪声为y(i)=0.5×x(i)-3+100×R和y(i)=-7×x(i)+2+50×R,是高斯白噪声,其中R为随机数。
利用本文提出的多轨迹拟合算法,仿真结果如图2所示。
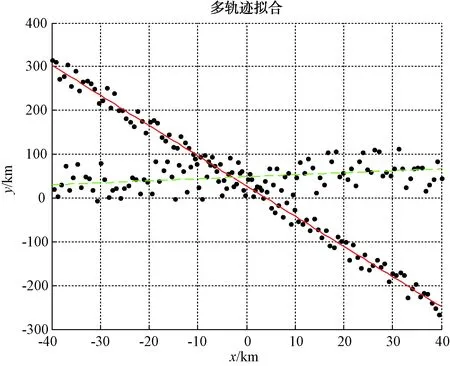
图2 轨迹拟合结果
从图2中可以看出,本文提出的多轨迹拟合算法很好地拟合出了轨迹,仿真结果验证了本文算法的有效性。
4 结束语
本文作为多轨迹融合算法的新的尝试,跳出传统单批次信息不足、多批次可能对应同一目标等局限性,从宏观上论述了轨迹拟合理论的可行性,并进行仿真验证。该算法可以作为传统轨迹拟合的辅助信息,在整体上寻找轨迹将有利于目标参数的进一步深度融合。本文提出的轨迹拟合算法在应用层面、理论层面都存在一定的不足,但作为该方向的一个初步的探索,解决了部分理论难题,并梳理出初步的理论架构,仍然具有重要的借鉴意义。
