以“基本事实4”为源头的平行关系教学

郑新春　张梅

摘  要：以基本事实4为源头，以展示基本事实4的一个简易图形助力平行关系的单元教学，营造了源水不断、清澈见底的教学意境，促进了学生对知识的结构性理解.

关键词：基本事实4;源头;平行关系

在平行关系的学习过程中，人们一般认可从线线平行到线面平行再到面面平行的逻辑关系. 但是对基本事实4（直线平行的传递性）之于平行关系的奠基地位却少有提及. 笔者在设计平行关系单元教学的活动中，经过一番研究，有了一些心得，故不揣浅陋，成就此文，以期得到同行的指正.

一、基本事实4堪为源头

众所周知，基本事实4是直线平行的传递性定理，而非公理，是在欧几里得《几何原本》的第11卷作为命题9给出的，陈述为“两条直线平行于和它们不共面的同一直线时，这两条直线平行”. 关于它的证明，有学者做了详实的研究，但这些证明大多繁难（详见参考文献）. 有的教师借助“线面平行的判定或性质”推得“直线平行的传递性”，即使不犯循环论证的错误，也有悖于教材先研究线线关系再研究线面关系的呈现顺序. 因此，教材的编写，秉持能力训练要循序渐进的理念，规避难点，把直线平行的传递性定理长期当作基本事实（公理）来处理，这样做符合高一学生的逻辑推理能力实际，深受师生欢迎.

笔者在人教A版《普通高中教科书·数学》（以下统称“教材”）必修第二册“直线、平面平行关系”的备课中，突然萌生一种想法，按照教材顺序，运用基本事实4之前的知识，是否存在学生可接受的基本事实4的证明呢？若存在，学生获取的知识结构将更具逻辑性. 于是，根据基本事实1、基本事实2和基本事实3确定平面和直线的重要思想，笔者经过一番思考，偶得证明，心结释然.

题目  已知直线[a，b，c]，[a∥b，b∥c]. 求证：[a∥c].

证明：先证直线[a，c]共面.

因为[a∥b]，[b∥c]，

所以直线[a]与直线[b]确定一个平面，设为平面α，直线[b]与直线[c]确定一个平面，设为平面β. 如图1所示.

不妨取直线[c]上一点[P∉a]，

故直线[a]与点[P]可以确定平面[γ].

所以[P∈γ]，[a⊂γ].

由[c⊂β]，得[P∈β].

所以平面[β]与平面[γ]有一条过点[P]的公共直线[c].

所以[b⊂β，c⊂β，c⊂β，c⊂γ].

若直线[c]与直线[c]相交，由[b∥c]，得直线[b]与直线[c]相交（否则与平行公理矛盾）.

设[b⋂c=Q]，则[Q∈b⊂α，Q∈c⊂γ].

据基本事实3，[Q∈a]，与[a∥b]矛盾.

所以直线[c]与直线[c]重合，即[c⊂γ].

所以直线[a]和直线[c]共面于平面[γ].

再证[a∥c].

若直线[a]与直线[c]相交，

则其交点在平面[α，β]上.

于是其交点在直线[b]上，即[a，b，c]三线共点.

这与直线[a，b]平行矛盾，即得[a∥b，b∥c.]⇒a∥c

上述证明，主要用到“确定平面的条件”“两平面若有公共点，则存在唯一一条公共直线，且公共点在公共直线上”，这些知识属于基本事实4之前的知识. 因此，此证明为基本事实4作为后续知识的源头奠定了坚实的逻辑基础.

行文至此，可能引发同行的质疑，因为在教材中，“常用逻辑用语”一节删去了“四种命题”，尤其是“逆否命题”，这样就出现了一个不可回避的问题，即使我们失去了论证“反证法”合理性的逻辑机理. 因此，上述内容是否有不合时宜之嫌？事实上，笔者并无让学生掌握反证法证明之意，作为教师，能证明基本事实4，不妨视为登高望远之举. 至于在教学中，一方面，我们要理解教材编写删繁就简、突出知识主干、能力训练循序渐进的意图;另一方面，根据学生的实际基础，适当渗透反证法“若矛盾，则不可能”的思维方式. 这完全可以立足于高一学生在生活中的说理经验，说明道理即可，而不必要求学生严格按照反证法的格式书写证明. 下文的教学过程中，我们就是这样来处理相关内容的，相信这样做，对提升学生的直观想象、逻辑推理素养，以及以理服人的行事原则，一定大有裨益.

二、教學中一个模型“包打天下”

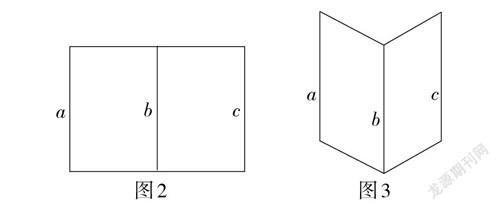
树立了基本事实4的奠基地位后，我们不难想到一个教学模型，如图2所示. 即在一张矩形纸片上画三条平行线段[a，b，c]（亦可降低难度，让学生直接将矩形纸片对折得[a，b，c]），然后以线段[b]为折痕，观察图3的折叠过程，并讨论线段[a，c]是否平行.

没想到的是，如此简单的一个模型，在直观化、符号化后，竟在线线平行、线面平行、面面平行的教学中，一贯到底、“包打天下”，为以基本事实4为源头的教学增色添彩.

1. 基本事实4

基于前文的论述，我们对基本事实4的教学，就有了两种合理的选择.

其一，如果学生基础一般，教学就从折叠矩形纸片开始，学生通过观察如图2和图3所示的模型，先承认直线[a，b，c]在同一个平面内，两条直线[a，c]平行毫无悬念，然后通过操作确认，在折叠过程中[a∥c]始终成立. 于是，得到基本事实4，提炼出平行的传递性.

其二，如果学生基础好，就可以进一步讨论折叠过程中[a∥c]是否始终成立. 考虑到学生独立完成证明会有困难，教师可以仿照图1提示学生，先研究直线[a，c]是否共面. 若不共面，经过怎样的思考可以推出矛盾？于是，说明一定共面. 判断直线[a，c]共面后，再研究直线[a，c]是否相交. 若相交怎么样？能否推出矛盾？进一步说明直线[a，c]不可能相交，得[a∥c]，即平行的传递性定理.

2. 等角定理

教材中等角定理的表述为：如果空间中两个角的两条边分别对应平行，那么这两个角相等或互补. 若再粗放一些，不计较角的方向，可以把等角定理表述为“两条直线平移不变成角”. 这样认识问题很重要，因为它揭示了确定或计算空间任意两条直线（异面直线）所成角的通则. 而在基本事实4中，人们先关注的是“若[a∥b，b∥c]，则[a∥c]”，即平行的传递性. 其实，换一个角度，我们不妨视直线[b]为两条直线[b，b]的重合，视直线[a，c]分别是直线[b]与直线[b]的平移，那么，基本事实4的实质依然是“两条直线平移不变成角”，只不过成角为[0°]罢了.

由此可见，对于基本事实4的源头地位，等角定理并没有多大干扰，它与基本事实4出如一辙，都是在两条直线平移的条件下，成角为[0°]或任意角相等的两种形式而已.

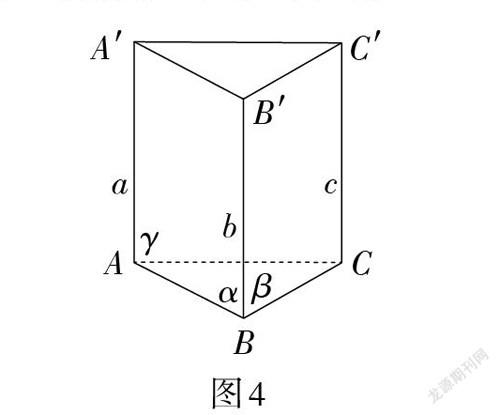
在课堂教学中，以基本事实4为基础，在三条平行线[a，b，c]上，分别截取等长的线段[AA，BB，CC]，然后以[b]为折痕，连接[AB，BC，AC，AB，BC，AC]，得到图4，让学生完成如下学习任务.

（1）观察图4，找出除[a，b，c]之外的平行直线对，并给出证明.

（2）找出相等的角，并给出证明.

（3）进一步分析造成[∠ABC=∠ABC]的原因，判断是因为[a∥b，b∥c]，还是因为折叠前后始终都有[AB∥AB]和[BC∥BC]呢. 进而概括出等角定理.

（4）观察基本事实4与等角定理，试研究两者之间的内在联系，得出“两条直线平移不变成角”的共性结论.

如果学生基础好，当然也可以让学生从“平移不变成角”的角度去理解基本事实4，然后提问：图4中还有哪些直线（线段）是平移关系？它们是否符合“平移不变成角”？进一步概括等角定理.

3. 线面平行

（1）寻找线面平行的判定方法.

在基本事实4的前提下，观察图4，想象随着折角的变化，直线[b]与直线[a，c]所确定的平面[γ]的相对位置也发生变化. 依此背景，让学生思考如下两个问题：观察，直线[b]与平面[γ]可能的位置关系有哪些？若排除直线[b]在平面[γ]内的情况，能否得线面平行的判断方法？

对于第一個问题，我们可以得到直线[b]与平面[γ]可能的位置，只有[b⊂γ]或[b∥γ]，不可能有直线[b]与平面[γ]相交（若直线[b]与平面[γ]相交，则易知直线[b]与直线[a]相交，或直线[b]与直线[c]相交，这与题设矛盾）.

对于第二个问题，我们可以得到如下猜想：平面外一条直线若平行于平面内的两条平行直线，则该直线与平面平行. 此时，教师可以引导学生质疑：需要两条直线吗？平面外的一条直线若平行于平面内的一条直线，据基本事实4，即有平面外的一条直线必然平行于该平面内的一簇平行直线，所以无需两条直线. 由此可以得到线面平行的判定定理：如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行.

虽然教材中对此定理不要求严格证明，但是如前所述，我们可以引导学生这样思考问题：如果直线[b]与直线[a，c]确定的平面不平行，就必然相交，则交点要么在直线[b，a]确定的平面上（直线[b，a]相交），要么在直线[b，c]确定的平面上（直线[b，c]相交）. 无论哪种情况，都可以推出与直线[b，a]平行矛盾，或与直线[b，c]平行矛盾，所以直线[b]与直线[a，c]确定的平面相交是不可能的. 于是只剩下平行这种情况.

（2）探究线面平行的性质.

若已知直线[b]平行于平面[γ]，我们可以得到什么性质？这个问题提出后，教师可以引导学生继续观察图4，探究在直线[b]与平面[γ]平行的条件下，我们可以得到哪些结论.

从线面平行的定义上看，直线[b]与平面[γ]没有公共点，这说明平面[γ]内的所有点都不在直线[b]上，平面[γ]内的所有直线都与直线[b]没有公共点，即平面[γ]内的所有直线与直线[b]要么平行，要么异面. 我们如果知道了平面[γ]内的哪些直线与直线[b]平行，那么平面[γ]内的剩余的那些直线就与直线[b]异面.

我们现在要研究的问题是：在平面[γ]内，如何确定与直线[b]平行的直线？

进一步观察图4，我们已知平面[γ]内的直线[a，c]与直线[b]平行，联想到直线[a，c]分别是平面[γ]与平面[α]和平面[β]的交线，自然想到过直线[b]上的平面任意旋转，与平面[γ]的交线都与直线[a，c]平行，也与直线[b]平行，我们把这番操作概括为“搭平面、得交线，交线与直线[b]平行”. 于是，得出直线与平面平行的性质定理：一条直线与一个平面平行，如果过该直线的平面与此平面相交，那么该直线与交线平行.

在前面分析的基础上，该定理的证明是显然的. 因为直线[b]平行于平面[γ]，所以直线[b]与平面[γ]无公共点，而“搭平面、得交线”后，显然直线[b]与交线共面且无公共点，于是，直线[b]与交线平行.

4. 面面平行

（1）寻找面面平行的判定方法.

教学中，可以引导学生观察图4，想象折纸的过程中，直线[a，c]依然平行，自然得到三棱柱的直观印象，再结合棱柱的定义，不难发现平面[ABC]与平面[ABC]平行. 这时，教师要引导学生思考：这两个平面平行是由[a∥b，b∥c]引起的，还是由折叠前后始终都有[AB∥][AB]和[BC∥BC]引起的呢？一般来说，学生能发现后者是引起平面[ABC]与平面[ABC]平行的根本原因. 将这个直观感知的事实用文字进行描述，即得“如果一个平面内的两条相交直线分别与另一个平面内的两条相交直线平行，那么这两个平面平行”. 接下来，我们结合前面线面平行的判定定理的讨论，得到与上述描述等价的命题，即面面平行的判定定理：如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行.

至于该定理的证明：一方面，我们可以采用教材的处理方式，从长方体模型出发，遵循“直观感知，操作确认”的理念，不在定理证明处做文章，只在定理的获得和运用方面进行强化;另一方面，考虑到该定理的证明既是对直线与平面平行的性质定理的一次很好的应用，又可以满足学生对逻辑思维能力发展的需求. 在学生基础比较好的情况下，我们依然可以采用前文所述“线面平行判定定理”的处理方式，即假如由相交直线[AB，BC]确定的平面与平面[ABC]不平行，就必然相交，得交线[d]，依据线面平行的性质定理，必有相交直线[AB，BC]同时与直线[d]平行，这显然是“不可能”的，即得面面平行的判定定理. 而如果把题设中的“相交直线[AB，BC]”“平行直线[AB，BC]”这种“不可能”就变为“可能”，那么平行直线[AB，BC]确定的平面与平面[ABC]不平行，也变为“可能”. 于是，题设中直线[AB，BC]由相交变为平行，也即失去了判定面面平行的“资格”.

（2）探究面面平行的性质.

由于两个平面互相平行，那么這两个平面就一定没有公共点，可以据此让学生观察图4，看看能有什么发现？一般而言，学生经过研讨，发现下面两个结论，是可能的：一个平面内的任意一条直线都与另一个平面平行;一个平面内的任意一条直线与另一个平面内的任意一条直线平行或异面.

对于第一个结论，根据平面与平面平行的定义，显然不证自明.

对于第二个结论，我们自然会更关注两条直线相互平行的情况. 引导学生观察图4，不难发现[AB∥AB]和[BC∥BC]. 由此受到启发，要得到两条平行直线，我们可以搭建一个与已知两个平行平面相交的平面，得两条交线. 显然，这两条交线平行是不证自明的事实. 于是，得到面面平行的性质定理.

三、结束语

“问渠那得清如许？为有源头活水来”出自南宋诗人朱熹的《观书有感》，意指水之清澈，缘于源头活水不断注入. 借古喻今，反观平行关系的单元教学，以基本事实4为源头，以展示基本事实4的一个简易模型助力始终，使学生沿一个不变的背景，一贯到底、持续思考、解决问题，形成了源水不断、清澈见底的教学意境，这对促进学生对知识的结构性理解是不言而喻的. 当然，一个知识体系的落实，除问题驱动学生沿一个背景思考外，还需要穿插必要的例题与练习. 限于篇幅，不再赘述.

参考文献：

[1]沈中宇，汪晓勤. 西方早期立体几何教科书中空间平行线的传递性定理[J]. 中国数学教育（高中版），2016（12）：60-64.

收稿日期：2021-07-10

作者简介：郑新春（1971— ），男，中学高级教师，主要从事中学数学教学研究.