印度洋区域地震海啸数值预报系统的建立

王宗辰，史健宇，原野

（国家海洋环境预报中心（自然资源部海啸预警中心）自然资源部海洋灾害预报技术重点实验室，北京100081）

1 引言

2017 年6 月20 日，中华人民共和国国家发展和改革委员会与原国家海洋局联合发布了《“一带一路”建设海上合作设想》，勾勒出3条蓝色经济通道，其中1 条便是：以中国沿海经济带为支撑，连接中国-中南半岛经济走廊，经南海向西进入印度洋，衔接中巴、孟中印缅经济走廊，直至非洲的“海上丝绸之路”。

从地质构造的角度来看，海上丝绸之路依次经过了欧亚板块、印度洋板块和非洲板块。板块交界处常伴有较高的地震活动性，因此也是海啸频发之地。统计显示，自1604年以来该区域发生海啸事件117 次[1]，其中南中国海及周边海域79 次、印度洋区域38次（见图1）。

苏门答腊俯冲带位于印度洋-澳大利亚板块与巽他次级板块的交汇部位，印度洋-澳大利亚板块在这里向巽他次级板块下面俯冲，是世界上最活跃的板块构造边缘。自2004年以来，该区域Mw8.0级以上地震引发的海啸事件达到7 次，8.6 级以上地震海啸3 次，其中最严重的2004 年苏门答腊岛Mw9.2 级地震海啸共造成24～28万人伤亡和失踪，以及十亿美元数量级的经济损失，成为有记录以来死亡人数最多的自然灾害之一[2-4]。海啸的破坏形式不仅包括近岸海水骤升造成的漫滩、漫堤和溃堤淹没，还包括海啸波到达近岸和港口引发的强流对基础设施和船只的冲击和破坏[5-6]。

自主开展海上丝绸之路地震海啸监测和预警分析工作迫在眉睫。实际上，在太平洋区域海啸预警与减灾系统框架下，南中国海区域已经拥有独立的海啸预警系统[7]（责任范围见图1），由自然资源部海啸预警中心负责运维。以联合国教科文组织海洋学委员会南中国海区域海啸预警中心（South China Sea Tsunami Advisory Center/United Nations Educational, Scientific and Cultural Organization-Intergovernmental Oceanographic Commission，SCSTAC/UNESCO-IOC）的名义向南中国海周边9 个国家提供海啸预警服务。

本文将基于图形处理单元（Graphic Processing Unit，GPU）并行加速技术建立印度洋海啸数值预报系统。首先，收集统计了印度洋和南中国海区域内的历史地震海啸事件，然后利用线性浅水方程建立了覆盖印度洋的海啸传播计算模型；进一步沿环印度洋域内国家的海岸线选取了540个预报点对岸段危险进行警示，对重点城市和港口给出海啸首波预计抵达时间和最大波幅；最后，利用2004 年苏门答腊地震海啸及之后的3次事件对数值预报结果进行释用和性能分析。

2 预报系统建立

海啸数值预报系统包括海啸源计算、海啸传播计算和海啸预警分析3个模块。海啸源计算是为了获取初始海表面位错分布，作为海啸初始场驱动海啸传播方程；继而借助GPU 加速技术进行海啸传播计算，产出海啸传播时间和最大波幅场；最后，预警分析模块通过对波幅的后处理获得岸段危险性分析结果。

2.1 地震监测和海啸源计算

实际业务中，海啸数值预报系统的启用通常需要两个条件：一是发生在海底的浅源地震且震级达到Mw7.1 级以上；二是依赖震源特征参数用于快速计算海啸源。

条件一要求对地震事件具备实时监测能力，能够在地震发生后迅速给出地震发生的时间、位置、震级和深度。自然资源部海啸预警中心开展了全球地震监测系统建设，现已具备全球地震快速监测能力[8-9]，本文采用其速报参数。

条件二要求能够快速估计震源的破裂长度、宽度和滑移量，以及反演地震的震源机制。本文选择了Blaser等[10]推导的大洋俯冲带逆冲型定标律来估算震源的破裂尺度；然后利用地震矩公式计算均一滑移量[11]；再采用W-phase 方法准实时反演震源机制解[12-15]。

满足上述两个条件之后，即可利用OKADA 模型计算海底位错，即初始海表面位移作为海啸源[16]。

2.2 数值预报模型

海啸波在大洋中传播时，波幅远小于水深，波长远大于水深。因此，可以忽略非线性效应，线性长波方程便可很好地模拟海啸波，但是应考虑科氏力的影响。球坐标系下的方程表达式为：

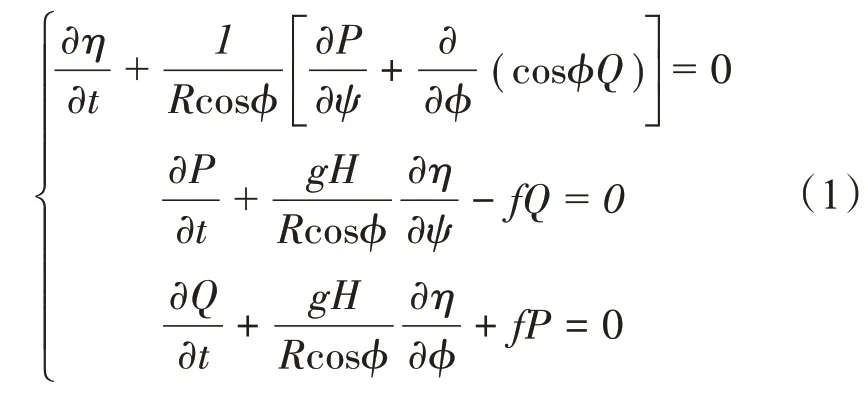
式中：η为相对于平均海平面的自由表面位移；φ为纬度；ψ为经度；R为地球半径；P为沿纬度单位宽度的通量；Q为沿经度单位宽度的通量；f为科氏力系数；g为重力加速度。该模型对海啸波在大洋的传播模拟已经经过验证[11]。

模型计算区域覆盖整个印度洋和南中国海以及苏禄海和苏拉威西海，具体范围40°S ～28 °N、15°～130°E，地形水深采用GEBCO_14 Grid。线性方程的差分方案采用球坐标系下蛙跳格式有限中心差分，辐射边界条件，具体配置详见表1。硬件计算环境为2 个14 核Intel(R) Xeon(R) CPU E5-2680 v4 芯片，主 频为2.4 GHz，128 G 内存；GPU 采 用Nvidia Tesla K40c 显卡，计算耗时见表1。对于震级较小的计算过程应采用2 arc-min 空间分辨率，时间成本变成约4 min。

表1 印度洋海啸预报模型配置和计算效率

2.3 预报点选取和后处理

当海啸波传播到水深较浅的近岸区域，非线性效应变得显著，线性方程不再适用。如果采用非线性模型直接计算沿岸波幅，则需要高精度地形资料配合以及更短的时间步长，时间成本将大幅提高。为了兼顾岸段预报的准确性和时效性，本预报系统采用格林公式[17]，将低分辨率模型输出的离岸点（Offshore）海啸波幅换算到水深极浅的沿岸预报点（Coast）。

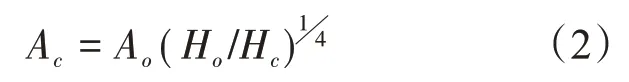
式中：Ac和Ao分别为近岸和离岸预报点最大海啸波幅；Ho和Hc分别对应离岸和近岸点水深。根据模型分辨率的不同，Wang 等[17]对离岸点的水深做了条件限制。对于4 arc-min 的模型分辨率，Ho应大于992 m；Hc使用固定值1 m。并且，离岸点和预报点之间的距离在不超过100 km 的条件应该尽量取小。

按照约60 km 的间隔距离沿着北印度区域内的澳大利亚、印度尼西亚和泰国等27个国家或者主权归属地选取了540 对岸段预报点（见图3）。离岸点和近岸点平均间隔约50 km，超过95%的离岸点水深在（100 m，1 000 m）的区间，平均水深450 m，根据经验，将近岸点水深调整为5 m（变形格林公式）。这540 个预报点中包括了环印度洋国家的78 个重点城市和港口。

3 预报结果和系统性能

选取2004—2010年发生在印度洋的4次Mw7.8级以上地震海啸事件对数值预报结果和性能进行说明，震源参数见表2。引发2004 年苏门答腊海啸的地震震级超过了Mw9.0，且地震破裂过程非常复杂[2-3]。因此，在计算海啸源时，采用了Grilli 等[18]的多点源策略。

表2 海啸事件震源参数

3.1 预报结果释用

以2004年苏门答腊大海啸为例，解释说明预报系统产出的定量海啸预报结果，包括大洋最大波幅图和岸段危险警示图（见图2、3），以及重点城市、港口和验潮站的海啸预计抵达时间。图片右侧标注了地震发生的时间、位置、震级以及震源深度和快速反演的震源机制解。从图2中可以看到海啸能量的几个主要传播方向，包括震中附近的苏门答腊岛、泰国西海岸、缅甸南部、孟加拉湾、斯里兰卡、印度东南海岸、马尔代夫、索马里、马达加斯加东南岛弧以及印度洋中脊西南支。

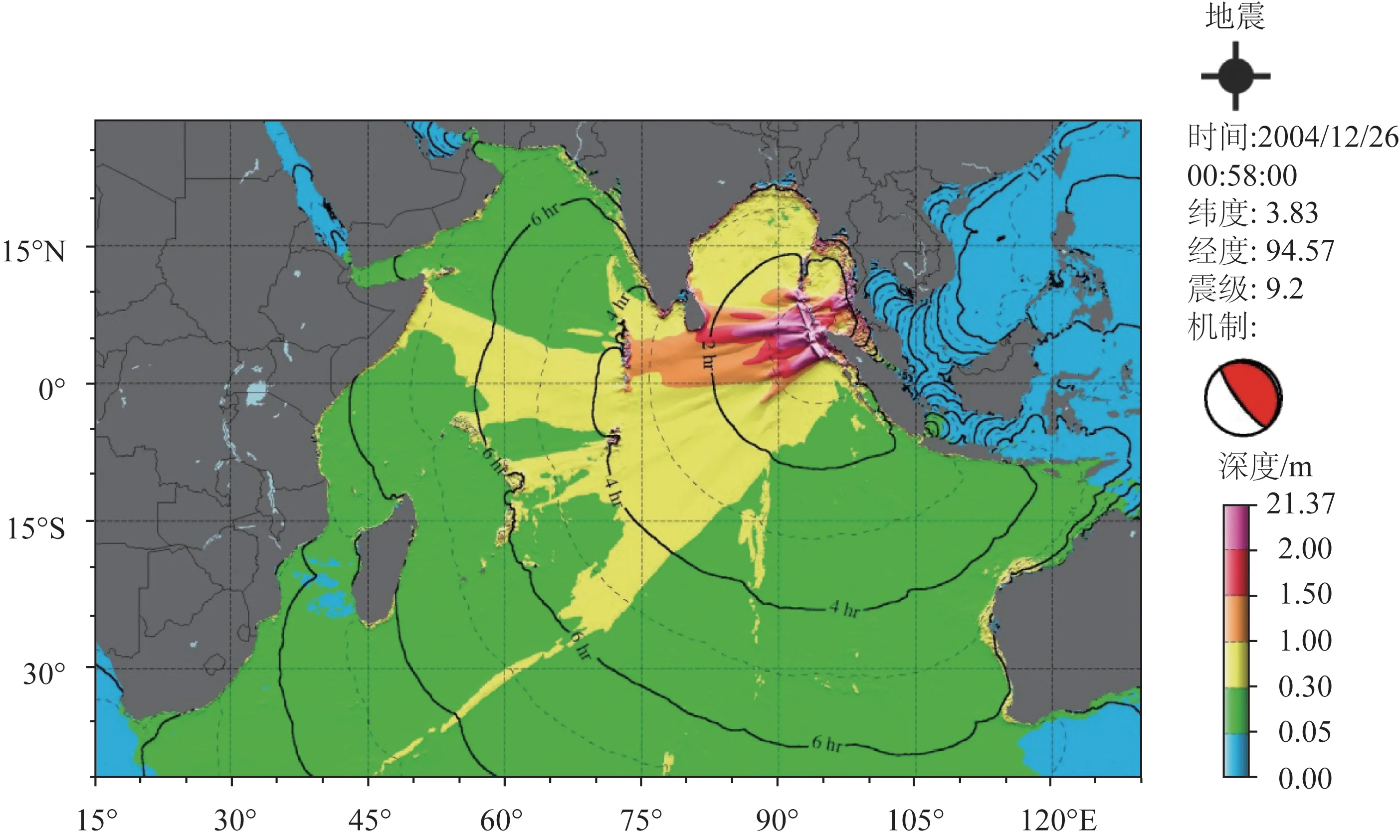
图2 印度洋区域海啸预计传播时间和最大波幅预报（以2004年苏门答腊海啸为例）

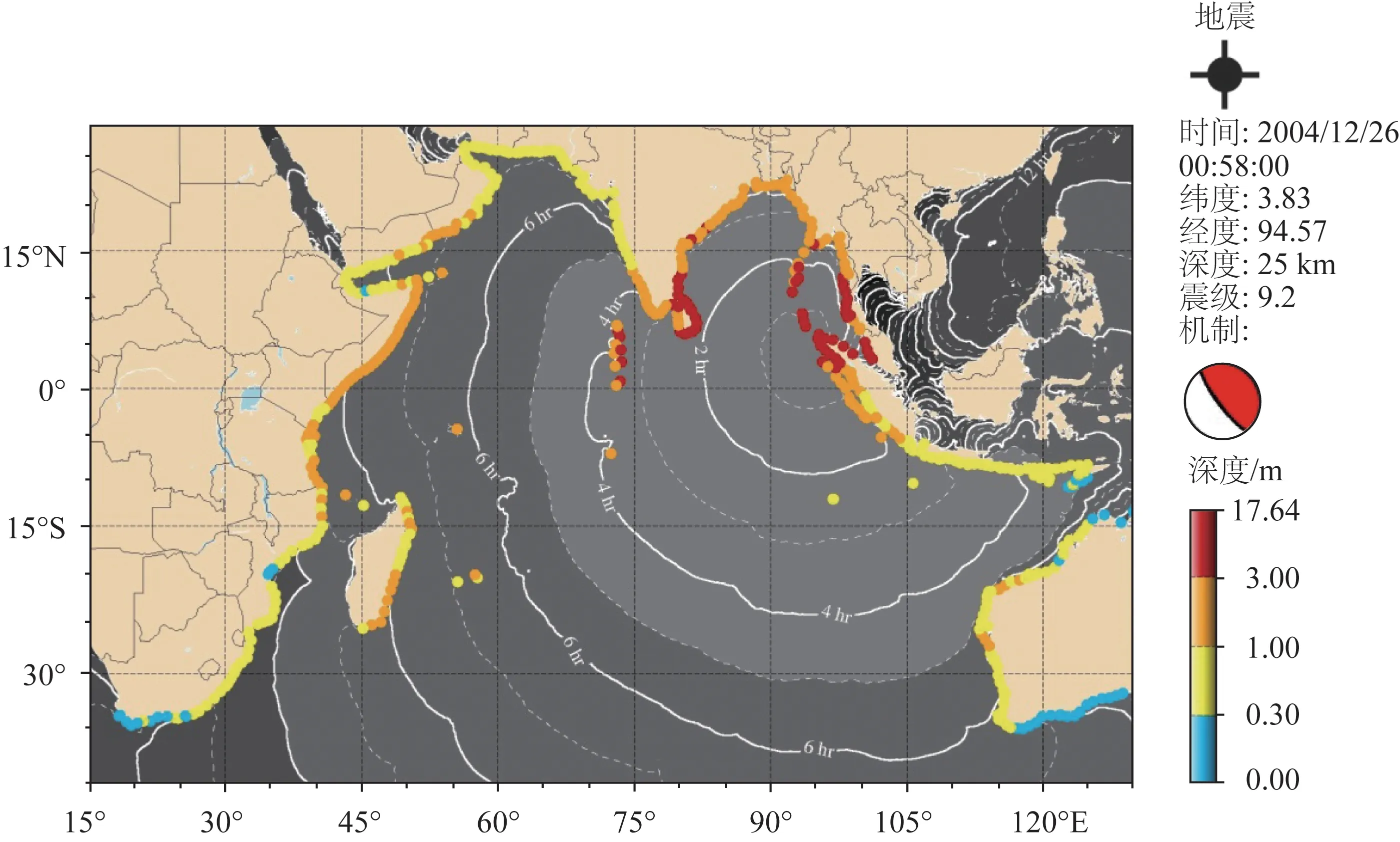
图3 印度洋区域海啸预计传播时间和岸段波幅预报（以2004年苏门答腊海啸为例）

从图3 我们能够看到，震源附近的苏门答腊第一时间受到海啸冲击，尤其位于其西北的亚齐省以及临近的韦岛产生了超过3 m 的海啸波幅，最大波幅超过10 m。这意味着在没有巨型防波堤的情况下，上述区域将产生大面积海啸入侵和淹没。除此之外，泰国西海岸、马来西亚半岛西北海岸、缅甸南部西岸、安达曼尼科巴岛、斯里兰卡东岸、印度东南海岸以及马尔代夫群岛东侧都也都出现了超过3 m的海啸波，大面积淹没不可避免，预报结果与灾后调查结果基本一致[19]。

3.2 性能说明

W-phase 方法只能快速反演得到基于点源的震源机制，如果一个地震的破裂属性存在显著的空间变化，那么单点源震源机制刻画的海啸源代表性则较差。震源附近的海啸传播时间和波幅计算结果往往会产生较大偏差。除此之外，如果验潮站位于有遮挡的海湾、受防波堤保护的港口、或者验潮站离岸地形水深条件复杂，以及格林公式换算路径上存在很宽的陆架或陡峭的陆坡，也都会对海啸预报结果造成偏差[17]。一方面原因是模型分辨率不足，另一方面是不满足格林公式的适用条件[11]。

基于以上原因，并非所有的验潮站均可用于验证本文的预报系统，或者说，验潮站的观测结果不完全能够指示岸段的危险性。以苏门答腊地震海啸为例，泰国的RANONG、KURABURI、PHUKET、KRABI 和TRANG 5 个验潮站记录的海啸波高普遍约为0.7 m，最大为1.1 m；而灾害调查结果显示，上述验潮站所在岸段波高均值超过5 m；斯里兰卡的COLOMBO 观测到1.5 m 的海啸波，灾后调查显示其所在岸段海啸波高普遍超过4 m。上述原因可能是验潮站在记录到最大海啸波高前就已经失去功能。

因此，在选择验潮站比对预报结果时，我们将不满足格林公式适用条件的验潮进行了剔除。4 次海啸事件共筛选了44个验潮站次的数据作为观测，其中2007 年的南苏门答腊Mw8.4 地震海啸事件缺少海啸传播时间数据，导致只有32 个站次数据可用。下面选择海啸传播时间和海啸最大波幅两个指标进行分析。

计算的海啸传播时间与观测相比，平均绝对误差约为15 min，最大绝对误差约为40 min（见图4，具体的计算和观测结果对比见表3）。对于国家尺度的海啸预警，我们认为这样的误差量级基本可以接受。更准确的海啸传播时间依赖精细的海啸源刻画和高精度地形水深资料。

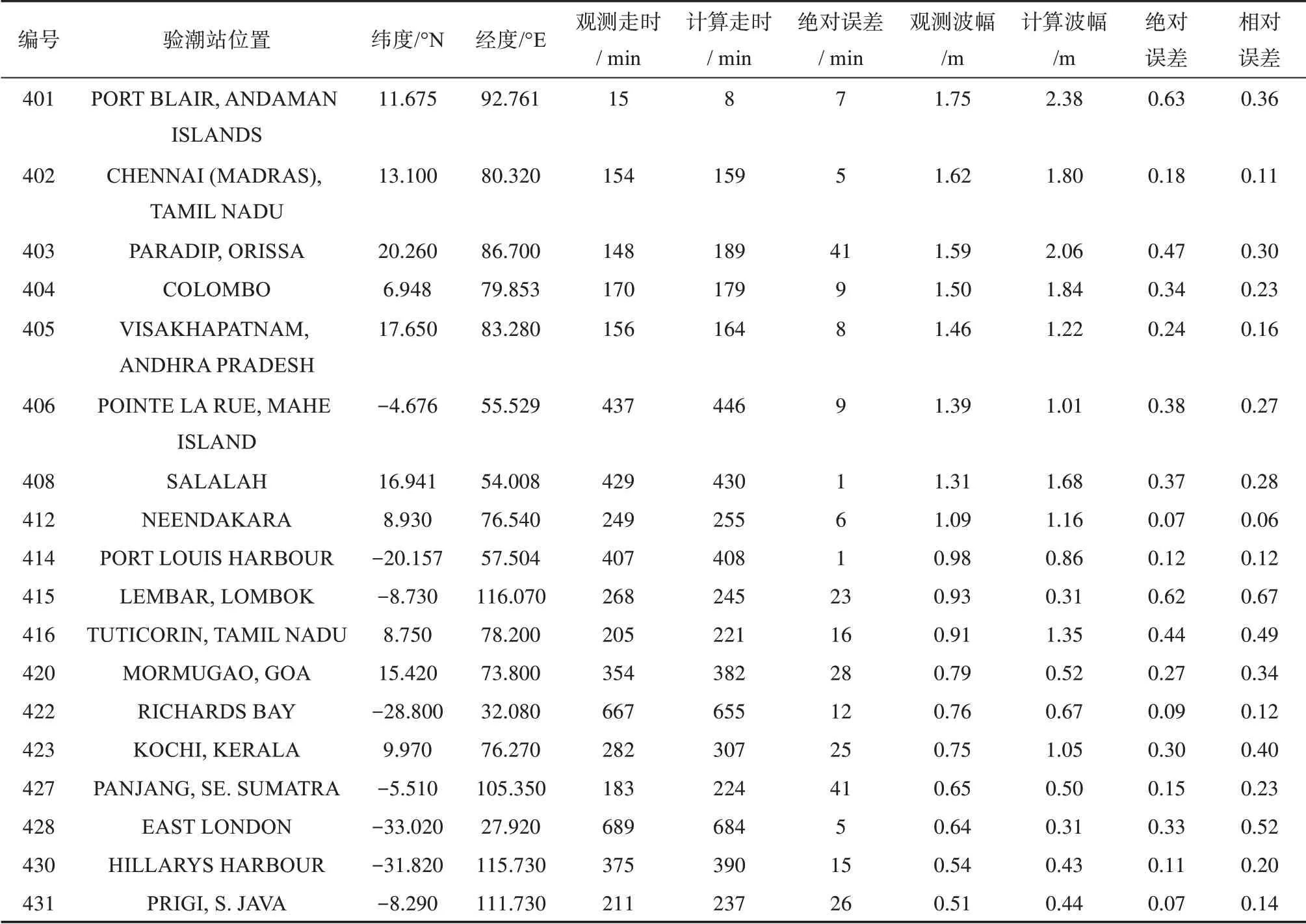
表3 海啸传播至验潮站的走时计算结果与观测对比

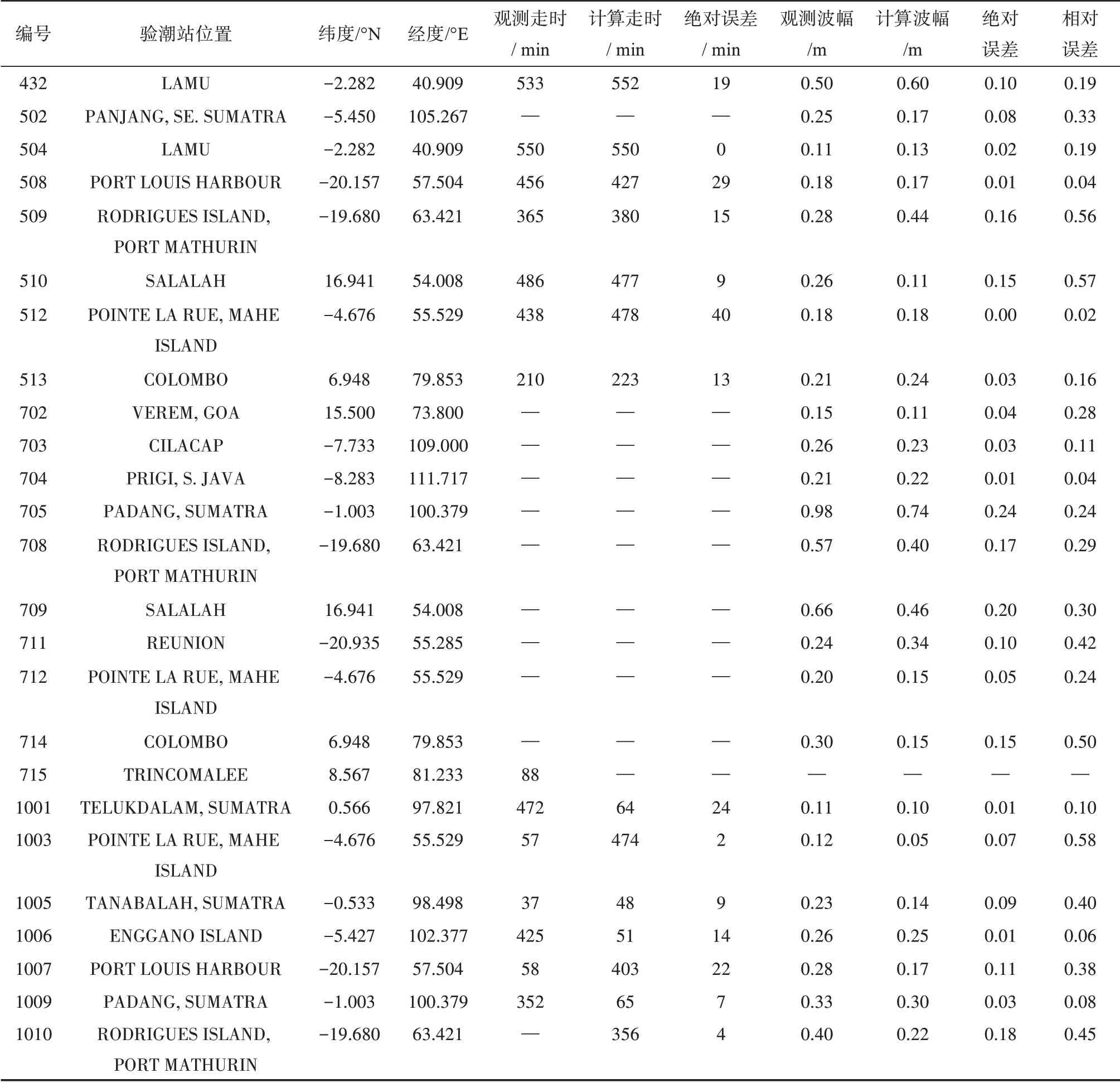
续表3

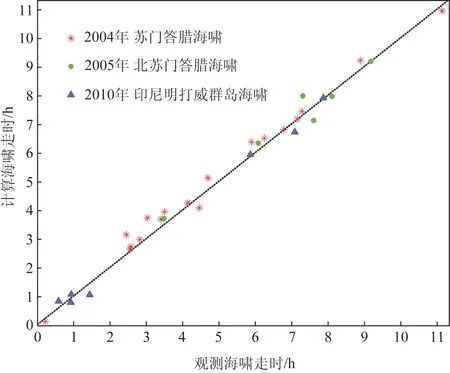
图4 海啸传播至验潮站的走时计算结果与观测对比

按照国际惯用海啸危险等级和王宗辰等[11]对波幅预警的评价标准对计算结果进行了分析（见图5）。44 个站次的海啸波幅绝对计算误差约为17 cm，相对误差为27%；其中危险性合理判断比例达到86%，高估和低估比例分别为9%和5%，对于大尺度的国家预警而言，这样的波幅预报水平完全可以接受。如果再考虑图3 和灾害调查结果的比较，系统性能分还可提高。

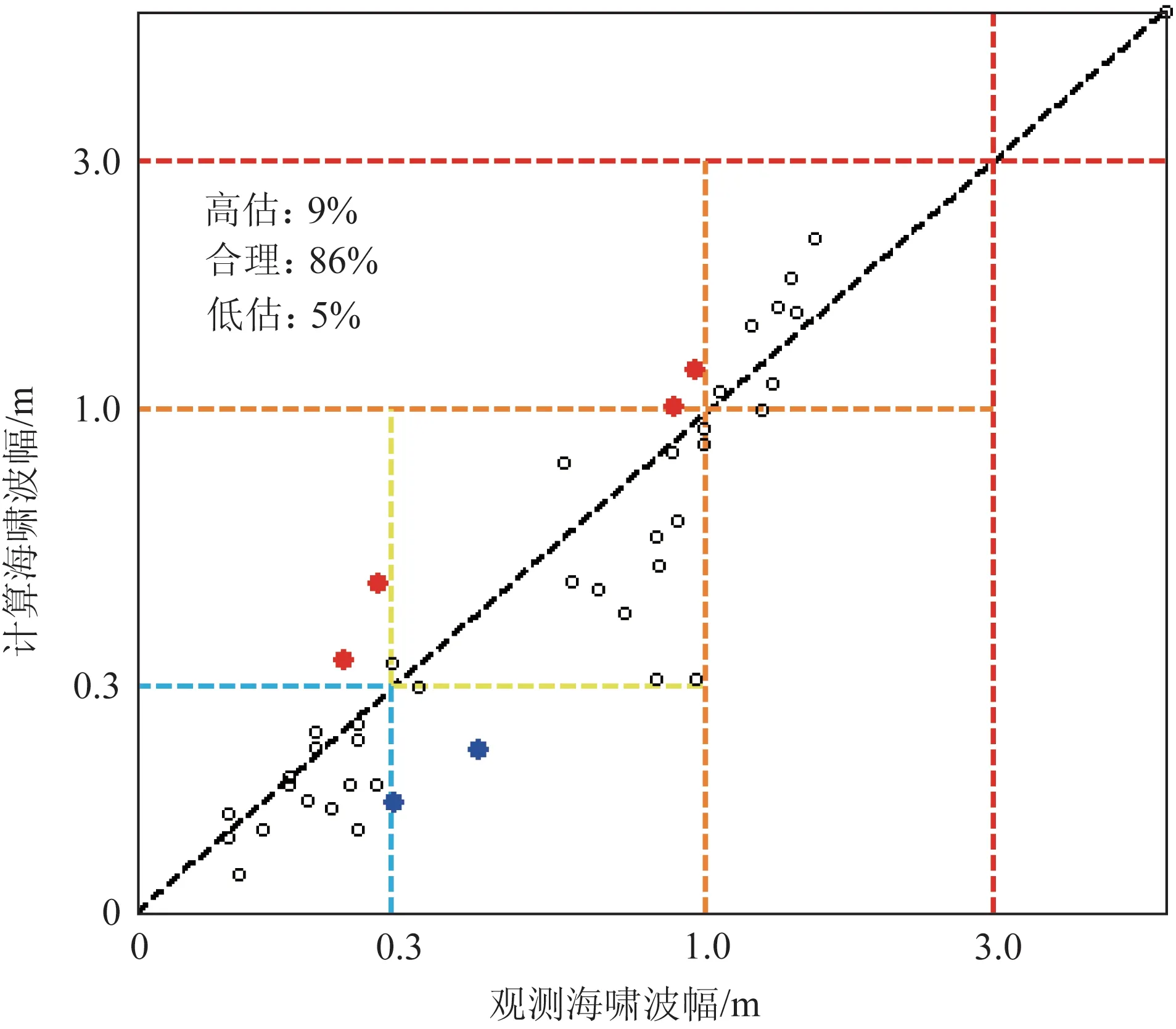
图5 验潮站海啸最大波幅计算结果与观测对比

海啸传播计算用时约40 s，GMT 绘制图件用时约6 s，整个数值预报流程耗时可以控制在50 s 之内。如果在震后0.5 h可获得震源机制解，数值预报的流程耗时基本可以忽略。依赖网站、邮件和短信等通讯手段，海啸数值预报结果和危险性信息可以在1 min 之内发出。以苏门答腊地震海啸为例，除了位于震源周围100 km 之内的苏门答腊岛和安达曼尼科巴岛之外，其他国家和相关机构仍有1.5～2.5 h的时间做出减灾部署。

4 结论

本文依托自然资源部海啸预警中心的全球地震监测和反演系统实时获取地震速报和震源机制解，结合地震震级-破裂尺度定标律和OKADA 公式计算海啸源；再利用基于GPU 加速的线性海啸传播计算模型建立了印度洋区域的海啸数值预报系统；沿着印度洋周边国家的海岸线，按照50～60 km 的标准选择了540 对离岸-近岸预报点，利用变形格林公式对岸段海啸波幅进行定量预报。

选取2004 年以来发生在苏门答腊岛周边4 次Mw8.0级以上地震海啸事件对预报系统的定量预警产品进行释用，并对系统性能进行了测试。结果显示，本系统能够在得到震源机制解之后1 min 内产出整个印度洋区域海啸预警分析结果。4 次海啸事件的后报结果显示，海啸传播时间的绝对计算误差约为15 min，危险性合理判断比例达到86%。

印度洋地震海啸数值预报系统的建立不仅能够为国内“海丝路”相关单位和机构提供准实时的定量海啸预警报服务，借助网站和社交媒体，该系统还可以为印度洋周边国家提供海啸危险性参考。