基于非迭代海-气通量算法蒸发波导预测模型在不同海域的适应性研究

刘立行，周树道，盛峥，张树时，邓以勤，郝玉珠

（1.中国人民解放军63983部队，江苏无锡214000；2.国防科技大学气象海洋学院，江苏南京210000；3.中国气象科学研究院南京气象科技创新研究院，江苏南京210000；4.中国气象科学研究院灾害天气国家重点实验室，北京100081；5.平潭综合实验区气象局，福建平潭350400；6.内蒙古自治区气象服务中心，内蒙古呼和浩特010051）

1 引言

蒸发波导是发生在海洋上的一种常见的大气折射现象，是由于水汽蒸发引起大气湿度随高度锐减形成的一种大气层结[1]。它产生于特定的气象海洋条件中，在海-气相互作用引起的海面水汽蒸发下，海面上大气湿度随高度锐减形成较大的湿度垂直梯度变化。它属于一种特殊的无基础层的表面波导类型。根据大气变量找到一个垂直折射率梯度的表达式，通过对该式求解得到折射率梯度临界值对应的波导高度。一般用温度T、气压P、水汽压e的数学物理方程表征大气折射指数N：

式中：P为气压（hPa）；e为水汽压（hPa）；T为气温（K）；A、B为常数，一般取A=77.6 K/hPa，B=4 810 K/hPa。

在大气环境中，大气温度、气压和水汽压会随着高度h不同而变化。为了避免这一影响，用修正折射率剖面M来表征大气波导的廓线特征。大气修正指数的垂直梯度定义为：

式中：h表示地面以上的高度；a=6.371×106m，表示地球半径。一般蒸发波导高度是当大气层结dM/dz= 0时的高度。

蒸发波导的发生高度较低。目前采用最多的是通过测量海上气象参数和海表温度，并基于海-气相互作用相似理论发展的模型进行预测[1]。由于海上蒸发波导对无线电探测和短波通信有重要影响[2]，欧美国家自20 世纪50 年代起开始进行蒸发波导的科学研究[3]。20 世纪70 年代，Jeske[4]利用海上气象要素计算了蒸发波导的厚度。Liu 等[5]在1979年提出了LKB模型，1984年在加利福尼亚海洋战场评估中心建立了NWA模型[6]；与此同时，Paulus[7-9]建立了P-J 模型、1992 年Cook 等[10]建立了NRL 模型、Musson-Genon 等[11]建立了MGB 蒸发波导模型、1996 年Babin 等[12]建立了Babin 模型（A 模型）、2000年Frederickson等[13]建立了NPS模型。此外，俄罗斯国立水文气象大学建立了RSHMU 模型、欧洲中尺度天气预报中心建立了ECMWF 模型和COARE 模型等[14]。在我国，刘成国等[15]建立了伪折射率模型；戴福山等[16]建立了Local 模型；Ding 等[17]建立了UED模型等。

蒸发波导预测模型主要是建立在Monin-Obukhov相似理论上并通过整体空气动力学方法来进行预测。模型通过迭代算法能够较好地遵循MO相似理论，减少频繁近似引起的计算差，使得模型输出结果更加有效，例如根据TOGA COARE 算法等通过迭代微分给出合理的特征参量值。但此类模型迭代计算需要冗长的运算次数和大量耗损CPU 时间，在大范围和多时次的蒸发波导预测诊断计算上效率降低。Liu-Li 蒸发波导预测模型基于非迭代海-气通量算法建立，模型的建立思想与传统蒸发波导模型有所不同。该模型通过在折射率方程中结合K 理论通量观测法，输入一定高度的风速、温度、相对湿度、压强和海表温度等要素值来算取蒸发波导的高度。因此，本文将通过海区实验获得的蒸发波导高度数据与通过Liu-Li模型计算得到的高度数据进行对比，并再结合美国气象环境预报中心（National Centers for Environmental Prediction，NCEP）的FNL 再分析资料，验证Liu-Li 模型在不同海域的适应性及适用条件。

2 基于非迭代海-气通量算法的Liu-Li模型

Liu-Li 模型是基于非迭代海-气通量算法建立的蒸发波导模型，模型中采用的非迭代海-气通量参数化方法由Li 等在2014 和2015 年提出[18-19]。方案是依据PCB 迭代方案（Paulson70 参数化方案、CB05通量方案）的计算结果进行回归分析后形成的。与以往蒸发波导预测模型不同的是，Liu-Li 模型并没有通过设定初值和迭代计算来确定M-O长度L和特征尺度u∗、θ∗和q∗，而是根据参数化方案中整体理查森数Rib的值来判断ξ的不同表达式，以确定M-O 长度L和特征尺度u∗、θ∗和q∗。这在一定程度上提高了计算效率，可以为长时间和大范围的大气波导模拟预测节省运算时间[20]。

该通量算法方案中通量整体输送系数定义为：

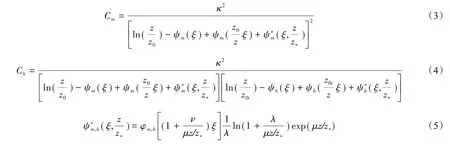
式中：R是普朗特常数；κ是冯·卡曼常数；z是参数输入高度；z0是动力学粗糙度，z0t是热力学粗糙度，z0q是水汽粗糙度；这里取λ= 1.5，μ=μm= 2.59，μ=μh= 0.95，ν = 0.5；稳定度修正函数采用CB05通量方案[19]的定义方法。

已知，大气折射率方程可以改写成：

式中：T是空气温度；p是大气压强；ρ是空气密度；e是水汽压；q是比湿；Ra是干空气气体常数；ε是气体常数比。

在模型中，将湍流通量、感热通量和水汽通量用以下方程式来表达：

式中：ρ为空气密度；cp为定压比热容；u∗为风速特征尺度；θ∗为温度特征尺度；Le是蒸发潜热。

把一阶闭合K 理论和近地层湍流通量表达式（11）、（12）代入式（6），可以得到：

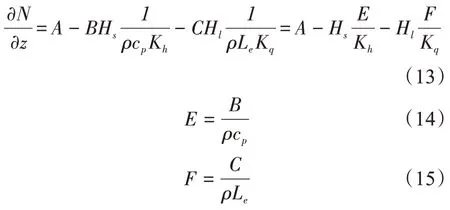
蒸发波导高度处通常满足：

由式（13）—（15）联列M-O 相似理论并代入式（16），在蒸发波导高度处则有：

代入稳定度修正函数可以得到中性条件下(z/L= 0)，蒸发波导高度为：

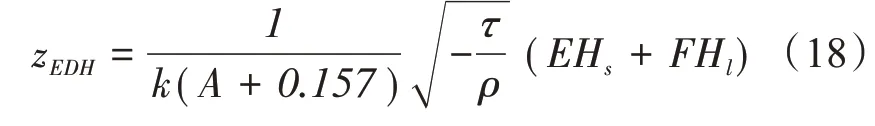
稳定条件下(z/L＞0)，蒸发波导高度为：

zEDH=

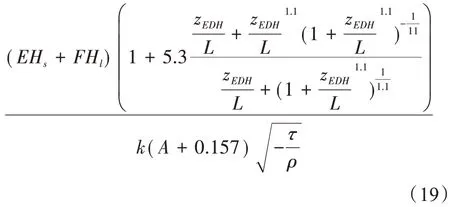
不稳定条件下(z/L＜0)，蒸发波导高度为：

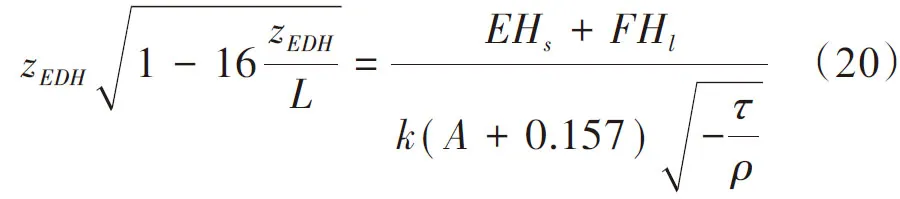
通过选择合适的迭代方法，式（19）、（20）可求得不同大气层结状态下的蒸发波导高度。

3 Liu-Li模型的适应性研究

3.1 模型的敏感性分析

为了分析非迭代海-气通量算法Liu-Li 模型的适用性，本文模拟了诊断模型对不同气象海洋要素的敏感性响应。图1 代表了Liu-Li 模型随风速、湿度和气海温差的变化情况计算的蒸发波导高度，模型要素的观测值高度统一输入为6 m。结合实际情况，对模型结果进行质量控制，将模型计算高度大于40的取为40 m，小于0的值取为0 m[21]。

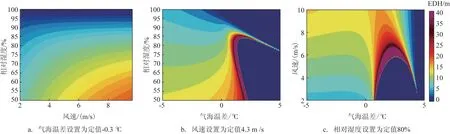
图1 Liu-Li模型计算得出的蒸发波导高度随风速、气海温差和湿度的变化情况

图1 可以看出，风速、气海温差和相对湿度3 种要素的变化对Liu-Li模型的诊断结果都有着较大影响。海上大气温度和海表温度两者之间差异的变化直接影响了海面大气环境的层结情况，Liu-Li 模型对相对湿度和风速也存在着明显的敏感性响应。主要表现为：当海上大气处于不稳定层结条件下时，Liu-Li 模型得到的蒸发波导高度随着相对湿度的增大而降低、随着风速的增大而增高；而当海上大气处于稳定层结条件下时，Liu-Li 模型计算的蒸发波导高度显示出对气海温差有强烈的敏感性响应，蒸发波导高度随着气海温差的增大会迅速增高至过高值40 m。随着海上大气层结条件的进一步稳定，达到强稳定层结条件时，Liu-Li模型计算的蒸发波导高度得到大范围的零值，但在一些特殊的海-气条件下蒸发波导高度也会高于40 m。总体上，Liu-Li模型在不稳定大气层结条件下对相对湿度和风速敏感性的结果与其他模型的敏感性研究结论一致；在稳定大气层结条件下，Liu-Li模型对气海温差的敏感性响应更加明显[20]。Liu-Li 模型计算得出的蒸发波导高度随风速、气海温差和湿度的变化情况以及与其他模型结果的对比在文献[20]中已作了详细讨论，此处不再赘述。

3.2 Liu-Li模型在我国渤海海域的适应性研究

本文选取了中国电波传播研究所在渤海某海域采集的海上观测塔数据及浮标站数据进行实验。数据为2011年7月6—14日，每隔1 min采集一次数据，包括了温度、湿度、气压、风和海表温度等气象要素，并根据采集时刻实际海平面状况给出距离海面高度，以便为统一输入高度提供订正，同时记录了中国电波传播研究所根据观测塔测量得到的蒸发波导高度。观测塔共分6 层，分别在6 m、10 m、15 m、20 m、27 m 和34 m 设置了气象传感器，最低层温度为海表面温度。通过铁塔数据观测数据拟合得到温、湿度廓线，并计算出大气修正折射率得到对应波导高度。经过数据处理，剔除了部分异常观测数据，共取样数据5 108个，并将这些观测数据分别代入Liu-Li模型、Babin模型、NPS模型、P-J模型和伪折射率模型等5种蒸发波导模型开展了模拟仿真。

从图2可以看出：2011年7月6—14日内试验海域的相对湿度均维持在75%以上，并且大多数保持了较高的相对湿度值；海面气压在试验中期发生了明显的变化：前期气压值维持在997 hPa 左右浮动，后期气压值维持在1 007 hPa左右浮动，可以看出该海域在试验中期受到了一个较强天气系统的影响；海面风速整体波动比较明显，前期最小风速低于1 m/s，最大风速高于12 m/s，中后期较为平稳；在试验时间范围内，该海域的气海温差大多小于0 ℃，最大气海温差接近5 ℃，可以看出海上大气环境为不稳定层结条件；7月6—14日该海域蒸发波导高度平均值在9 m 左右，最小为3.5 m，最大为17.1 m；而Liu-Li模型计算所得的蒸发波导高度平均值在6.6 m左右，最小为1.1 m，最大为32.3 m。

对比实测波导高度和Liu-Li模型计算所得波导高度的变化序列来看（见图2），两者变化趋势基本一致，整体较为平稳。两者在第700 个观测时次均开始出现断崖式减小，蒸发波导高度减小明显，且在一定时期内保持了平稳的变化趋势；在第1 250个观测时次前后，该海域蒸发波导高度也出现了短时间的高低波动，个别时次的蒸发波导高度明显异于平均水平，相应的Liu-Li 模型计算所得波导高度也在该时间段内发生了剧烈的变化，特别是出现了零值和40 m以上的过高值。

图2 2011年7月6—14日渤海试验中湿度、气压、风速、气海温差、实测波导高度和Liu-Li模型计算所得波导高度的变化序列

对比实测波导高度、模型计算所得波导高度的变化序列与湿度、气压、风速和气海温差的变化序列，可以看到蒸发波导对不同气象要素敏感性响应的变化。当大气处于不稳定层结条件下时，模型给出的波导高度显示出与相对湿度变化趋势一致，与风速变化趋势相反的特点，对气压的敏感性响应则不明显；在稳定层结状态下，蒸发波导高度除了对相对湿度和风速的变化响应较大外，对气海温差变化的响应更为明显，且容易出现零值和过高值。

为了更好地检验Liu-Li模型的适用性（见图3—5），将Liu-Li 模型的计算高度与其他蒸发波导预测模型的计算高度进行对比，并结合实际测得的波导高度，对不同模型的预测结果进行分析。从图3a可以看出：不同模型计算的波导高度变化趋势与实测波导高度的趋势基本一致，整体变化较为平稳；其他4 类模型两者也都在第700 个、第1250 个观测时次前后呈现出明显跃动和短时间的高低波动，Babin模型、NPS 模型和伪折射率模型也在该时段内出现零值和40 m 以上的过高值，而P-J 模型由于在稳定层结条件下加入了人为修正，避免了异常值的出现。与实测波导高度相比，可以看出实测波导高度整体平均高于所有模型计算所得的蒸发波导高度，P-J模型的计算结果与实测波导高度较为相近，除初始观测时间外，各时次的波导高度差都比较小；其次为伪折射率模型，计算结果与实测波导高度相差较小；Liu-Li 模型、Babin 模型和NPS 模型的计算结果则与实测波导高度有明显差异，其中Babin 模型最为明显。Liu-Li模型计算的波导高度与实测波导高度及其他模型计算的波导高度相差较小。Liu-Li模型计算的波导高度与Babin 模型和NPS 模型计算的波导高度基本相同，平均高度相差很小，伪折射率模型次之，相差最大为P-J 模型；特别是在稳定海气层结状态下，由于P-J 模型计算进行了人为订正，Liu-Li 模型与P-J 模型计算得到的波导高度相差则比较大，表征为异常值。

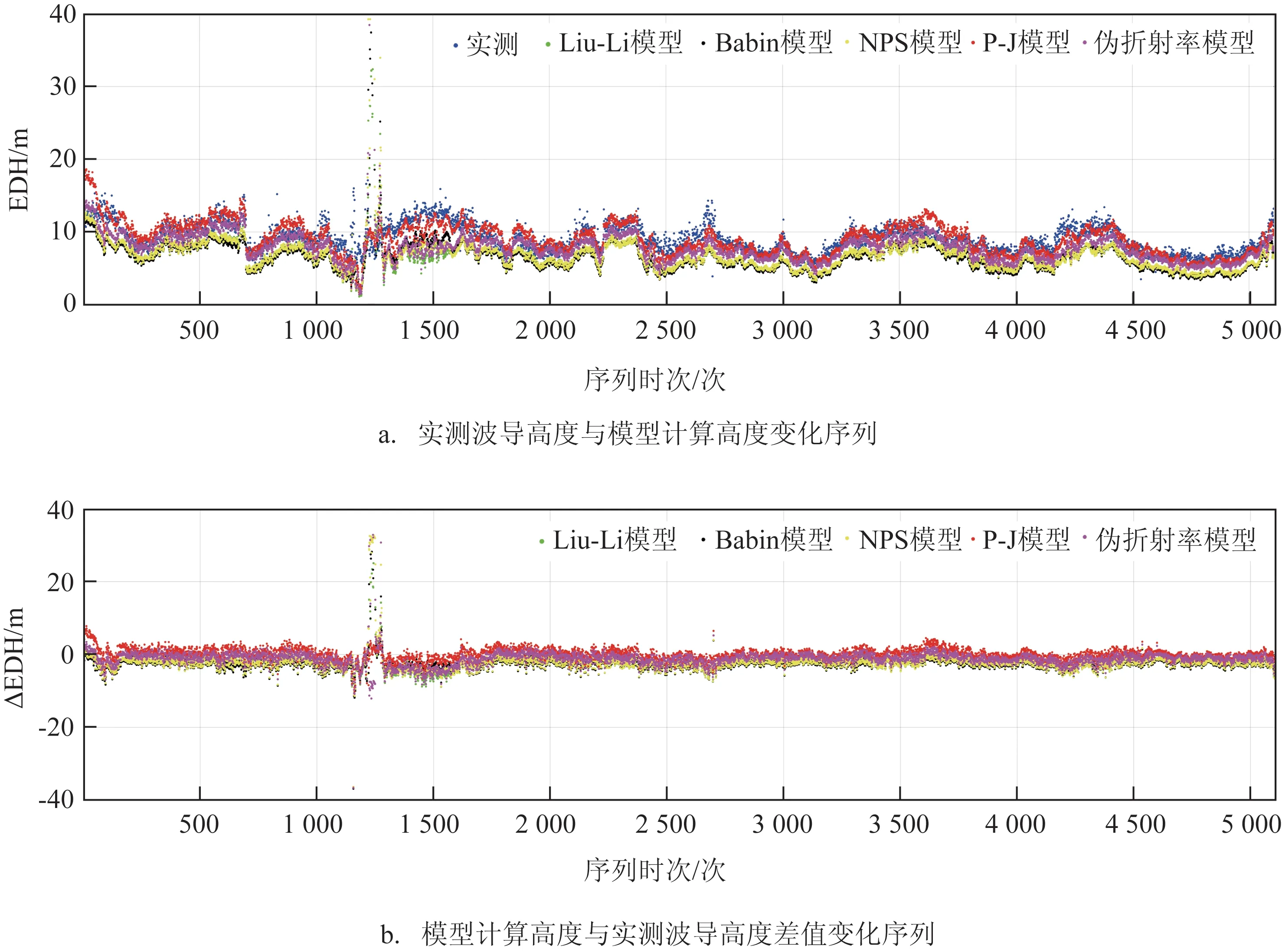
图3 2011年7月6—14日渤海试验中实测波导高度与模型计算高度的变化序列及高度差

图4 2011年7月6—14日渤海试验中不同模型计算所得高度与实际波导高度对比

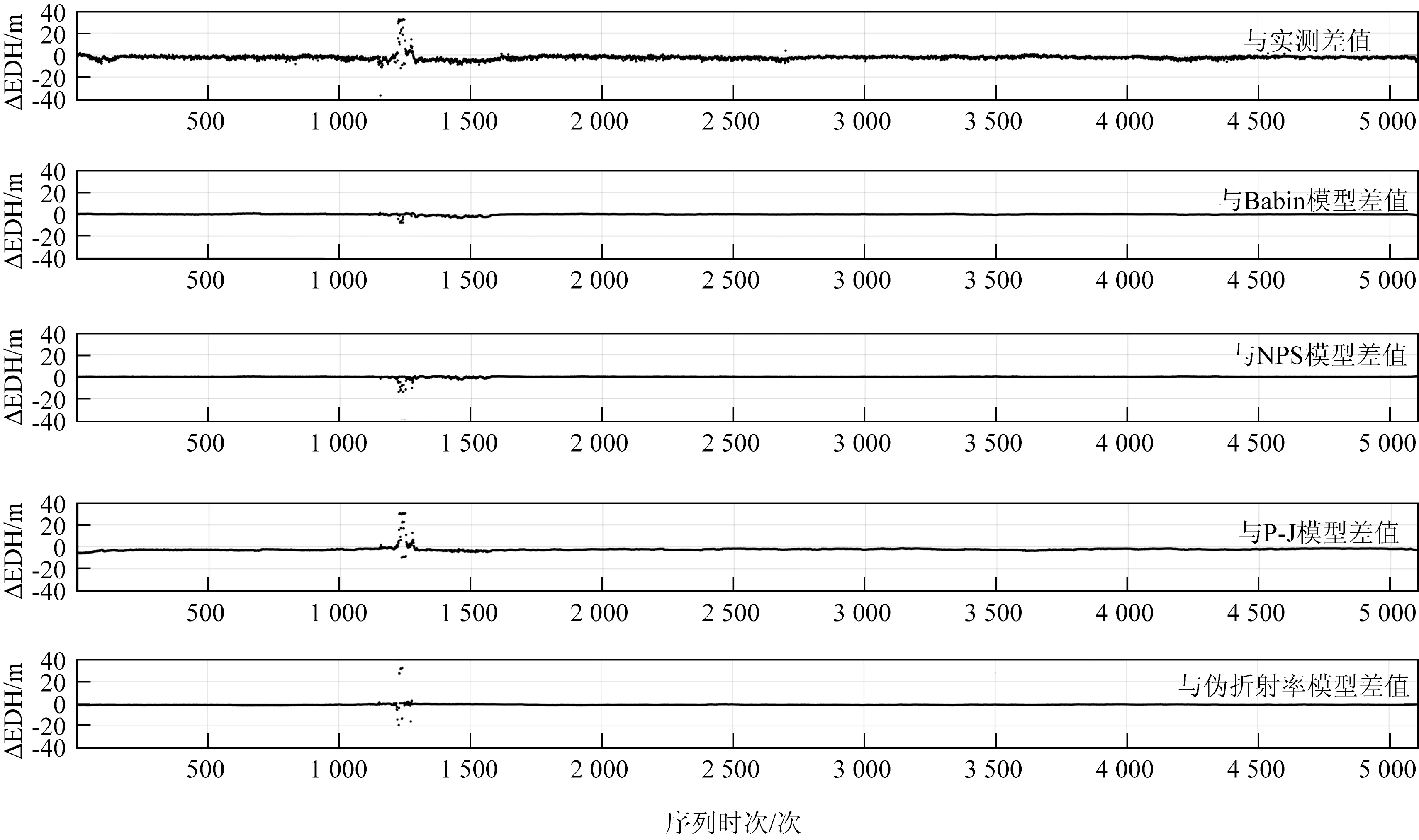
图5 2011年7月6—14日渤海试验中Liu-Li模型计算所得波导高度与实测波导高度以及其他模型计算所得波导高度差值的变化序列

根据图3b 和图4 可以看出，Liu-Li 模型的计算结果与实测波导高度平均差约为2.3 m；当海气层结处于不稳定状态时，Liu-Li 模型的计算结果偏小但差距不大；当海气层结处于稳定状态时，Liu-Li模型的计算结果偏大，特别是气海温差越大时，两者高度差越大，Liu-Li模型的计算易出现异常值。Babin模型的计算结果与实测波导高度平均差约为2.4 m；同样，当海气层结处于不稳定状态时，Babin 模型的计算结果偏小；当海气层结处于稳定状态时，Babin模型的计算结果偏大，特别是气海温差越大时，易出现异常值。NPS 模型的计算结果与实测波导高度平均差约为2.2 m；同样，当海气层结处于不稳定状态时，NPS 模型的计算结果偏小；当海气层结处于稳定状态时，NPS 模型的计算结果偏大，特别是气海温差越大时，易出现异常值。P-J模型的计算结果与实测波导高度平均差约为0.04 m；当海气层结处于不稳定状态时，P-J模型的计算结果也会出现部分偏小；当海气层结处于稳定状态时，P-J 模型计算结果的偏大值相比前3 种模型较小，这是由于引入人为订正后不易出现异常值。伪折射率模型的计算结果与实测波导高度平均差约为1.2 m；当海气层结处于不稳定状态时，伪折射率模型的计算结果也会出现部分偏小；在不同海气层结条件下计算结果的变化规律与其他模型较为一致，但其更容易在海气层结稳定状态时出现零值。结合图5，对比Liu-Li模型、Babin 模型、NPS 模型、P-J 模型和伪折射率模型计算蒸发波导高度的差值来看，Liu-Li 模型与其他模型的预测高度基本接近。在不稳定海气层结状态下，Liu-Li 模型与其他模型同样可以较好地给出试验时间范围内的蒸发波导发生情况，与Babin模型和NPS 模型的差值几乎为0，能够有效地诊断出波导发生的高度；在稳定海气层结状态下，特别是强稳定海气层结状态下，Liu-Li 模型的诊断结果与P-J 模型相差较大，未能像P-J 模型的诊断结果一样较好地表征实际蒸发波导情况，预测值超出了正常范围。这主要是由于Liu-Li模型同样建立在相似理论基础上，在海气层结稳定状态下会不可避免地出现异常值，同时也未能引入P-J 模型在此条件下的人工订正，这也是Liu-Li 模型下一步亟需解决的问题。

3.3 Liu-Li模型在大西洋海域的适应性研究

本文利用NCEP 发布的FNL 分析资料数据，通过Liu-Li模型尝试性地对大面积特定海域进行适应性研究。文中选取了FNL 分析资料中西北大西洋附近65°～75°W，40°～45°N 的格点数据，分辨率达1°×1°，数据日期从2001年7月28日12时（世界时，下同）—8 月8 日12 时，共45 个时次，包括了该时间段内2 m 高度处的空气温度、海表温度和相对湿度，以及10 m 高度处的风场数据。

利用上述数据对相应时间段内蒸发波导高度时空变化开展研究，将45个时次的分析资料按每6 h进行统计平均，得到11 d 内各气象要素的平均变化状态，并将计算出的不同蒸发波导高度按照6×11的格点进行空间分布。

图6 是45 个时次再分析资料的6 h 变化趋势。由于观测地点位于美国东部时区，与世界时存在4 h的时差，可以明确看到在18 时（当地时间14 时），空气和海表温度都达到了日最高，因而导致海表空气中水汽蒸发加快，相对湿度达到日最低。同时也可以观察到，该地区海表风速在午夜—早晨是递减趋势，而在早晨—夜间是递增趋势。

如图7 所示，整体来看，06 时Babin 模型对该海域计算的蒸发波导高度总体保持较低水平，波动较小；东侧海域出现大范围的零值，在个别地区也出现了过高值；西侧海域则相对稳定的保持在10～25 m 的波导高度。NPS 模型在计算东侧和中部海域时出现了大范围的过高值，西侧海域则与Babin模型计算结果接近，较好地给出了高度分布。伪折射率模型的计算结果在东侧海域主要是异常值，以零值居多，在西侧海域的波导高度则变化跨度较大。P-J 模型给出的波导高度平均略低于其他3 类模型，最大值低于16 m；东侧海域的波导高度变化较小，西侧海域则波动较大；整个变化趋势与风速的变化趋势一致，对风速的敏感性响应最强烈。Liu-Li 模型与Babin 模型的计算结果近似，波动较小；东侧海域出现了极值区域，西侧海域则相对稳定的保持在10～25 m 的波导高度，且西侧波导高度更趋于平稳，与经过修订的P-J模型高度差更小。

如图8 所示，12 时Babin 模型所求整个海域的波导高度有了一定的增加，海域东侧的零值区域逐渐减少，计算出的过高值也发生了北移；相对而言，西侧海域的蒸发波导高度有所下降。较之于Babin模型，NPS 模型对相对湿度的敏感性响应更为强烈；当相对湿度极高时，NPS 模型计算出的蒸发波导高度会作出强烈响应；东侧区域波导高度的变化波动更为显著，出现了分散的过高值区域。伪折射率模型计算的波导高度在东侧海域整体较低，在其纬度较低处出现了异常值区域；在西侧海域的波导高度则与前两类模型相似。P-J 模型给出的波导高度平均大于前3 类模型，其表征的特点与前一时刻相同，对风速的敏感性响应最强烈。Liu-Li 模型计算的波导高度较06时更加平稳，且对相对湿度的敏感性响应强烈；较之于Babin 模型和NPS 模型其计算结果更加合理，无极值出现，在该时段内诊断效果略稳定于其他模型。

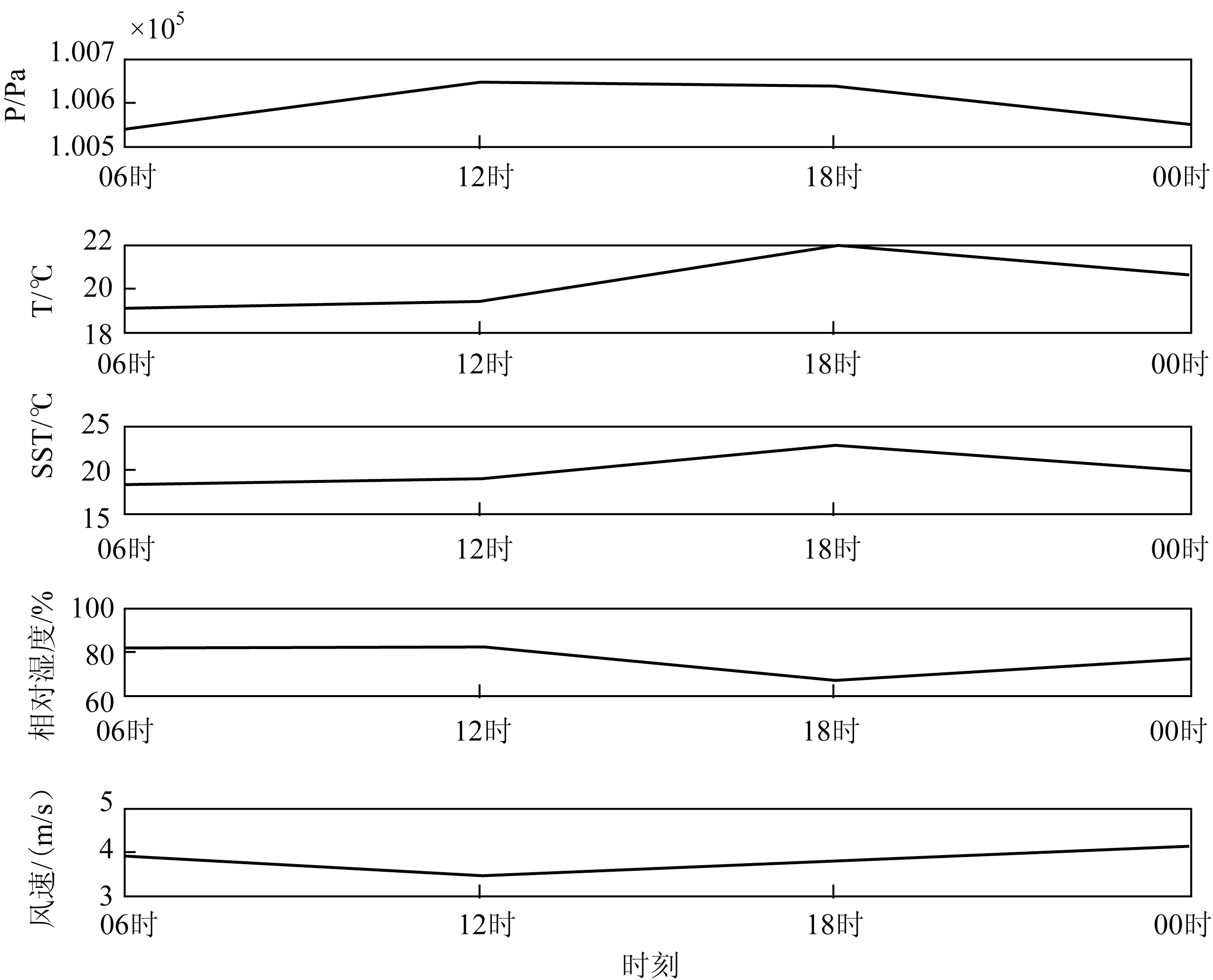
图6 2001年7月28日—8月8日西北大西洋气象要素间隔6 h的平均日变化序列

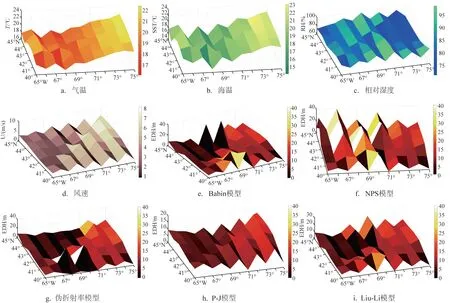
图8 2001年7月28日—8月8日12时西北大西洋气象要素和不同模型蒸发波导高度的空间分布

如图9 所示，在18 时Babin 模型计算的整个海域的蒸发波导值变化更为稳定，零值区域进一步减少，整体波导高度维持在10～20 m 的水平；但随着较高相对湿度的出现，西侧海域也逐渐出现过高值的异常表现。NPS 模型计算的蒸发波导高度整体比12时稳定，但平均高度低于Babin模型的结果；零值区域减少，但过高值区域增多。伪折射率模型计算的波导高度整体也相对平缓，平均高度高于NPS模型，与Babin 模型相近；在纬度较低的海域出现了过高值，零值发生的海域经度与Babin 模型相同。相比前3 种模型，P-J模型计算出的波导高度变化波动更有规律，整体高度也大于前3类模型；同时模型对相对湿度的敏感响应比风速更加明显；由于结果修正，零值和过高值的区域也较少。Liu-Li 模型计算的波导高度在此时间内变化情况稳定，整体波导高度值维持在10～25 m 的水平，平均高度与伪折射率模型相近；但随着较高相对湿度的出现，西侧海域也逐渐出现过高值的异常表现。

图9 2001年7月28日—8月8日18时西北大西洋气象要素和不同模型蒸发波导高度的空间分布

如图10 所示，在00 时Babin 模型计算的蒸发波导高度在整个海域的状况再次变得复杂，整体波动加剧，海域出现的零值和过高值也更加随机。NPS模型的计算结果也更为复杂，波导高度变化的跨度增大，过高值区域为多。相反的，伪折射率模型则以零值区域为多。P-J 模型的计算高度相较前3 类则相对平稳，变化趋势依旧与风速变化相一致。而Liu-Li模型计算的蒸发波导高度在整个海域也变得复杂，整体波动加剧；海域出现的零值和过高值接近于Babin 模型和伪折射率模型；波导高度整体平均值与伪折射率模型相近。总体来说，计算出的蒸发波导高度在该海域的西侧比东侧更加稳定，东侧海域易发生异常值的情况，而西侧海域的波导高度变化幅度相对较小。这与大西洋西岸紧贴北美洲大陆有一定的联系。

从所测时间段内的平均状况看，各气象参量在经向上都存在着明显的波动趋势，纬向上的变化并没有那么规律。气温和海温的变化趋势基本一致，这使得整个时间段内的海气层结状态变化较小。

就试验海域整体而言，5 种模型对气海温差、相对湿度和风速的变化都有明显的响应。P-J 模型计算的蒸发波导高度整体平均略低于Babin 模型、NPS模型、伪折射率模型和Liu-Li模型的计算结果，这主要是由于人为修正的影响。Liu-Li模型对该海区蒸发波导高度的诊断与Babin 模型、NPS 模型和伪折射率模型相近，尤其是Babin 模型。由于前人对Babin 模型在不同海域适应性的研究非常成熟[22]，这也有力支撑了Liu-Li 模型在大西洋海域的诊断应用。此外，也能够看出5种模型中P-J模型对风速的敏感性响应最为稳定，大多时次内其计算结果基本与风速变化趋势一致。其他4种模型则在海气条件复杂多变的情况下容易产生变化波动，24h内计算的波导高度在白天变化较小，在中午最为稳定；而在夜间起伏较大，容易出现异常值，这与夜间相对湿度更大、海表海陆风速大小的变化也有一定关系。

4 结论

本研究通过非迭代海气通量算法Liu-Li模型分析了该模型对海上不同气象海洋要素的敏感性响应，同时根据观测数据和分析资料，在不同海域对Liu-Li模型的蒸发波导高度预测诊断效果进行了分析，并与现有主流的Babin 模型、NPS 模型、P-J 模型和伪折射率模型的蒸发波导的预测诊断效果作了对比分析。研究发现：在我国渤海海域，Liu-Li模型的计算结果与实际观测波导高度以及其他4种模型计算结果的变化趋势基本一致，能较好地反应该时段内海上蒸发波导高度的变化趋势，并且在不同层结状态下对气象要素作出敏感性响应。在波导高度预报结果上，Liu-Li 模型在不稳定海气层结状态下计算得到的波导高度略低于实际观测波导高度，而在稳定海气层结状态下的计算波导高度结果偏大，特别是海气层结状态越稳定时，两者高度差越大，Liu-Li 模型的计算易出现零值和40m 以上的过高值。Liu-Li模型计算得到的波导高度变化趋势与其他4种蒸发波导预测模型相近，特别是与Babin模型和NPS 模型最为接近，且平均高度相差很小；在稳定海气层结状态下，由于P-J 模型计算进行了人为订正，Liu-Li模型与P-J模型计算得到的波导高度相差比较大，表征为异常值。而在西北大西洋海域，Liu-Li模型对气海温差、相对湿度和风速的变化都有明显的响应，模型对该海区蒸发波导高度的诊断与Babin 模型、NPS 模型和伪折射率模型相近，特别是Babin 模型；但相比于这3 种模型，Liu-Li 模型的计算稳定性更好，出现极值的概率更低。Liu-Li模型在大多时次内的计算结果与风速、相对湿度的变化趋势较为接近。Liu-Li模型计算的波导高度在海气条件复杂多变的情况下容易产生变化波动，24 h 内计算的波导高度在白天变化较小，中午最为稳定；而在夜间变化起伏较大，容易出现异常值的情况，这与夜间相对湿度更大、海表海陆风速大小的变化也有一定关系。

综上所述，虽然不同的蒸发波导模型利用了不同的参数化方案和普适函数建立模型，但由于其都建立在M-O 相似理论的基础上，因此模型预测结果的变化规律基本一致。而由于参数大小选择不同等因素，不同模型的预测结果间也存在明显差异。特别是Liu-Li 模型使用了基于非迭代海-气通量算法的物理和参数化方案来计算蒸发波导高度，即使在统一的气象海洋环境条件中，Liu-Li 模型给出的波导高度也会与其他模型计算得到的波导高度存在或多或少的差异，但Liu-Li 模型在不同海域蒸发波导的诊断上都能较好地进行反应，有些条件下更优于其他模型的诊断效果。

Liu-Li 模型采用了非迭代海-气通量算法，在模型建立上更为高效合理，其预测诊断效果能达到主流模型的水平，能有效地进行蒸发波导诊断预报，尤其在不稳定海气层结状态下结果更为可靠。本研究初步探讨了Liu-Li 模型在不同海域的适应性，在后续研究中还将深入结合模型建立方法与蒸发波导形成机制，拓展其在极端条件下的适用性。