面向不平衡数据的三支决策混合采样算法研究

陈丽芳,代琪,刘洋,刘保相

(1.华北理工大学 理学院,河北 唐山 063210;2.中国石油大学(北京) 自动化系,北京 102249)

0 引言

不平衡数据普遍存在于生活的各个领域。由于不平衡数据集中类间数量不均衡,从这些数据中进行分类学习需要新的算法及工具,以便从原始数据中有效获取有价值信息[1-2]。因此,针对不平衡数据的分类问题,常见的处理方法分为两类:一类是从数据层面出发,对训练集进行重采样;另一类则是在不改变数据集分布的前提下,对分类算法进行改进,增强算法对不平衡数据结构的适应能力,提升算法的分类精度。在实际应用中,数据采样技术因其计算量小,提升效果明显而备受关注,主要分为欠采样、过采样和混合采样。

欠采样的基本思想是通过删除一部分多数类样本,使数据集实现再平衡。其中,随机欠采样[3]是欠采样技术中简单易行的方法,虽然该方法具有操作简单、易实现等优点,但删除过程中容易删除多数类有价值样本,造成信息丢失,算法分类精度提升不明显。Sun等[4]将Bagging算法引入欠采样EUS方法中,提出新的欠采样算法EUS-Bag。Kang[5]等指出少数类样本中可能存在噪声,降低分类器分类性能,从而提出一种结合噪声滤波器的欠采样算法。魏力[6]等结合NearMiss算法和K-means聚类算法的优点,通过计算聚类簇中心点之间的NearMiss距离,对聚类中心赋予不同的选择权重,提出一种新的欠采样算法。

过采样主要是在多数类与少数类之间生成一部分少数类样本的人造数据,实现数据的再平衡。合成少数类过采样技术(Synthetic Minority Oversampling Technique, SMOTE)算法是过采样算法中的经典算法,可以有效地提升过采样方法的性能。夏英等[7]通过层次聚类将少数类样本划分为多个类簇并计算簇的密度因子,获得采样比例,根据每个簇中样本与多数类边界的聚类确定采样权重,从而实现数据集过采样。Rivera[8]在SMOTE的基础上,结合降噪技术,提出一种新的过采样算法,通过减少少数类样本噪声,对少数类样本进行选择性过采样,从而改善少数类样本的分类难度。

混合采样是通过联合欠采样和过采样方法,结合两种或两种以上的采样方法,实现数据的再平衡。吴艺凡等[9]利用SVM的分类超平面划分数据集,对靠近超平面的少数类样本采用SMOTE过采样,删除远离超平面的一些多数类样本,使分类超平面向真实分类边界偏移。Zhang等[10]结合EUS和Boosting算法,结合欠采样和过采样的优势,提出一种有监督的混合采样算法,提高弱分类器的准确率。Liu等[11]将SMOTE与Tomek-Link算法结合,提出新的混合采样算法,首先利用SMOTE对数据进行过采样,然后使用Tomek-Link算法剔除边界域中的样本,从而提升模型的分类精度。

分析以上研究成果,数据采样技术能有效提高不平衡数据的分类准确率,但数据采样过程存在一定的盲目性,使采样算法的计算过程烦琐,鉴于此,本文将三支决策和粒计算思想融入混合采样中,提出一种基于三支等价粒的混合采样算法(Three Equivalent Granules Hybrid Sampling Algorithms,3EG-HS),大大约简了采样计算过程。具体思路如下:采用二元关系粒化数据集,生成正等价粒、不确定等价粒和负等价粒;使用马氏距离分别计算各负等价粒中样本之间的距离,保留距离最小的样本;利用SMOTE算法对不确定等价粒中的少数类样本进行过采样,降低训练集(Imbalanced Ratio,IR)不平衡比。实验结果表明,与其他采样算法对比,该混合采样算法的G-mean值提升效果明显,在不平衡数据分类问题上具有明显优势。

本文的主要贡献如下:

(1)结合三支决策和二元关系,针对不平衡数据提出了三支等价粒概念。

(2)提出的混合采样算法对不同的等价关系采用不同的处理方法,有效地提高了采样准确率,有利于后续分类模型的分类学习。

1 理论知识

本节简要介绍了三支决策、二元关系的理论知识,定义了三支等价粒。

1.1 三支决策

三支决策(Three-way decisions,3WD)是近几年发展起来的一种符合人类认知的“三分而治”模型[12]。三支决策的核心思想是将一个统一集合划分为三个两两互不相交的成对区域,对每一个区域制定相应的决策策略[13]。

定义1(三支决策)[14-15]基于条件集C,三支决策通过一个映射f将对象集U分为三个两两互不相交的R1域、R2域和R3域,即:

f:U→{R1,R2,R3} ,

(1)

其中,R1,R2,R3⊆U,U=R1∪R2∪R3,R1∩R2=ø,R2∩R3=ø,R1∩R3=ø。

特别地,R1域、R2域和R3域可能为空集。若三个区域存在当且仅当一个区域为空集时,三支决策转化为二支决策问题。

1.2 二元关系

定义2(等价粒化)[16-17]令U={x1,x2,…,xn}是一个论域,R是U上的一个二元关系。若R是自反、对称的及传递的,则称R为等价关系。用等价关系实现的粒化,称为等价粒化。

定义3(二元关系)[16-17]设R和S是U上的两个二元关系,定义:

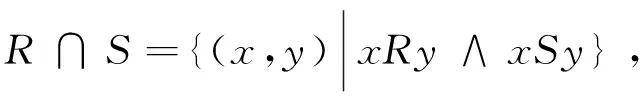
(2)

(3)

式(2)为二元关系的交运算;式(3)为二元关系的并运算。

本文分别使用两个关系R和S获得粒化后的新粒,应用二元关系的交运算对合并后的粒进行细化计算,得到细化后的粒及粒层,新粒分别包含旧粒的所有信息。

1.3 三支等价粒

定义4(三支等价粒)考虑一个二分类问题U,C={C1,C2},其中C1为正类,而C2为负类。假设存在属性a1,a1∈A,通过二元关系粒化,形成等价粒R,如果x1,x2∈R,当x1,x2∈C1时,称该等价粒为正等价粒;当x1∈C1,x2∈C2时,则称该等价粒为不确定等价粒;当x1,x2∈C2时,称该等价粒为负等价粒。

2 算法设计与模型构建

在本节中,主要介绍三支等价粒混合采样算法的算法设计和模型构建过程。其中,2.1节给出了算法设计流程及流程图。2.2节介绍了混合采样分类模型的构建过程。

2.1 算法设计

该算法(Three Equivalent Granules Hybrid Sampling Algorithms,3EG-HS)流程图如图1所示。

图1 三支等价粒混合采样算法流程图Fig.1 Flow chart of three equivalengranules hybrid sampling algorithms

算法步骤如下:

Step1:数据归一化处理

由于样本集初始属性表中各属性之间量纲不同、取值范围不同,原始数据差异较大。为了避免计算过程产生误差,采用比例转换法、极差转换法等方法,消除量纲和取值范围的影响,将属性值规范到一定区间上,使属性之间能够进行比较。

Step2:数据离散化处理

每个属性设置相同或不同的区间,采用等距划分方法对归一化后的数据进行离散化处理。

Step3:等价类划分

采用二元关系计算实现属性粒化处理,得到最终等价类。

Step4:三支等价粒粒化

根据Step 3粒化形成的等价粒,采用三支决策思想划分为正等价粒、不确定等价粒和负等价粒。当粒中样本均为少数类时,划分为正等价粒;当粒中样本包含多数类样本及少数类样本,划分为不确定等价粒;当粒中样本均为多数类时,划分为负等价粒。

Step5:负等价粒欠采样

负等价粒主要包含大量的多数类样本,在多数类样本中也可能存在有价值样本,完全删除负等价粒可能导致分类器性能降低,因此,当负等价粒中只包含唯一样本时,该样本直接保存,当负等价粒中包含多个样本时,采用马氏距离计算负等价粒中各样本与等价粒中其他样本之间的距离,保留距离最小的样本,合并所有保留的负等价粒样本形成新的欠采样样本集。

Step6:不确定等价粒过采样

不确定等价粒中包含少数类样本和多数类样本,这些样本不容易区分,因此,采用SMOTE算法对整个不确定粒层进行过采样,形成新的过采样不确定等价粒,其采样过程如下。

首先,随机选择少数类样本,并根据公式(4)计算样本之间的欧氏距离。假设存在两个相同维度的样本X={x1,x2,…,xn},Y={y1,y2,…,yn},那么样本X与样本Y的欧氏距离为:

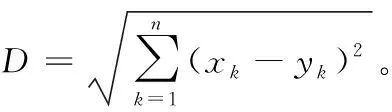
(4)

然后,计算不确定等价粒层上少数类样本与多数类样本的比例,获得过采样比例及生成人工数据点的数量。

最后,通过在少数类样本中随机选择样本点,与其k个最近邻样本之间线性内插合成新的少数类样本,根据公式(5)合成新的数据样本。

xnew=xi+rand(0,1)×(xi,j-xi) ,

(5)

其中,xnew为新的少数类样本,xi为第i个少数类样本,xi,j为第i个少数类样本的第j个近邻样本。

Step 7:合并三支等价粒

采用两两相互组合的方式合并正等价粒、过采样不确定等价粒和欠采样负等价粒,形成新的采样数据集。

计算中有两点需注意:第一,不确定等价粒包含更多重要信息,需采用过采样方法进行二次处理;第二,若完全删除负等价粒,容易丢失有价值的多数类样本,导致分类器性能降低,因此采用马氏距离计算负等价粒中各样本的距离,保留各等价粒中距离最小的样本,当负等价粒中只存在一个样本时,不再对样本计算马氏距离,直接将该负等价粒保留。

2.2 模型构建

经过以上混合采样算法,可以获得相对平衡的新训练集,分别在新训练集上构建分类器,并对分类结果进行对比分析,验证算法的准确性及可行性。

模型构建的具体步骤如下:

步骤1:按照80%训练集Strain,20%测试集Stest的比例划分原始数据集S,在训练过程中采用五折交叉验证评估模型的稳定性。

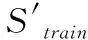
步骤3:使用测试集中的数据测试模型的分类精度,并使用G-mean值计算模型的得分,计算公式如下所示。

(6)

其中,TP为少数类样本正确分类数;FN为少数类样本错误分类数;FP为多数类样本错误分类数;TN为多数类样本正确分类数。

3 仿真实验与性能分析

本节主要介绍了算法示例、数据集及仿真环境和分类算法的性能分析。

3.1 算法示例

以KEEL数据库中haberman数据集中的部分数据(20个样本)为例,给出计算过程,原始数据如表1所示。

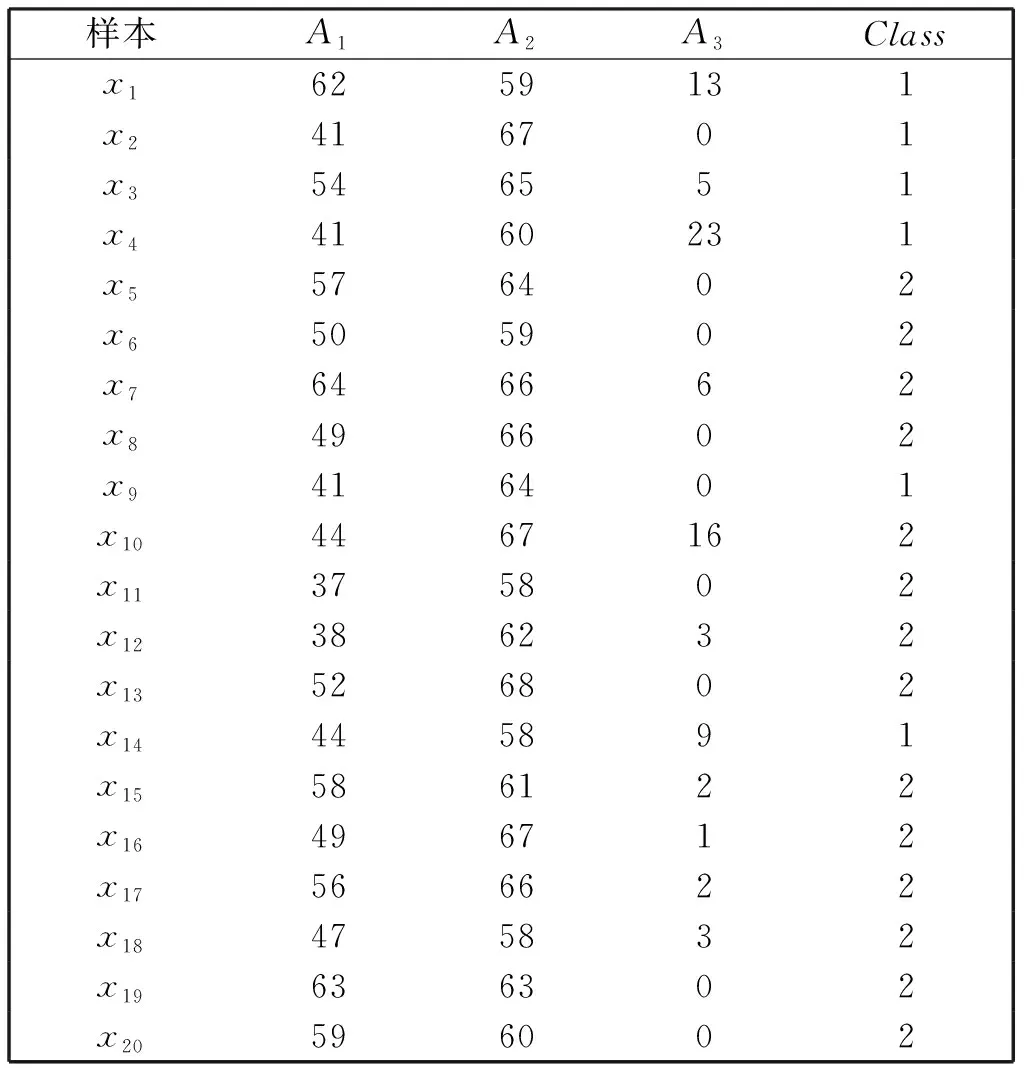
表1 haberman部分真实数据

根据公式(7)归一化数据集,采用等距划分方法对数据离散化为3类,由于篇幅所限,此处省略离散化后的属性表。

(7)

利用二元关系粒化形成三支等价粒。选择属性A1作为等价粒层R进行计算,可以将论域U粒化为3类,分别为:

选择属性A2作为等价粒层S进行计算,可以将论域U粒化为3类,分别为:

粒化获得8个等价粒,其余交运算结果均为ø。

依据算法计算过程,本数据集类别为1的是少数类,因此,三支等价粒划分如下:

仅包含少数类样本的等价粒定义为正等价粒,划分结束后,正等价粒为:ø;

既包含类别1又包含类别2的等价粒定义为不确定等价粒,划分结束后,不确定等价粒为:{x4,x11,x14},{x9,x12},{x2,x10},{x3,x8,x13,x16},{x2,x10},{x3,x8,x13,x16},{x1,x15,x20};

只包含类别2的等价粒定义为负等价粒,划分结束后,负等价粒为:{x6,x18},{x5,x19},{x7,x17}。

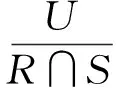
具体计算过程此处不再赘述,按照此方法,确定数据集的正等价粒、不确定等价粒、负等价粒。

三支等价粒划分后,对各负等价粒分别采用马氏距离计算并查找待合并样本;对不确定等价粒合并后使用SMOTE算法进行过采样。经仿真实验,合并不确定等价粒统一进行过采样,能够提升运算效率,节省计算时间,因此本文采用合并的方法对不确定等价粒进行计算。

3.2 数据集及仿真环境

基于Python编程实现算法仿真。系统环境如下:

硬件环境:CPU:i3-2348M;RAM:8 GB;

软件环境:操作系统:Windows 10专业版;解释器:Python 3.7。

该算法(3EG-HS)使用KEEL不平衡数据库中的20组数据集进行仿真实验,数据集基本信息如表2所示,其中“不平衡比”表示数据集中多数类样本与少数类样本的数量比值。

3.3 性能分析

仿真过程中,该算法(3EG-HS)分别与ENN、ADASYN[18]、SMOTE[19]、SMOTE+ENN、SMOTE+TL[20]五种采样算法进行对比实验,选择CART、ELM和SVM作为模型的基分类器,验证模型的分类性能,以G-mean、F-measure1计算模型的最终得分。

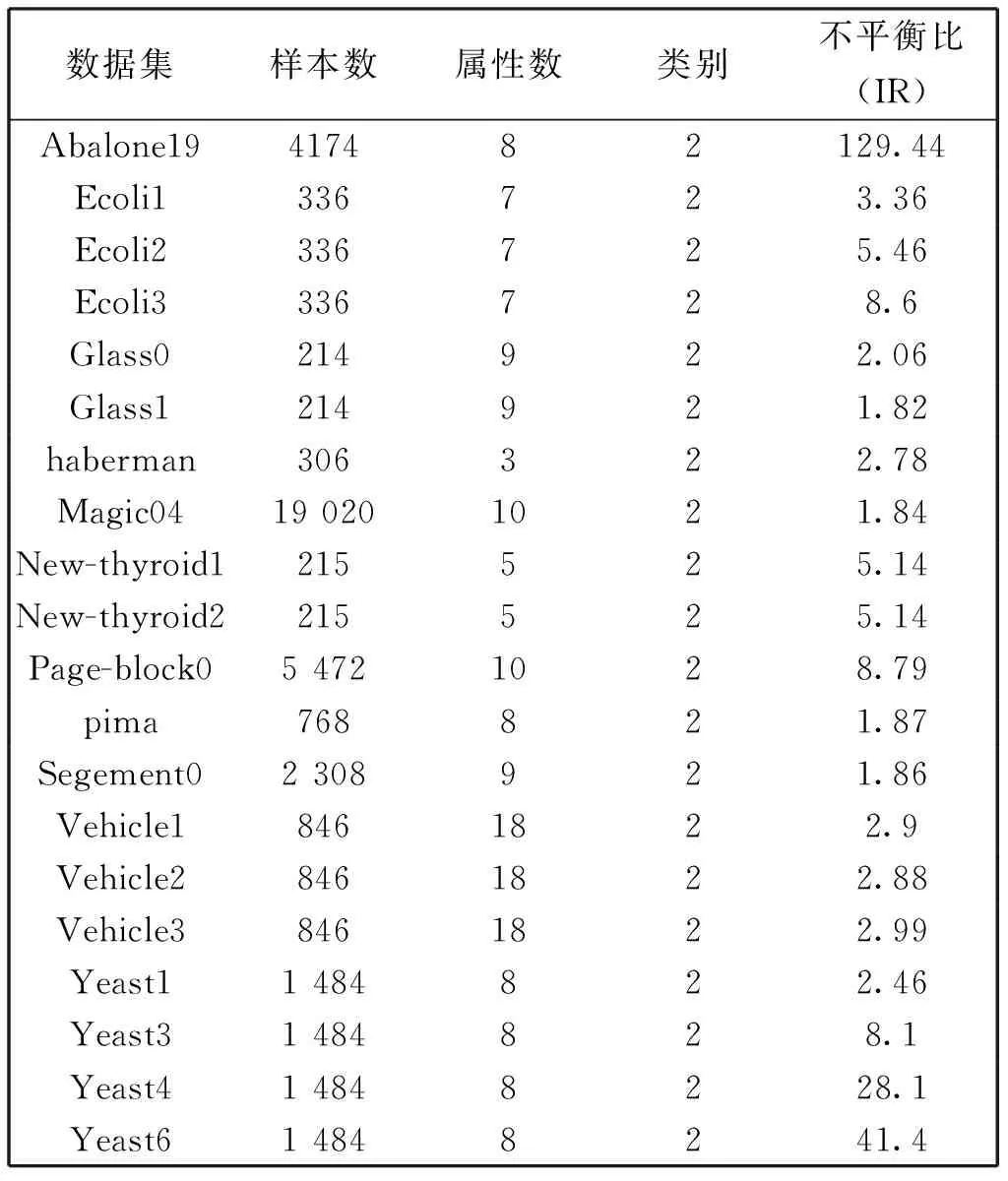
表2 数据集基本信息

原始数据集按照80%训练集,20%测试集的比例划分,采用五折交叉验证的方式计算分类模型的标准差验证模型的稳定性,算法标准差越低,模型稳定性越好,反之,稳定性差。各模型的G-mean值如表3所示,最优结果均以加粗的形式在表格中标出。

根据表3中各模型的G-mean值结果可以看出,该混合采样算法(3EG-HS)在大部分数据集上具有明显的分类优势,其中在abalone19、ecoli2、ecoli3、new-thyroid1、newthyroid2、pima、yeast3、yeast6八个数据类SVM具有更优秀的分类性能;在ecoli1、glass0、haberman、page-blocks0、segment0、vehicle2六个数据集上CART决策树分类精度提升明显;在glass1上ELM的分类性能优于其他分类模型,在其他数据集上,ELM的分类性能欠佳,不能有效地识别少数类样本。ELM是单隐层前馈神经网络,在训练过程中需要随机给定参数,每次训练都会产生不同的训练结果,因此,在选择ELM作为基分类器时,更重要的是优化模型参数。

在magic04、vehicle1、vehicle3、yeast1、yeast4五个数据集上,3EG-HS的分类性能低于其他分类模型,由于采样前需要将数据进行归一化和离散化处理,归一化方法及离散化取值范围对采样结果影响较大。离散化取值范围的大小与粒化过程中粒的粗细息息相关,当取值范围较细时,粒化形成的等价粒更细,反之,粒化形成的等价粒较粗。

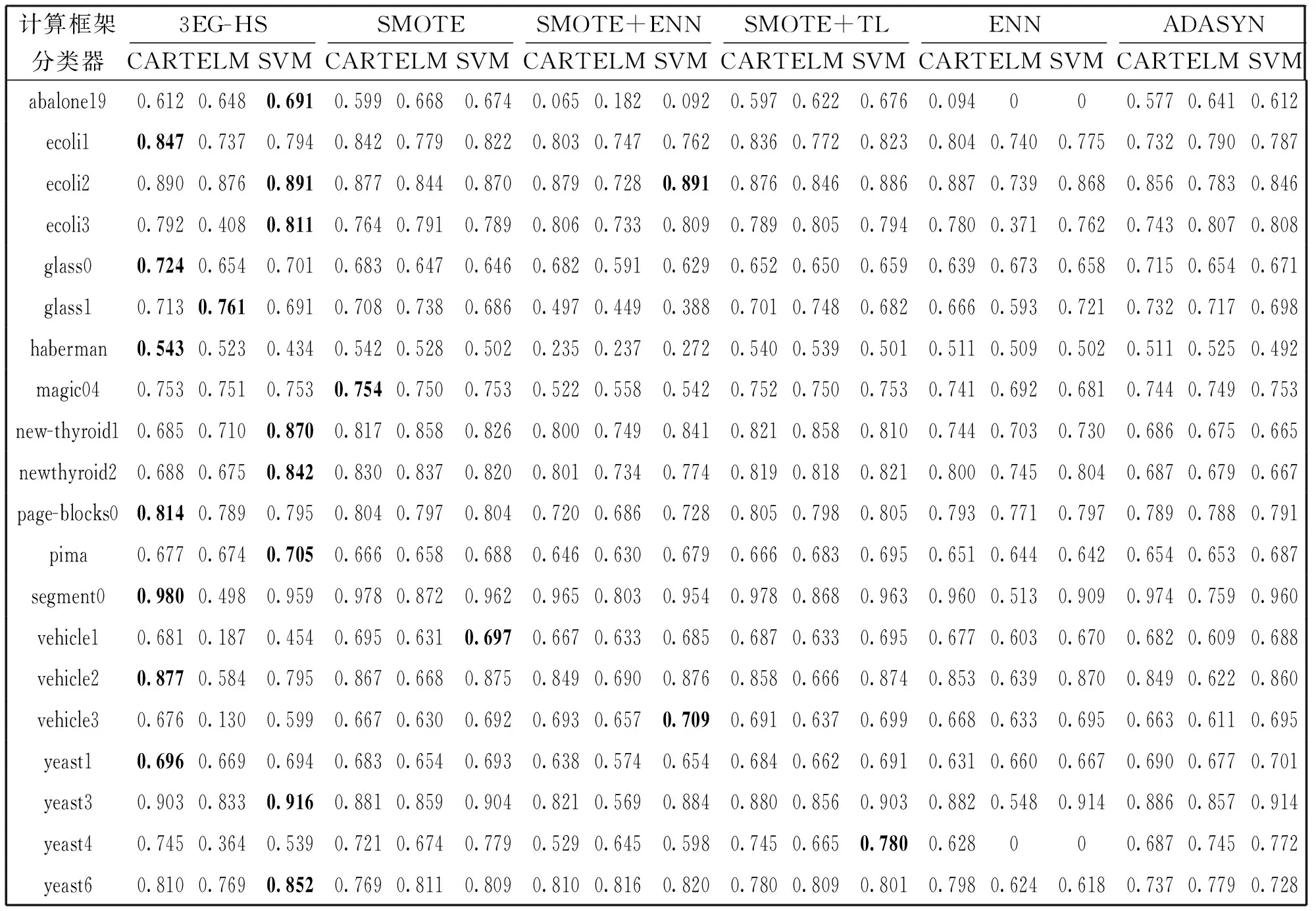
表3 分类模型的G-mean值

图2表示分类模型在不同数据集上G-mean值的均值,分析图中数据可以得出,选择过采样或混合采样技术处理不平衡数据时,训练集中少数类样本与多数类样本数量差距不大,SVM的分类性能优于CART和ELM;选择欠采样处理数据集时,CART表现出更加优秀的分类性能。因此,当选择混合采样或过采样技术对不平衡数据预处理时,可以优先考虑选择SVM作为基分类器,当选择欠采样技术处理不平衡数据时,建议优先考虑决策树,如CART、ID3等决策树。

在不平衡数据分类过程中,不仅需要考虑分类精度,也需要考虑模型的稳定性,采用标准差衡量模型稳定性,分类模型在各数据集上分类标准差的均值如图3所示。

图2 各模型G-mean值均值Fig.2 Mean G-mean value of each model

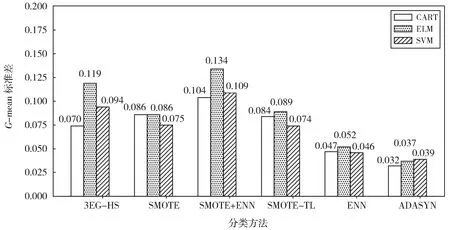
图3 分类模型G-mean值的标准差均值Fig.3 Means of standard deviation of G-mean values of classification models

分析图3中各分类模型G-mean值的标准差均值可以看出,在所有采样算法框架下,ELM的标准差均值最高,SVM次之,CART的标准差均值最低,因此,CART的稳定性优于其他两种分类算法。在3EG-HS混合采样框架下,CART决策树的稳定性优于其他两种混合采样算法。因此,就稳定性而言,CART更具有竞争力。

分析F-measure1值的公式的计算过程可以得出,F-measure1综合了P和R的评价结果,当F-measure1较高时,则分类算法的性能越好,当数据较大时,查准率和召回率却是互相制约的两个评价指标,并不能同时得到最优结果,因此,在不平衡数据处理过程中,不能单独使用查准率或查全率评价模型的分类性能,需要综合分析模型的分类性能。

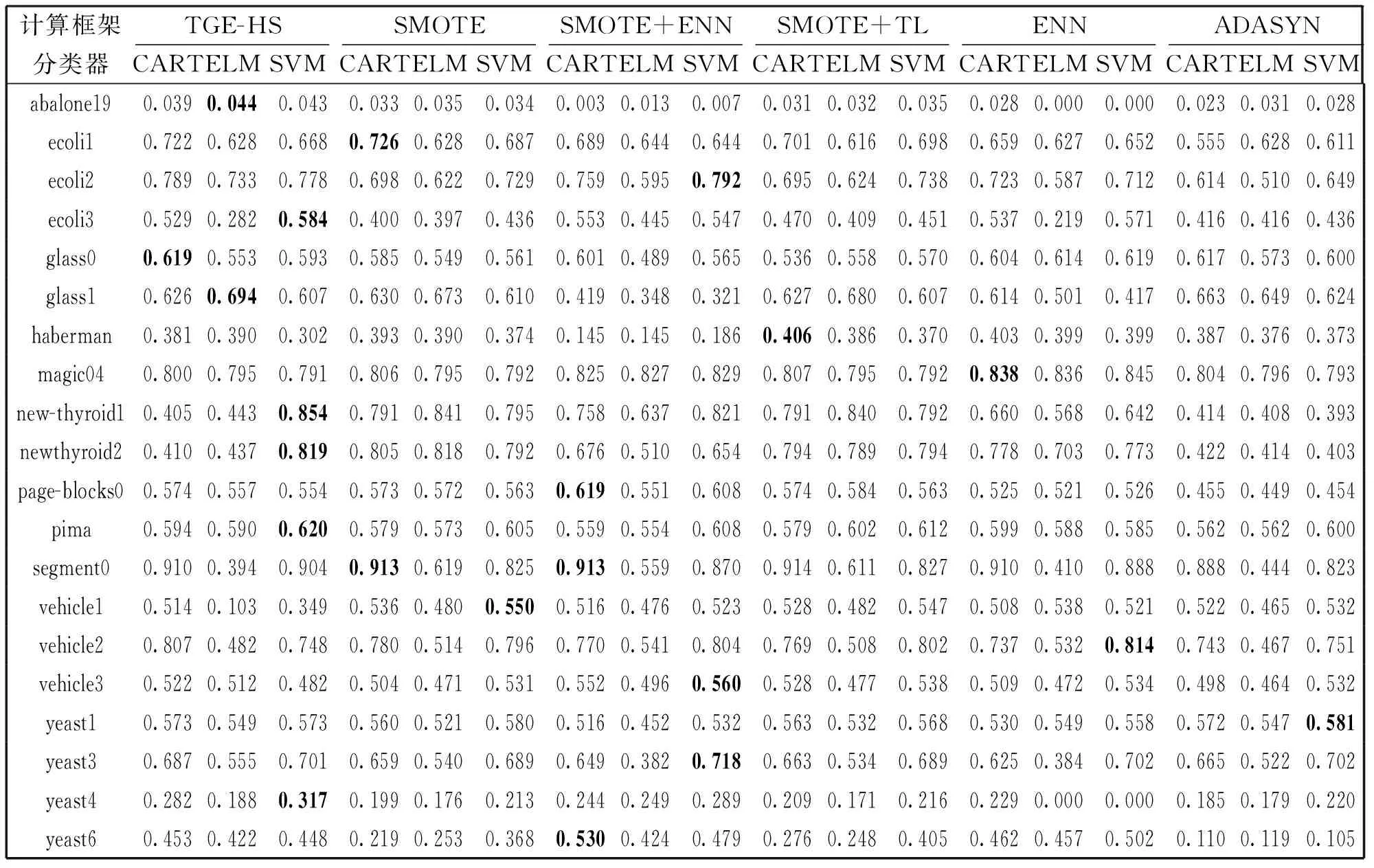
表4 分类模型的F-measure1值

分析表4中各分类模型的F-measure1可以看出,3EG-HS在大部分数据集上性能提升明显,仅仅在haberman、page-blocks0、segment0、vehicle1、vehicle2、vehicle3、yeast1、yeast3、yeast6九个数据集上F-measure1值小于其他分类模型。由于该算法(3EG-HS)在离散过程中存在主观因素的影响,离散化取值范围的选择上不能准确地选择最适宜的离散区间,因此,在采样过程中,对模型的分类性能影响较大。

从图4中可以看出,各模型的F-measure1值相差并不大,分析结果可以看出,SVM的F-measure1值大于CART和ELM,而ELM的F-measure1值最低。因此,当采用F-measure1作为评价标准,且需要更高的F-measure1时,建议优先选择SVM作为基分类器,而采样方法并没有明显的差异性,对于3EG-HS混合采样方法优化归一化方法和离散化区间有利于提高模型的分类性能。

图5中展示了在不同采样框架下F-measure1值标准差的平均值,ADASYN和ENN的总体标准差均值优于其他分类模型,而在混合采样模型中,CART的稳定性优于其他两种混合采样模型,而SVM和ELM的稳定性仍然属于次优。

由图6可以看出,3EG-HS算法在运算时间上略低于SMOTE算法,其主要原因是在过采样的同时还需要对数据集进行欠采样,造成该算法的训练时间略长于SMOTE算法。SMOTE+ENN和SMOTE+TL两种混合采样算法均是先对数据集进行过采样,然后使用ENN和TL算法剔除边界域中的样本,而3EG-HS混合采样算法是对数据进行预处理后,将不同的数据分别进行欠采样和过采样,因此,该算法与SOMTE+ENN和SMOTE+TL两种混合采样算法相比,运算时间明显缩短。

图4 分类模型的F-measure1值均值Fig.4 Mean F-measure1 values of the classification models

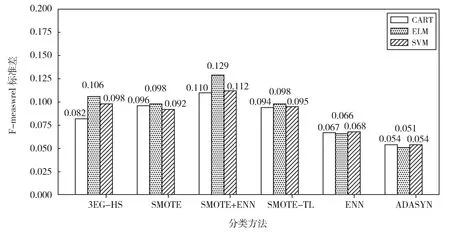
图5 分类模型F-measure1值标准差均值Fig.5 Mean values of standard deviation of F-measure1 values of classification models

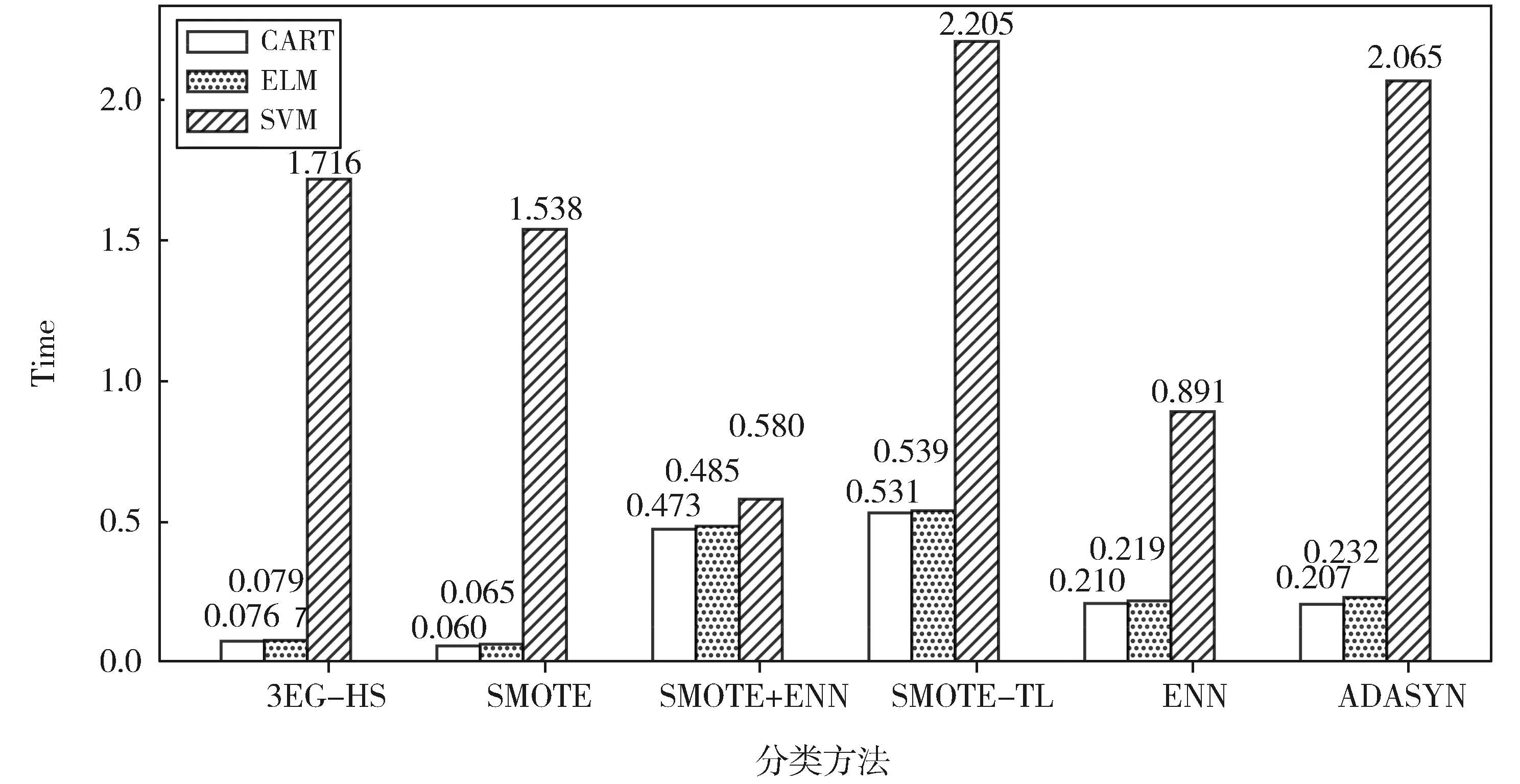
图6 分类模型运行时间均值Fig.6 Mean running time of classification models

4 结论

混合采样算法是处理不平衡数据的常用方法,传统的混合采样方法采用串联的方式处理训练集,容易造成模型分类精度偏低,计算时间过长的问题。本文提出的混合采样算法,以三支决策为理论依据,使用二元关系将数据集划分为正等价粒、不确定等价粒和负等价粒,对不同等价粒上的数据采用不同的采样方法。实验结果表明,该算法与较新的采样算法相比,大部分数据集上,分类精度提升效果明显,大幅缩短了模型的运算时间,为不平衡数据采样算法的研究提供了新的思路。