联合邻域边界的在线流特征选择算法
2021-01-08吕彦林耀进陈祥焰李珑珠王晨曦
吕彦,林耀进,陈祥焰,李珑珠,王晨曦
(闽南师范大学 计算机学院 数据科学与智能应用福建省高等学校重点实验室,福建 漳州 363000)
0 引言
在数据挖掘和机器学习分类任务中,特征选择或属性约简是一种有效的数据预处理方法。其主要目的是减少冗余特征,简化分类模型的复杂性,提高分类模型的泛化能力。目前,特征选择广泛应用于医疗诊断[1]、欺诈检测[2]、文本分类[3]和近似推理[4]等领域。传统的特征选择方法假设在进行特征选择前,整个特征空间是已知的。然而,在许多实际应用中,并不是所有的特征都是可以提前获取的。例如,在新浪微博中,热门话题榜单每10 min就会变动1次,当1个新的热门话题出现时,它可能会带有一组新的关键字,而其中一些新关键字可用于识别新热门话题的关键特征[5]。在大数据时代,数据呈现高维海量特点及整体特征空间无法提前获取的情况下,在线流特征选择技术具有极其重要的实际应用价值。
近年来,针对流环境下的在线特征选择算法备受研究者的关注[6]。在线流特征选择方法是按所有的备选特征动态生成,即随着时间的推移特点一个接一个流进来。目前,在线流特征选择算法可分为单标记流特征和多标记流特征选择,一些代表性的单标记在线流特征选择算法被先后提出,其中Perkins和Theiler[7]提出分段梯度下降的在线特征选择算法Grafting。Wu等[8]提出了一种在线流特征选择的基本框架,并介绍了两种可快速选择强相关和非冗余特征的在线流特征选择算法(Online Streaming Feature Selection,OSFS)和快速在线特征选择算法(Faster Online Streaming Feature Selection,Fast-OSFS)。Yu等[5]提出采用在线成对比较方法处理高维数据的可伸缩性算法(Scalable and Accurate Online Feature Selection Approach,SAOLA)。考虑传统邻域粗糙集方法都需要预先指定一些参数,Zhou等[9]改进邻域粗糙集模型,设计了一种基于自适应密度邻域关系的在线流特征选择新算法(A New Online Streaming Feature Selection Method Based on Adaptive Density Neighborhood Relation, OFS-Density)。
上述在线流特征选择算法仅适用于处理单标记数据问题。对于多标记学习,代表性的多标记流特征选择算法包括Lin等[10]采用模糊互信息来评估多标签学习中特征的质量,并提出了一种多标记流特征选择算法(Multilabel Streaming Feature Selection,MSFS)用于处理特征空间完全已知或部分已知时的场景。Liu等[11]基于邻域粗糙集提出了一种新颖的在线多标记流特征选择算法(Online Multi-label Streaming Feature Selection Based on Neighborhood Rough Set,OMNRS),用于选择包含高度相关且非冗余特征的特征子集。
然而,上述基于邻域粗糙集的流特征选择算法在计算属性依赖度时,仅考虑条件属性子集的正域中包含的信息,而忽视了边界区域中包含的信息。与正域不同,边界区域内的样本包含同类样本与异类样本,故而可将边界样本看作是含有噪声的正域。因此降低边界区域中噪声样本的影响,并将其与邻域粗糙集中的依赖度结合使用,可以更好地限定特征子集之间的依存关系。由此,本文改进了邻域粗糙集模型依赖度的计算方法,提出了一种联合邻域边界的在线流特征选择算法(Joint Neighborhood Boundary for Online Streaming Feature Selection, OFS-JNB)。OFS-JNB根据“在线依赖度分析、在线重要度分析和在线冗余度分析”三大评估准则,在线依次处理流进特征空间的特征,从而所选特征子集与决策属性表现出高依赖性、高重要度和低冗余性。最后,在具有不同应用场景的8个数据集上进行的实验证明,该算法所选出的特征子集,能够有效提高分类效率。
1 邻域粗糙集
定义1[12]给定一个非空有限样本集合U={x1,x2,…,xn},C={a1,a2,…,am}作为描述论域U的实数型特征集合,如果C能生成该论域U上的一簇邻域关系,D为决策属性,则称NDS=〈U,C,D〉为邻域决策系统。
定义2[12]给定非空的有限样本集合U={x1,x2,…,xn},对∀xi∈U的邻域δ(xi)可定义为
δ(xi)={xj|Δ(xi,xj)≤δ,xj∈U}。
xi的邻域δ(xi)是以xi为中心,δ为半径的球体。
定义3[12]给定邻域决策系统NDS=〈U,C,D〉,D将U划分为N个等价类{X1,X2,…,X},B⊆C生成U上的邻域关系RB,则决策属性D关于条件属性子集B的下近似和上近似分别为
其中
NDS的正域和负域分别定义为
定义4[12]给定邻域决策系统NDS=〈U,C,D〉,B⊆C,决策属性D对于条件属性子集B的依赖度为
由上式可知依赖度是单调递增的,若
B1⊆B2⊆…⊆C,
则有
γB1(D)≤γB2(D)≤…≤γC(D)。
定义5[12]给定邻域决策系统NDS=〈U,C,D〉,若B⊆C满足以下条件,则B是C的一个约简
1)∀a∈B,γB-a(D)<γB(D),
2)γB(D)=γC(D)。
即约简后的集合中,所有的属性都应该是必不可少的,且不存在冗余的属性;同时,属性约简是在不降低系统的区分能力下的约简。
定义6[12]给定邻域决策系统NDS=〈U,C,D〉,B⊆C,对∀a∉B,条件属性a的重要度定义如下
sig(a,B,D)=γB∪a(D)-γB(D)。
2 联合邻域边界的在线流特征选择算法
本文重点研究了传统基于邻域粗糙集的在线特征选择在计算条件属性集合的依赖度时,忽视了边界区域中包含的信息的问题。首先对邻域粗糙集理论进行扩展,介绍了一种计算条件属性集合依赖度的新方法。并在此基础上,提出了三种在线选择特征的评估准则,用于选择与决策属性依赖度高,同时特征间冗余度低的特征子集。
2.1 邻域粗糙集的扩展
传统方法通过对不同类型数据设置不同的阈值,致使存在粒度选择问题[11]。为了使所有实例粒度化,同时避免粒度选择的问题,引入最大近邻的方法来设置信息粒子的大小。同时,传统基于邻域粗糙集的特征选择算法仅利用条件属性集合的正域来计算依赖度,而忽略了边界区域的重要性。在大多数情况下,数据分布往往是不均匀的,上近似与下近似的集合大小差别较大,即边界区域包含较多样本。然而这些样本中包含的大量有用信息被噪声所影响,使得依赖度的计算有一定的不足。由此,本文引入边界区域,对原始邻域粗糙集理论进行扩展,提出一种计算属性依赖度的新方法。
定义7 给定一个邻域决策系统NDS=〈U,C,D〉,x∈U的邻域为
δ′(x)={y|Δ(x,y)≤d(x),y∈U},
(1)
其中
d(x)=max(d1(x),d2(x)),
d1(x)=Δ(x,NM(x)),
d2(x)=Δ(x,NH(x)),
其中,NH(x)是样本x的最近同类样本,NM(x)是样本x的最近异类样本。Δ(x,NM(x))与Δ(x,NH(x))分别表示样本x到NM(x)和NH(x)的距离。
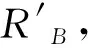
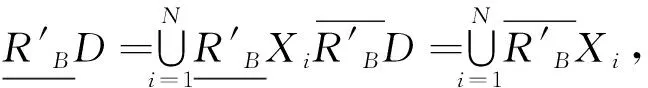
(2)
其中
NDS的正域和边界分别定义为
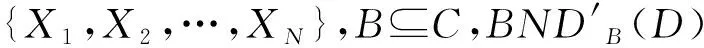
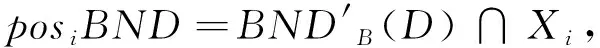
(3)
相对正域posiBND的权重定义为
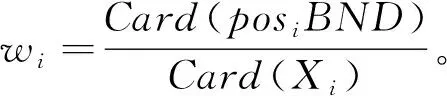
(4)
定义10 给定邻域决策系统NDS=〈U,C,D〉,B⊆C。若使权重集合w={w1,w2,…,wN}的最大值大于0.5,则决策属性D对于条件属性子集B的依赖度为
s.t.wi≥0.5,wi=max(w)。
(5)
否则,决策属性D对于条件属性子集B的依赖度为
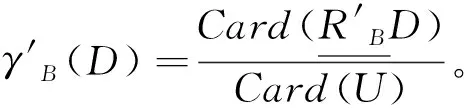
(6)
定义11 给定邻域决策系统NDS=〈U,C,D〉,B⊆C,对∀a∉B,条件属性a的重要度定义如下
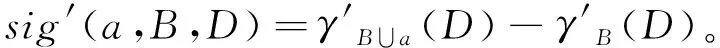
(7)
基于公式(5)和公式(6),提出了一种联合邻域边界的依赖度计算方法(Dependency of Joint Neighborhood Boundariy,DJNB)。
2.2 DJNB算法

DJNB算法输入:NDS=
在DJNB算法中,返回的是特征子集B的依赖度。在DJNB算法中,步骤7-8是计算边界区域相对于类别集合Xi的相对正域posiBND,并计算相对正域的权重wi。步骤10-14是计算依赖度。若权重集合w的最大值大于等于0.5,则意味着,边界区域内样本与相应类别集合内的大部分样本分布一致,则根据公式(5)计算条件属性集合的依赖度。若权重集合w的最大值小于0.5,则根据公式(6)计算条件属性集合的依赖度。若假设|U|是训练样本的数目,那么算法的时间复杂度为O(|U|·log|U|)。
2.3 三种在线评估准则
与传统的特征选择方法不同,基于特征流的在线特征选择随着时间的推移,逐个获取特征,同时必须快速决定对在t时刻新到达的特征ft是保留还是丢弃[13]。由此,三种评估特征子集的准则被提出。具体内容如下:
1) 在线依赖度分析(Online dependence analysis)
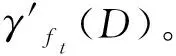
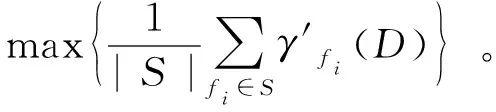
(8)
使用“在线依赖度分析”准则来选择依赖度高的特征,同时依赖度低的特征将不做考虑,但是它所筛选的子集中存在冗余特征。
2) 在线重要度分析(Online importance analysis)
已知邻域决策系统NDS=〈U,C,D〉,其中C={f1,f2,…,ft},特征ft相对于决策属性D的重要度定义为
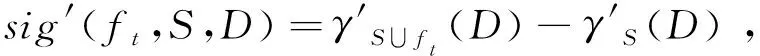
(9)
其中,ft为t时刻新到达的特征,S⊆C是当前时刻下已选的特征子集。在线重要度分析可以有效地评估当前特征ft的重要性,若特征ft的重要度大于0,则ft被认为是对决策属性有效的特征,此时应该保留该特征,否则ft被认为是一个没有意义的特征,将不被考虑。
3) 在线冗余度分析(Online redundancy analysis)
给定邻域决策系统NDS=〈U,C,D〉,其中条件属性集合C={f1,f2,…,ft},S⊆C为已选特征子集,ft为t时刻新到达的新特征。若∃S′∈S,满足公式(10),则将ft添加到S′中,进而取代特征子集S。
(10)
2.4 OFS-JNB算法
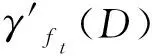
如果ft满足“最大依赖度准则”,步骤8判断特征ft的重要性,若ft∪S的依赖度大于S的依赖度,则将特征ft添加进特征子集S中。
步骤11至16是“在线冗余度分析”,用于检查S中是否存在与ft是相互冗余的特征。步骤12-15,评估ft是否应该被添加进当前已选特征子集S,如果∃fi∈S满足公式(10),则应该将ft添加入S中,而将fi从已选特征子集S中删除。

OFS-JNB算法输入:NDS=
由此,根据三种在线评估准则的约束,我们能够选择出高依赖性、高重要度和低冗余度的特征子集。
2.5 时间复杂度分析
本文算法主要是选择与决策属性依赖度高,同时特征间冗余度低的特征子集。在t时刻,|S|是当前已选特征子集中特征的个数,D为决策属性,U为论域。在最好的情况下,OFS-JNB算法通过“在线依赖度分析”准则已经可以获得了一个好的特征子集,这一步骤的时间复杂度为O(|U|·log|U|)。然而OFS-JNB算法在很多情况下,并不能如此简单就能获得最好的特征子集,所以必须要通过“在线重要度分析”准则和“在线冗余度分析”准则进一步筛选。“在线重要度分析”和“在线冗余度分析”的时间复杂度取决于比较决策属性分别对已选特征子集和候选特征子集的依赖度。所以,在最坏情况下,我们需要对每一个当前时刻流进来的特征进行“在线冗余度分析”处理,其时间复杂度为O(|S|·|U|2·log|U|)。但在实际应用情况下,“在线依赖度分析”准则已删去大多数特征,故该算法真实时间复杂度远小于O(|S|·|U|2·log|U|)。
3 实验及结果分析
3.1 实验数据
实验通过一次处理一个特征的方式来模拟特征流。实验中采用K-近邻(K=3)、分类回归树(CART)和线性支持向量机(LSVM)三种分类器对选定的特征子集进行评估[14]。另外,对每个数据集进行10折交叉验证,9/10的数据样本进行训练,其余1/10数据进行测试。实验平台统一采用Matlab R2013b。本文将OFS-JNB算法在不同数据集上的分类精度和选择特征的数量与最先进的流特征选择算法进行对比。其中数据集包括AUTOVAL_B、CAR、GENE2、GENE4、GENE7、MLL、SRBCT、WARPAR10P(见表1)。
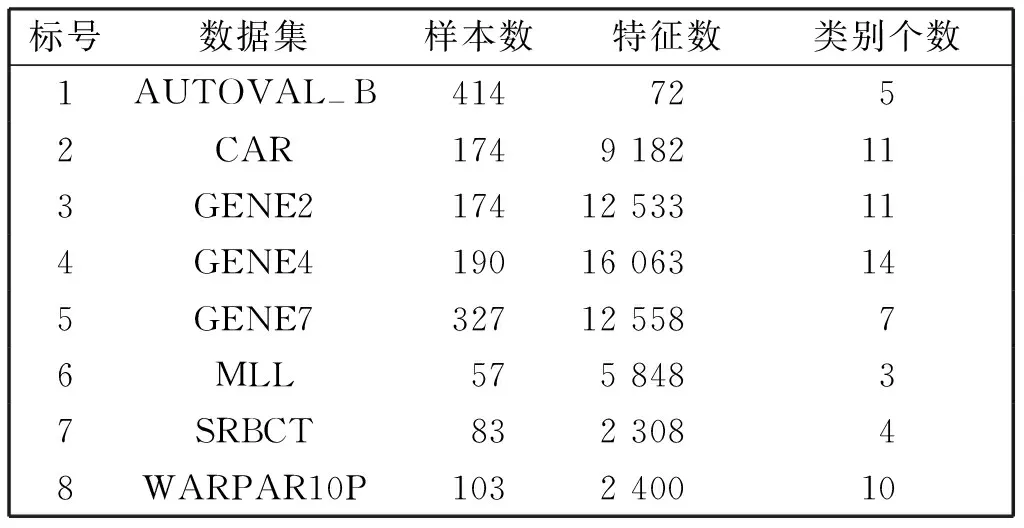
表1 数据集的描述
3.2 结果分析
为了进一步验证OFS-JNB算法的有效性,实验采用OSFS、Fast-OSFS、SAOLA、α-investing[15]和OFS-Density作为对比算法。
OSFS、Fast-OSFS算法动态选择强相关和非冗余特征,包含两个主要步骤:在线相关性分析(丢弃不相关特征)和在线冗余分析(消除冗余特征)[8]。为了解决从超高维数据中在线选择特征的挑战,SAOLA通过对特征之间两两相关的界限进行理论分析,采用了新颖的在线两两比较的技术,并以在线的方式在一段时间内保持一个简单的模型。α-investing是一种基于流回归的自适应复杂度惩罚的流式特征选择方法,它能够动态的调整阈值以减少添加新特征所产生的误差[15]。OFS-Density算法利用周围实例的密度信息提出了一种新的自适应邻域关系,通过使用模糊等式约束进行冗余分析,从而选择冗余度较低的特征。
OFS-JNB不需要预先设定任何阈值。OSFS、Fast-OSFS和SAOLA中显著性水平参数α均设置为0.01,α-investing模型中参数α的设置与文献[15]相同。OFS-Density模型中的参数λ设置为0.05。
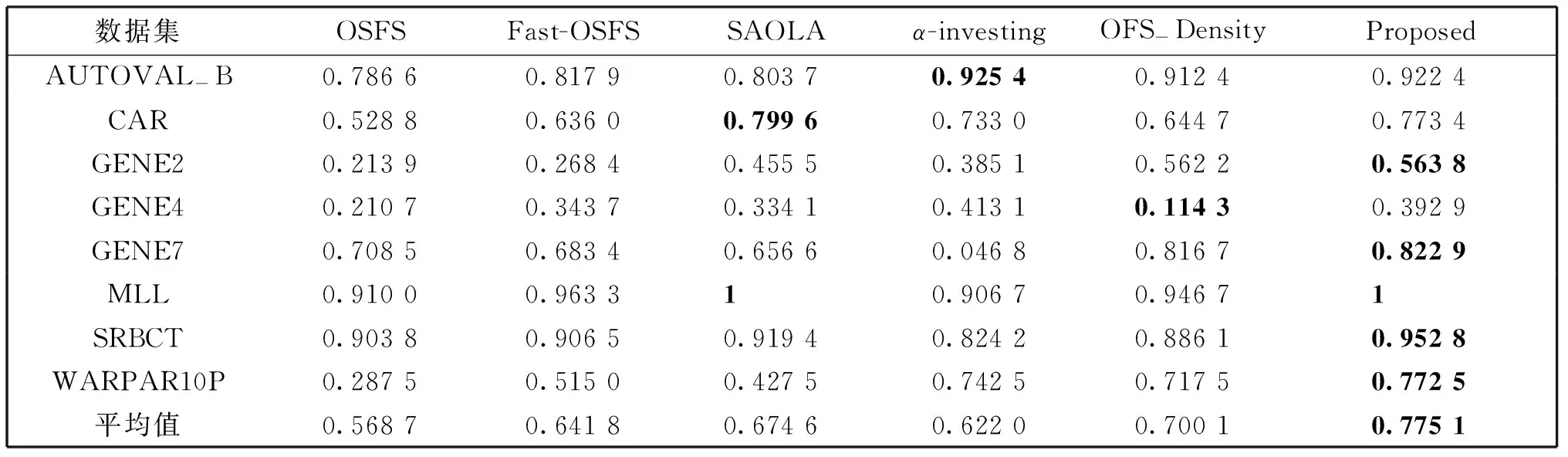
表2 6种算法在KNN分类器上分类精度的对比
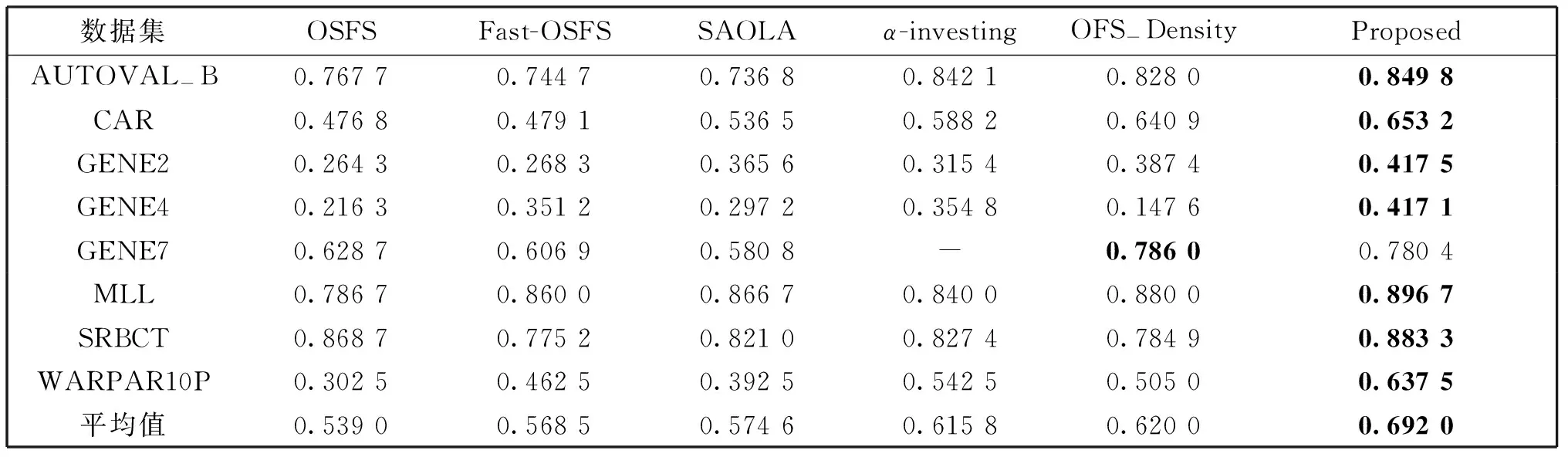
表3 6种算法在CART分类器上分类精度的对比
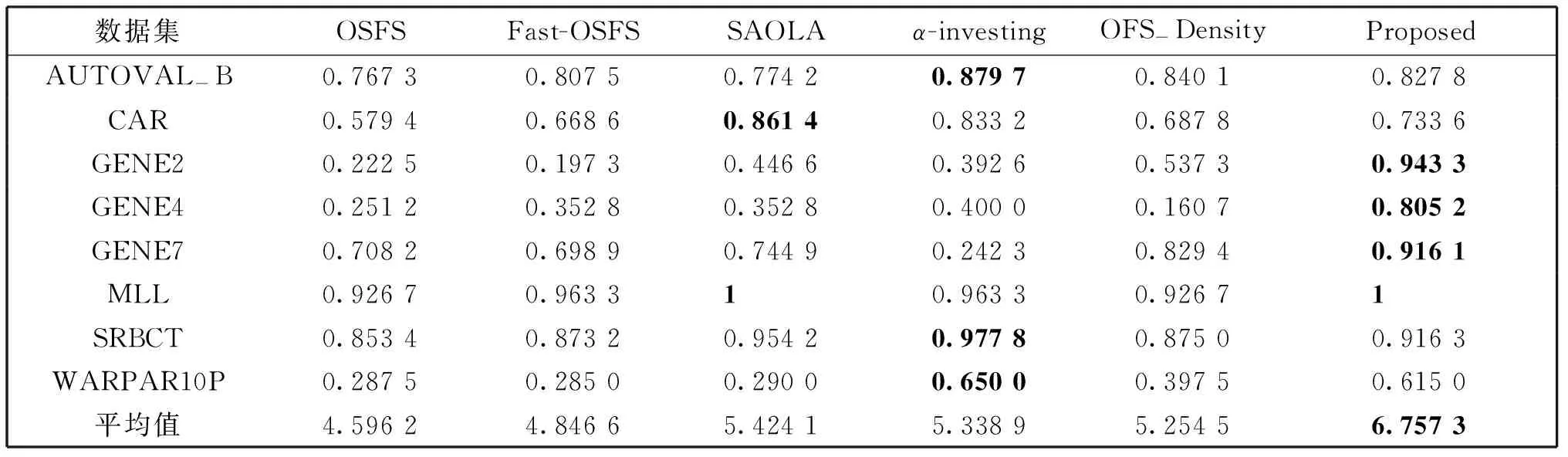
表4 6种算法在LSVM分类器上分类精度的对比
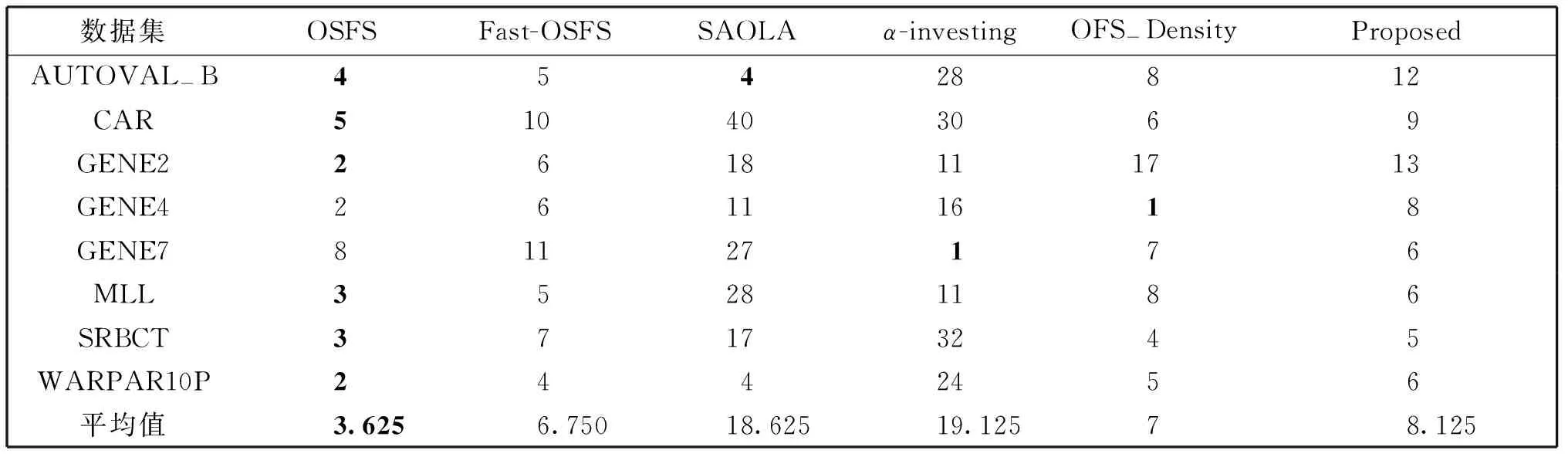
表5 6种算法在8个数据集上选择特征的个数
表2-表4分别描述6种算法在KNN(K=3)、CART和LSVM分类器上的分类精度。表5为6种模型在8个数据集上选择的特征数量。
基于KNN、CART和LSVM分类器,OFS-JNB算法在GENE2和MLL数据集上都优于其他五种对比算法,同时上述其他四种对比算法在这两个数据集上的分类精度都不高。
在GENE4数据集上,采用各类分类器对上述6种算法进行评估时,仅OFS-JNB算法在LSVM分类器上获得了较高的预测精度,其余算法的预测精度均不理想。尤其是OFS-Density算法在各类分类器下预测精度均不足0.2。
由表5可知,OSFS在8个数据集上,均选择了很少的特征,尽管在特征数量上OSFS算法具有非常大的优势,但结合表2-表4可知,OSFS的分类精度也低于其他对比算法。无论是在哪个分类器下,OSFS、Fast-OSFS和SAOLA算法在数据集WARPAR10P上的都很低,只能达到0.3左右,其主要原因是该数据集非常稀疏,这四种算法只能选择这些数据集的后几个特征。
由表2-表5可见,SAOLA和α-investing在CAR数据集上所选特征子集中特征数量远多于其他对比算法,预测精度也高于其他对比算法,然而,其预测精度与对比算法的差异较小。SAOLA在数据集GENE7上所选特征个数远多于其他对比算法,而预测精度却低于其他对比算法。由此可知,SAOLA和α-investing所选特征子集中存在较多冗余特征。
观察表2-表5发现,OFS-JNB算法所选特征个数与Fast-OSFS和OFS-Density保持在同一水平,在大多数数据集上均明显小于SAOLA和α-investing。
为了更加直观地对比6种算法在不同分类器上的分类性能,采用箱型图对实验结果进行分析,结果见图1、图2和图3。由图可得如下结论:
在总体水平上,OFS-JNB算法在8个数据集上的3个分类器上预测精度的中位数(平均性能)都排在第一。
OFS-JNB算法在KNN、LSVM分类器下,上四分位数和下四分位数的分布较为紧密,且集中分布在较高的分类性能区域。在CART分类器下,虽然上四分位数和下四分位数分布较为松散,但都集中分布在较高的分类性能区域。
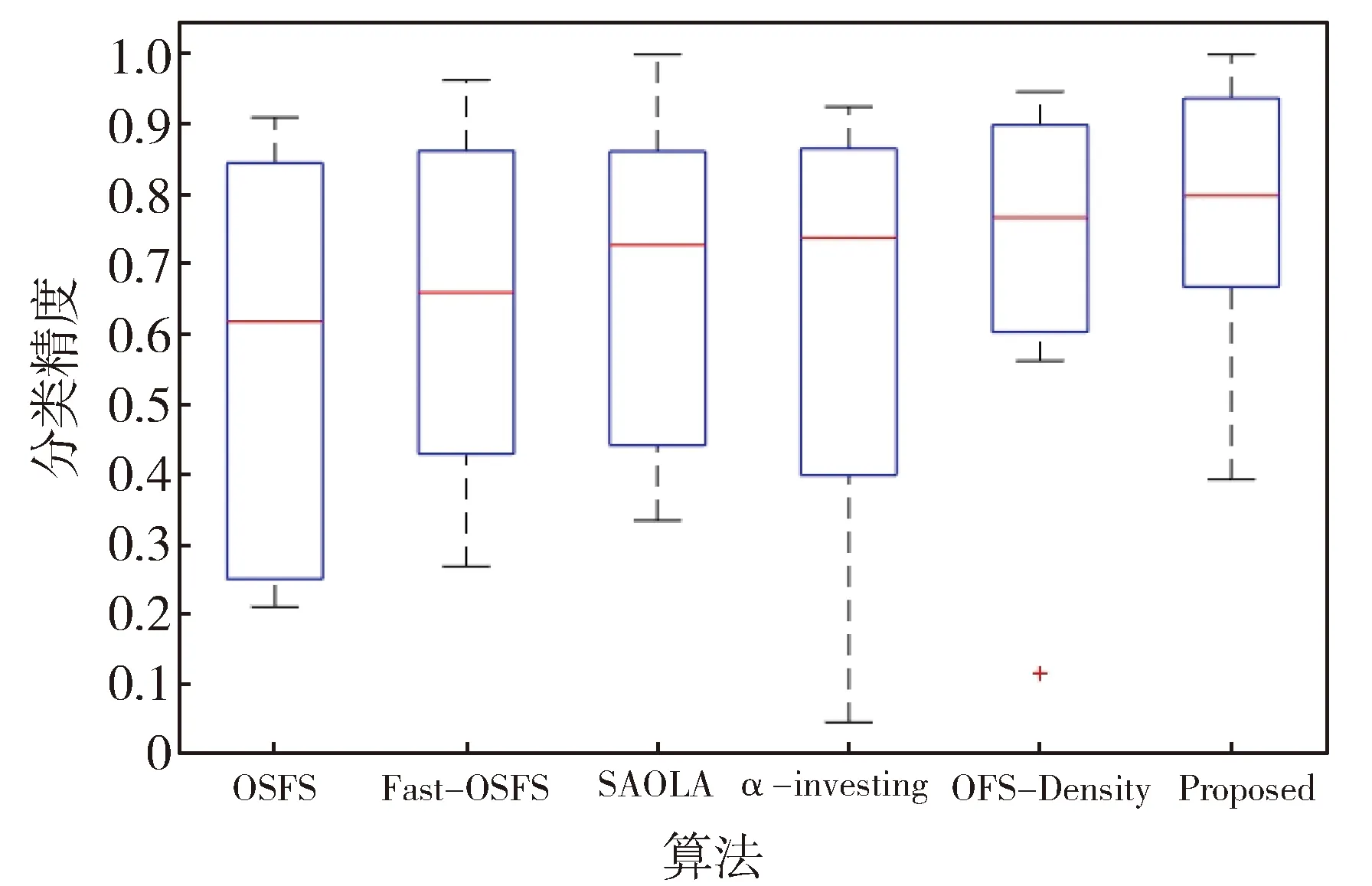
图1 各算法在KNN分类器上的盒形图对比Fig.1 Box plot comparison of algorithmswith KNN classifier
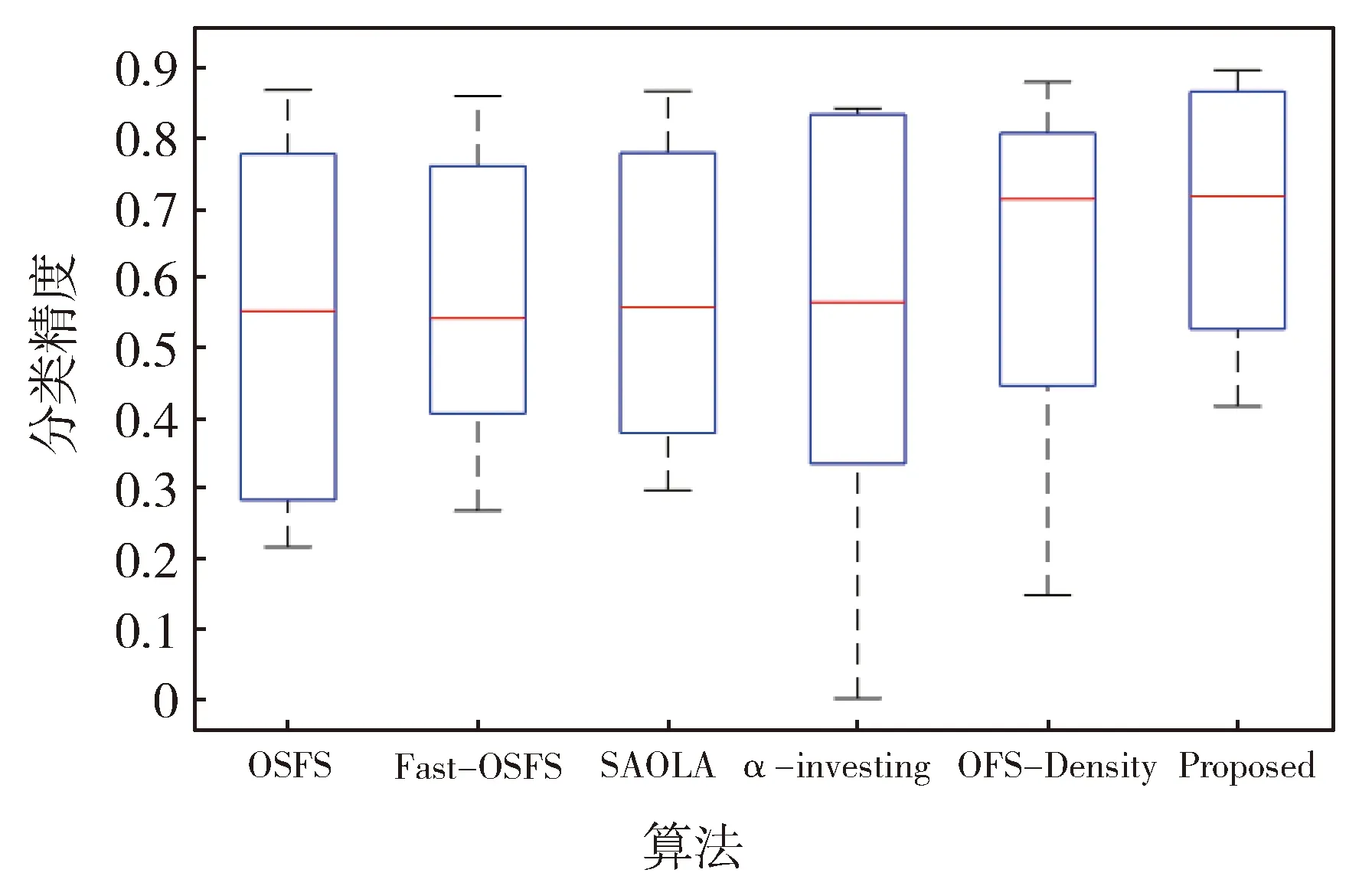
图2 各算法在CART分类器上的盒形图对比Fig.2 Box plot comparison of algorithmswith CART classifier
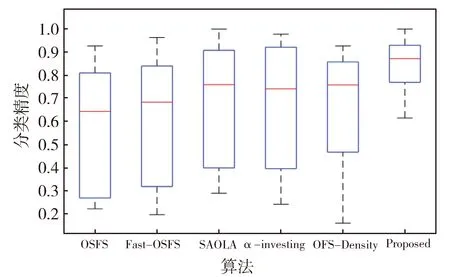
图3 各算法在LSVM分类器上的盒形图对比Fig.3 Box plot comparison of algorithmswith LSVM classifier
由此可得OFS-JNB算法预测精度优于其他算法且更稳定。
4 结论
在线流特征选择作为一种以在线方式处理流特征的新方法,近年来备受关注,并在处理高维数据问题方面发挥了关键作用。然而,传统基于邻域粗糙集的在线流特征选择方法在计算属性依赖度时,仅利用下近似来计算决策属性对于条件属性集合的依赖度,而忽视了边界区域中存在的有用信息。基于上述情况,本文提出联合邻域边界的在线流特征选择算法(OFS-JNB)。定义了一种计算属性依赖度的新方法,使得边界域中的信息得以利用。同时,依据“在线依赖度分析,在线重要度分析和在线冗余度分析”三种评估准则,选出高依赖度、高重要度且低冗余的特征子集。在8个数据集上的实验结果表明,OFS-JNB算法在预测精度上要优于传统的在线流特征选择算法。今后,我们的工作将讨论如何将该方法扩展应用于多标签数据集上。
