基于电磁力滤波的潜载定向能随动系统振动控制

刘宗凯, 李占江

(1.南京理工大学 自动化学院， 江苏 南京 210094;2.南京越博动力系统股份有限公司， 江苏 南京 210094)

0 引言

搭载在潜航器上的光电桅杆是集图像处理、光学跟踪、高精度测量等关键技术为一体的潜载光电跟踪与瞄准装置，它主要应用于海面搜索、海空目标信息采集等领域，也是未来战争中潜载激光定向能武器得以应用的关键载体。潜载及光电桅杆的结构如图1所示，其主要是由潜航器艇体、指挥塔围壳、螺旋桨推进器、光电桅杆、光电跟踪与瞄准装置所构成。不同于传统的武器系统，定向能武器的光电跟瞄系统需要连续跟踪目标，并引导激光束持续而稳定的聚焦在目标区域，且保持至少20～30 s[1]，这就使得对其跟踪精度的要求要比传统武器高1～2个数量级，因此与其相配套的光电跟瞄系统需要具有极好的振动隔离能力和光轴稳定控制能力。

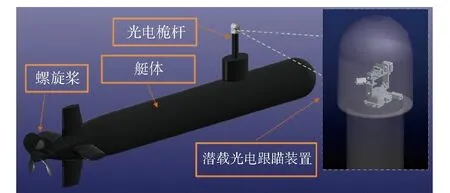
图1 潜航器与跟踪瞄准系统原理图Fig.1 Schematic diagram of submarine and tracking and sighting system

潜航器在水下高速潜行时，由于黏性边界层的剪切作用，当来流绕经艇体各附体时会诱发多种尺度的涡，高雷诺数条件下流体微团的轨迹极其紊乱，并随时间变化很快，这使得多尺度涡的生成和脱体显现出更多的随机性，黏性边界层的不确定演化将使大部分旋涡无法与绕物体的切平面保持对称，从而引起流体的横向运动，这些运动将会改变涡旋的形状和排列，一些小尺度的涡旋会在一定范围内随机波动(湍流脉动)。对于较高雷诺数的情况，则会导致边界层分离并诱导出形态各异的脱体涡，同时引起力和转矩的明显波动。对于更高雷诺数的情况，由于湍流的形成，使得绕过物体的涡，及其所受的力和转矩的波动更为复杂。这些波动导致了光电桅杆产生了更多的振动与噪声，制约了激光武器系统跟踪精度的提高。

为了增加跟踪的稳定性，滤除跟瞄过程中出现的扰动及噪声，工程应用中通常采用两种方法：第一种是信号处理法，通过数值滤波算法或者数字模拟电路来隔离高频信号，但是这种处理方法会增加数据转换时间，不利于系统时钟的同步；第二种是振动隔离法，对于潜航器在不考虑机械振动、螺旋桨形变的前提下，其振动主要源于湍流所引起的压力脉动[2]。此外，对于带螺旋桨推进的潜航器，在航行过程中潜航器尾迹也会是一种极不均匀的流场，其会对螺旋桨的稳定推进[3-4]以及潜载光电跟踪系统的瞄准精度产生不利影响。

为了提高潜航器的稳定性，消除不必要振动与噪声。科研人员研究了流致噪声随潜航器结构的变化，并在艇身和附体交界处使用了一个马蹄涡发生器，采用边界元法对潜航器周围的噪声进行了模型预测，同时研究了不同壳体厚度和纵向梁数对潜航器尾部螺旋桨噪声的影响[5-6]。Özden等[7]和Chase等[8]对美国国防部高级研究计划局(DARPA)螺旋桨推进的SUBOFF潜航器流场结构和噪声分布进行了数值分析。Wu等[9]研究了潜航器近壁区域马蹄涡的分布和演变。

电磁流体控制作为主动流动控制的一种方法，也被应用到振动控制上，对于海水这种弱电导率溶液(5～6 S/m)，通过电磁激活板表面施加的电场与其表面永磁体所激励磁场的相互作用便能激励出电磁力，进而改变其壁面边界层结构。这种电磁激活板可以排布在艇体表面形成用于调控边界层的电磁力，以起到减阻、增升、抑制流动分离的作用[10-12]。这种表面贴体的电磁激活板在调控边界层的同时并不增加任何的机械部件，也不需要改变受控体外形，可以仅通过调节输入电压与波形，方便地改变电磁力强度与时空分布。之前有科研人员数值研究了在有限长圆柱体表面施加对称或非对称的电磁力以实现对圆柱绕流流场的调节[13]，也有的采用了其他一些相关的数值方法和电磁流体控制方法来研究剪切来流下的涡传导振动[14]、微尺度流体运动[15]等。先前研究中鲜有探究在自由来流环境下流场扰动对跟瞄误差影响，更没有通过电磁力滤波抑制振动的方式来改善控制系统的抗扰动能力，本文通过边界层控制来抑制湍流脉动和潜航器振动为抑制潜载光电桅杆的输入噪声提供一种新颖的滤波方法。

1 研究流程

图2为本文所探讨问题的流程图。由图2可以看出本文主要分四部分内容：流场仿真、扰动解算以及粗通道/精通道快速反射镜补偿控制。

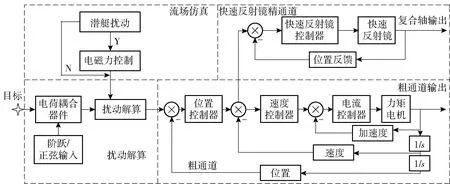
图2 电磁力滤波的仿真流程图Fig.2 Simulation flow chart of Lorentz force filter

1) 流场仿真。本文主要探索了雷诺数在1×107条件下，6°偏航角和10°俯仰角的潜航器在施加和未施加电磁力条件下，艇体周围湍流脉动、压力矩变化对潜载光电桅杆跟踪精度的影响。之所以选择6°偏航角和10°俯仰角是由于潜航器运动和转向过程主要是这两个角度产生变化的，两个角度的不同是为了突出不同的方位和俯仰角各自对控制效果的影响，同时选择的攻角值较小也是为了避免大攻角所引起的计算不易收敛的问题。

2) 扰动解算。本文中，为了获得艇体振动与最终控制效果之间的相互联系，需要将大地坐标系下湍流压力脉动对潜航器力矩的扰动转化为光轴坐标系下方位角和俯仰角的变化。

3) 粗通道、精通道/快速反射镜补偿控制。数值分析时，对复合轴跟瞄系统进行了建模，并在此基础上，获得了粗通道、精通道的稳态输出误差和误差轨迹的密度分布。通过边界层控制来抑制湍流脉动和潜航器振动，降低了光电桅杆的输入噪声，提升了定向能武器的作战效能。

2 磁流体动力学分析的基本模型和数值方法

2.1 基本模型

图3为仿真用的潜航器模型及尺寸图。该模型由半圆形的头部(半径为0.06l)、圆柱形的艇体(圆柱长为0.69l)、椭圆柱型指挥塔(圆柱高为0.06l、长轴半径为0.045l、短轴半径为0.02l)以及类圆锥形尾部(长为0.25l)，其中l为潜航器长度也是特征长度。如图3指挥塔周围均匀排布的条带是电磁激活板的电极和磁极，用于激励电磁力，调控指挥塔周围的流场。

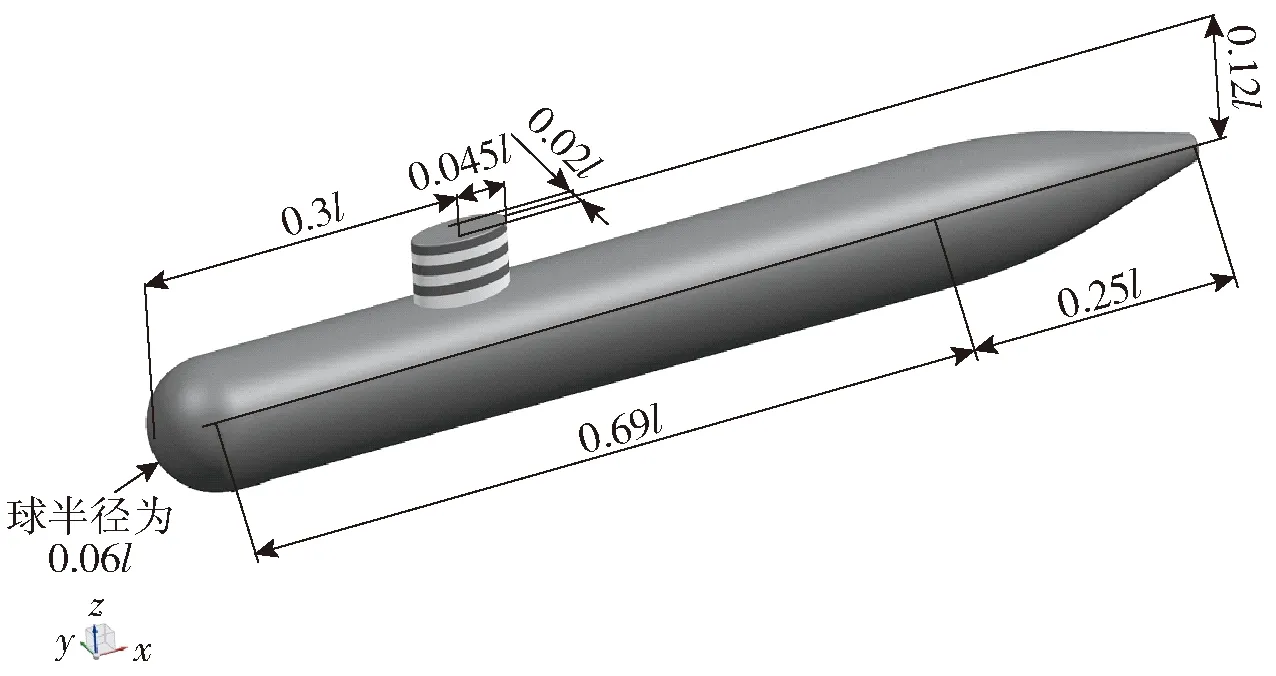
图3 潜航器模型及尺寸Fig.3 Submarine model and sizes

计算区域大小为4l×2l×2l，入口来流沿x轴正方向，潜航器前缘点在右手坐标系的原点处，其位于口面下游0.5l处。x轴指向下游，y轴指向右舷，z轴垂直向上(无攻角)。计算区域的入口和出口分别定义为速度入口边界条件和压力出口边界条件，其余4个侧面分别定义为压力边界条件，压力为常数，法向速度为0 m/s. 另外，将潜航器壁面均定义为无滑移边界条件。

2.2 控制方程、网格离散和求解方法

在本文采用的是带有电磁力源项的无量纲流体力学控制方程，如(1)式～(6)式所示：

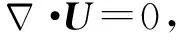
(1)

(2)

(3)

(4)

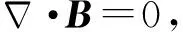
(5)

(6)

式中：U=(u,v,w)是速度矢量；t为无量纲时间；p为压力；Re为潜航器长度雷诺数；N为无量纲电磁力作用参数；F为无量纲电磁力；E为电磁场强度；B为磁通密度矢量；J为电流密度矢量；μ0、ρe、e0分别为磁渗透、电荷密度和海水电导率。 (2)式中无量纲电磁力F可以由磁通密度矢量B和电流密度矢量J来表示：

(7)

式中：j0和B0分别表示在近壁面区域的最大电流密度和磁传导密度[16-17]；J可以由Ohm定律得到，

J=σ(E+U×B)，

(8)

σ为电导率，对于弱电解质溶液，例如海水，其电导率σ非常小。相比于电磁场强度E，传导项U×B在(8)式中可以被忽略。因此在三维模型中，可以忽略感应项对电磁力的影响。因此，无量纲洛伦兹力F可表示为

(9)

在数值分析中，壁面的电磁力强度分布可以简化为仅随壁面距离增加不断衰减的指数型函数：

F=Ne-(π/a)de*，

(10)

式中：N代表了电磁力与流体惯性力的比，可以被写为

(11)

ρ为流体密度，U∞为来流入口速度；e-(π/α)d是电磁力衰减函数，a表示电磁力渗透深度的常量，这里取a=l/10；d表示壁面法向距离；e*为壁面单位切向矢量[18]。

在模拟中，流动控制方程(1)式和(2)式，采用Bell-Colella-Glaz的2阶迎风格式对对流项进行离散。扩散项采用Crank-Nicholson方法进行离散，其具有2阶精度和无条件稳定性。时间和空间项均以2阶精度离散。这里使用了直接数值模拟(DNS)法对整个流场进行求解，这种方法直接应用瞬时的Navier-Stokes方程对湍流进行计算，不依赖于任何流体模型。科研人员也对该DNS方法所得到相关问题的结果与实验进行了比较和验证[19]，本文数值方法的正确性在文献[20]中已经进行了验证。

3 绕流流场演化以及流体动力学特征

3.1 流场演化

图4和图5显示是在时间t为5 s，15 s和50 s 3个不同时刻处潜航器周围及其下游涡量场分布。其中图4为未加电磁力(N=0)的情况，图5为施加电磁力(N=1.5)的情况。对有无电磁力作用的对比研究最主要是通过流场的演化来更进一步分析电磁力滤波的真正作用机理，即它是如何延缓流动分离、减少阻力和升力波动，并最终抑制不同尺度涡的。

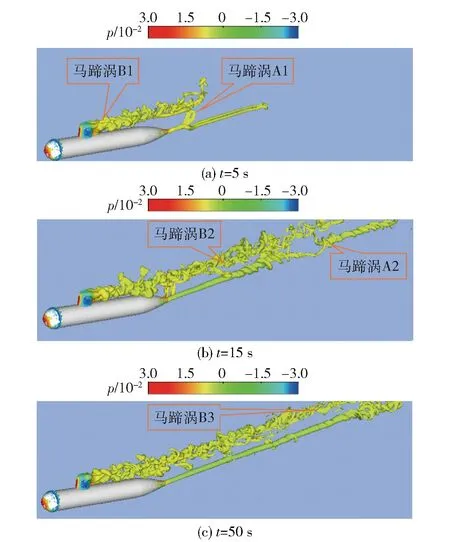
图4 潜航器涡量场的侧视图(N=0)Fig.4 Side views of submarine vortex field (N=0)

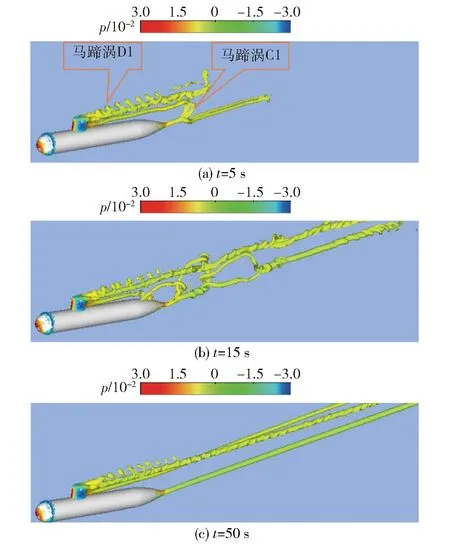
图5 潜航器涡量场的侧视图(N=1.5)Fig.5 Side views of submarine vortex field (N=1.5)

由图4可以看出，当来流绕过指挥塔上半部时，由于边界层的剪切作用和指挥塔壁面的阻碍使得近壁区域的流体损失了较多的动能，进而产生了速度梯度并引起了流体的旋转运动。在指挥塔上半部形成较为紊乱的马蹄涡序列B1，它是所属区域大尺度涡的拟序结构，其特征尺度与绕流障碍物尺度基本一致；在指挥塔下游出现了大尺度的耗散涡，这些涡绝大多数都产生于指挥塔边缘区域，在涡序列生成和脱体过程中，会造成转矩的持续波动。在t=5 s时刻(见图4(a))，入口最初来流绕过艇体后会在其下游形成一个显著地马蹄涡A1，其具有与艇体直径相同的尺度，A1涡在向下游移动过程中开始耗散并行成了一系列较小的不规则的涡，并一个接一个的消失(见图4(b))。随着时间的推移，流场逐渐趋于稳定。同样，马蹄涡B1也逐渐衰减成中等尺度涡B2和小尺度耗散涡B3. 为了方便研究，只讨论稳定时刻，即20 s以后的转矩曲线。

错综复杂的脱体涡主要产生于潜航器指挥塔的上半部分，为了消除其影响，需要抑制不稳定的耗散涡，本文在近壁边界层上施加流向电磁力，以减小边界层的剪切效应。图5为在N=1.5、电磁力作用下3种不同时刻时，潜航器等涡量面演化的对比图。由图5可以看出，当进口来流绕过潜航器及附体时，流场下游会形成相对规则且间隔一致的马蹄涡序列D1，并在艇体下游形成和未加力一样的马蹄涡C1. 相对于图4中未有电磁力控制的情况，指挥塔下游的大尺度扰动涡会逐渐被抑制，一些小尺度高频扰动涡被滤除。相应地，在这些频带范围内的湍流脉动、压力波动会被显著地抑制。这就是使用电磁力作为优化滤波器的机理所在。

3.2 流体动力学特征

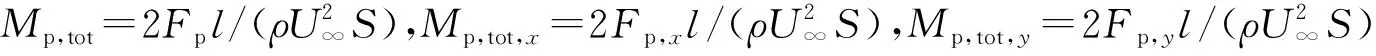
图6为压力矩系数随时间变化曲线。潜航器头部前缘点和力矩参考点都位于坐标原点。图6(a)没有施加电磁力控制时，由于6°偏航角和10°俯仰角的存在，使得潜航器的右弦成为迎风面，迎风面在来流冲击下使潜航器产生绕z轴负向旋转的趋势，因此Mp,tot,z是负值，波动范围为-0.000 8～-0.000 7. 指挥塔在入口来流冲击下，使得潜航器尾部形成了一个绕y轴向下转动的趋势，因此Mp,tot,y呈现为正且大约为0.000 45. 这种扰动同样也影响了潜航器的滚转力矩Mp,tot,x，其值大约是-0.000 25，较前两种情况略小。图6(b)是通过在指挥塔上半部施加流向电磁力后的压力系数曲线。由图6(b)可以看出，施加电磁力后由于边界层被抑制，压力脉动被消除，使得Mp,tot,z的波动比未施加电磁力时减小很多。对比图6(a)和由图6(b)可以看出，电磁力可以有效地抑制力矩波动，获得所期望的滤波效果。

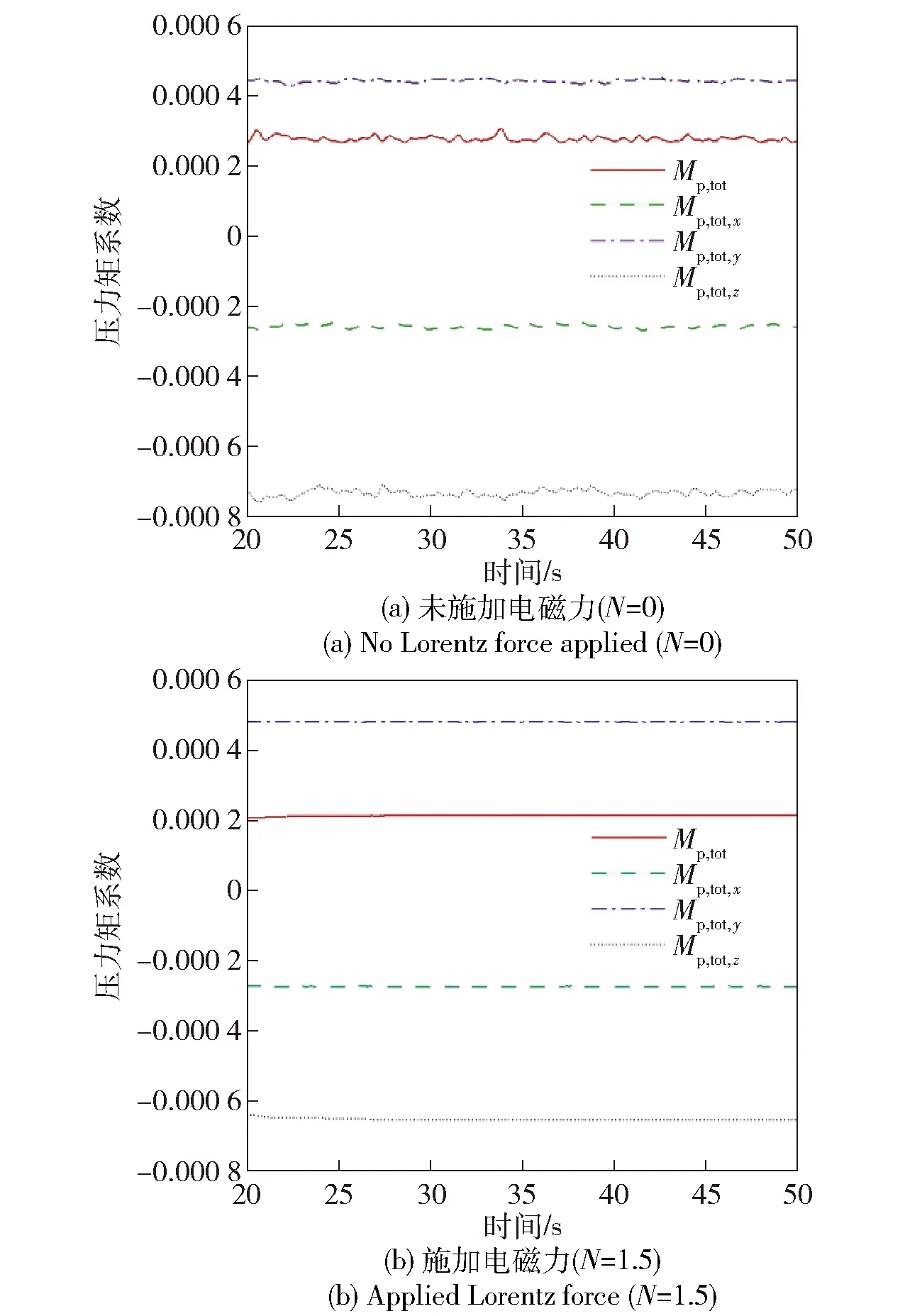
图6 压力矩系数的时间曲线Fig. 6 Time histories of pressure torque coefficients

这些力矩扰动(在大地坐标系下)最终会反应到光电桅杆方位角和俯仰角的波动上(在光轴坐标系下)。这里涉及一个力矩与角位移之间的变换，该变换系数主要取决于潜航器自身质量以及旋转中心的位置。在数值模拟中，可以将变换系数定义为

(12)

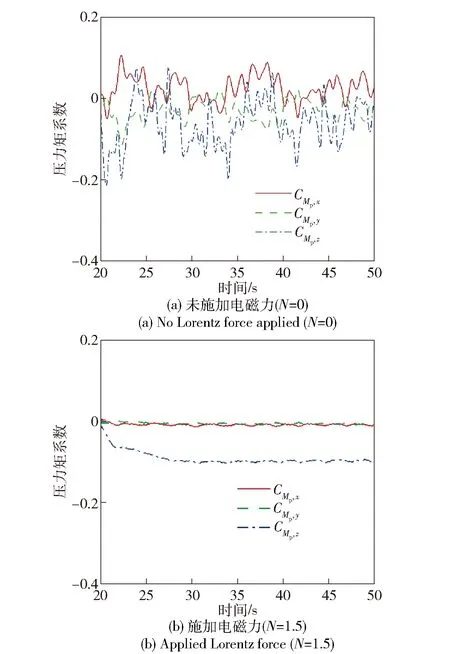
图7 压力矩系数绕20 s初始值处的波动Fig.7 Time histories of pressure torque coefficients around their values at 20 s

图8显示的是施加和未施加电磁力时x轴、y轴、z轴3个方向的力矩系数频谱图。图8(a)中CMp,x、CMp,y、CMp,z的最大幅值大都出现在0～0.4的低频范围内，其幅值分别约是0.018、0.020和0.025. 然而，随着频率的增加，噪声幅值也迅速衰减，当频率大于2 Hz时这3种情况的波动幅值都基本消失。这三者之中CMp,z的幅值最大，并出现在频率为0 Hz位置处，但由于电磁力的作用，如图8(b)在相同频率处CMp,x、CMp，y、CMp,z的幅度值较未加电磁力时削弱很多。

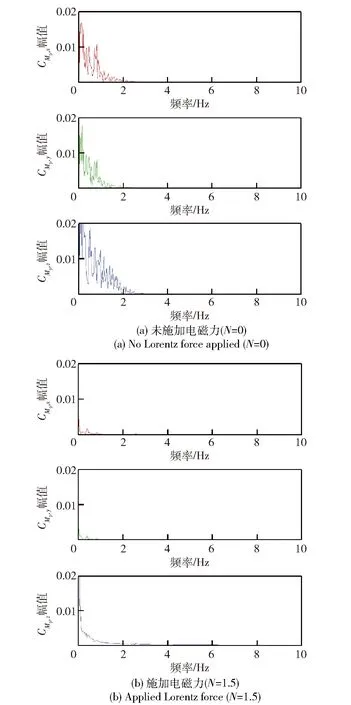
图8 压力矩系数的傅里叶变换Fig.8 Fourier transform of pressure torque coefficients

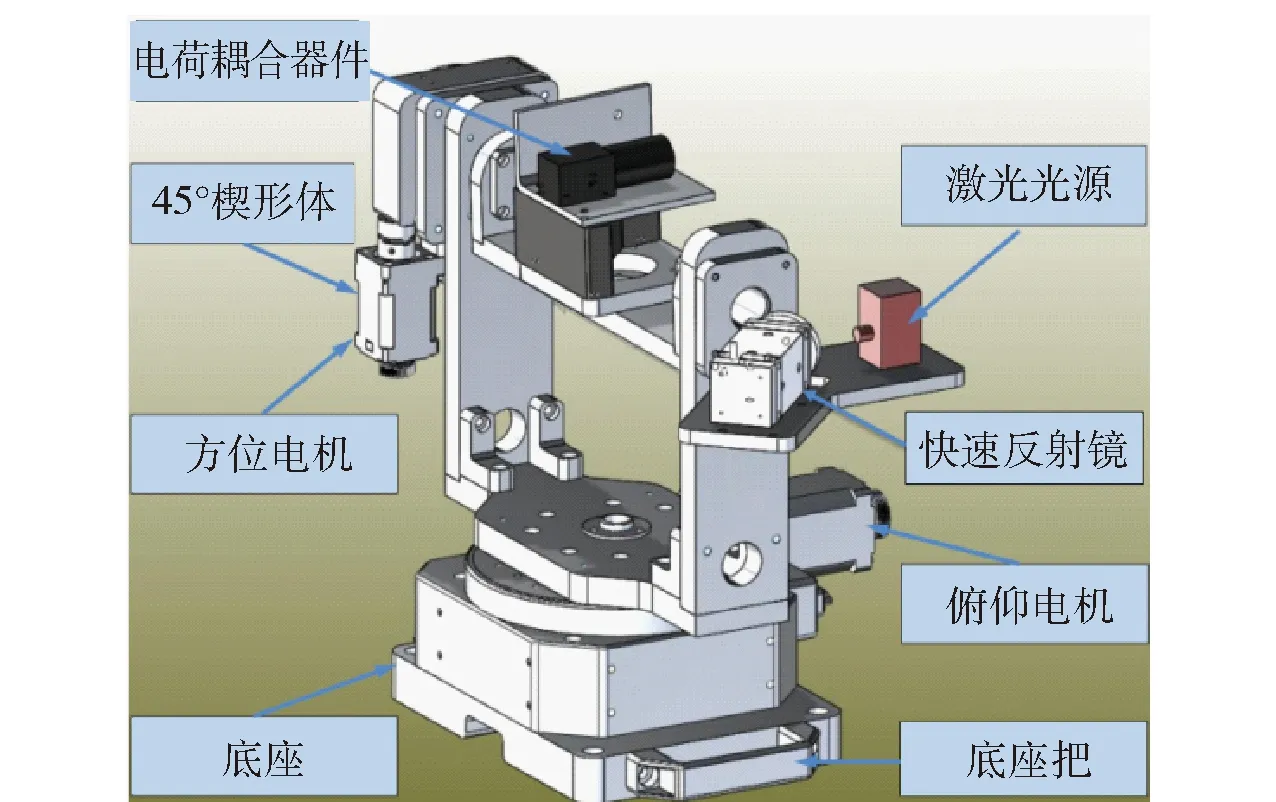
图9 复合轴光电跟瞄系统结构图Fig.9 Structure of tracking and sighting system

4 跟瞄系统建模与视轴扰动坐标变换

4.1 光电跟瞄系统的结构和建模

图9为潜载定向能随动系统复合轴光电跟踪的原理结构图，图10为复合轴光电跟瞄系统实验装置图。该复合轴跟踪系统主要是由两个力矩电机驱动的方位和俯仰转台、一个快速反射镜、一个电荷耦合器件以及一个搭载反射镜的45°楔形体所构成。在实验过程中，激光由一个位于左侧平台上的激光光源射出，首先经由快速反射镜反射后，沿俯仰平台轴线孔洞射入，经过45°反射镜反射后向前方射出。

图10 复合轴光电跟瞄系统实验装置Fig.10 Experimental facility of tracking and sighting system

4.2 精通道快速反射镜的原理与建模

精通道的光束控制采用的是由压电陶瓷堆叠驱动的快速反射镜，该反射镜由一个矩形的长方体和漏出头部的4个位于同一个平面上可以伸缩的柔性支点所构成，在驱动电压控制下该反射镜可以绕其两个相互垂直的中心轴实现方位和俯仰的偏摆，进而可以对其表面搭载的反射镜镜片姿态及反射光方向进行精确调控[21]。本文中快速反射镜的物理摆角为±12.5 mrad，闭环控制精度为5 μrad. 实验中通过频谱分析仪测量了快速反射镜在闭环状态下的频率响应曲线，在此基础上可以将其闭环传递函数[22-23]简化为

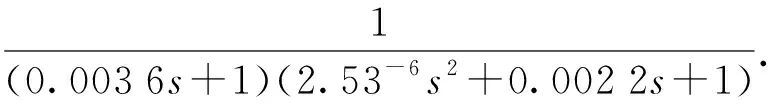
(13)

4.3 粗通道直流力矩电机的数学模型

由电枢电路的电压平衡方程可推导出直流转矩电机的传递函数。为了简化研究，忽略了电流波动和扰动转矩，可将直流转矩电机近似为线性元件。假设方位转矩电动机和俯仰转矩电动机的传递函数和转动惯量是相同的。角速度和控制电压的传递函数可以写成：

(14)

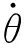
(15)

(16)

4.4 粗、精复合轴跟瞄系统的传递函数

图11是在控制回路中应用PID/PI控制器后系统的仿真流程图。由图11可以看出，力矩电机的速度环采用PI控制器以提高该环节的响应速度，位置环采用PID控制器(PID1)；快速反射镜也采用PID控制器(PID2)来实现控制。每个PID或PI控制器的参数都由“等幅振荡”法来确定。通过MATLAB Simulink仿真得到方位角和俯仰角的最终跟踪误差。该系统的输入信号为潜航器视轴坐标系下方位和俯仰扰动，这个扰动需要力矩系数经过坐标变换来得到。

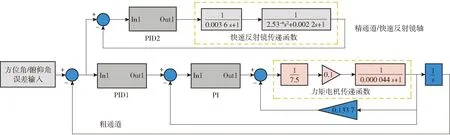
图11 复合轴控制下的MATLAB仿真模拟图Fig.11 MATLAB simulation diagram of composite axis system

4.5 艇体与光轴扰动之间的坐标系变换

假定电荷耦合器件采样周期Δt约为0.01～0.02 s，潜航器的扰动并没有使得目标超出视场范围，也就是说目标信息自始至终可以获取。光电桅杆与艇身固连在一起，因此桅杆会与艇体保持一致运动，艇体的力矩波动将会随艏摇/偏航角αH、横摇/滚转角αP和纵摇/俯仰角αR的变换直接反应到光电桅杆上。当潜航器仅依次发生艏摇、横摇以及纵摇时大地坐标系下的目标点G(x,y,z)在甲板坐标系下分别变为GH(XH,YH,ZH)，GR(XR,YR,ZR)和GP(XP,YP,ZP). 其表达式为

(17)

在大地坐标系下每一时刻目标G(x，y，z)的方位角和俯仰角可以由αH、αP、αR和Δt获得。由于间隔时间Δt较短所以每一步平移运动所引起的方位角和俯仰角变化量都很小。因此，本文仅仅考虑了力矩扰动所产生的旋转运动。接下来需要将舰艇坐标系下目标的信息转换为方位角Ad和俯仰角Ed，假设初始时刻的方位角和俯仰角分别为A0和E0，则可以写为如(18)式形式：

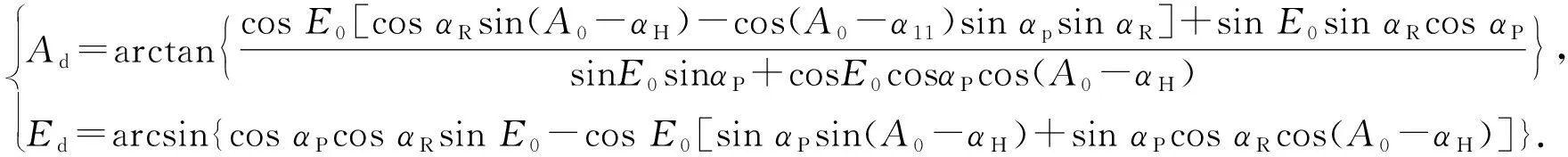
(18)

仿真时需要将力矩系数CMp，x、CMp，y、CMp，z的波动认为是(17)式、(18)式中αH、αP、αR的波动，并转化为目标在光轴坐标系下的方位角Ad和俯仰角Ed.

5 电磁力滤波对光斑能量密度分布的影响

图12显示了未加电磁力时仅经粗通道补偿后的方位角和俯仰角误差轨迹及其密度分布，其中ErrAd,DTM、ErrEd,DTM分别表示粗通道的方位角、俯仰角输出误差。通过对比，从中可以看出电磁力滤波的作用效果以及经粗通道、精通道补偿后的效果。系统输出误差轨迹密度分布在一定程度上也反映了光斑在目标位置区域的能量累积情况。ErrAd,DTM轨迹主要在-10×10-4～10×10-4之间波动，ErrEd,DTM则主要在-8×10-4～10×10-4之间波动。由图12中可以看出，在密度分布覆盖的区域出现了两个密度较大的峰值，它们的中心点分别位于(-1×10-4，1.8×10-4)和(2×10-4，-0.5×10-4)位置处。由图12(b)的三维密度分布可以看出，位于(2×10-4，-0.5×10-4)中心位置处的密度峰值较另一个中心位置处的值略大。

对于未有电磁力作用的情况，粗、精复合轴跟踪时其方位角/俯仰角误差轨迹的密度分布如图13所示，其中ErrAd,FSM、ErrEd,FSM分别表示精通道的方位角、俯仰角输出误差。粗糙的角跟踪误差进一步由快速反射镜进行补偿。因此，经过二次补偿后误差轨迹分布范围大幅度缩小，方位角和俯仰角误差范围约为：ErrAd,FSM为-3.5×10-5～4×10-5和ErrEd,FSM为-4×10-5～5×10-5，并仅出现一个单一的密度峰值，且其三维密度呈现出一个显著地高斯分布特征(见图13)。

图12 粗跟踪补偿后方位角和俯仰角误差 轨迹密度分布(N=0)Fig.12 Azimuth and pitch angle error density distributions after the coarse tracking (N=0)

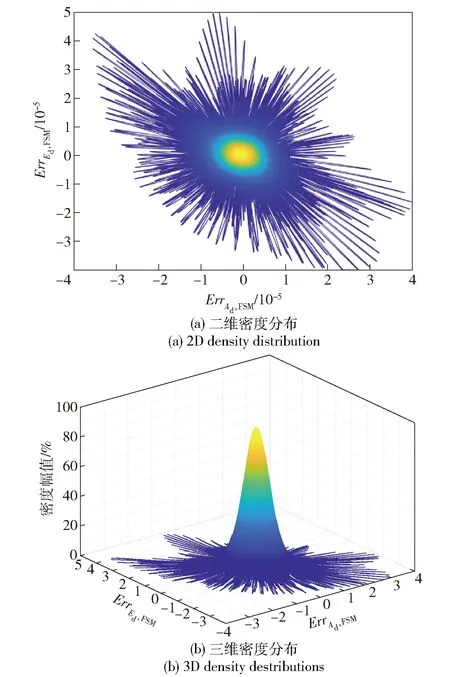
图13 精跟踪补偿后方位角和俯仰角误差 轨迹密度分布(N=0)Fig.13 Azimuth and pitch angle error density distributions after the fine/FSM tracking (N=0)

图14和图15显示了在N=1.5的电磁力滤波控制下粗通道和精通道复合补偿后的方位角和俯仰角误差轨迹及密度分布。如图14所示，在电磁力作用下粗通道误差的波动幅值显著地减小了。对于粗通道方位角的误差ErrAd,DTM波动范围为-8×10-5～4×10-5，俯仰角的误差ErrEd,DTM波动范围为-5.5×10-5～4×10-5. 图14所示，三维密度分布出现了两个相似的峰值。

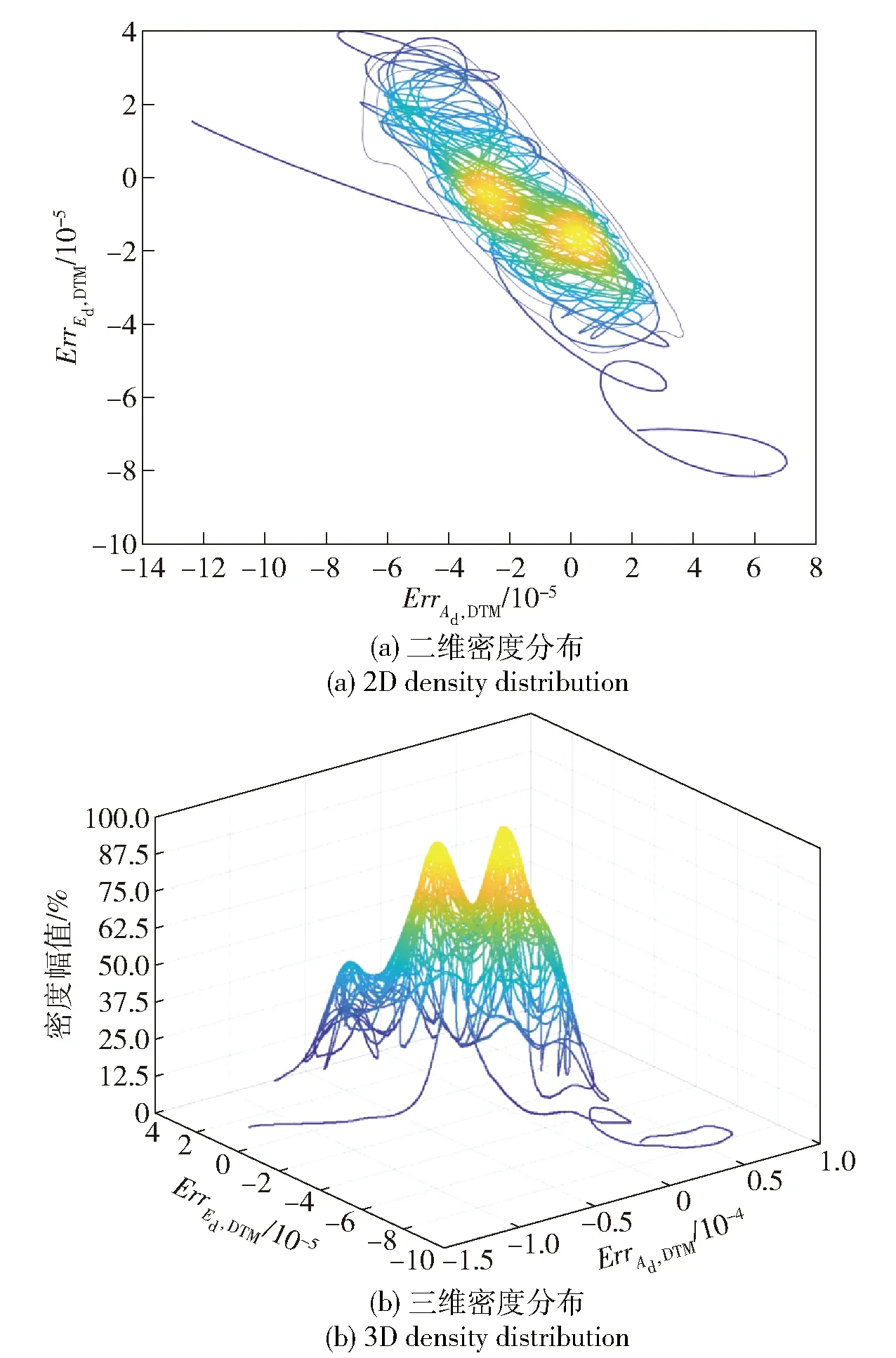
图14 粗跟踪补偿后方位和俯仰角误差 轨迹密度分布(N=1.5)Fig.14 Azimuth and pitch angle error density distributions after coarse tracking (N=1.5)

图15为在N=1.5的电磁力控制下精通道误差输出曲线的密度分布。由图15可以看出，跟踪误差ErrAd,FSM的主要分布范围为-3.5×10-6～3×10-6，ErrEd,FSM为-2.0×10-6～1.5×10-6. 同时，密度最大区域的直径范围已经从大约0.8×10-5缩减到1.0×10-6. 因此，在相同的控制参数下，经过电磁力滤波后其能量密度更加聚集。

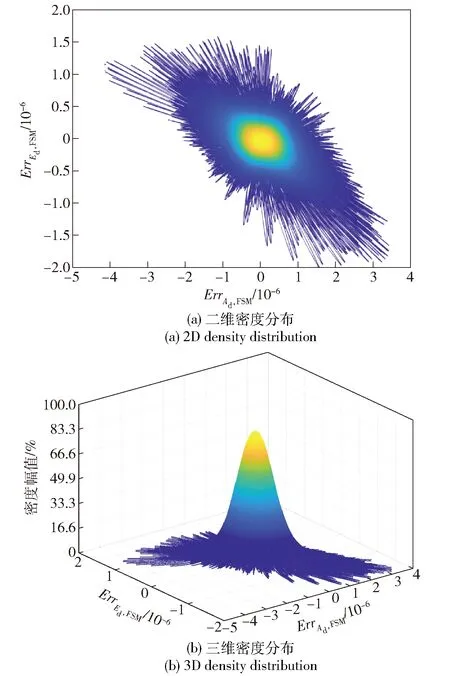
图15 精跟踪补偿后方位和俯仰角误差 轨迹密度分布(N=1.5)Fig.15 Azimuth and pitch angle error density distributions after fine/FSM tracking (N=1.5)

6 结论

本文通过电磁力抑制潜航器及其跟瞄系统的流体扰动以提高潜载定向能武器的跟踪精度。基于带指挥台的类SUBOFF模型体数值研究了在Re=107条件下，潜航器在水下潜航时其周围的涡量场演化和受力特征；经由坐标变换将流场扰动转换到光轴坐标系下，并基于所获得的复合轴跟瞄系统的传递函数数值仿真分析了有无电磁力滤波对跟瞄误差的影响。得到主要结论如下：

1) 潜航器下游绝大多数涡都源于潜航器指挥塔的边缘，这些涡主要是由该区域绕流物体边缘陡变后引起的流体及边界层扰动所诱发。因此在该区域(指挥塔的上半部分)壁面施加电磁力是抑制涡生成、消除湍流与振动的主要手段。

2) 由施加电磁力滤波前后的流场演化和频谱分析可以看出，电磁力滤波后指挥塔下游的大尺度脱体涡会逐渐减少，一些小尺度高频扰动涡被滤除。相应地，在这些频带范围内的湍流脉动以及力矩波动被显著地抑制。

3) 对于最终输出的精通道误差轨迹密度分布而言，电磁力作用前后其方位角误差ErrAd,FSM和俯仰角误差ErrEd,FSM范围分别由从未加电磁力时的-3.5×10-5～4×10-5和-4×10-5～5×10-5减少到施加电磁力后的-3.5×10-6～3×10-6和-2.0×10-6～1.5×10-6. 由此可见，局部电磁力优化滤波能非常有效地提高定向能武器光斑能量的密度。