GSO卫星系统布设中的通信干扰评估方法

董苏惠，姚秀娟，高翔，韩朝晖，闫毅，孙云龙

（1.中国科学院 国家空间科学中心，北京100190； 2.中国科学院大学，北京100049；3.中国人民解放军31007部队，北京100079）

据忧思科学家联盟（Union of Concerned Scientists）的统计数据，截至2019年9月30日，全球各类人造地球卫星共计2 218颗，其中低轨卫星1468颗，静止轨道卫星562颗，而中国拥有静止和非静止轨道卫星总数为323颗，成为继美国之后的第二大拥有在轨卫星数量的国家。在360°的地球静止轨道（Geostationary Satellite Orbit，GSO）上，平均不到1°就有一颗卫星。例如，划分给卫星固定业务（Fixed-Satellite Service，FSS）的Ku频段异常拥挤，受限使用已成为全球普遍的现象。频率和轨道资源日趋紧张，尤其是GSO卫星的资源竞争异常激烈，为卫星系统间的干扰分析提出了更加严峻的挑战。干扰分析方法及评估指标是多个系统间干扰分析的依据，如干扰噪声比（Interference-to-Noise Ratio，INR）［1］、载波干扰比（Carrier-to-Interference Ratio，CIR）［2-3］、载波与干扰和噪 声 比（Carrier-to-Interference and Noise Ratio，CINR）、等效噪声温度增量百分比（Percentage Increase in Equivalent Noise Temperature， PIENT）［4-6］等分析方法，国内外在该方面开展了大量的研究工作。例如文献［7］主要针对GSO卫星所使用的不同天线方向图对地面无线电中继系统造成的干扰进行了研究。文献［8］对降雨衰减统计数据与在同一频带内工作的相邻卫星造成干扰的地空链路进行了研究。文献［9］通过误码率性能分析了非对地静止轨道对GSO的干扰效应，主要分析卫星之间的角度对干扰的影响。文献［10-14］利用上述干扰分析方法对特定链路场景下2颗临近轨位卫星实例进行了仿真研究和干扰分析，提高了空间轨位资源利用率。上述文献所使用的分析方法对于理论计算具有一定的参考意义。本文利用国际电联（International Telecommunication Union，ITU）公布的国际频率信息通函（International Frequency Information Circular，IFIC）数据库，主要针对GSO卫星系统间同向链路的同频干扰进行定量化分析研究，提出了一种可以针对全球不同布设场景来进行干扰评估和计算的数学模型，该模型综合考虑了降雨、云雾、气体吸收引起的衰减以及馈线和极化损耗等影响因素，在保证卫星系统的可用度达到99.9%的情况下，明确了其最坏取值及干扰评估的条件和变化趋势，并在多条链路的集总干扰场景中充分考虑了波束间业务需求的不均匀性，可以作为GSO卫星系统间干扰评估和干扰规避的借鉴。

1 下行链路同频干扰分析方法

1.1 下行链路同频干扰场景构建

本节旨在从定量化分析的角度来研究GSO卫星系统地球站的分布对同向下行链路干扰分析结果的影响，在分析时构建的下行链路同频干扰场景如图1所示。图中：p′s0为干扰卫星信号发射到受扰系统接收端的最大功率密度；g′1（θ1）为干扰卫星天线在受扰地球站方向上的发射增益，θ1为干扰卫星发射天线的离轴角；g2（θ2）为受扰地球站天线在干扰卫星方向上的接收增益，θ2为受扰地球站接收天线的离轴角；lsi→e为干扰下行链路的传输损耗。

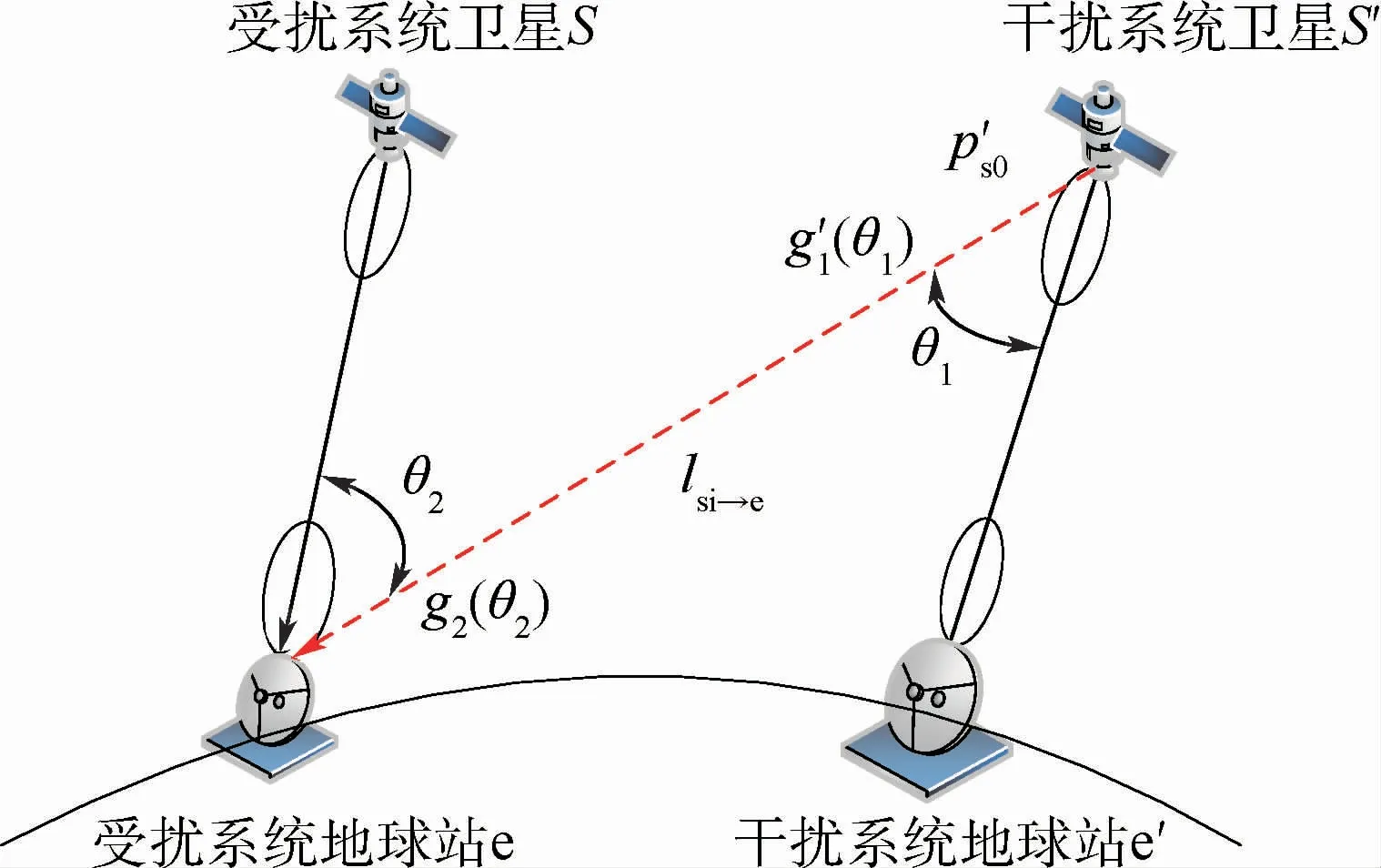
图1 同向下行链路干扰场景Fig.1 Co-directional downlink interference scenario

1.2 下行链路最坏干扰分析

受扰及干扰GSO卫星系统干扰场景所使用的波束及空口参数如表1所示，其中地球站天线方向图主要参考ITU公布的建议书ITU-R S.580-6［15］或者ITU-R S.465-6［16］，GSO星 上 天 线 方 向图参考建议书ITU-R S.672-4［17］。

在下行链路干扰分析场景中，本文主要考虑地球站在不同区域的分布对下行链路干扰噪声比I/N（I为受扰系统接收到的干扰信号功率，W；N为受扰系统接收机的等效噪声功率，W）的影响。在卫星系统干扰场景的波束及空口参数确定的条件下，天线离轴角和卫星-地球站的链路损耗是影响干扰分析的最重要因素，所以本文在初步选取干扰场景中所涉及的2颗GSO卫星的位置时，把卫星-地球站链路损耗这一重要参数作为选取依据。

图2为参考建议书ITU-R P.1511-2提供的全球地形海拔高度图［18］，在通信频率为25 GHz，地球站仰角为90°的条件下，采用表1参数计算得到的赤道上空GSO卫星-地球站链路损耗在180°W ～180°E上的分布情况，其中经度为正值代表东经，负值代表西经，因在该场景下的自由空间损耗为常量，分析时主要考虑降雨、云雾、气体吸收引起的衰减。

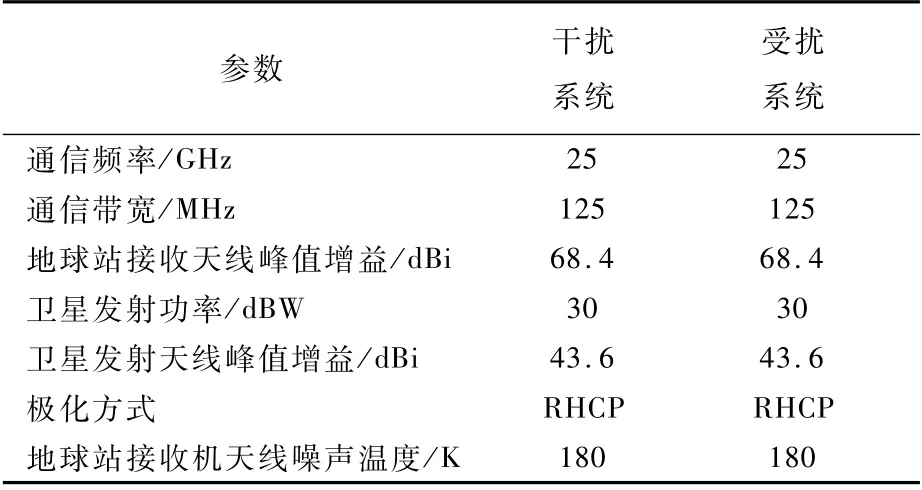
表1 GSO卫星系统下行链路干扰场景波束及空口参数Table 1 Beam and air inter face parameters of GSOsatellite system downlink interference scenario

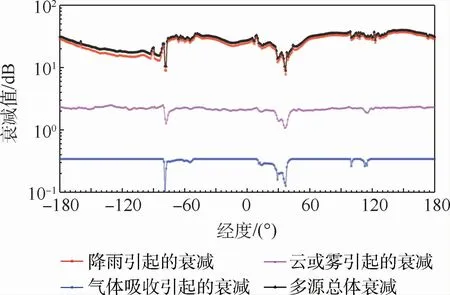
图2 在赤道180°W ～180°E上降雨、云雾、气体吸收引起的衰减分布Fig.2 Distribution of attenuation caused by rainfall，cloud，fog and atmospheric absorption at 180°W-180°E in the equator

由图2可知，在37°E位置附近由于降雨、云雾、大气等引起的多源总体损耗最小，最小值为8.90 dB，在该位置附近布设的GSO卫星的波束覆盖范围内，电波传播模型对干扰分析结果的影响较为明显，该位置可作为GSO卫星布设中干扰分析的初选值。

1.3 干扰系统地球站分布对下行I/N计算的影响

对干扰系统地球站在不同区域分布情况下2颗GSO卫星之间下行链路的I/N进行分析时，由于受扰地球站和干扰GSO卫星的位置是固定不变的，因此不论干扰系统的地球站如何分布，干扰下行链路的传输损耗lsi→e都是一个固定值，如图1所示。保持受扰系统卫星（0°N，37°E）及其地球站（10.0°N，37°E）和干扰卫星（0°N，34°E）的位置固定不变，在下行链路干扰分析中，采用建议书ITU-R P.1511-2提供的全球地形海拔高度图中的数值作为高度参考值［18］，建立干扰系统地球站地理信息分布族，该分布族是一组独立同分布的随机变量的集合，记作W：=｛W1，W2，…，Wn｝，Wi=［xwi，ywi，zwi］T，i=1，2，…，n，xwi、ywi、zwi为在地球固连坐标系下对应于x、y、z轴的位置坐标值。下行链路的数学模型函数（I/N）d=f（w）具体为［19-20］

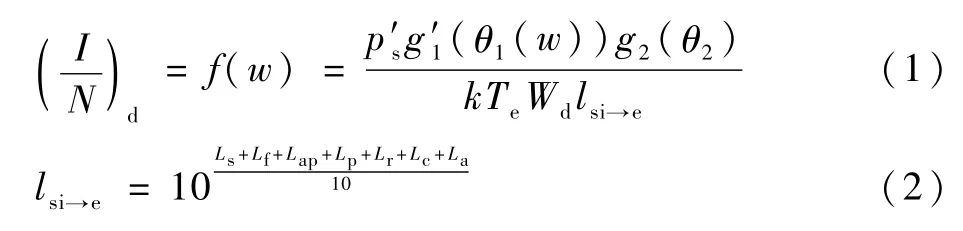
式中：p′s为干扰卫星在（干扰链路）重叠频带内的发射功率，W；Te为受扰地球站下行接收端的等效噪声温度，K；Wd为受扰系统下行链路的带宽，Hz；k=1.38×10-23J/K为玻尔兹曼常数；Ls为自由空间损耗；Lf为馈线损耗；Lap为天线指向误差损耗；Lp为极化损耗；Lr为降雨引起的衰减；Lc为云或雾引起的衰减；La为大气吸收引起的衰减［18，21-28］。

又因为f（w）与ln f（w）在同一w处取得极值，所以f（w）的极大值点也可从式（5）求得。

图3 干扰系统地球站在不同区域分布情况下的下行链路I/N变化曲面图和等值线图（未包括电波传播损耗）Fig.3 Downlink I/N variation surface map and contour map of interference system earth station in different regions（excluding electromagnetic wave propagation loss）

由图3（a）可知，当干扰系统地球站和受扰地球站间的纬度和经度差值都为0°时，即干扰系统地球站与受扰地球站在同一位置时，下行链路干扰最大，I/N最大值为-2.850 dB；在南半球高纬度地区下行链路干扰最小，I/N最小值为-35.614 dB。

如图3（b）所示，根据I/N的值，把干扰系统地球站的分布划分为A～F区，当干扰系统地球站在D、E、F区布设时，I/N值变化相对缓慢，在C区布设时I/N值变化较快，在B区布设时I/N值不变，为-22.849 6 dB，在A区布设时，I/N值出现陡升现象，该场景下I/N值与干扰卫星发射天线的离轴角θ1是二次函数的关系，即

1.4 受扰地球站分布对下行I／N计算的影响

保持受扰系统GSO卫星（0°N，37°E）和干扰卫星（0°N，34°E）的位置固定不变，同样地，采用全球地形海拔高度图给定的数值作为高度参考值［12］，建立受扰地球站信息分布族，该分布族也是一组独立同分布的随机变量的集合，记作V：=｛V1，V2，…，Vn｝，Vi=［xvi，yvi，zvi］T，i=1，2，…，n，xvi、yvi、zvi为在地球固连坐标系下对应于x、y、z轴的位置坐标。利用1.3节的结论，保持干扰和受扰系统的地球站在同一位置，对地球站在不同区域的分布情况进行进一步的干扰分析。对受扰地球站的分布而言，需要考虑的因素包括地球站仰角、海拔高度、当地降雨等情况。图4为在不涉及电磁波传播模型前提下，干扰地球站与受扰地球站重叠时2颗GSO卫星之间下行链路干扰噪声比I/N的分布曲面图，坐标轴分别代表地球站和受扰系统GSO卫星星下点间的纬度和经度间隔。

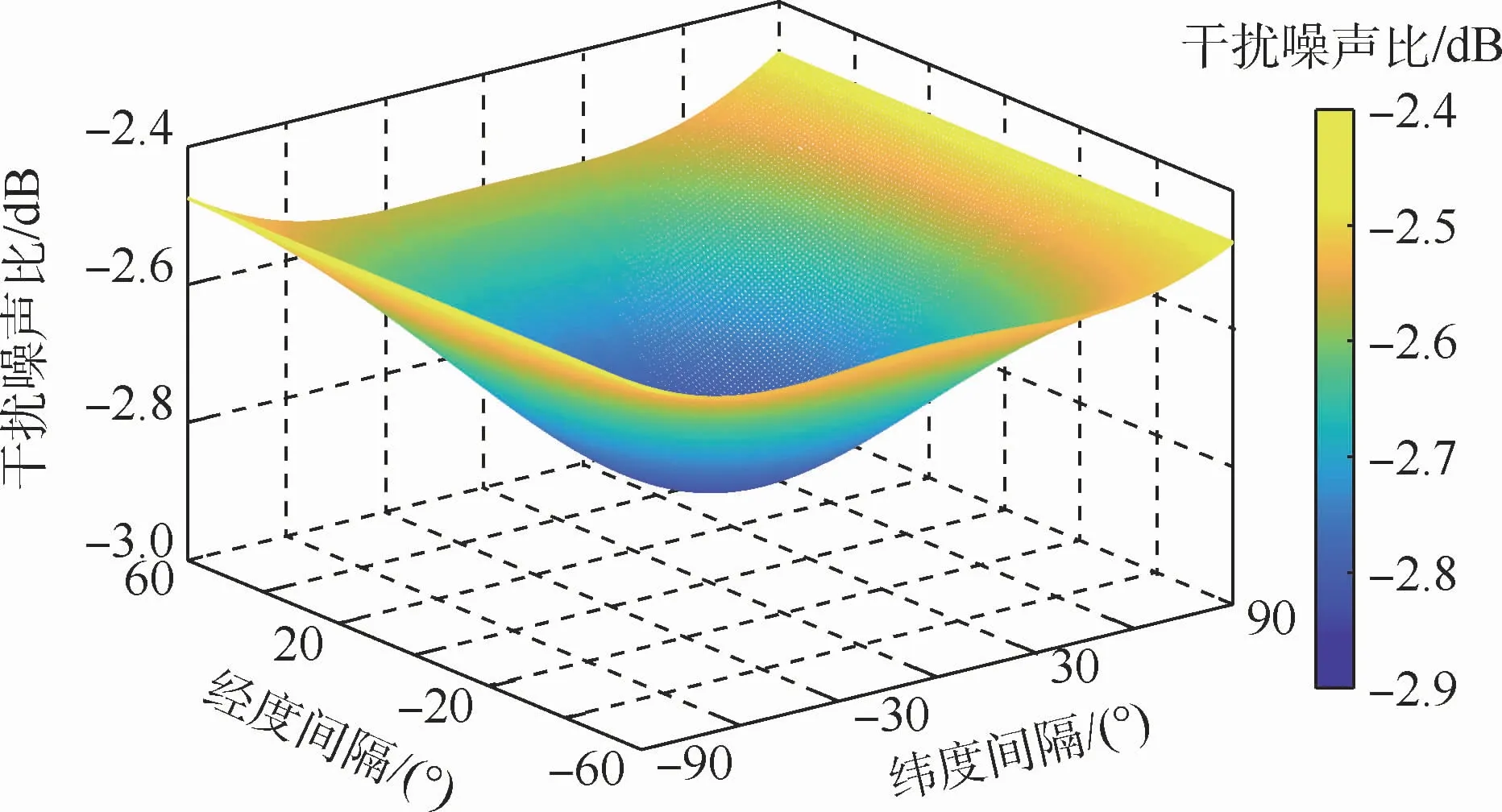
图4 地球站在不同区域分布情况下2颗GSO卫星之间的下行链路I/N曲面图（未包括电波传播损耗）Fig.4 Downlink I/N distribution surface map between two GSO satellites when earth stations are distributed in different regions（excluding electromagnetic wave propagation loss）

由图4可知，在不涉及电磁波传播模型前提条件下，保持受扰地球站与干扰系统地球站在同一位置，地球站在不同区域的分布情况下对2颗GSO卫星之间的干扰情况影响不大，I/N最大值和最小值之间只相差0.3823 dB，虽然地球站在干扰GSO卫星星下点位置时干扰链路的空间损耗最小，但是在该情景下考虑到受扰地球站接收天线的增益g2是离轴角θ2的函数，对干扰链路计算结果的影响程度要略大于空间损耗产生的影响。事实上，实际场景远比这复杂得多，因此，在选择受扰地球站最坏干扰情况时，还需要在干扰链路中考虑无线电波传播模型（雨衰、云雾和大气气体吸收）、指向损耗、极化损耗、馈线损耗和地球站仰角等情况。图5为地球站在不同区域分布时与干扰GSO卫星间仰角的情况。

由图5可知，当地球站在干扰GSO卫星的星下点位置时，地球站与干扰GSO卫星间的仰角为90°，在实际干扰下行链路分析时，还需考虑GSO卫星地球站的最小仰角，在一般工作条件下，根据ITU-R S.1503-3建议书提供的参考地球站最小仰角［29］为

根据式（9），可以初步排除仰角不符合条件的地球站分布，这样可以简化接下来要分析的模型。

图6（a）为在考虑电磁波传播模型前提下，干扰系统地球站与受扰地球站在同一位置时，地球站在不同区域分布情况下2颗GSO卫星之间下行链路的I/N分布曲面图，图6（b）为图6（a）对应的等值线图，它反映了地球站在不同经纬度对I/N数值和变化率的影响，坐标轴分别代表地球站和受扰GSO卫星星下点间的纬度和经度间隔。

如图6（b）所示，当地球站在A和B区域布设时，干扰最大，其中最大值出现在与受扰系统卫星星下点纬度差值为23°，经度差值为-11°的位置，即当地球站位置为（23°N，26°E）时，I/N最大值为-3.4374 dB。此外在B区域的（35°N，79°E）位置，I/N值也较大，为-3.528 5 dB。

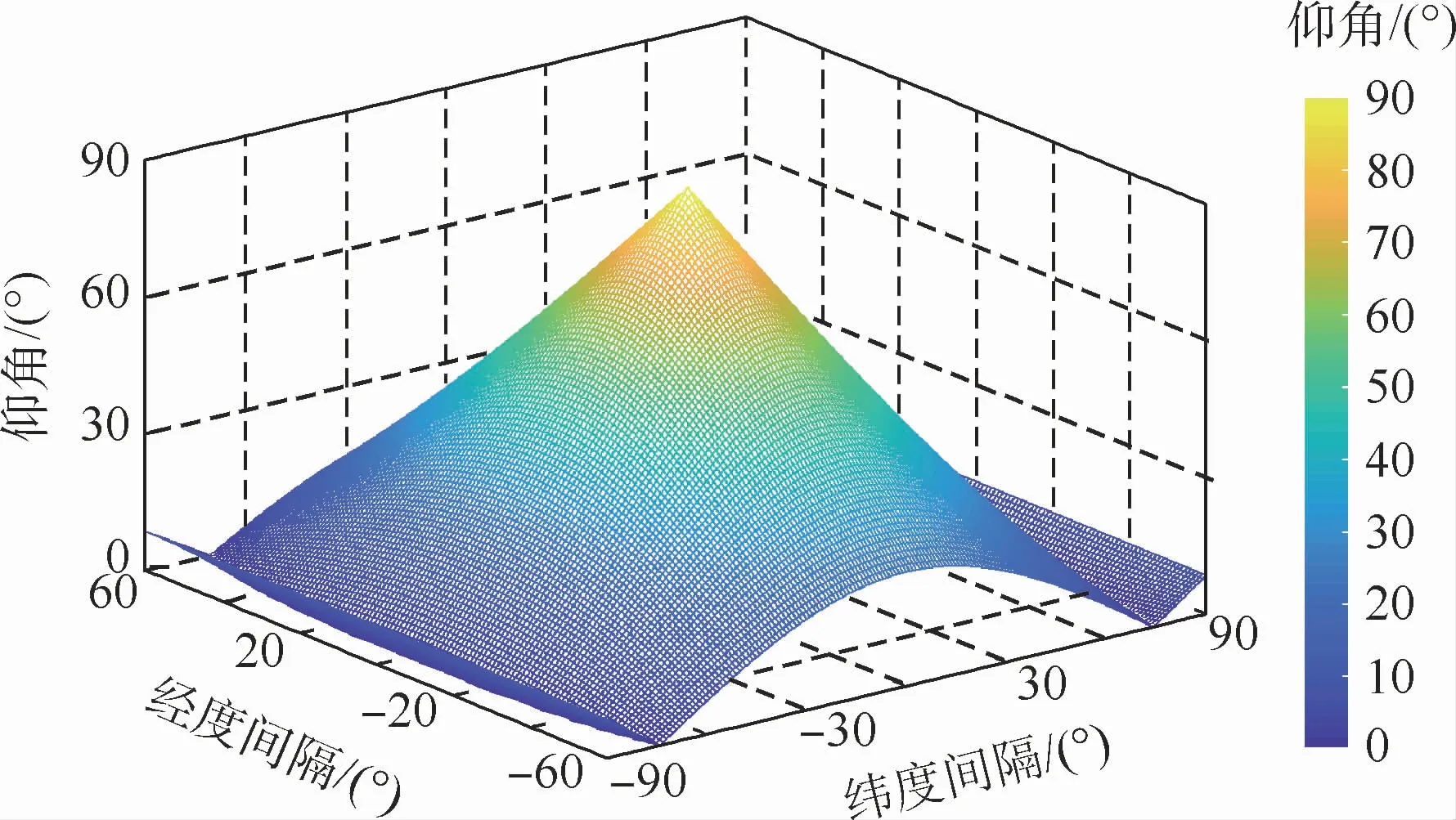
图5 地球站在不同区域分布时与干扰GSO卫星间的仰角情况Fig.5 Elevation angle between earth stations and interfering GSO satellite when earth stations are distributed in different regions

因为下行链路干扰分析结果不仅取决于地球站当地的环境，还取决于天线离轴角。为了权衡天线离轴角和卫星系统间链路损耗的综合影响，可基于上述计算结果，在（23°N，26°E）位置布设干扰和受扰地球站，分析在不同离轴角θ2下的下行链路的最坏干扰情况。图7为受扰GSO卫星在不同轨位，干扰GSO卫星始终与受扰系统GSO卫星保持3°的轨位间隔条件下的下行链路最坏干扰分布情况。

由图7可知，当受扰卫星位于47°E位置时，此时I/N值最大，最大值为-3.4320 dB，与在37°E分析时的结果相差0.0054 d B，可作为干扰计算分析的精选值。

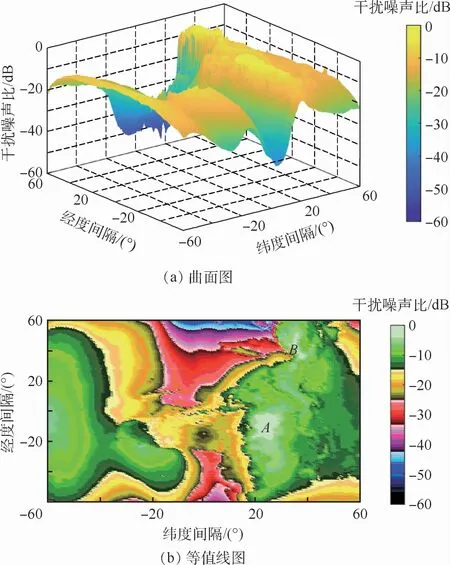
图6 地球站在不同区域分布情况下2颗GSO卫星之间的下行链路I/N曲面图和等值线图Fig.6 Downlink I/N surface map and contour map between two GSO satellites with earth stations in different regions

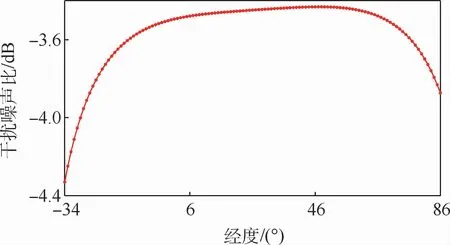
图7 在（23°N，26°E）布设地球站，受扰GSO卫星在不同轨位时的下行链路最坏干扰分布情况Fig.7 The worst interference distribution of downlink interfered GSO satellite at different orbital positions with earth stations deployed at（23°N，26°E）

2 上行链路同频干扰分析方法

2.1 上行链路同频干扰场景构建

对于上行干扰场景而言，本节为了便于描述，在干扰分析时构建的上行干扰场景如图8所示。图中：g′3（θ3）为干扰地球站天线在受扰卫星方向上的发射增益，θ3为干扰地球站发射天线的离轴角；g4（θ4）为受扰卫星天线在干扰地球站方向上的接收增益，θ4为受扰卫星接收天线的离轴角；lei→s为干扰上行链路的传输损耗。

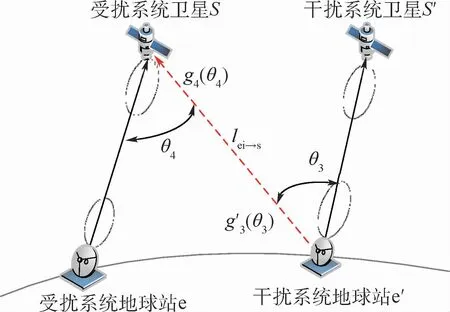
图8 同向上行链路干扰场景Fig.8 Co-directional uplink interference scenario

2.2 上行链路最坏干扰分析

在本节分析过程中，受扰及干扰GSO卫星系统上行干扰场景所使用的波束及空口参数如表2所示，其中地球站天线方向图参考ITU公布的建议书ITU-R S.580-6［15］或者ITU-R S.465-6［16］，星上天线方向图参考建议书ITU-R S.672-4［17］。

利用第1节的结论，受扰及干扰系统地球站在（23°N，26°E）位置附近进行选址，重点分析GSO卫星的分布对同向上行链路I/N值的影响。

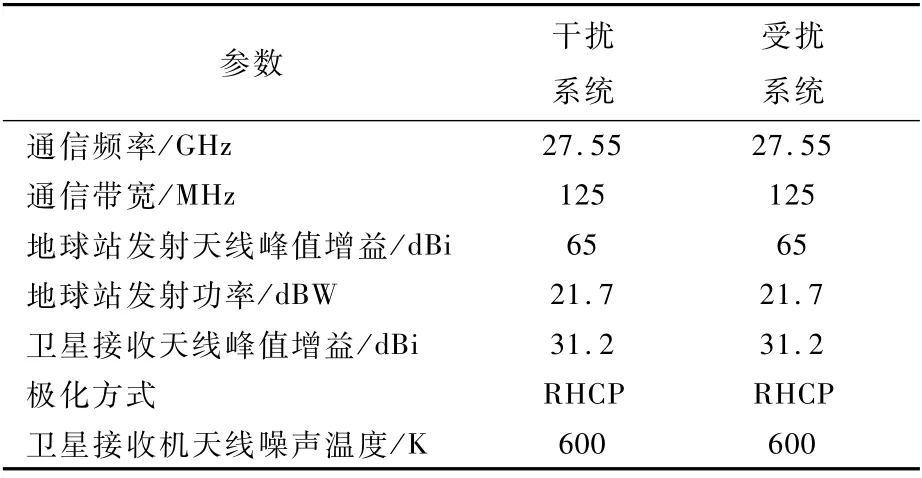
表2 GSO卫星系统上行链路干扰场景波束及空口参数Table 2 Beam and air inter face parameters of GSO satellite system uplink interference scenario

2.3 干扰系统卫星分布对上行I／N计算的影响

分析干扰系统GSO卫星在不同轨位分布情况下2个地球站之间上行链路的I/N，与下行链路分析方法类似，因为受扰GSO卫星和干扰地球站的位置是固定不变的，因此不论干扰系统的GSO卫星如何分布，干扰链路的传输损耗都是一个常量。保持受扰系统GSO卫星（0.1°N，47°E）及其地球站（23°N，29°E）和干扰地球站（23°N，26°E）的位置固定不变，建立干扰系统GSO轨位信息分布族，该分布族是一组独立同分布的随机变量的集合，记作Q：=｛Q1，Q2，…，Qn｝，Qi=［xqi，yqi，zqi］T，i=1，2，…，n，xqi、yqi、zqi为地球固连坐标系下对应于x、y、z轴的位置坐标。上行链路的数学模型函数（I/N）u=g（q）具体为［13］

当θ3=0时，g′3（θ3）取得最大值，即为干扰地球站天线峰值发射增益，此时（I/N）u值最大。

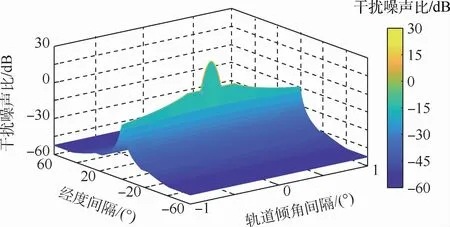
图9 干扰系统GSO卫星在不同轨位下2个地球站之间上行链路的I/N变化曲面图（未包括电波传播损耗）Fig.9 Uplink I/N variation surface map between two earth stations of interference system GSO satellite at different orbital positions（excluding electromagnetic wave propagation loss）

在干扰地球站发射天线的离轴角0.13°＜θ3＜19.95°时，（I/N）u与离轴角θ3的对应关系为

2.4 受扰卫星分布对上行I／N计算的影响

分析受扰GSO卫星在不同轨位分布情况下2个地球站之间上行链路的I/N变化情况，保持受扰卫星系统地球站（23°N，29°E）和干扰地球站（23°N，26°E）的位置固定不变，建立受扰系统GSO轨位信息分布族，该分布族是一组独立同分布的随机变量的集合，记作P：=｛P1，P2，…，Pn｝，Pi=［xpi，ypi，zpi］T，i=1，2，…，n，xpi、ypi、zpi为在地球固连坐标系下对应于x、y、z轴的位置坐标。

图10为在考虑电磁波传播模型前提下，利用2.3节的结论，使干扰系统GSO卫星与受扰系统GSO卫星保持同一轨位，分析GSO卫星在不同轨位下2个地球站之间上行链路的I/N情况。坐标原点代表赤道上空与受扰系统地球站保持同一经度的GSO轨位，坐标轴分别代表与坐标原点之间的轨道倾角间隔和经度差。

由图10可知，在考虑电磁波传播模型前提下，GSO卫星在不同轨位分布情况下2个地球站之间上行链路的干扰噪声比I/N最大值和最小值之间相差1.869 4 dB左右，当受扰和干扰系统GSO卫星与干扰地球站经度相同时干扰最大，且同一经度GSO卫星轨道倾角越大，干扰越大。图11分析了GSO卫星在22°E、24°E、26°E、28°E、30°E时，I/N随轨道倾角的变化情况。

如图11所示，I/N随轨道倾角的变化幅度不大，同一经度上0°轨位倾角和1°轨位倾角间也只相差0.016 5 dB。

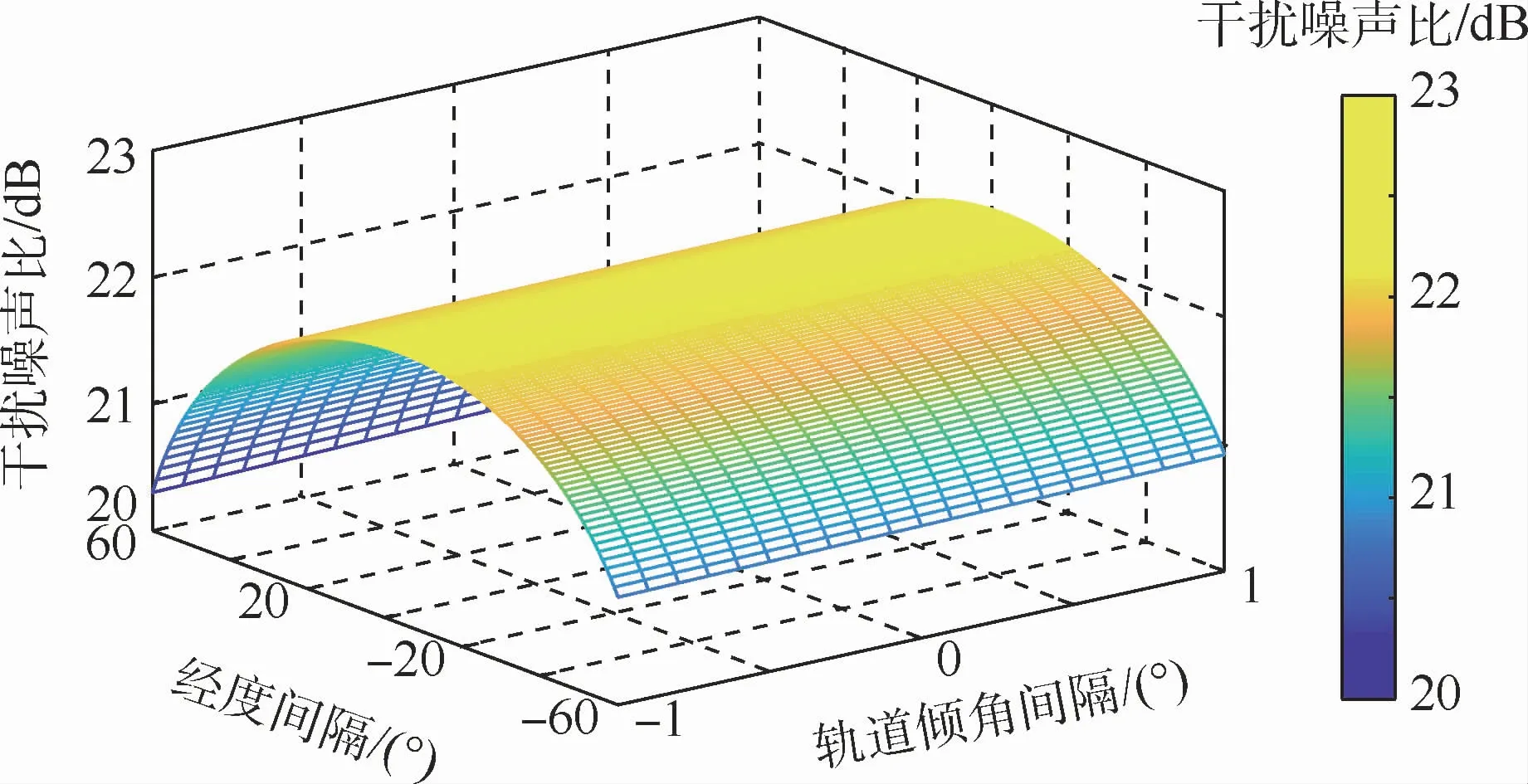
图10 GSO卫星在不同轨位下2个地球站之间上行链路的I/N变化曲面图Fig.10 Uplink I/N variation surface map between two earth stations of GSO satellites at different orbital positions

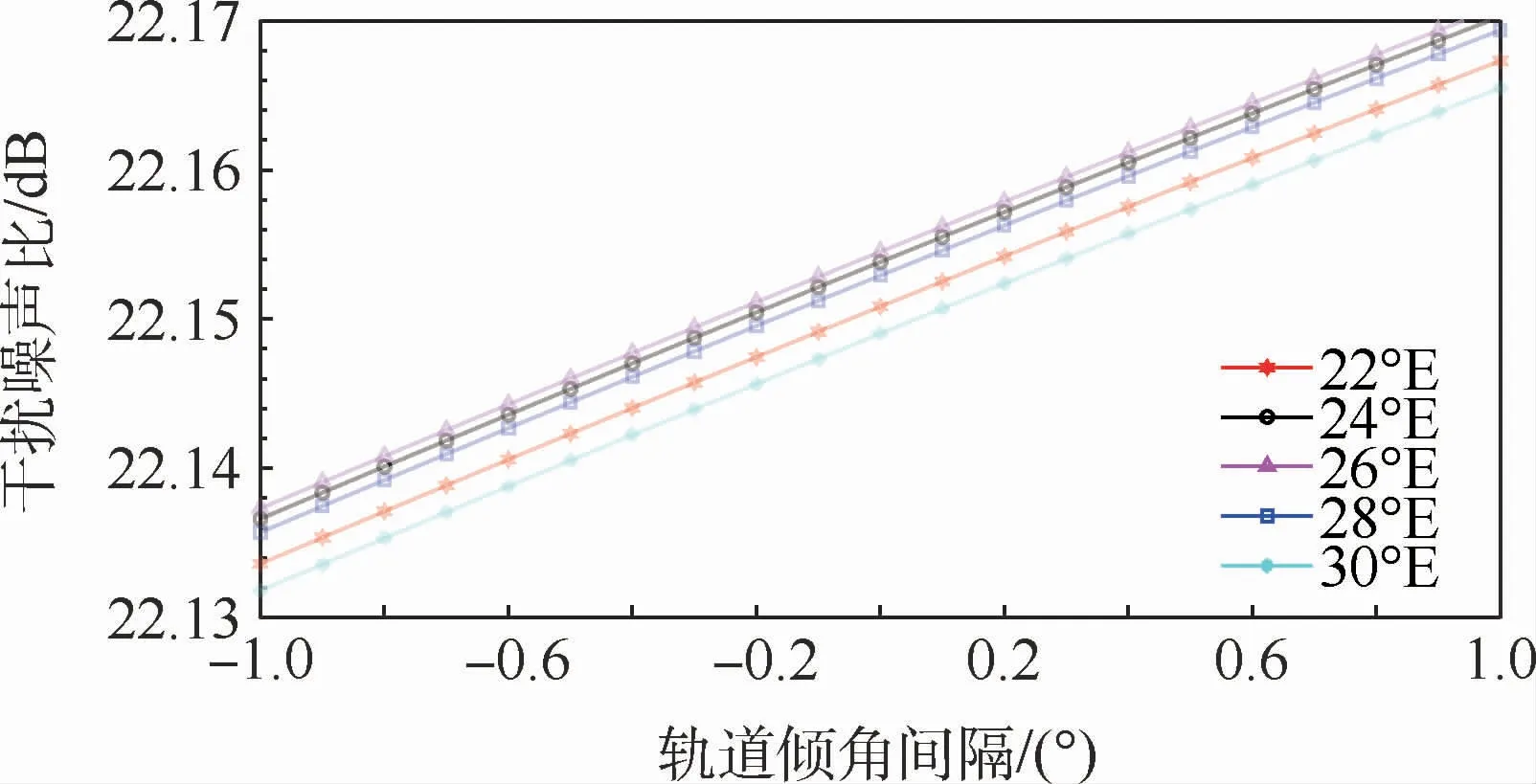
图11 GSO卫星在22°E、24°E、26°E、28°E、30°E时，I/N随轨道倾角的变化曲线Fig.11 Change of I/N with orbital inclination angle of GSO satellite at 22°E，24°E，26°E，28°E and 30°E

3 多波束卫星系统间干扰分析方法

考虑多波束GSO卫星系统间的集总干扰场景，如图12所示，干扰系统卫星S′的点波束数量为m；第i个波束分配到的功率为pi；波束业务需求量为Ti；获得的实际信道容量为Ci。

本节在GSO卫星系统的多个波束之间采用SDMA接入方式，并在该方式的基础上，在波束间采用四色划分的FDMA的多址方式，如图13所示。图中：fi为频率，i=1，2，3，4。

至此，或可理解为何林苍晓老师明知没有先例可循仍屡屡逼迫自己绝境求生，为何创作团队明知难以甚至不可能像之前的作品那样讨得大部分观众的喝彩，却依然要投入更多的心血去把这部作品重新般上舞台。

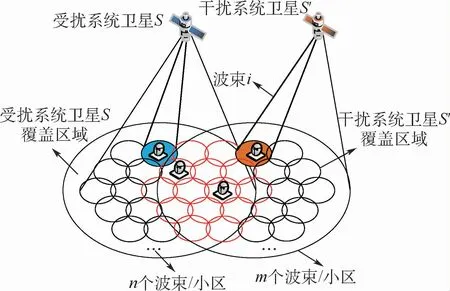
图12 多波束GSO卫星系统间的集总干扰场景Fig.12 Integrated interference scenario between multi-beam GSO satellite systems

图13 四色划分方案Fig.13 Four-color division scheme

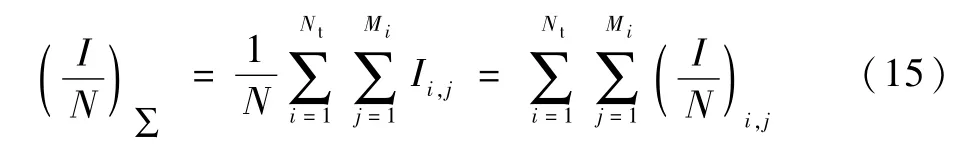
那么受扰GSO卫星系统S接收机接收的集总I/N为式中：Nt为干扰卫星系统S′的发射机总数；Mi为干扰卫星系统S′中第i个发射机的干扰建链总数；N为受扰卫星系统接收机的等效噪声；（I/N）i，j为干扰卫星系统S′第i个发射机建立的第j条干扰链路上的干扰噪声比。

受扰卫星位于47°E轨位，下行链路所使用的波束及空口参数参考1.2节，干扰系统总功率值为30 dBW，总带宽值为125 MHz。考虑到波束间业务需求的不均匀性，假设干扰系统中的第i个波束的业务需求量为80+10（i-1）Mbit/s，采用与受扰系统相同的波束功率分配算法。分析干扰卫星与受扰卫星间隔1°、2°、3°轨位时，在一致功率分配［30-31］、按波束业务需求量公平性功率分配［32］以及基于雨衰补偿的多波束功率分配［23-25，33］3种算法下的集总干扰情况，如图14所示。

图14中，按波束业务需求量公平性分配波束功率相较于其他2种分配方案计算得到的集总干扰I/N值更小。

图14 3种功率分配方案下的多波束卫星系统间的集总干扰Fig.14 Integrated interference between multi-beam satellite systems with three power allocation schemes

4 同向链路典型分析场景

4.1 同向下行链路干扰场景

结合第1节分析结果，参考ITU公布的IFIC数据库，对下行链路干扰场景进行分析，干扰场景评估用例中下行数传参数如表3所示。

在（23°N，26°E）位置布设干扰系统和受扰系统的地球站，在47°E GSO布设受扰系统GSO卫星，波束及空口参数参考表3。可以得到下行链路干扰GSO卫星与受扰系统GSO卫星在不同轨位间隔下干扰噪声比I/N、载波噪声比C/N（C为受扰系统接收到的载波信号功率，W）、载波干扰比C/I、载波噪声干扰比C/（I+N）的变化曲线，如图15所示。

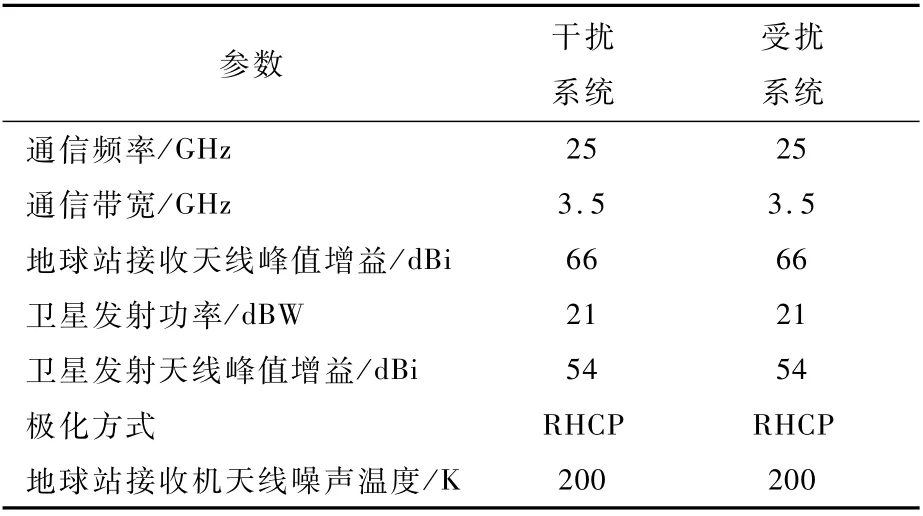
表3 干扰场景评估用例下行数传参数Table 3 Downlink transmission parameters of interference scenario evaluation example

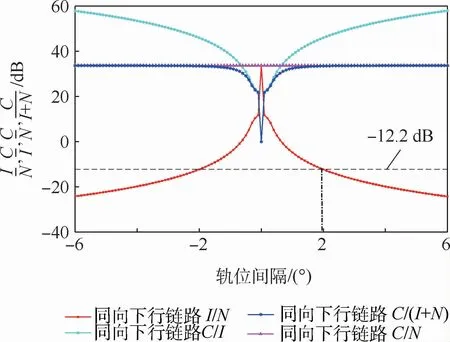
图15 下行链路干扰GSO卫星与受扰系统GSO卫星在不同轨位间隔下I/N、C/N、C/I、C/（I+N）的曲线Fig.15 Curves of I/N，C/N，C/I，C/（I+N）at different orbital intervals between downlink interfering GSO satellites and interfered GSO satellites

在图15中，当卫星轨位间隔为2°时，干扰噪声比I/N为-12.29 dB，当I/N=-12.2 dB时，轨位间隔约为1.95°，该值与ITU建议书中规定的-12.2 dB的限值之间的误差为0.7%，可作为2个GSO卫星系统间干扰评估和规避的参考。

4.2 同向上行链路干扰场景

结合第2节分析结果，参考ITU公布的IFIC数据库，对上行链路干扰场景进行分析，干扰场景评估用例上行数传参数如表4所示。

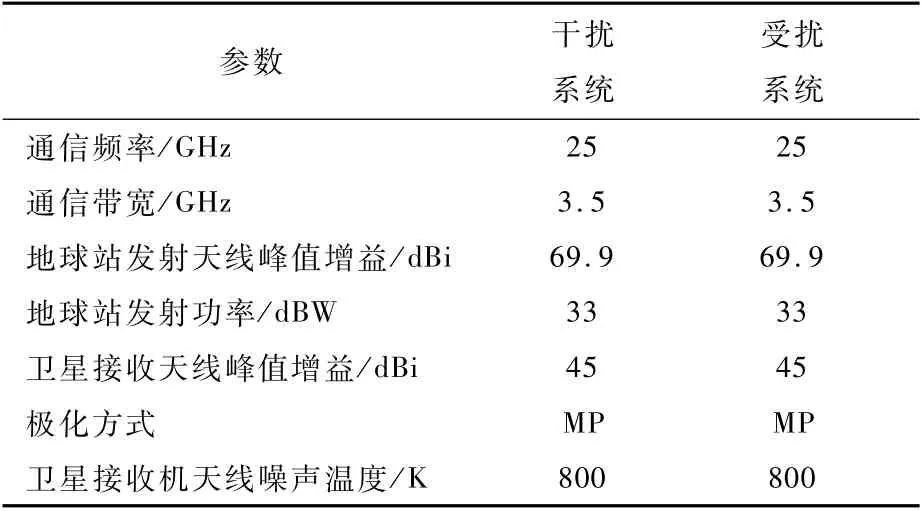
表4 干扰场景评估用例上行数传参数Table 4 Uplink transmission parameters of interference scenario evaluation example

在（23°N，26°E）位置布设干扰系统和受扰系统的地球站，在26°E GSO布设受扰系统GSO卫星，波束及空口参数参考表4。图16为分析上行链路干扰GSO卫星与受扰系统GSO卫星在不同轨位间隔下干扰噪声比I/N、载波噪声比C/N、载波干扰比C/I、载波噪声干扰比C/（I+N）的变化曲线。

图16中，当卫星轨位间隔为2°时，干扰噪声比I/N值为-12.2 dB，这与ITU建议的卫星轨位间隔小于2°时需要协调相符合。可以通过调整天线口径及波束宽度、降低发射功率密度、采用新的信号处理等方式降低卫星系统间的同道干扰。

在轨道倾角为0°，经度为26°E的轨位布设干扰系统和受扰系统的GSO卫星，在（23°N，26°E）布设受扰系统地球站，波束及空口参数参考表4。可以计算出上行链路干扰地球站在与受扰系统地球站在不同经纬度间隔下I/N的变化曲线，如图17所示，坐标轴分别表示与受扰系统地球站的经纬度差值。

图16 上行链路干扰GSO卫星与受扰系统GSO卫星在不同轨位间隔下I/N、C/N、C/I、C/（I+N）的曲线Fig.16 Curves of I/N，C/N，C/I，C/（I+N）at different orbital intervals between uplink interference GSO satellites and interfered systems GSO satellites

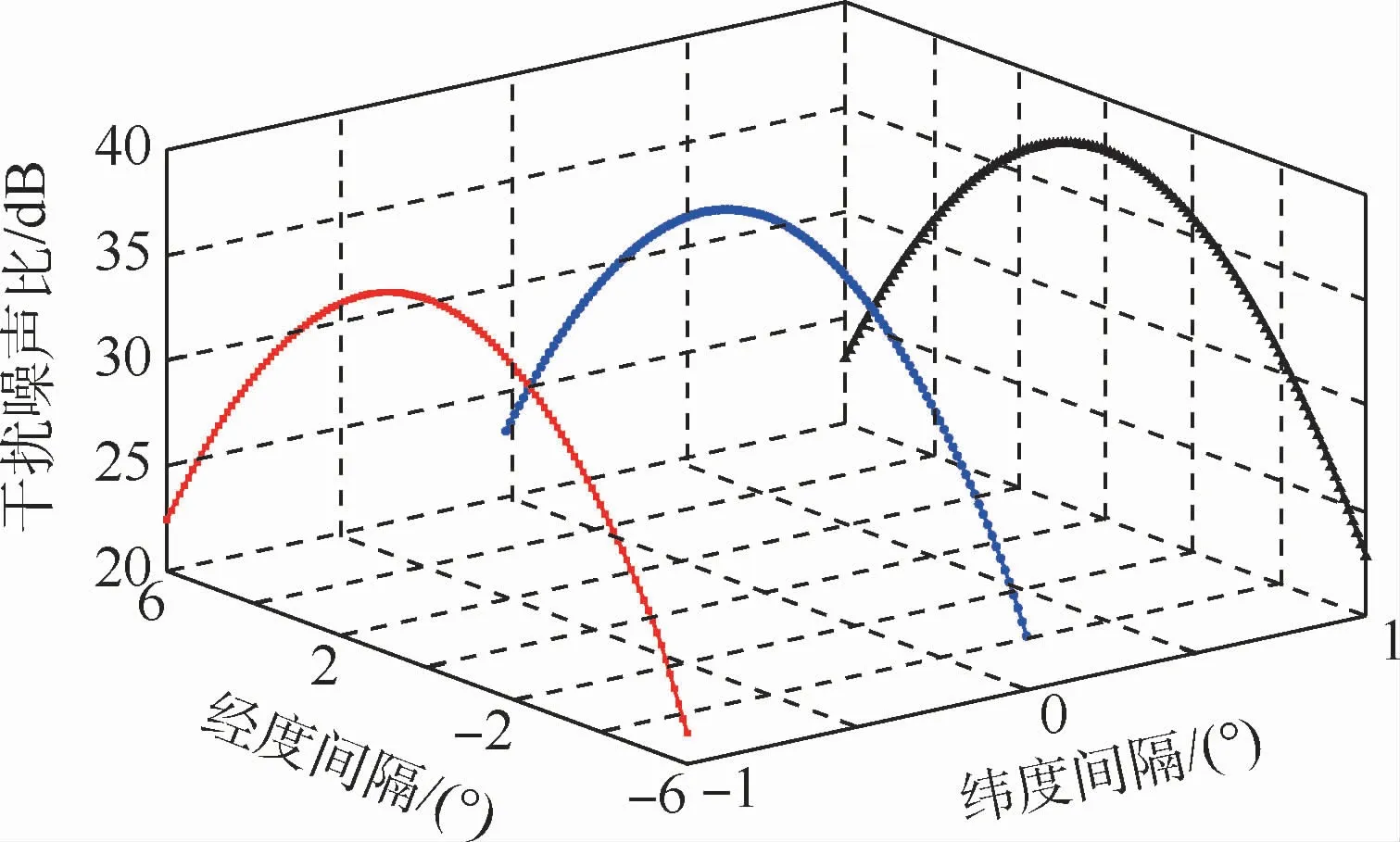
图17 上行链路干扰地球站与受扰系统地球站在不同经纬度间隔下I/N的曲线Fig.17 Curves of I/N with uplink interfering earth station and interfered systems earth station at different latitude and longitude intervals

由图17可知，可以得出当2颗GSO卫星轨位几乎重合时，仅采用小幅度调整地球站位置的方式很难规避卫星系统间的干扰。

5 反向链路典型分析场景

在本节中只讨论受扰系统为上行链路，干扰系统为下行链路的情况，构建的干扰场景如图18所示，lsi→s为星间通信链路的传输损耗。

选取表4受扰系统上行参数和表3干扰系统下行参数来进行反向上行链路分析。在（23°N，26°E）布设受扰系统地球站，干扰系统地球站与其重叠，受扰GSO卫星轨位为26°E的地球静止轨道，分析干扰GSO卫星与受扰GSO卫星在不同轨位间隔下干扰噪声比I/N、载波噪声比C/N、载波干扰比C/I、载波噪声干扰比C/（I+N）的变化曲线，如图19所示。

在反向链路干扰分析中，即使来自轨位间隔为2°的卫星对受扰系统的影响也未超过-20 d B。

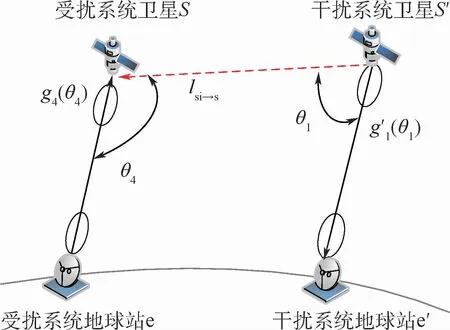
图18 反向上行链路干扰场景Fig.18 Reverse uplink interference scenario

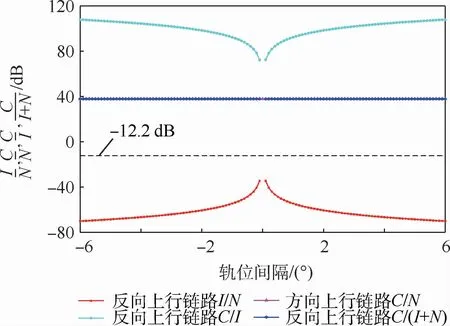
图19 反向链路干扰GSO卫星与受扰GSO卫星在不同轨位间隔下I/N、C/N、C/I、C/（I+N）的变化曲线Fig.19 Curves of reverse link I/N，C/N，C/I，C/（I+N）with interfering GSO satellite and interfered GSO satellite at different orbital intervals

6 结 论

为了解决GSO卫星系统间在卫星和地球站布设中的同频干扰评估问题，基于不同布设场景下卫星系统间的干扰分布情况，构建了对应的干扰评估和分析计算的模型。

1）提出了一种基于干扰函数极值的评估方法，并结合ITU提供的全球地形数据、天线波束参数、电磁波传播模型，定量化计算了卫星轨位和地球站布设对干扰评估的影响情况，明确了其对应的最坏取值及干扰评估的条件和变化趋势。

2）分析了一致功率分配、按波束业务需求量公平性功率分配以及基于雨衰补偿的多波束功率分配3种算法对多条链路集总干扰的影响，在相同的波束条件下，按波束业务需求量公平性分配波束功率相较于其他2种分配方案计算得到的集总I/N值更小。

3）计算结果与ITU建议书中规定的限值之间的误差为0.7%（2°轨位间隔），证明了该方法的可行性与有效性，可作为2个GSO卫星系统间干扰评估和规避措施制定的参考。