基于瞬时相关频域检测的复合调制引信定距方法

王雄武，郝新红，*，贾建光，栗苹，陈齐乐

（1.北京理工大学 机电动态控制重点实验室，北京100081；2.中国人民解放军军事科学院 系统工程研究院，北京100091）

常规对地无线电引信以地面为目标，回波能量与地面散射系数成正比。地面散射系数与地面类型、落角等因素有关，引信面对不同散射特性的地面，回波能量差别很大［1-2］。伪码调相与线性调频复合调制引信［3］采用基于自相关函数包络检测［4-5］方法实现定距，回波能量不同将会带来2个问题：①针对不同地面目标需要设置不同的幅值判决门限；②地面散射系数太小时回波信号中信噪比过低，很难正确地检测出目标。

针对不同回波能量下的判决门限问题，引信中一般采用恒虚警检测算法［6-7］设置自适应门限。为了提高回波信号的信噪比，可以采用自适应滤波［8］、小波降噪［9-10］等算法。但是，这些复杂算法以大幅增加引信资源占用量为代价，在引信小体积平台上难以满足实时性要求。

混沌码不仅具有和伪随机码一样优良的相关特性，还具有伪随机码不具备的初值敏感性、长周期性等优势。与伪随机码相比，以混沌码作为调制序列的引信信号具有更好的低截获性能与抗干扰性能［11］。本文结合混沌调相与线性调频复合调制无线电引信（下文简称复合引信）目标回波信号时频域特征，提出了一种基于瞬时相关频域检测的复合引信定距方法。时域上利用本地预设混沌码对目标回波信号进行瞬时相关处理，频域上采用二维快速傅里叶变换（2D-FFT）算法提取目标距离、速度信息，以相关窗位置、谐波包络主瓣位置、稳定的多普勒频率3个特征量为定距依据，可以在牺牲较少的资源占用量的情况下实现复合引信在不同回波能量下的精确定距。

1 复合引信模型

复合引信工作原理如图1所示。三角波线性调频信号经定向耦合后输出两路，一路作为本地参考信号，一路经混沌码调相后通过收发共用天线发射出去。目标回波信号与本地参考信号经混频、滤波后，得到包含目标距离与速度信息的复合引信差频信号，其表现为回波混沌码与线性调频引信（LFM）差频信号的乘积。利用本地预设混沌码在时域上对此信号进行瞬时相关处理，得到瞬时相关差频信号uc（t），幅值归一化后可表示为

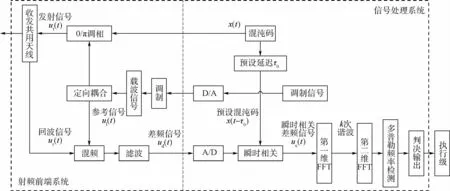
图1 混沌调相与线性调频复合引信工作原理Fig.1 Working principle of hybrid modulation fuze combining chaotic code bi-phasemodulation with linear frequency modulation

由于m（t）为Rx（τ0-τ）的被积分项，称m（t）为混沌码瞬时相关信号。当2个混沌码存在重叠时，重叠部分瞬时相关结果为常数1，此时称两混沌码相关。同时，将目标回波混沌码与本地预设混沌码相关时弹目距离的范围称为相关窗Rc。

由频域卷积定理可知，uc（t）在频域上表现为混沌码瞬时相关信号频谱与LFM 差频信号频谱的卷积：

式中：F［·］为傅里叶正变换。三角波线性调频差频信号频谱表现为各次谐波谱线，谐波幅值为受目标多普勒信号幅度调制的sinc函数［12］：

式中：a（k，τ）为各次谐波幅值，k为谐波次数；sinc x=sin x/x；Tm为调制周期；fm=1/Tm为调制频率；β=4ΔF/Tm为调制率，ΔF为调制频偏；fd为目标多普勒频率。

实际弹目交会过程中，弹体的速率与落角会散布在一定范围，因此目标多普勒频率存在范围［fdmin，fdmax］。分析式（1）、式（4）可知，当目标回波混沌码与本地预设混沌码完全相关时，uc（t）中只存在LFM差频信号，根据某次谐波幅值中的目标多普勒信号，利用2D-FFT算法提取其中的距离、速度信息，进行目标识别后在预定炸点处判决输出，即可实现复合引信的精确定距。

2 基于瞬时相关频域检测的定距方法设计

基于瞬时相关频域检测的定距方法可分为3个步骤：

步骤1 在进行时域瞬时相关之前，对式（2）表示的混沌码瞬时相关信号中的回波混沌码、预设混沌码进行同步采样，采样周期等于码元宽度。

步骤2 控制相关窗右边界对应距离与某次谐波主瓣右边界对应距离重合。

步骤3 采用2D-FFT算法提取瞬时相关差频信号uc（t）中的多普勒信息，当多普勒频率稳定出现在目标多普勒频率范围内时判定出现目标信息，通过相关窗位置、谐波包络主瓣位置和目标多普勒频率3个特征量提取目标的距离、速度信息，完成对目标的精确、可靠定距。

2.1 采样策略选定

在数字系统中，数据以采样点的形式存储，离散采样点可以理解为维持一个采样周期的连续时间信号。采用不同的策略对回波混沌码、预设混沌码进行采样，得到的混沌码瞬时相关信号千变万化。为了简化混沌码瞬时相关信号，减小其在相关窗内对uc（t）的影响，本文对上述2种码信号以码元宽度Tc为采样周期进行同步采样，并规定：

1）零时刻为第一个采样时刻。

2）采样点为采样时刻左极限处的信号数据。

这样，回波混沌码的采样信号，即回波采样码，具有明确的解析形式：

可以得到对应相关窗的范围。

对回波混沌码与预设混沌码以码元宽度为采样周期进行同步采样后，m（t）只存在2种状态：相关窗内的完全相关态与相关窗外的完全不相关态。在此种采样策略下，uc（t）在相关窗外为LFM差频信号与一个伪随机码的乘积，其频谱为类噪声谱，各次谐波幅值为低能量噪声；在相关窗内为单纯LFM差频信号，各次谐波幅值为受目标多普勒信号幅度调制的sinc函数。多普勒频率在相关窗内外有明显差别，为从频域角度实现复合引信的定距提供了可能。

2.2 相关窗位置控制

以三角波调制的LFM 差频信号其k次谐波包络主瓣范围为

在确定了码元宽度Tc、调制频偏ΔF、谐波次数k等系统参数后，只需调整系统附加延迟τsc与本地预设延迟τ0，即可实现相关窗位置的控制。

2.3 定距方法设计

图2为本文设计的定距方法流程，其基本思路为：

1）利用2D-FFT［14-15］算法提取多普勒频率。将瞬时相关差频信号每调制周期时间长度作为一帧数据进行距离维FFT，取出其中k次谐波的幅值信息；将k次谐波幅值作为输入信号进行速度维FFT，以得到的频谱能量峰值点对应频率作为多普勒频率。

图2 复合引信定距方法流程图Fig.2 Flowchart of ranging method based on hybridmodulation fuze

作为目标判定条件，当累加距离值满足式（12）时输出点火信号。

定距方法对应参数与它们的约束条件如下：

1）距离维FFT每帧数据点数NT1。对瞬时相关差频信号进行单周期FFT运算时，取一个调制周期长度Tm的数据作为一帧数据，即

3）速度维FFT帧间更新点数ND2和判定点数NL。速度维FFT每一个输入数据点代表的目标信号时间长度为调制周期Tm，故参与判定的目标信号时间长度为（NT2+NLND2）Tm。因此，判定距离RL与判定点数NL存在如下关系：

2.4 定距精度与测速精度

3 仿真分析与讨论

搭建复合引信Simulink模型进行系统仿真，参数设置如表1所示。设定速度维FFT频率分辨率Δf2=1 kHz，则可计算出定距方法中的参数，如表2所示。

表1 复合引信仿真参数取值Table 1 Simulation parameter values of hybrid modulation fuze

表2 定距方法参数取值Table 2 Parameter values of ranging method

3.1 瞬时相关混沌码频谱

根据式（8）与表1、表2中相关参数，可得完全相关时目标回波延迟τ的范围为［0，50）ns。分别在目标回波延迟τ=30 ns、τ=80 ns时刻下得到的瞬时相关混沌码频谱如图3所示。当τ=30 ns时，回波采样码与预设采样码完全相关，瞬时相关混沌码为常数1，其频谱为零频处的冲激函数，如图3（a）所示；当τ=80 ns时，回波采样码与预设采样码完全不相关，瞬时相关混沌码为一伪随机码，其码元宽度与原混沌码一致，频谱表现为带宽为1/Tc的低能量宽谱特性，如图3（b）所示。

此仿真结果验证了2.1节中的分析。因此，在弹目不断接近的过程中，目标回波延迟τ不断减小，当弹目距离在相关窗外时，瞬时相关混沌码为一伪随机码；当弹目距离在相关窗内时，瞬时相关混沌码为常数1。

图3 不同目标回波延迟下瞬时相关混沌码频谱Fig.3 Spectrums of instant correlation chaos code under different target echo delays

3.2 瞬时相关差频信号特征

分别截取相关窗内外的瞬时相关差频信号进行频谱分析，结果如图4所示。在相关窗内，其频谱与LFM差频信号频谱一致，表现为高能量的谱线特性，如图4（a）所示；在相关窗外，其频谱受伪随机码频谱的影响表现为低能量宽谱特性，从中体现不出LFM差频信号的频谱特性，如图4（b）所示。

图4 相关窗内外瞬时相关差频信号频谱Fig.4 Spectrums of instant correlation beat signal inside/outside correlation window

采用2D-FFT算法提取瞬时相关差频信号中的某次谐波包络与多普勒频率特征，从而得到目标的距离、速度信息。图5分别为LFM 引信16次谐波幅值、复合引信16次谐波幅值、复合引信多普勒频率与距离的关系曲线。结果显示，在相关窗内外复合引信谐波时频域特征有明显差异：在相关窗外，16次谐波幅值为低能量噪声，多普勒频率杂乱无章；在相关窗内，16次谐波幅值与LFM引信16次谐波幅值一致，存在明显sinc包络且多普勒频率稳定在目标多普勒频率处。

在目标回波中加入加性高斯白噪声，在SNR=0 d B条件下给出了2种不同地面散射系数σ0下的目标判定结果如图6所示。仿真结果表明，相同信噪比下，回波能量对多普勒频率基本没有影响。

3.3 定距方法

控制引信开机时弹目起始位置在［11，13］m范围内，在SNR=0 dB、5种不同地面散射系数条件下依次进行500次蒙特卡罗实验，得到如图7所示判定距离箱线图。可以看到，5组判定结果完全一致，判定结果只与目标回波信号的信噪比有关，而与信号幅值具体大小无关。

图5 复合引信谐波幅值、多普勒频率与距离的关系Fig.5 Relationship between harmonic amplitude&Doppler frequency and range for hybrid modulation fuze

在地面散射系数σ0=0 dB、不同信噪比条件下进行2 000次蒙特卡罗实验，得到的判定距离箱线图如图8所示。将判定距离在（R0-ΔR，R0+ΔR）范围内认定为定距成功，得到各信噪比条件下定距成功率如表3所示。结果表明，定距方法在SNR=-28 dB的极低信噪比下定距成功率仍有99.25%。

综合以上仿真分析，只需保证目标回波信号的信噪比不低于-28 dB，本文提出的基于瞬时相关频域检测定距方法在面对不同散射特性地面目标时均能实现复合引信的精确、可靠定距。

图6 不同地面散射系数下多普勒频率及目标判定结果Fig.6 Doppler frequency and target judgment results under different ground scattering coefficients

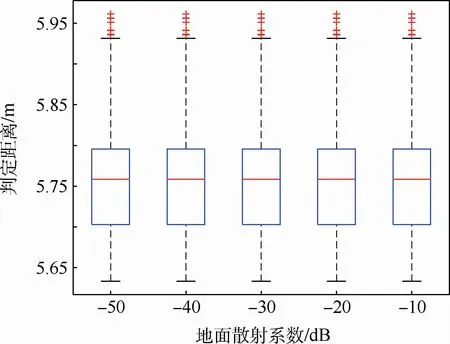
图7 不同地面散射系数下判定距离箱线图Fig.7 Box-plot of judging ranges under different ground scattering coefficients

图8 不同信噪比下判定距离箱线图Fig.8 Box-plot of judging ranges under different signal-to-noise ratios

表3 不同信噪比下定距成功率Table 3 Ranging success rates under different signal-to-noise ratios

4 结 论

本文针对混沌调相与线性调频复合调制引信，提出一种适应不同散射特性地面目标的基于瞬时相关频域检测定距方法，得出如下结论：

1）对本地预设混沌码与目标回波信号中的混沌码以码元宽度为采样周期进行同步采样后，瞬时相关差频信号只存在2种状态：相关窗内的完全相关状态与相关窗外的完全不相关状态。

2）复合引信瞬时相关差频信号特征在相关窗内外存在明显差别，在相关窗外为低能量噪声，在相关窗内为LFM差频信号；相关窗内的谐波包络中存在目标的距离、速度信息，灵活调整相关窗的位置即可控制目标信息出现的时间。

3）基于瞬时相关频域检测的定距方法判定结果只与目标回波信号的信噪比有关，而与信号幅值具体大小无关；在SNR=-28 dB的极低信噪比条件下能够实现复合引信对不同散射特性地面目标的精确定距功能。