The Uniform Boundedness and Convergence for the Core Inverses of Linear Operators in Banach Spaces

ZHAO Yayuan(赵亚媛)，CHEN Saijie(陈赛杰)ZHU Lanping(朱兰萍)，HUANG Qianglian(黄强联)

(School of Mathematical Sciences，Yangzhou University，Yangzhou 225002，China)

Abstract: The main topic of this paper is the relationship between uniform boundedness and convergence of the core inverses of linear operators in Banach spaces.We first obtain the equivalence of the uniform boundedness and convergence for core inverse and we give the expression of core inverse.Secondly，we investigate the stable perturbation for the core inverse and prove that the stable perturbation and the continuity of the core inverse are equivalent.As applications，we also give the continuity characterization for the core inverse of finite rank operators and derive the sufficient and necessary condition for the core inverse of the perturbed operator to have the simplest possible expression.

Key words: Core inverses; Uniform boundedness; Convergence; Generalized inverse;Stable perturbation

1.Introduction and Preliminaries

Let X，Y be Banach spaces and B(X，Y) denote the Banach space of all bounded linear operators from X into Y.We write B(X) as B(X，X).For any T ∈B(X，Y)，we denote the null space and the range of T by N(T) and R(T)，respectively.The identity operator will be denoted by I.

Recall that an operator S ∈B(Y，X) is said to be a generalized inverse of T ∈B(X，Y)if S satisfies:

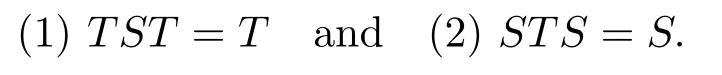
A generalized inverse of T is usually denoted by T+.While the generalized inverse may not exist and it is not unique even if it exists.In order to force its uniqueness，some further conditions have to be imposed.Let us recall definitions of three important generalized inverses.

Definition 1.1Let X and Y be Hilbert spaces.An operator S ∈B(Y，X) is called the Moore-Penrose inverse of T ∈B(X，Y) if S satisfies the Penrose equations:

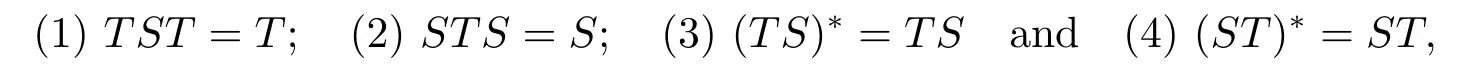
where T*denotes the adjoint operator of T.The Moore-Penrose inverse of T is always written by T†，which is uniquely determined if it exists.

Definition 1.2Let X be a Banach space.An operator S ∈B(X) is said to be the group inverse of T ∈B(X)，always denoted by T♯，if S satisfies

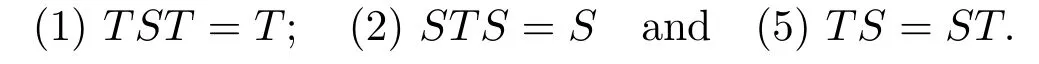
The core inverse is a generalized inverse somehow between the Moore-Penrose inverse and the group inverse，which was introduced by Baksalary and Trenkler for the matrix T satisfying Rank T2=Rank T♯.In [2]，Raki´c，Dinˇci´c and Djordjevi´c extended it to the operator on a Hilbert space:

Definition 1.3[2]Let X be a Hilbert space.An operator S ∈B(X) is said to be the core inverse of T ∈B(X)，denoted by T，if S satisfies

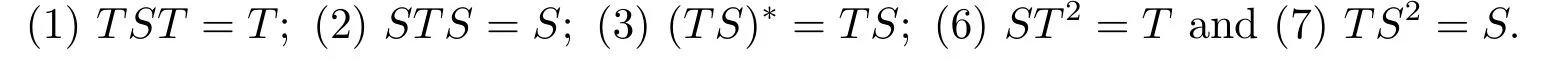
For the invertible operator，by the well known Banach Lemma and the identity:

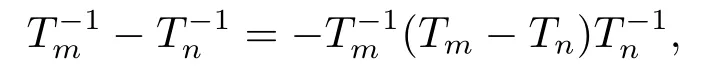
we can get the following theorems.

Theorem 1.1Let T ∈B(X，Y) be invertible and T-1its inverse.If Tn∈B(X，Y)satisfies Tn→T，then there exists N ∈N，such that for all n ≥N，Tnis invertible and

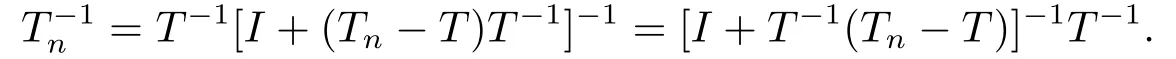
Theorem 1.2Let Tnand T ∈B(X，Y) satisfy Tn→T.If Tnis invertible andthen T is invertible and

Hence we can claim that T is invertible if and only if Tnis invertible with+∞，in this case，It is natural to ask whether similar results hold for various generalized inverses.Such problems of expression，boundedness and convergence have been investigated for the generalized inverse in [3-11]，the Moore-Penrose inverse in [6-8，11-15]，the group inverse in [3，8，11，16-18] and the core inverse in [1，2，19].Especially，Koliha[14]，ZHU，ZHU and HUANG[11]proved the equivalence between the uniform boundedness and convergence for the Moore-Penrose inverse and group inverse，respectively.

In this paper，we shall investigate the same problems for the core inverse.By utilizing the stable perturbation，we obtain the equivalence of the uniform boundedness and convergence for core inverse and some expression results.For the stable perturbation of the generalized inverse，we have the following theorem which plays a crucial role in our proof.

Theorem 1.3[8]Let X and Y be Banach spaces and T+∈B(Y，X) be a generalized inverse of T ∈B(X，Y).Assume that I +δTT+: Y →Y be bijective with δT ∈B(X，Y).Then the following statements are equivalent:

1) B =T+(I+δTT+)-1=(I+T+δT)-1T+is a generalized inverse of=T +δT;

In the next section，we first prove that T is core invertible if and only if Tnis core invertible withand give a concrete expression of T.Secondly，we prove the equivalence between the stable perturbation and the continuity for the core inverse.As applications，we also derive the continuity characterization for the core inverse of finite rank operators and the characterization for the core inverse of the perturbed operator to have the simplest possible expression.For the null space-preserving or the dimension of null spacepreserving perturbation，we give a complete answer to the problem proposed in [19].

2.Main Results

As mentioned above，an operator T is invertible if and only if Tnis invertible withIt turns out that the same property is also enjoyed by the core inverse.

Theorem 2.1Let X be a Hilbert space and Tn，T ∈B(X) with Tn→T.If the core

2) T has the core inverse Tsatisfying

In this case，for all sufficiently large n，

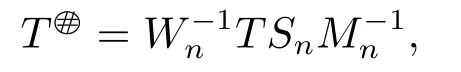
ProofIt is obvious to see 2)⇒1)and we only need to prove 1)⇒2).By the definition of the core inverse，we can get

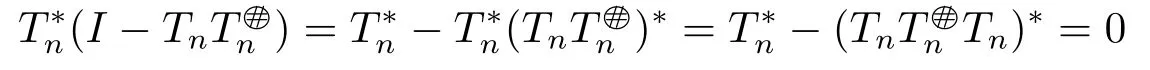
and

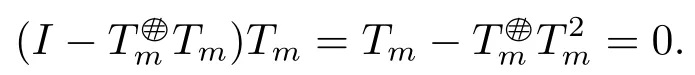
By the Banach Lemma，I +(T -Tn)is invertible.Therefore，

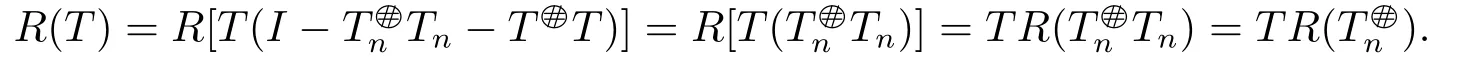
Since I+(T -Tn)is invertible，from Theorem 1.3，

is a generalized inverse of T.Observing that

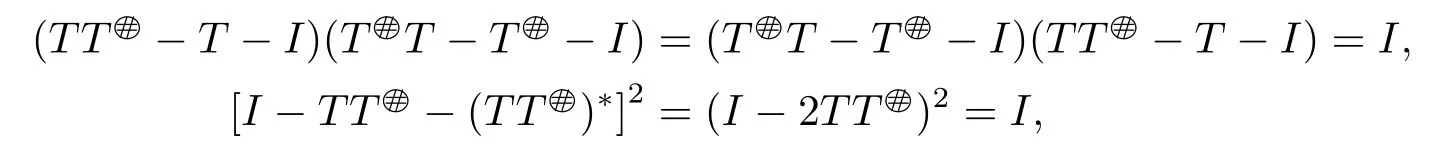
and

we know that for all sufficiently large n，Wn=TSn-T -I and Mn=I-TSn-(TSn)*are invertible.To complete the proof，we shall show that

is the core inverse of T.In fact，=Mnand if we set Qn=TSn，then

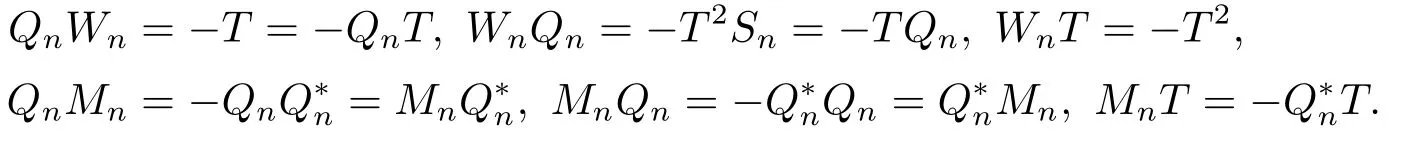
Hence

Thus，by the definition of Vn，

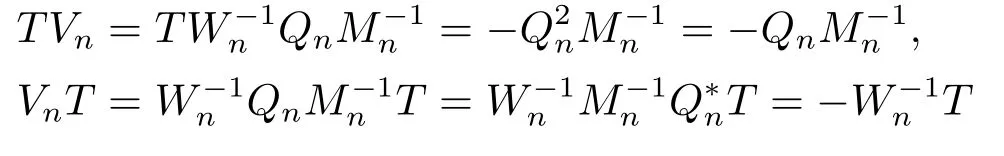
and so

Therefore，Vnis a generalized inverse of T and

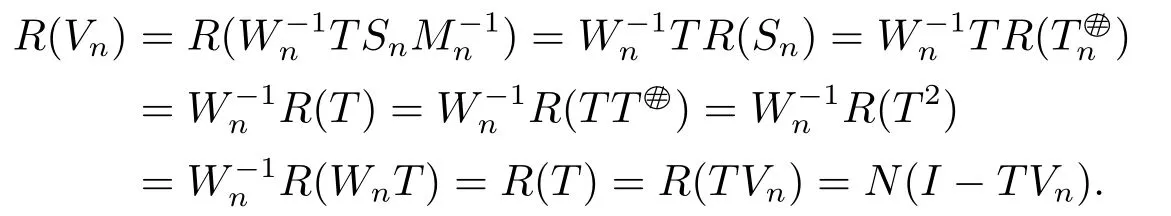
This imples (I-TVn)Vn=0 and so=Vn.Thus，Vnis the core inverse of T.The proof is complete.

Theorem 2.1 provides a sufficient and necessary condition for the core invertibility of Tnto imply the core invertibility of T and→T.Naturally，we can propose the following problems: Can the core invertibility of T imply the core invertibility of Tn? If Tnis also core invertible，does the core inverseconverge or→T? The following two examples show that the answers are no in general.

Example 2.1Let

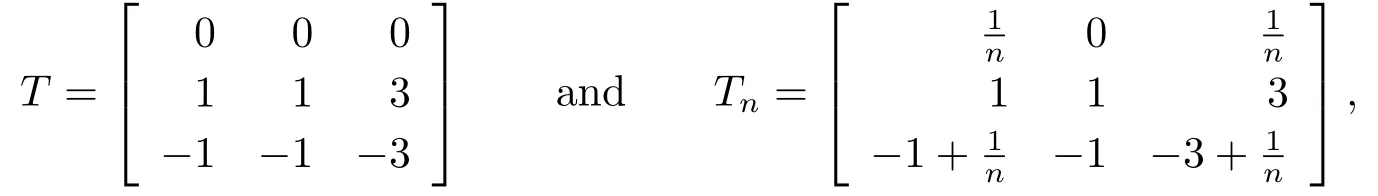
then Tn→T and T is core invertible with

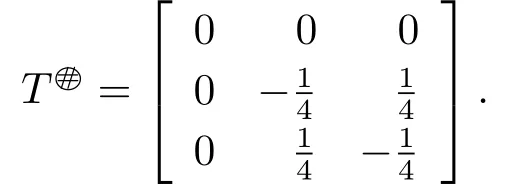
But Tnis not core invertible since Rank Tn=2 and Rank=1.

Example 2.2Let

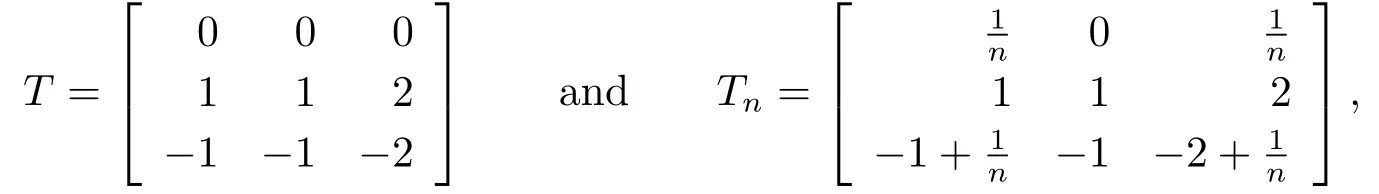
then Tn→T，both T and Tnare core invertible with

The next theorem shows that if T is core invertible，then Tnis core invertible with→if and only if Tnis a stable perturbation of T.Moreover，a concrete expression ofis also obtained.

Theorem 2.2Let X be a Hilbert space and T ∈B(X) be core invertible.Let Tn∈B(X) satisfy Tn→T，then the following statements are equivalent:

1) For all sufficiently large n，Tnis a stable perturbation of T，i.e.，

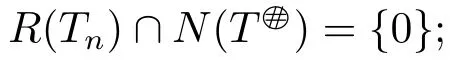
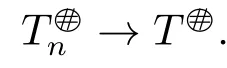
2) There exists N ∈N，such that for all n ≥N，Tnis core invertible with

In this case，for all sufficiently large n，

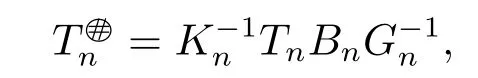
where Bn=T[I+(Tn-T)T]-1，Kn=TnBn-Tn-I and Gn=I-TnBn-(TnBn)*.

Proof1)⇒2) It follows from Theorem 1.3 that，for all sufficiently large n，I+(Tn-T)T#○is invertible and

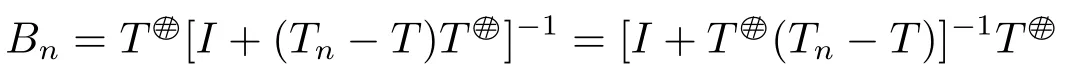
is a generalized inverse of Tn.Similar to the proof of Theorem 2.1，we can prove that for all sufficiently large n，

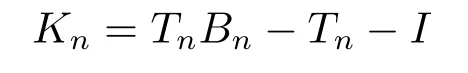
and

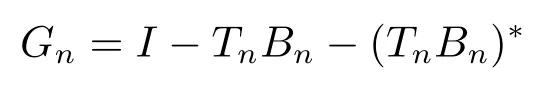
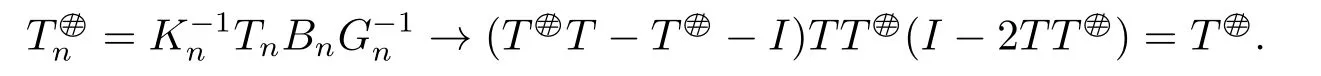
2)⇒1) For all sufficiently large n，we know that bothandTT are invertible，and

By Theorem 1.3，we get R(Tn)∩N(T#○)={0}.The proof is complete.

As an application，we can give a characterization that Tnis core invertible withfor finite rank operators.

Corollary 2.1Let T ∈B(X) be of finite rank.If Tn→T and T is core invertible，then the following statements are equivalent:

1) Rank Tn= Rank T for all sufficiently large n;

2) There exists N ∈N，such that for all n ≥N，Tnis core invertible with

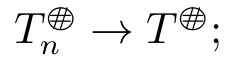
3) There exists N ∈N，such that for all n ≥N，Tnis core invertible with

In this case，

ProofIt suffices to prove 1) ⇔2).Without loss of generality，we can assume thatis invertible.It follows from

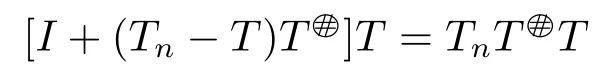
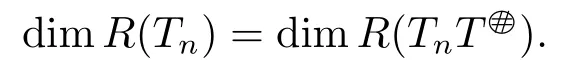
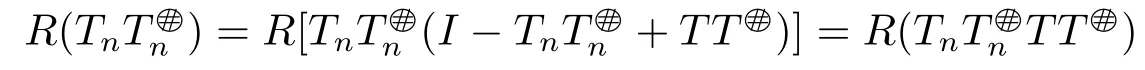
and

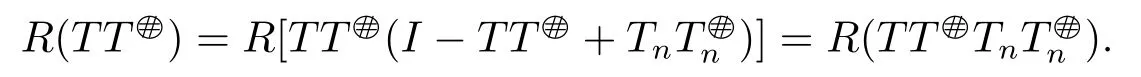
The proof is complete.

It is also noteworthy that we provide a direct and brief proof in Corollary 2.1 and we do not use the Finite Rank Theorem[9].Next，we can give the characterization for the core inverseto have the simplest possible expression.

Corollary 2.2Let X be a Hilbert space and T ∈B(X)be core invertible.If Tn∈B(X)satisfies Tn→T，then for all sufficiently large n，Tnis core invertible and

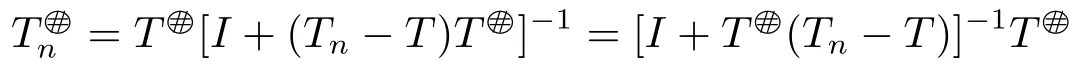
if and only if Tn=TTTn.

ProofSufficiency.Ifthen R(Tn)⊂R(T) and

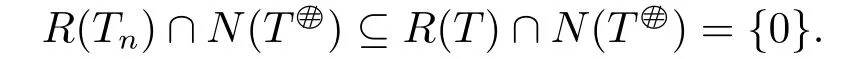
we can get [I-TnBn-(TnBn)*]2=(I-2TT2=I and

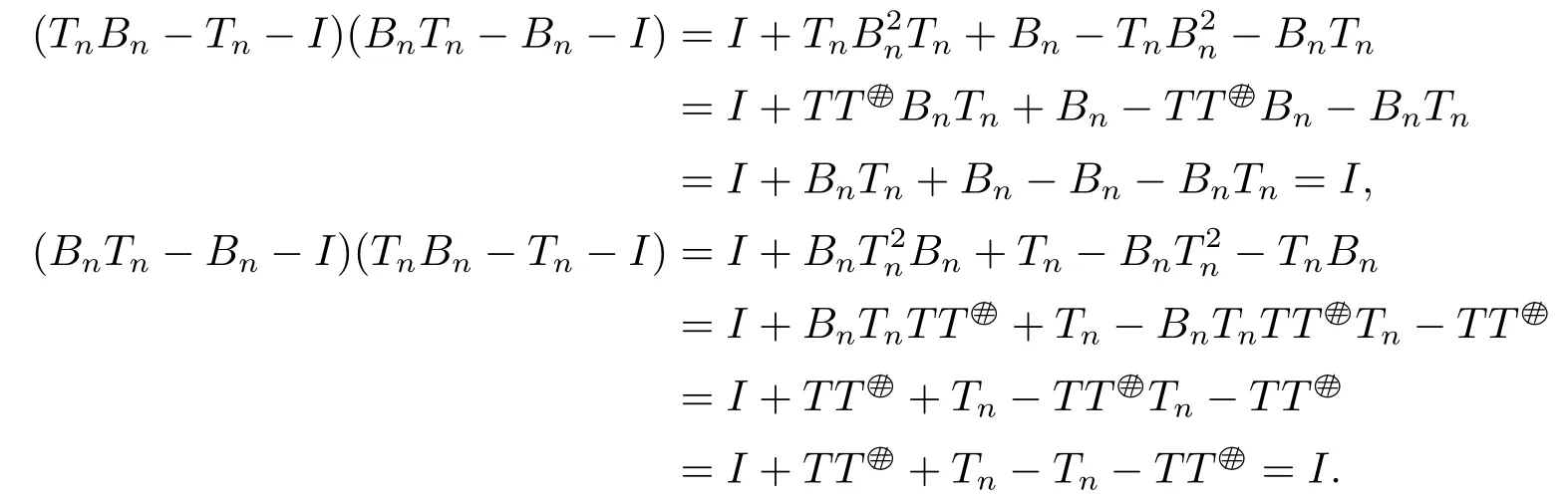
Hence[I-TnBn-(TnBn)*]-1=I-2TTand(TnBn-Tn-I)-1=BnTn-Bn-I.Therefore，by Theorem 2.2，we have

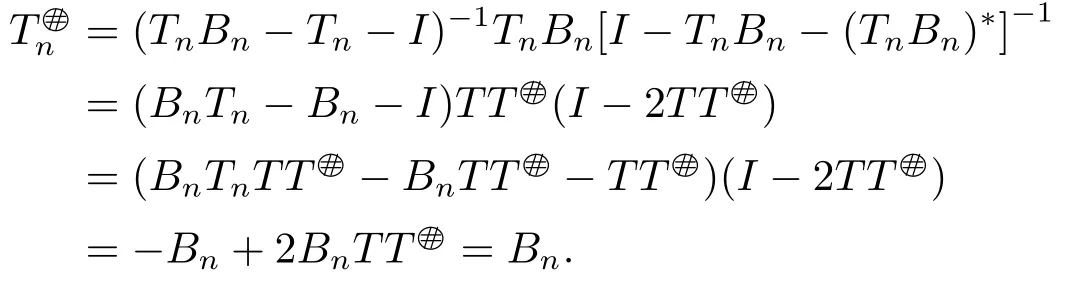
Necessity.If Bnis the core inverse of Tn，then

This means (I -TT)Tn=0，i.e.，Tn=TTTn.The proof is complete.

Since both the null space-preserving perturbation and the dimension of null spacepreserving perturbation are all stable perturbations[6-7]，we can get the following corollary which gives a complete answer to the problem proposed in [19].

Corollary 2.3Let X be a Hilbert space.Let T ∈B(X)with its core inverse T∈B(X)and Tn∈B(X) with Tn→T.If

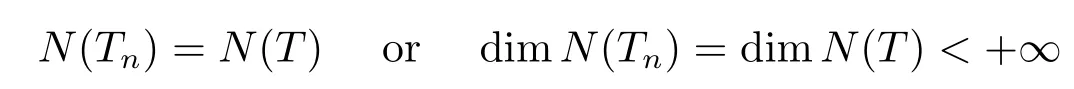
holds，then for all sufficiently large n，Tnis core invertible and→T

In this case，