The Center Problems and Time-Reversibility with Respect to a Linear Involution

YANG Jing(杨静)，YANG Ming(杨鸣)，LU Zhengyi(陆征一)

(1.Chengdu Institute of Computer Application，Chinese Academy of Sciences，Chengdu 610041，China; 2.University of Chinese Academy of Sciences，Beijing 100049，China;3.School of Mathematical Sciences，Sichuan Normal University，Chengdu 610068，China)

Abstract: In this paper，the relationship between time-reversibility and the center of a planar quadratic polynomial system in R2 is considered.The necessary and sufficient conditions for the system to be time-reversible w.r.t.a linear involution are obtained.These conditions guarantee that the system has a center at the origin which is symmetric w.r.t.a straight line.

Key words: Polynomial differential system; Time-reversibility; Linear involution; Center

1.Introduction

In the qualitative theory of differential systems，of particular significance are the existence and the number of limit cycles from famous Hilbert 16th problems.In order to know how many limit cycles can bifurcate，it is necessary to have an in-depth understanding of the conditions under which the singular point is a center.If an analytic differential system has a non-degenerate center at the origin，then after making a linear transformation of the variables and rescaling the time variable，it can be transformed into the form as follows:

where P(x，y) and Q(x，y) are analytic functions without constant term.For the purpose of obtaining the necessary and sufficient conditions for the system (1.1) to have a center，the first step is to obtain the necessary conditions by computing the first several focal values and then to prove the sufficiency of these conditions.The construction of integrating factors[14]and the verification of Poincar´e symmetric principle[10]which has been presented in 1892 are two major methods of checking the sufficiency.Actually，a system satisfying the Poincar´e principle is a time-reversible one w.r.t.a special linear map such that the system has an axisymmetric center.

The time-reversible theory of differential systems emerged in 1915 with Birkhoff’s work on three bodies[1].In 1976，Devaney[6]developed the theory of reversibility such that the study of it is expanded to analytic differential systems.For planar analytic differential systems，a reversible center has always received attention[11].Gin´e and Maza[7]obtained some results about degenerate center and time-reversibility.In 2018，by using the time-reversibility w.r.t.a special linear map，Boros et al.[2]obtained some new sufficient conditions for Lotka reactions with generalized mass-action kinetics to have a center.Recently，HAN et al.[8]considered a general polynomial quadratic system without constant term in R2and obtained some algebraic conditions for the system to be time-reversible one w.r.t.a linear involution.In their computational procedure，the Closure Theorem[5]which just holds over an algebraically closed field has been misused.

The purpose of the present paper is to give the necessary and sufficient conditions for the following quadratic system to be time-reversible w.r.t.a linear involution.

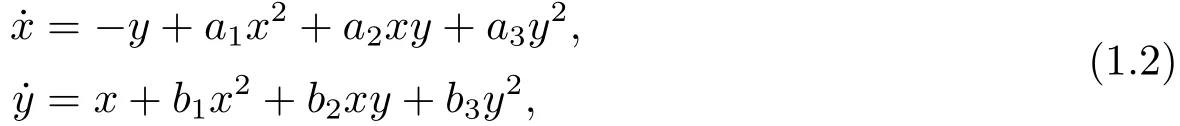
where (x，y)∈R2，ai，bi∈R (i=1，2，3).This kind of problems can be converted into ones of obtaining the set of zero roots of some polynomials with parameters.The concept of triangular decomposition emerges in a lot of computer algebra methods for computing the roots of polynomial systems.For example，the characteristic set of Ritt-Wu’s method[15-16]，Groebner bases[3]，resultant[5]and so on.The regular chain which was introduced by Kalkbrener[9]and YANG and ZHANG[13]independently is also a kind of triangular decompositions and well-developed in complex field.In 2013，CHEN et al.[4]considered the real solutions for semi-algebraic systems and proposed the following Lemma.

Lemma 1.1[4]Let S be a semi-algebraic system of Q[x].Then one can compute a triangular decomposition of S，that is finitely many regular semi-algebraic systems Bisuch thatwhere ZRdenotes the zero set in Rnof a semi-algebraic system.

In this paper，by using the regular chain theory[4]，the necessary and sufficient conditions for the system (1.2) to be time-reversible w.r.t.a linear involution are obtained in Section 2.In Section 3，we show that these conditions can ensure the system to have a center by using the result of Teixeire and YANG[12]which indicates that the system (1.1) is time-reversible if and only if it is a center.

2.Time-Reversible with Respect to a Linear Map

Firstly，we introduce the definition of a time-reversible system.

Definition 2.1[12]A Crplanar differential system (r ∈N ∪{∞，ω})，

having a singularity at the origin is time-reversible if there exists a diffeomorphism φ:R2→R2satisfying φ ◦φ=Id such that

where X is the vector field associated to the system (2.1)，and φ*represents the tangent map of φ，i.e.，φ*X = D(x，y)φ(x，y)X in the local coordinates.The map φ is called an involution.Fix(φ)={(x，y)∈R2|φ(x，y)=(x，y)} is called fixed point set of φ.

Let

where λi，δi∈R (i = 1，2)，According to Definition 2.1，when φ ◦φ = Id，φ is an involution.Hence，we have

Clearly，(2.3) is equivalent to

or

Note that condition (2.4) corresponds to two trivial situations: φ(x，y) = ±(x，y).From the definition，the following is a direct result.

Lemma 2.1A linear map φ(x，y)=(λ1x+λ2y，δ1x+δ2y)is an involution if and only if one of the following conditions is satisfied:

1) λ2=δ1=0，λ1=δ2=±1，

2) λ1=-δ2，+λ2δ1=1，

where λi，δi∈R (i=1，2).

It is clear that the fixed point set of a linear map satisfying the condition 1) of Lemma 2.1 is either the origin or the whole space.If a linear map satisfies the condition 2)of Lemma 2.1，the fixed point set is

This set is a straight line passing through the origin.

Let

From Definition 2.1 and Lemma 2.1，we have

Lemma 2.2The system (1.2) is time-reversible w.r.t.a linear map φ(x，y) = (λ1x+λ2y，δ1x+δ2y) if and only if the map φ is an involution such that

In the case where the linear map φ satisfies the condition 1) of Lemma 2.1，the map φ is an involution satisfying φ(x，y) = (x，y) or φ(x，y) = -(x，y).Furthermore，the equality(2.6) in Lemma 2.2 is equivalent to P(x，y) = Q(x，y) = 0.Hence，the system (1.2) is not time-reversible w.r.t.these involutions.

Now we consider the case where the linear map φ satisfies the condition 2) of Lemma 2.1.Since the fixed point set of the linear map，in this case，is a straight line，then the phase diagram of the system (1.2) is symmetric w.r.t.a straight line if the system is time-reversible w.r.t.a linear map.The linear part of (2.6) of Lemma 2.2 is as follows，

therefore，we have the following Lemma.

Lemma 2.3The system (1.2) is time-reversible w.r.t.a linear map φ(x，y) = (λ1x+λ2y，δ1x+δ2y) if and only if the following conditions are satisfied:

where (x，y)∈(0，R2)，λiand δi∈R，i=1，2.

According to Lemma 2.3，we just need to consider the involution in the form of φ(x，y)=(λ1x+λ2y，λ2x-λ1y).Let

then H(x，y)=0 holds for all value of (x，y) in (0，R2).Let

By Lemma 2.3，the necessary and sufficient conditions for the system (1.2) to be timereversible w.r.t.a linear map is equivalent to the necessary and sufficient conditions of the polynomial set Cof to have a real root in variables λ1and λ2.

The following is the main result of the present paper which gives a complete description of a time-reversibility w.r.t.a linear involution.

Theorem 2.1The system (1.2) is time-reversible w.r.t.a linear map if and only if one of the following conditions is satisfied:

Here

ω4=(a2a3+b3b2)/(a2b2+4a3b3)，

ω5=a23+3 a22b3-a2b22-b22b3-4 b33，

ω3=(a3-b2)a23-3 a22b2b3+(4 a33+(-3 b22-12 b32)a3+b23)a2+16 b3(a33-3/4 a32b2-a3b32+1/16 b23+1/4 b2b32)，

ω2= (a2-2 b1-b3)a13+3 a3(a2-b1)a12+((3 a2+3 b3)a32-(b1+b3)2(a2-b3))a1+a3((a2+b1+2 b3)a32-(b1+b3)2(a2+b1))，

ω1= (a2-2 b1+2 b3)a13+((3 a2-6 b1+6 b3)a3-3 b2(b1+b3))a12+((3 a2-6 b1+6 b3)a32-6 b2(b1+b3)a3+(b1+b3)2(a2+2 b1-2 b3))a1+(a2-2 b1+2 b3)a33-3 b2(b1+b3)a32+(b1+b3)2(a2+2 b1-2 b3)a3+b2(b1+b3)3.

The Proof of Theorem 2.1The crucial step of proving Theorem 2.1 is to obtain the necessary and sufficient conditions for the existence of the real roots of polynomial set Cof.The set Cof corresponding to the system (1.2) consists of seven polynomials:

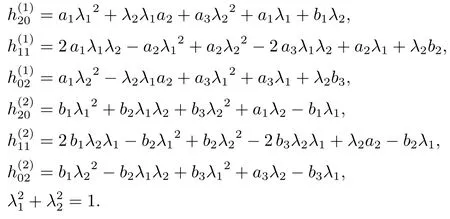
By using the command in the computer algebra system Maple，i.e.，

RegularChains:-RealTriangularize，

we obtain a triangular decomposition of these polynomials.In the order of b2＞a2＞b3＞b1＞a3＞a1＞λ2＞λ1，the triangular decomposition has six regular semi-algebraic systems such that the union of their real root sets is exactly the real root set of Cof.

Conditions (A1)，(A2)，(A3)，(A10) in Theorem 2.1 can be obtained directly from the regular semi-algebraic systems Ti，i=2，...，6 as follows

The other conditions can be obtained by analysing the necessary and sufficient conditions of the regular semi-algebraic system T1to have real roots in variables λ1，λ2.The system T1is as follows:

1) When a1-a3，by the equalities (2.10) and (2.11)，we have

By substituting λ1，λ2into (2.12) and (2.13)，we have

Inequalities in (2.14) lead to b1+b30，(a1+a3)2(b1+b3)2and 3(a1+a3)2(b1+b3)2.Hence，ω1=ω2=0.Condition (A9) in Theorem 2.1 is proved.

2) When a1=-a3，equality (2.11) leads to

Inequalities-1 ＜λ1＜1 together with equality=1 lead to λ20.Hence，b1+b2=0.By substituting a1=-a3and b1=-b3into T1，we have

(i) When a1=-a3，b1=-b3and a2λ1-b30，we can rewrite the equality (2.21) as

Substituting λ2into equality (2.22)，we obtain

Since the inequalities in(2.14)lead to(λ1+1)(2 λ1-1)0，the equality(2.25)is equivalent to

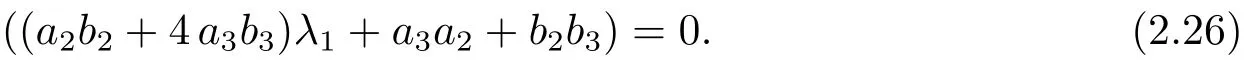
(a) When a2b2+4 a3b30，by the equality (2.26)，we have

The inequalities in (2.14) lead to 0 ＜|ω4|＜1，a2a3+b3b20，(2a3-b2)(a2-2b3)0.By the equality (2.27)，we have

Therefore，a2λ1-b30 is equivalent to a30 and a2±2b3.Furthermore，(2a3-b2)(a2-2b3)0 is equivalent to 2a3-b20.Substituting λ1and λ2into the equality (2.20) leads to ω3=0.Therefore，the condition (A11) in Theorem 2.1 is proved.

(b) When a2b2+4 a3b3=0，the equality (2.26) is simplified to

Using the command

RegularChains:-RealTriangularize，

we can solve the polynomial equations

and obtain

When a1=-a3，b1=-b3，a2λ1-b30，a2=-2b3and b2=2a3，T1is simplified to the following form.

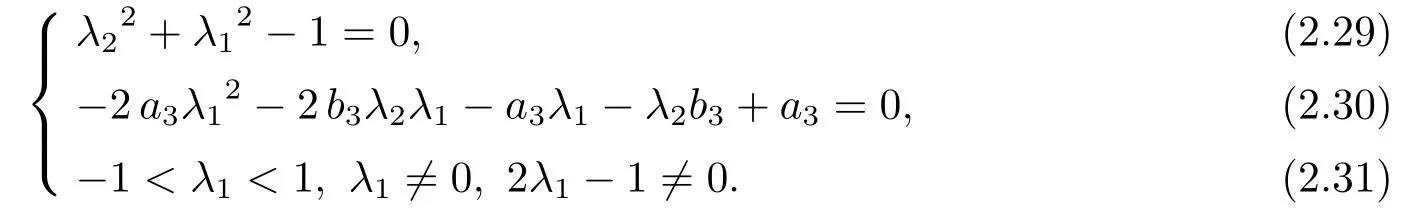
Since a2= -2b3，a2λ1-b30 is equivalent to b30 as well as 2λ1+10，the equality(2.30) leads to

By substituting λ2into the equality (2.29)，we have

where Δ(λ1) =Since λ1-1，the equality (2.33)is equivalent to Δ(λ1) = 0.According to the inequalities in (2.14)，λ1dose not belong toThus，Δ(-1) = -0，Δ(1) =0，Δ(0) = (a3+b3)(a3-b3)0 and0 lead to a30，b30 and a3±b3.Furthermore，since Δ(-1)=-＜0 and Δ(1)=＞0，then Δ(λ1)=0 has real roots in the interval (-1，1).If λ1=then=2a30 contradicts Δ(λ1)=0.Hence a30 implies 2λ1+10.Condition (A6)of Theorem 2.1 is proved.

When a1=-a3，b1=-b3，a2λ1-b30，a2=2b3and b2=-2a3，T1takes the form

Because a2=2b3anda2λ1-b30 is equivalent to b30.And since λ1/by the equalities (2.34) and (2.35)，we have

Inequalities in (2.14) lead to a30，andHence，the condition (A8) of Theorem 2.1 is proved.

When a1=-a3，b1=-b3，a2λ1-b30，a3=0 and b2=0，T1becomes

λ20 and a2λ1-b30 lead to (a2λ1-b3)λ20，which contradicts the equality (2.40).

That a1=-a3，b1=-b3，a2λ1-b30，a2=0 and b3=0 leads to a contradiction.

(ii) When a1=-a3，b1=-b3，a2λ1-b3=0 and a20，we have

In this case，T1is simplified to

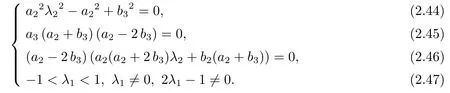
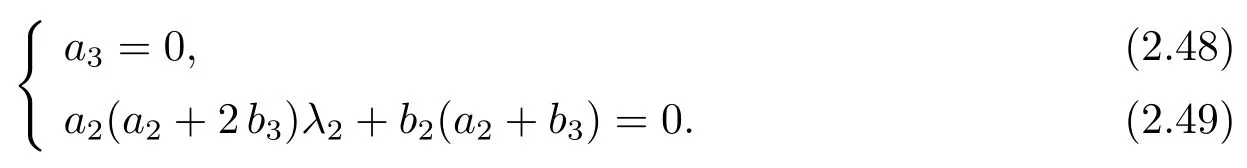
(a) When a1=-a3=0，b1=-b3，a2λ1-b3=0，a20 and a2+2 b30，we have

In this case，the equality (2.44) becomes

Since a2+b30，we have ω5= 0.Inequalities in (2.14) lead to -1 ＜＜1，b30 and a22b3.Condition (A7) of Theorem 2.1 is proved.

(b) When a1=-a3=0，b1=-b3，a2λ1-b3=0，a20 and a2+2 b3=0，the equality(2.49) is equivalent to b2= 0 because of a2+b30.Hence，by the equalities (2.43) and(2.44)，we have

Condition (A5) of Theorem 2.1 is proved.

(iii) When a1=-a3，b1=-b3，a2λ1-b3=0 and a2=0，T1is

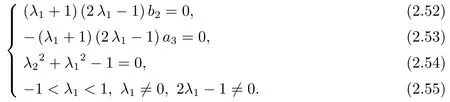
Hence b2=a3=0.Condition (A4) of Theorem 2.1 is proved.

The proof of Theorem 2.1 is complete.

3.Center and Phase Diagram

Lemma 3.1[12]Consider the Crdifferential system (r ∈N ∪{ω})，

where f(x，y) = o(|x2+y2|)，g(x，y) = o(|x2+y2|)，(R2，0) is a neighborhood of the origin.The system (3.1) is time-reversible if and only if the origin is a center.

By Lemma 3.1 and according to the relationship between a linear involution and its fixed point sets in Section 2，we have

Fig.3.1 Phase diagram

Theorem 3.1If the system (1.2) satisfies one of the conditions of Theorem 2.1，the origin is a center.Furthermore，the phase diagram near the origin is symmetric w.r.t.a straight line.

Figure 3.1 is the phase diagram of the system (1.2)，if its parameters satisfy a1= b1=b2= -a3= -b3= 1/2，a2= 7/4 for the condition (A11) in Theorem 2.1.In this case，the system takes the form

which is time-reversible w.r.t.the involution

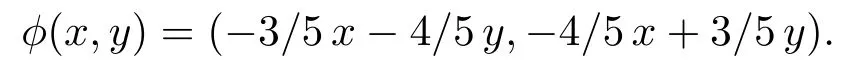
The fixed point set is {(x，y) | 2x+y = 0} represented by dotted line.The solid curves represent orbits nearing the origin.