具有随机保费和交易费用的最优投资-再保险策略

杨鹏，杜挺

(1.西京学院理学院，陕西 西安710123; 2.西安交通大学数学与统计学院，陕西 西安710049)

1.引言

最优投资-再保险策略选择问题，是金融数学的一个研究热点.该问题的研究框架是，保险公司通过再保险减少风险，通过投资增加财富，在最大化或最小化一些目标函数下，求得最优投资和再保险策略.文[1]应用随机控制理论研究了扩散风险模型的最优投资问题，获得了最优投资策略和值函数的显式解.文[2]研究了和文[1]类似的问题，区别在于考虑投资时假设含有多个风险资产并且考虑了再保险，文[2]也获得了最优投资和再保险策略以及值函数的显式解.最近，有很多学者研究了最优投资-再保险问题.文[3]研究了CEV模型下的最优投资-再保险问题;文[4]研究了保险市场和金融市场具有相依情形下的投资-再保险问题; 文[5]研究了最优投资超额损失投资-再保险问题; 文[6]研究了投资者只能获得部分信息下的最优投资-再保险问题.

在上述文献中，保险公司的保费收入都是常数，然而实际中保险公司的保费收入不一定是常数.比如在汽车保险中，保险公司制定下一年的保费通常依据上一年的理赔情况; 养老保险保费的缴费每年也都是动态变化的.因此，考虑随机保费才更符合实际.文[7]研究了随机保费风险模型，最近研究随机保费风险模型的文献越来越多.文[8]研究了随机保费风险模型的折现惩罚函数; 文[9]研究了收入和损失具有相依性下，随机保费风险模型的折现惩罚函数; 文[10]研究了随机保费风险模型的最优分红策略; 文[11]研究了随机保费风险模型的破产概率.

据我们所知，目前还没有学者研究随机保费风险模型的最优投资-再保险策略选择问题，因此本文对该问题进行了研究.考虑再保险时，大部分学者都是按期望值原理计算再保险保费.但是，期望值原理计算再保险保费，只考虑到了理赔的期望没考虑理赔的方差.基于对期望值原理的改进，本文按照方差原理计算再保险保费.保险公司在投资时，买卖股票是需要佣金、印花税、过户费的，即买卖股票是有交易费用的，尤其是频繁交易时，交易费用是很大的.因此在风险资产上投资时，应考虑交易费用，考虑交易费用才更符合实际情况.然而，在最优投资-再保险问题中，考虑交易费用的文献还非常少.具我们所知，只有文[12]对扩散风险模型，考虑了含交易费用的最优投资-再保险问题.本文对文[12]的模型进行推广，研究了随机保费收入下，跳-扩散风险模型带交易费用的最优投资-再保险问题.

2.模型和Hamilton-Jacobi-Bellman(HJB)方程

在现实中受一些不确定因素和保险公司推出的一些激励措施的影响，保险公司的保费收入一般具有随机性，因此考虑随机保费收入更符合实际.文[7]在Cram´er-Lundberg保险模型中引入了随机保费，本文把文[7]的模型推广到跳-扩散风险模型，即考虑如下带随机保费的跳-扩散风险模型

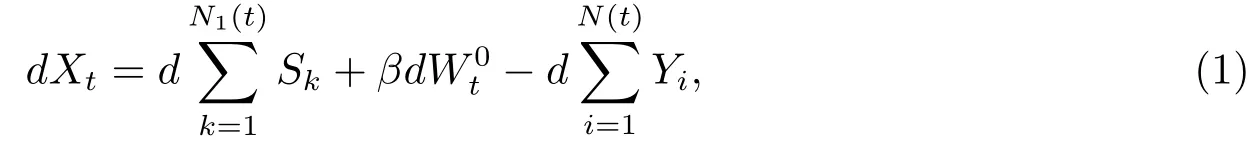
其中{N1(t)，t ≥0}是参数为λ1＞0的泊松过程，表示到时刻t为止收到的保费次数; {Sk，k =1，2，···}是一列独立同分布的(严格)取正值的随机变量，Sk表示第k次保费收入额，其通常的随机变量记为S，共同分布为G(s)，密度函数为是到时刻t为止收到的总的保费; {Yi，i=1，2，···}是一列独立同分布的(严格)取正值的随机变量，其通常的随机变量记为Y，共同分布为F(y)，密度函数为f(y)，F(0) = 0，Yi表示第i次赔付的大小; {N(t)，t ≥0}是参数为λ ＞0的泊松过程，表示到时刻t为止总的索赔发生次数; {，t ≥0}是标准布朗运动，表示不确定的收益或损失，β ≥0是常数.此外，假设{Yi，i = 1，2，···}，{N(t)，t ≥0}，{N1(t)，t ≥0}，{Sk，k =1，2，···}和{，t ≥0}是相互独立的.{Xt，t ≥0}为保险公司在t时刻的盈余.

再保险是保险公司分散风险的主要方式，因此我们下面考虑再保险.本文考虑的再保险方式是比例再保险，保险公司再保险的比例为(1-a(t))，a(t)为保险公司的自留比例，0 ≤a(t)≤1.也就是说在每次发生理赔时，保险公司支付100a(t)%，同时再保险公司支付剩余的100(1-a(t))%.再保险公司为保险公司分担一部分理赔，保险公司则需要向再保险公司支付一定的保费，再保险保费按照方差原理计算，即(1-a(t))λµ1+α(1-a(t))2λµ2，其中α ＞0为一常数，µ1=E(Y)，µ2=E(Y2).考虑比例再保险后，保险公司在t时刻的盈余变为

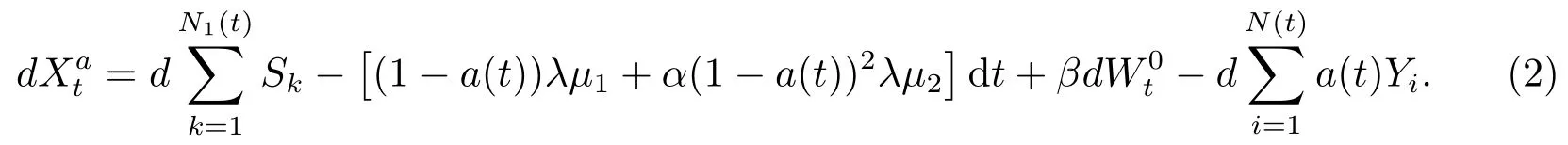
在金融市场上投资是保险公司增加财富的主要方式.本文考虑的金融市场由n+1个金融资产组成，其中一个是无风险资产(如: 债券)，时刻t的价格为{B(t)，t ≥0}满足方程dB(t) =r0B(t)dt，这里r0＞0为无风险利率.n个风险资产(如:股票)，在时刻t时的价格为{Si(t)，t ≥0}，i=1，2，··· ，n，它们满足下面的随机微分方程

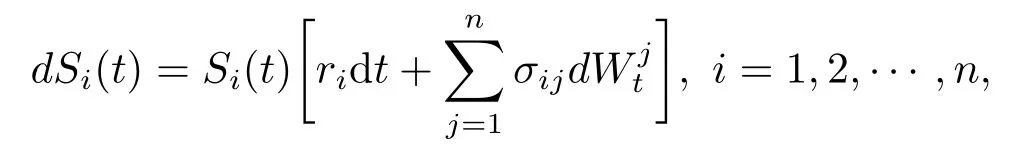
其中ri≥ r0，σij＞ 0为常数，是n维布朗运动，假设j =0，1，2，··· ，n相互独立.{Ft，t ≥0} 是，j =0，1，2，··· ，n生成的自然流.

为了使投资问题求解方便，很多文献在考虑投资时都没有考虑交易费用.然而在现实中，投资经常存在交易费用.因此，本文买卖风险资产时考虑交易费用，设θb(t) =[θb1(t)，θb2(t)，··· ，θbn(t)]′和θs(t) = [θs1(t)，θs2(t)，··· ，θsn(t)]′分别为买和卖风险资产的交易费用，即买一个单位的风险资产i将花费(1+θbi(t))Si(t)的费用，卖一个单位的风险资产i将得到(1 - θsi(t))Si(t)的收益.设πb(t)，πs(t)分别为买和卖风险资产的资金，这里πb(t) =所以在风险资产上的投资额为πb(t)-πs(t).因为不能同时买卖风险资产，所以有=0.本文我们禁止卖空(no-shorting)，即要求≥0，i = 1，2，··· ，n.若某个＜0)，则表示投资者以利率r0从银行贷款，来对冲的部分.

我们选取再保险时保险公司的自留比例a(t)和保险公司在风险资产上的投资额πb(t)，πs(t)作为控制变量.为了书写简洁，记πb:=πb(t)，πs:=πs(t)，a:=a(t)，以及π :=(a，πb，πs).一旦π被选定了，则保险公司的财富过程变为

其中I是n维单位列向量，r =(r1，r2，··· ，rn)′，D =(σij)n×n，A′为A的转置.

定义2.1一个策略π称为可行的，如果π关于流{Ft，t ≥0}是可料的，且对于t ≥0，过程π满足下面三个条件: 1) 几乎处处有几乎处处有∞; (3) 0 ≤a(t)≤1.所有可行的策略记为Π.

假设保险公司的目的是，寻找最优再保险和投资策略使投资终止时刻T时财富的期望效用最大.设效用函数为这里δ ＞0，γ ＞0.显然有u′＞0，u′′＜0.记Vπ(t，x)为时刻t，盈余为x，策略为π时，终止财富的期望效用，即目标是寻找最优的值函数

和最优的策略π*使得

类似于文[13]，可得下面的HJB方程和检验定理.定理的证明参考文[13]，本文不再证明.

定理2.1假设由(4)定义的值函数V(t，x)关于t是连续可微，关于x是二次连续可微的函数，则V(t，x)满足下面的HJB方程

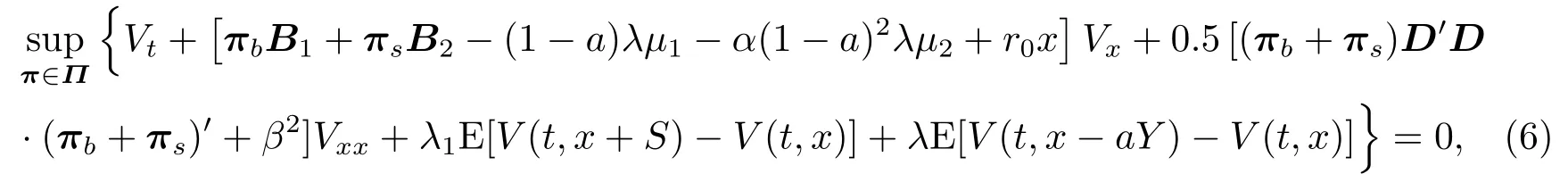
边界条件

这里Vt，Vx，Vxx分别为V(t，x)关于t的一阶导数，关于x的一阶导数和关于x的二阶导数，且B1= (r1- r0- θb1，r2- r0- θb2，··· ，rn- r0- θbn)′，B2= (r1+ r0- θs1，r2+ r0-θs2，··· ，rn+r0-θsn)′.

定理2.2(检验定理) 设W(t，x) ∈C2是一凹函数，为HJB方程(6)的解，满足边界条件(7)，则W(t，x)恰好等于最优值函数V(t，x).进一步，若π*使得

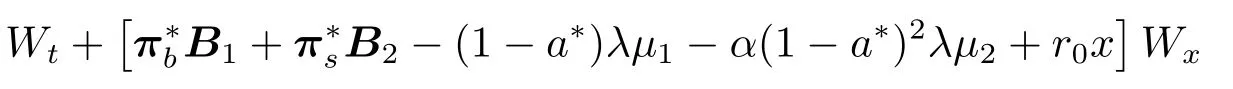
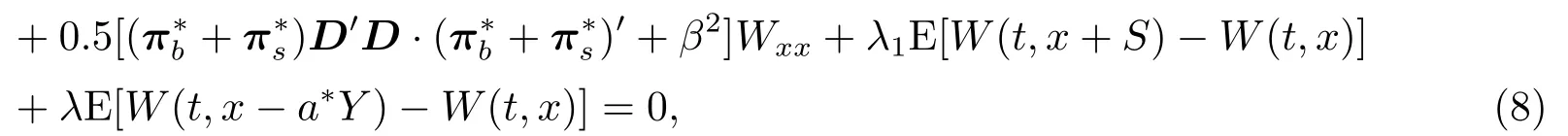
则π*是最优的策略，也就是W(t，x)=V(t，x)=Vπ*(t，x).

3.最优投资和再保险策略

为了得到最优的投资和再保险策略，首先给出下面的定理3.1.

定理3.1下面关于a的方程

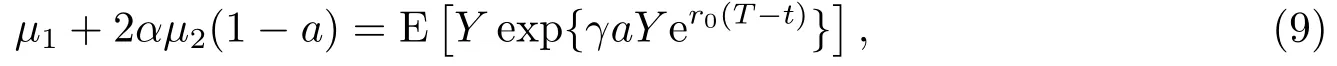
证设

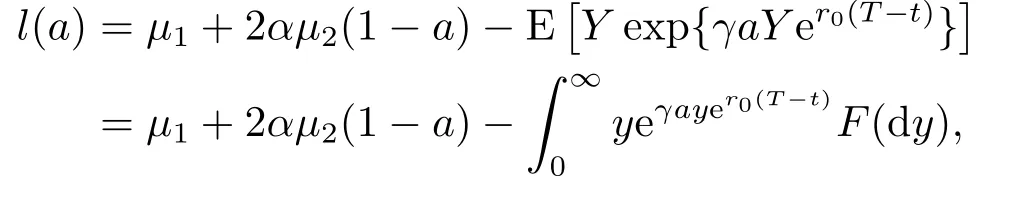
则

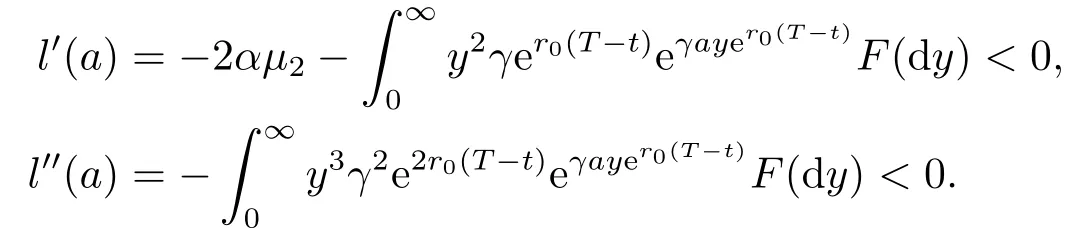
因此，l(a)是关于a单调递减的凹函数.又因为

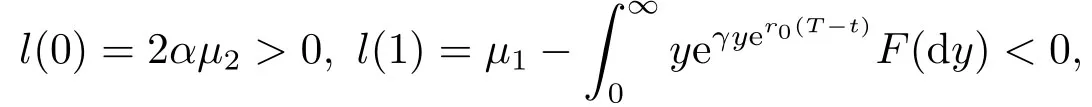
下面给出本文的主要结果.

目前我国反腐败法律制度党内立法多、国家立法少，党内制度又往往不能及时转化为国家法律法规，因而其强制性和约束力偏弱。理顺二者的关系:一是要处理好宪法与的党内反腐法规关系;二是要处理好国家反腐立法与党内反腐立法的互动关系;三是要处理好党内反腐法规与国家法律有关反腐规定的互补关系;四是要严格区分党内反腐立法和国家反腐立法的权限;五是要构建党内立法与国家立法的衔接机制;六是要适时把成熟的党内法规上升为国家法律;七是要加强党内执法和国家执法过程中的联系与沟通;八是要建立党内违章审查制度。

定理3.2对于财富过程(3)，最优比例再保险策略a*为下述方程的根

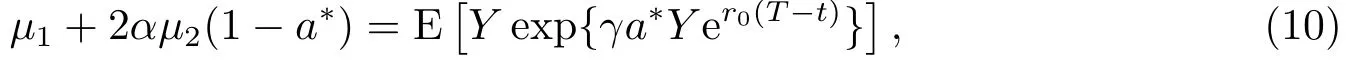
最优投资策略为

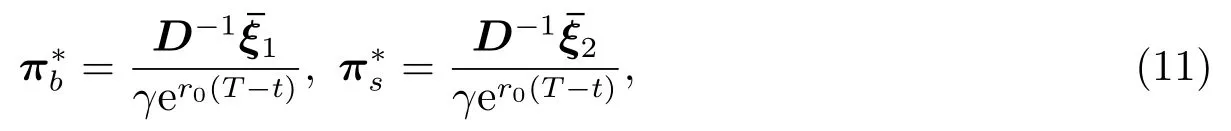
最优的值函数为

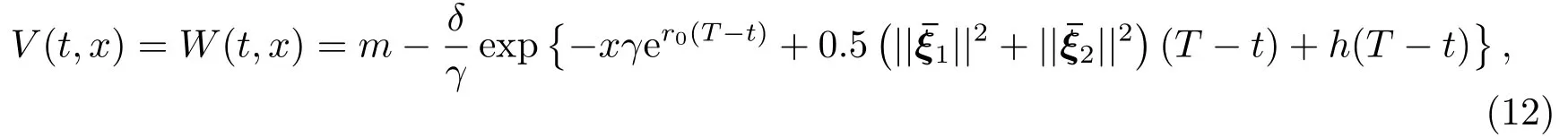
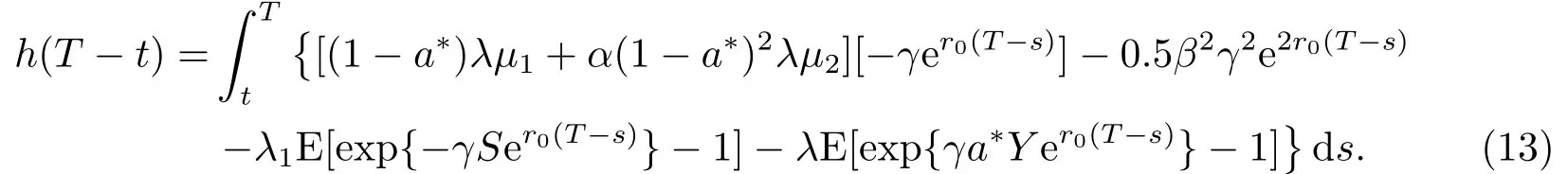
证设W(t，x) ∈C2是一凹函数，为HJB方程(6)的解，满足边界条件(7).由文[12]中的引理1-4，我们有

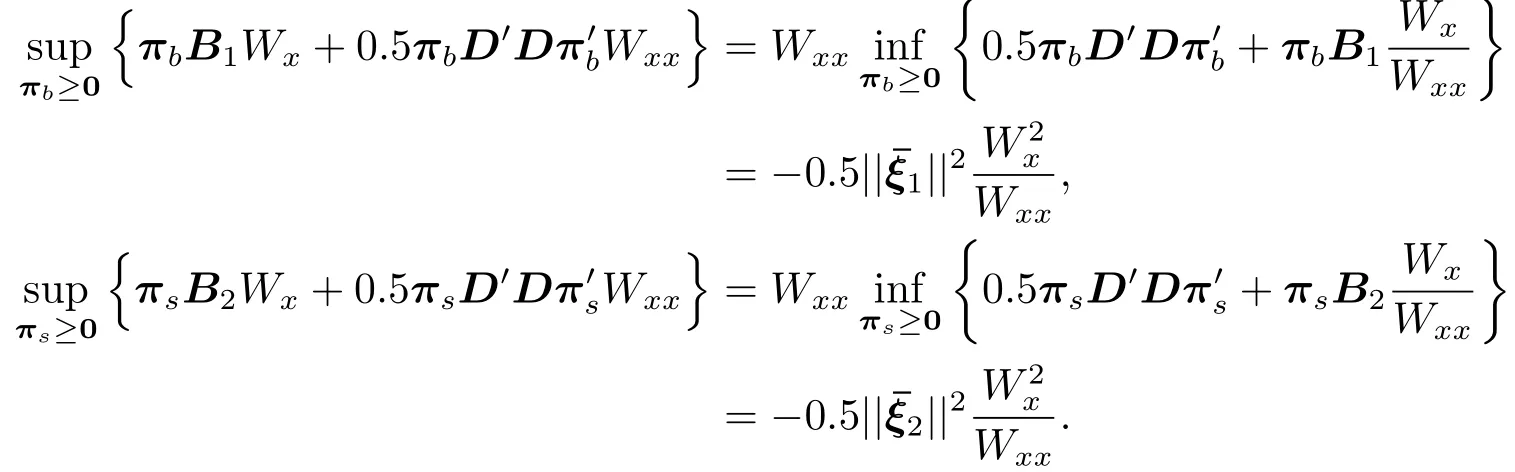
与文[12]类似的，最优投资策略满足下式

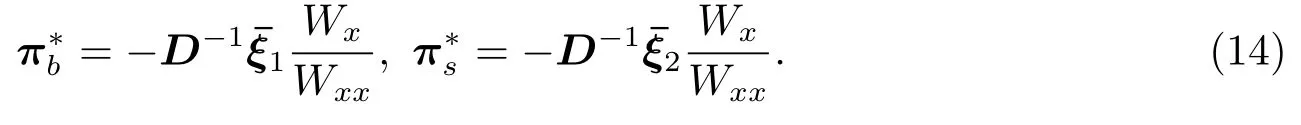
把(14)式代入(6)式，得到

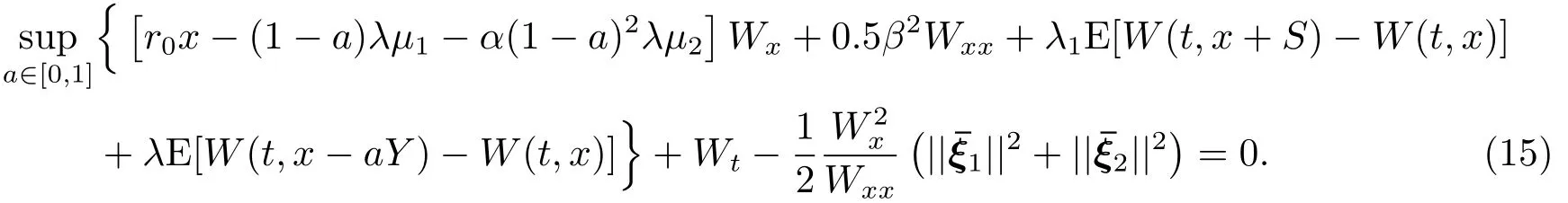
和文[1]类似的，假设W(t，x)满足如下形式

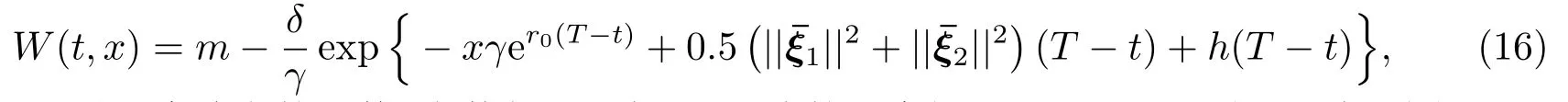
这里h(·)是一个确定的函数，它使得(16)式是(15)式的一个解，且h(0)=0.从(16)式，我们可以得到

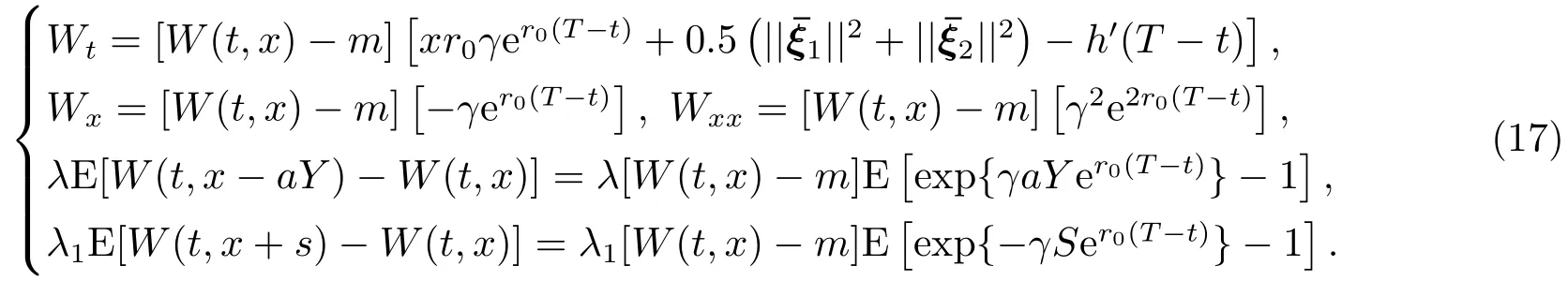
把(16)式和(17)式代入(15)式，有

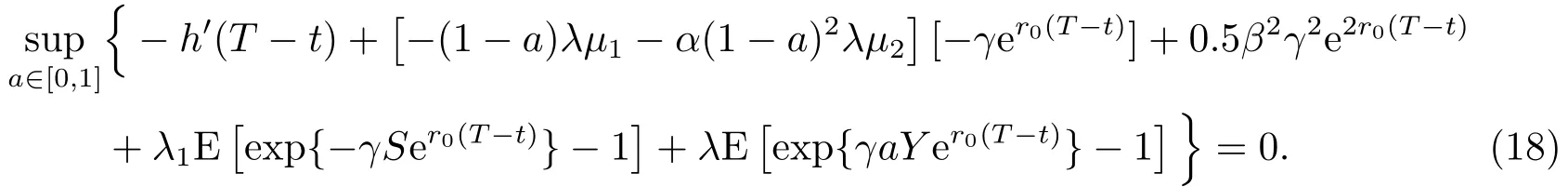
设

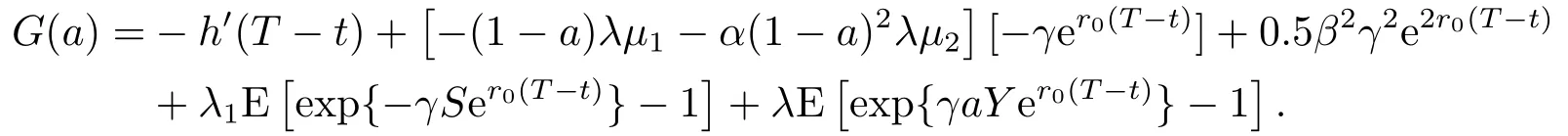
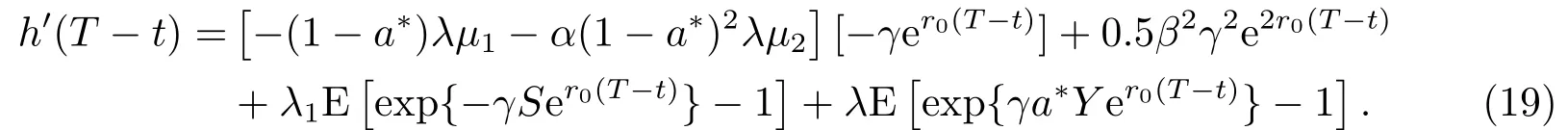
(19)式两端从t到T求积分可得h(T -t)满足(13)式.h(T -t)代入(16)式，由定理2.2，得值函数V(t，x) = W(t，x)，且满足(12)式.W(t，x)代入(14)式，得到最优投资策略满足(11)式.证毕.

4.数值计算及经济分析

本节通过数值计算，解释模型参数对最优策略的影响，并进一步给出结果的经济意义.

设保费收入和理赔额的分布都服从参数为1的指数分布，即G(s) = 1 - e-s，s ＞0，F(y)=1-e-y，y ＞0.根据方程(9)，我们得到最优比例再保险策略a*满足下面的方程

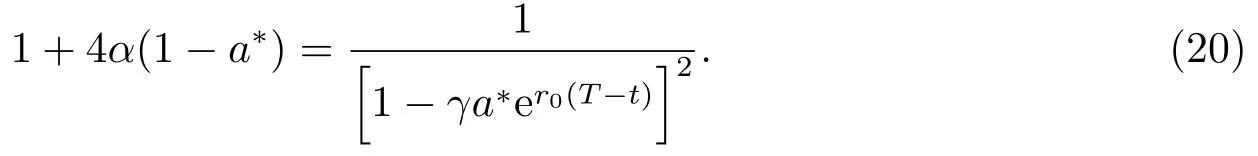
例1设r0= 0.05，T = 5，t = 1，γ = 0.5，则由(20)式可得α对最优再保险策略a*(t)的影响，结果见图1.从图1中可以看出，a*(t)关于α是单调递增的.α越大，说明再保险的保费越高;因此，随着α增加，保险公司将减少再保险的比例，即保险公司自留比例增大.

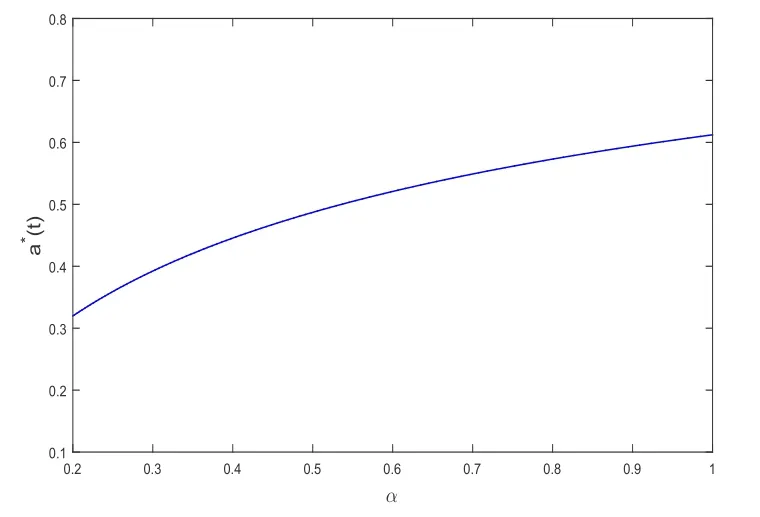
图1 α对a*(t)的影响

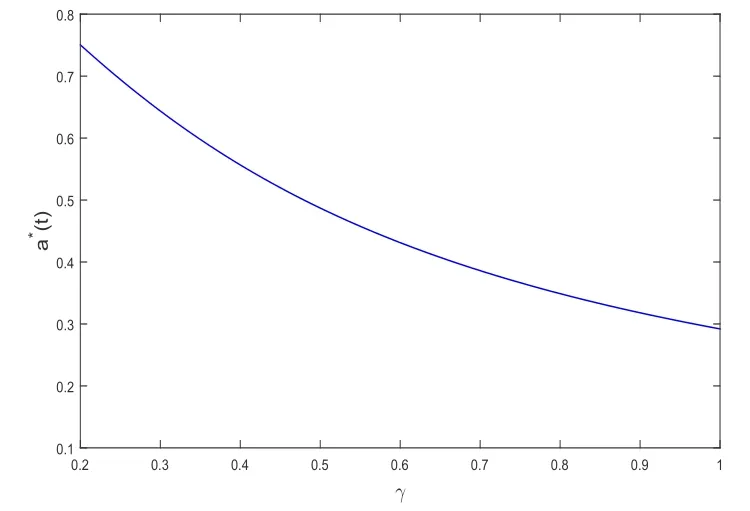
图2 γ对a*(t)的影响

例2设r0= 0.05，T = 5，t = 1，α = 0.5，则由(20)式可得γ对最优再保险策略a*(t)的影响，结果见图2.从图2可以看出，a*(t) 关于γ是单调递减的.γ 是绝对风险厌恶参数，γ越大，保险公司所承受的风险越大.因此，当γ增大时，保险公司更希望通过再保险转移理赔风险，即保险公司自留比例减少.

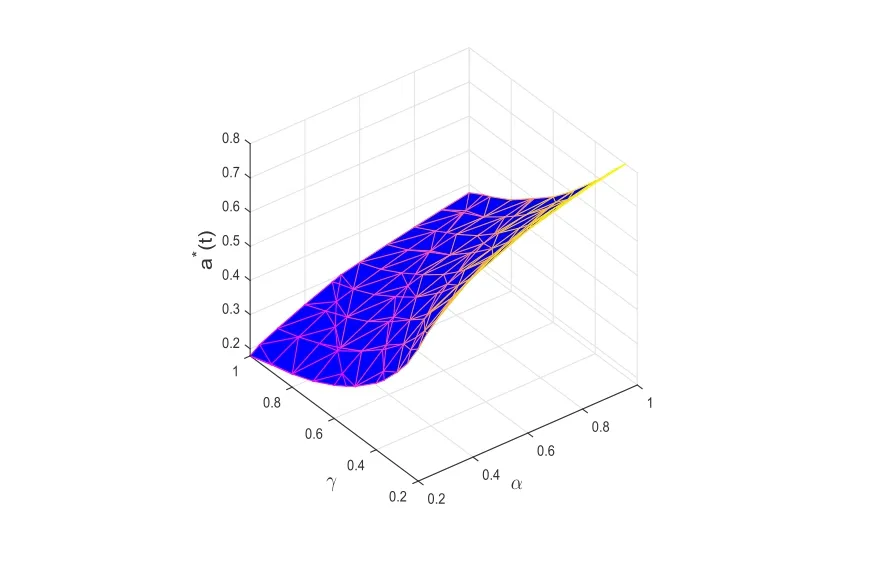
图3 α和γ对a*(t)的联合影响

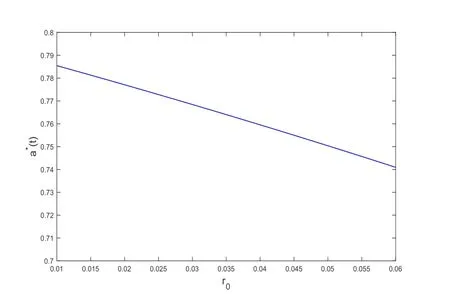
图4 r0对a*(t)的影响

例3设r0= 0.05，T = 5，t = 1，图3进一步解释了α和γ对最优再保险策略的联合影响.从图3可以看到，相对α来说，γ 对最优再保险策略的影响更大.这说明，当再保险公司增加保费时，如果保险公司面临的不确定因素增大，保险公司更愿意寻求再保险公司抵御理赔风险.

例4设T = 5，t = 1，α = 0.5，γ = 0.2，则由(20)式可得r0对最优再保险策略a*(t)的影响，结果见图4.从图4可以看出，a*(t)是r0的减函数.r0是无风险利率，r0越大，保险公司从无风险资产的期望收益越大.收益增大了保险更不愿意承担风险，因此更希望寻求再保险公司来抵御理赔风险.