带有N策略的不可靠重试队列的均衡策略分析
2021-01-07唐韵刘力维
唐韵,刘力维
(南京理工大学理学院,江苏 南京210094)
1.引言
重试排队系统在我们的日常生活中无处不在,并且学者对它的研究已经非常广泛,但大部分都是利用随机过程或动态规划技术进行系统性能分析,而较少从经济学角度进行研究.文[1]对已有的重试排队系统的研究方法和成果进行了总结.文[2]利用嵌入马尔科夫链和母函数的方法研究了一种批到达重试排队系统,求得了重试轨道中队长的分布,进而得到各性能指标.文[3]研究了带有恒定重试率的单服务台排队系统的顾客最优策略和最大社会收益.文[4]针对不可见情形和可见情形的经典单服务台重试排队系统,研究了顾客均衡策略和社会最优的止步策略.文[5]针对局域网的应用研究了带有恒定重试率和延迟休假的M/M/1排队系统,得到了顾客进入系统的纳什均衡策略和社会价格最优策略.文[6]研究了带有恒定重试率和N策略的M/M/1 排队系统,分析了顾客行为和社会收益最大问题.文[7]在文[6] 的基础上研究了带有启动时间的情形.文[8]研究了带有恒定重试率和工作假期的单服务台排队系统,分析了顾客均衡策略和社会最优策略.
因为系统高昂的建设成本和运行成本,现实生活中的很多服务系统会采用某些策略来控制系统的启动和关闭,其中N策略应用得十分广泛.文[9]第一次在M/M/1系统中提到了N策略的概念.之后,文[10-12]用了几种不同的方法研究了这种控制策略.值得注意的是N策略虽然在经典排队系统中已经被研究,但是从经济学角度来研究它的文献还比较少.文[13]针对不可见情形和可见情形,研究了带有N 策略和假期的排队系统的顾客均衡策略和社会最优策略.文[14]将文[13] 拓展为带有异类顾客的情形.文[15]针对部分可见情形,研究了假期排队系统的顾客策略行为和社会最优问题.
另外,在许多排队模型中会假设服务台完全可靠,但很明显这种假设是不符合实际的,因为服务台在服务顾客时可能会发生损坏且需要立即维修的情况无法被忽视,这就是带有不可靠服务台的排队系统.带有不可靠服务台的排队模型可以应用于计算机通信系统和机械生产制造系统中,机器可能因工作时间过长或某些自身原因发生故障,则不得不停止服务,直至维修结束才能继续进行服务.文[16]最早研究服务台可能发生故障的排队系统,并得到了相关数量指标.文[17]研究了M/G/1不可靠服务排队系统,并首次给出了该系统的可靠性分析.文[18]针对完全可见情形和几乎可见情形,研究了一个带有故障和维修期的M/M/1排队系统并得到顾客的均衡策略.文[19]在文[18]的基础上得出当队长信息不可见时顾客遵循混合均衡止步策略.文[20]又将以上结果推广到离散不可靠服务排队系统中,给出了顾客的个体最优均衡策略.文[21]研究了带有服务中断的认知无线电网络系统,在该系统中主级用户的出现会导致次级用户的服务中断.文[22]针对队长可见情形和不可见情形,研究了带有灾难到达的M/M/1排队系统的纳什均衡和社会最优止步策略.文[23]研究了不可靠Mn/G/1排队系统的最优加入策略,其中顾客的到达率依赖于系统中的顾客数.
本文主要研究: 带有N策略和不可靠服务台且拥有恒定重试率的M/M/1排队系统.现在重试排队系统在工业工程和商业管理上的应用非常广泛.例如呼叫中心的管理模式: 如果代理商在客户打进电话时有空,则将立即为来电服务,如果发现所有服务台都忙,则客户必须挂断电话,并在随机时间后重试.在现代服务系统中,呼叫中心可以在客户到达时给他提供一些系统信息,例如,预期的等待时间和服务台状态,客户可以根据可用的信息及其预期收益来决定是否加入系统.我们在此基础上还考虑了N策略和不可靠服务台的情况,使得该模型具有更广的应用领域和现实意义.
2.模型描述
我们考虑一个带有N策略和不可靠服务台且拥有恒定重试率的M/M/1排队系统.顾客到达排队系统为参数为λ的泊松过程.如果到达的顾客发现服务台处于空闲状态,则他会立即被服务,在服务台前面没有等待空间,如果到达的顾客发现服务台处于繁忙状态,则他可能会加入虚拟的重试轨道,实际上,这些轨道中的顾客可以被看作“等待顾客”,当服务台处于空闲状态时,服务台会根据FCFS规则从“等待名单”中选择顾客进行服务,“等待顾客”的重试时间间隔服从参数为θ的指数分布,但是如果在这个过程中有新的顾客到达系统,则“等待顾客”的重试将会被打断,服务台会对新到达的顾客进行服务.我们假设服务时间服从相互独立且参数为µ的指数分布.服务台在服务一名顾客时会因为它到达“寿命”极限而损坏,服务台的“寿命”服从参数为γ的指数分布.如果服务台发生损坏,则它会被立即送去维修,且正在被服务的顾客需要等待服务台被修好,然后完成他的剩余服务,维修时间服从参数为α的指数分布,另外,服务台在被修好以后和新的一样,我们假设服务台在损坏的时候,新到达的顾客不会选择加入系统(包括重试轨道).当服务台处于休眠状态时,它不会为顾客提供任何服务,直到重试轨道中的顾客数达到给定的阈值N(N ≥1),服务台被启动,其启动时间可忽略不计.当服务台被启动以后,它会为所有的顾客提供穷尽服务,在这之后,排队系统会变空,服务台会再次进入休眠状态.我们假设到达时间间隔、服务时间、重试时间间隔、服务台“寿命”和维修时间相互独立.
新顾客到达排队系统的瞬间会决定加入系统或者止步.每一位顾客在完成服务后会获得回报R,并且他们在系统中的逗留期间(包括排队等待和被服务期间)的单位费用为C.假设每位顾客都是风险中立的且想自己的收益最大化,如果服务后得到的回报比逗留期间的费用大,则顾客会选择加入系统,如果服务后得到的回报等于或小于逗留期间的费用,则顾客会选择止步.我们假设:

其中最后一项表示不可靠排队系统的广义服务时间(见文[17]),这能够保证到达的顾客发现服务台处于空闲状态会选择加入系统.我们进一步假设顾客一旦做出进入系统的决定则不能反悔,即不能中途选择退出; 如果顾客决定止步也不能再次返回系统.
对于所研究的排队系统,定义{I(t),N(t),t ≥0}表示在时刻t时系统的状态,其中I(t)表示服务台的状态(0 : 休眠,1 : 繁忙,2 : 空闲,3 : 损坏),N(t) 表示表示轨道中的顾客数.很明显,随机过程{I(t),N(t),t ≥0} 在状态空间{(0,i),0 ≤i ≤N -1;(1,j),j ≥0;(2,k),k ≥1,(3,n),n ≥0} 上为一个连续时间马尔科夫链.
在这篇文章中,主要研究几乎不可见的情形,即到达的顾客只知道服务台的状态.在这个规则下顾客到达瞬间选择加入系统的概率就依赖于服务台当前的状态I(t),我们假设当顾客在发现服务台状态为i时均以相同的策略以概率qi(i = 0,1,2,3)加入系统,即有效均衡到达率λi=λqi(i=0,1,2,3),这说明λi≤λ.
因为假设条件(2.1)的存在,则当顾客到达系统时发现服务台处于空闲状态,他肯定会选择加入系统,这意味着λ2=λ,又因为假设服务台在损坏时,到达的顾客不会加入系统(包括重试轨道),即λ3=0,所以,在这两种情况下,顾客的决策行为是确定的,不受其它顾客决策行为所影响的.因此,只需要研究当服务台状态处于I(t)=0,1时(0: 休眠,1: 繁忙),到达顾客的决策行为.本文中,通过I(t)=0,1时顾客的均衡到达率来研究顾客的决策行为.该排队系统稳态存在当且仅当(见文[3,24]):

其系统状态转移率如图2.1所示.
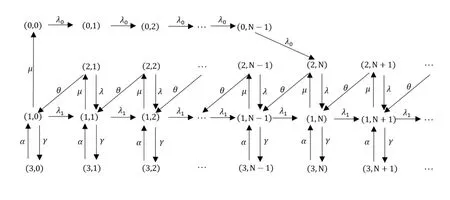
图2.1 系统状态转移率图
3.均衡到达率
在这一节里,我们研究在几乎不可见的情形下顾客的均衡到达率.令{p(0,i),0 ≤i ≤N-1;p(1,j),j ≥0;p(2,k),k ≥1;p(3,n),n ≥0}马尔科夫链{I(t),N(t),t ≥0}的稳态分布.则相应的母函数定义如下:

其中|z|≤1.我们得到如下初步结果.
引理3.1对于带有N策略和不可靠服务台且拥有恒定重试率的M/M/1 排队系统,若给定到达率(λ0,λ1,λ,0),则服务台状态i=0,1,2,3 的稳态概率分别如下:
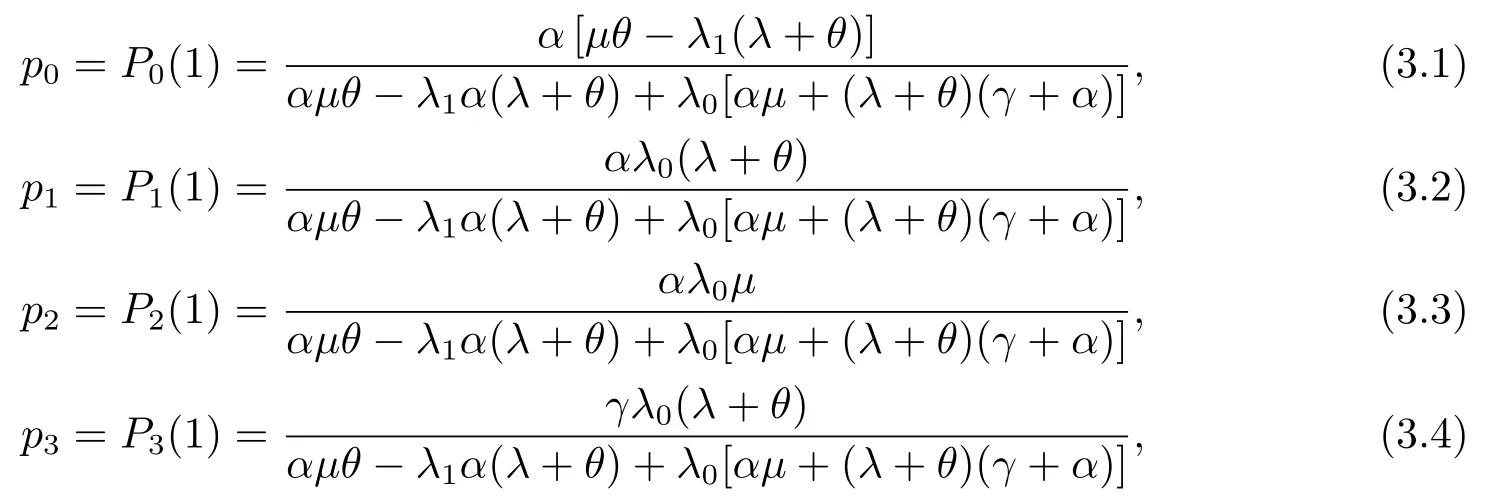
而且我们还可以得到如下等式:
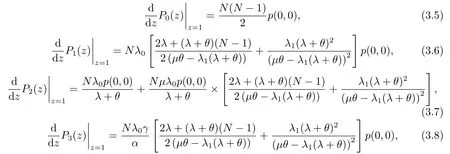
其中:

证稳态分布的平衡方程如下:

由(3.11)可以得到:
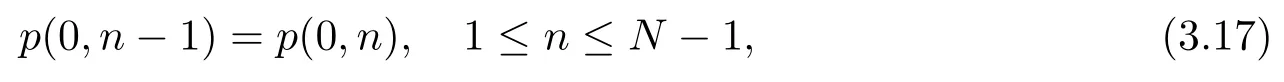
所以:

由(3.16)很容易可以得到:

由(3.12)和(3.13)可以得到:

将(3.19)带入上式可以得到:
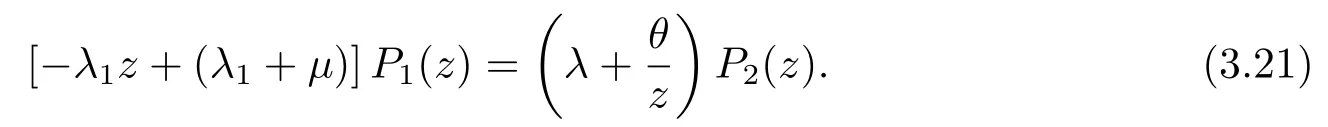
由(3.10)、(3.14)、(3.15)和(3.17)可以得到:
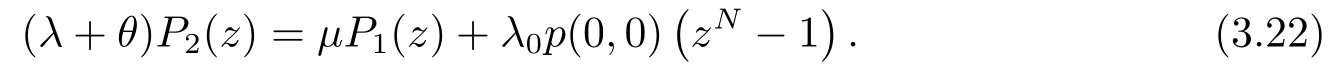
再联立(3.21)和(3.22)可以得到:
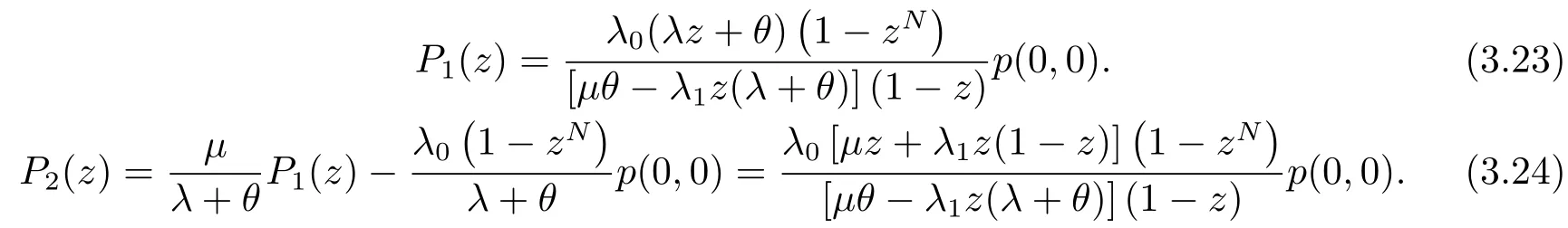
最后,由(3.19)可以得到:
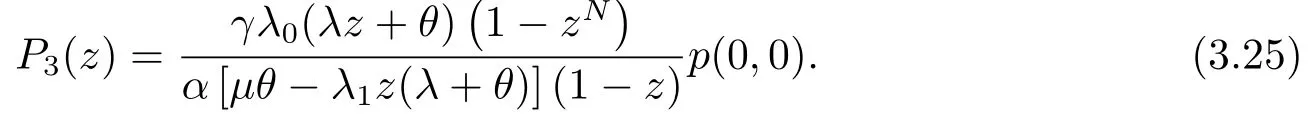
从(3.18)、(3.23)、(3.24)和(3.25)可以看到P0(z)、P1(z)、P2(z)和P3(z)均可以用p(0,0)来表示,再根据归一性,就可以计算出:
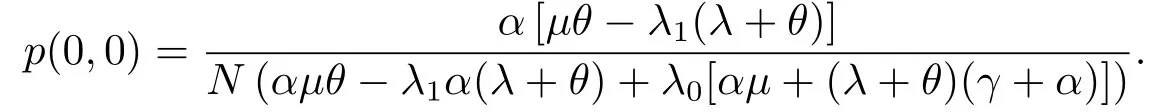
另外,通过对(3.18)、(3.23)、(3.24)和(3.25)分别对z求一阶导,然后取z =1,就可以得到(3.5)、(3.6)、(3.7)和(3.8).
设T(0,j),1 ≤j ≤N -1,T(1,j),j ≥0,T(2,j),j ≥1,和T(3,j),j ≥0分别表示一名标记顾客处于重试轨道中第j个位置,且服务台状态为i=0,1,2,3 的逗留时间.我们可以得到如下引理.
引理3.2对于带有N策略和不可靠服务台且拥有恒定重试率的M/M/1排队系统,若一名标记顾客处于重试轨道中第j个位置,且服务台状态为i = 0,1,2,3,则他的预期逗留时间分别为:

证通过分析我们可以得到如下等式:

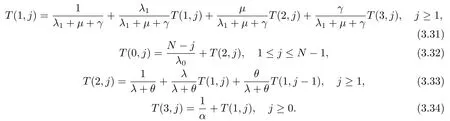
(3.30)式表示不可靠排队系统的广义服务时间(见文[17]).若一名标记顾客处于重试轨道中的第j个位置且服务台处于1状态,则他的预期逗留时间由以下几部分组成,首先他需要等待一段时间,这段时间表示接下来有新顾客到达并加入系统、正在被服务的顾客完成服务以及服务台损坏三者中有一个事件先发生的时间,且它服从参数为λ1+µ+γ的指数分布.若接下来以概率发生第一个事件,则该标记顾客的预期逗留时间变为T(1,j); 若接下来以概率发生第二个事件,则该标记顾客的预期逗留时间变为T(2,j); 若接下来以概率发生第三个事件,则该标记顾客的预期逗留时间变为T(3,j),通过上述分析,我们得到(3.31).利用相同的分析方法,我们可以得到(3.32)、(3.33)和(3.34).
接下来,将(3.33)和(3.34)带入(3.31),可以得到:
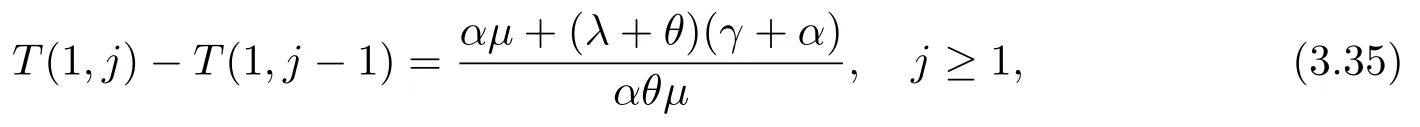
再结合(3.30),可以得到(3.27):

最后利用(3.27),再经过简单的计算,我们可以很容易得到(3.26)、(3.28) 和(3.29).
通过引理3.1和引理3.2,可以得到如下定理:
定理3.1对于带有N策略和不可靠服务台且拥有恒定重试率的M/M/1排队系统,若给定到达率(λ0,λ1,λ,0),则一个标记顾客到达瞬间发现服务台处于0状态或1状态并选择加入系统的平均预期逗留时间分别为:
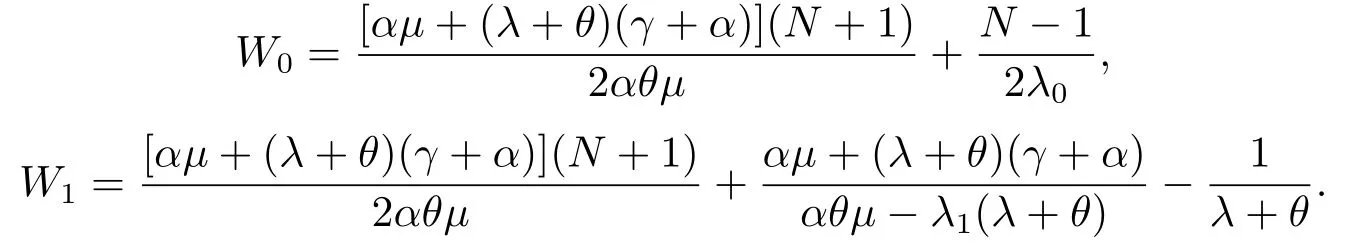
证设W0(k)示重试轨道中有k个顾客且服务台处于0 状态,一名顾客选择加入系统的预期逗留时间.很容易可以看出W0(k)可以用T(0,k+1) 来表示,即:W0(k) = T(0,k+1) =可由(3.26)得到.另设P(k|0)表示服务台处于0状态且重试轨道中有k个顾客的条件概率,即因此,一个标记顾客到达瞬间发现服务台处于0状态并选择加入系统的平均预期逗留时间为:
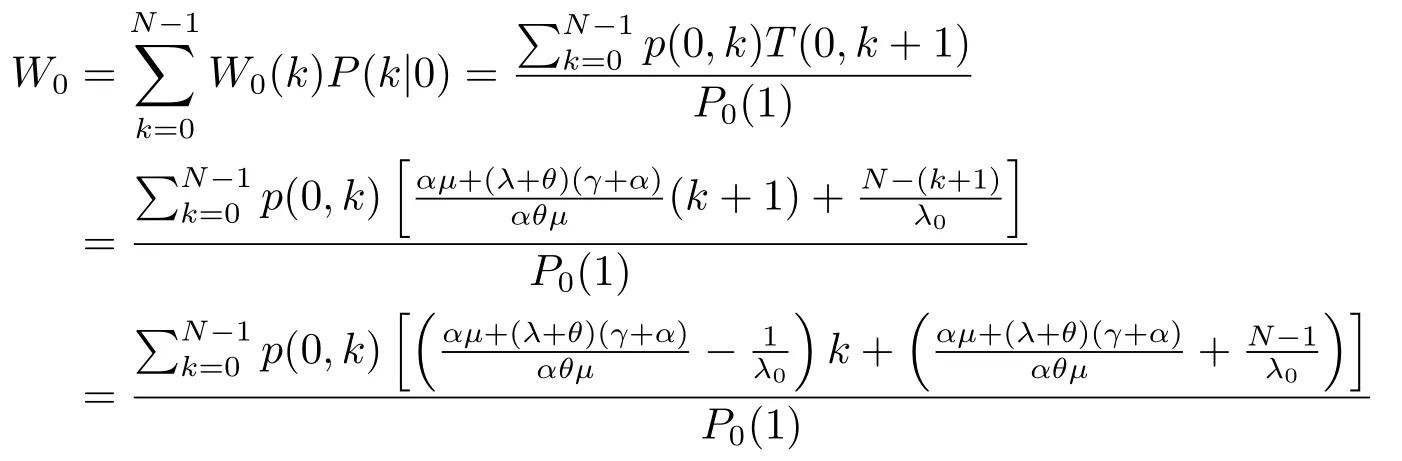

再由引理3.1我们就可以得到(3.36).同样的一个标记顾客到达瞬间发现服务台处于1状态且重试轨道中有k个顾客并选择加入系统的条件概率和平均预期逗留时间分别为:
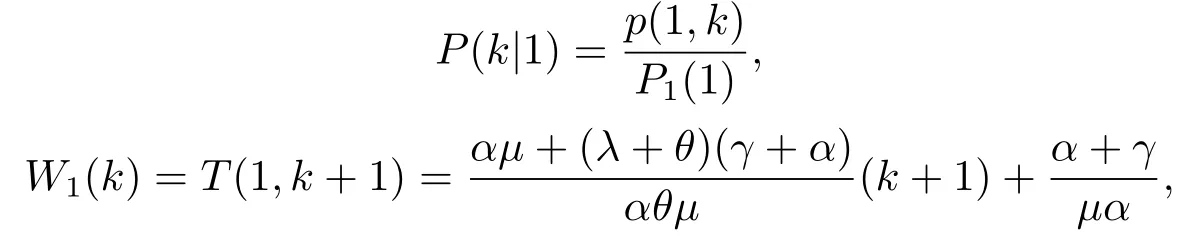
其中,P1(1)由引理3.1可得,T(1,k+1)由引理3.2可得.因此,一个标记顾客到达瞬间发现服务台处于1状态并选择加入系统的平均预期逗留时间为:
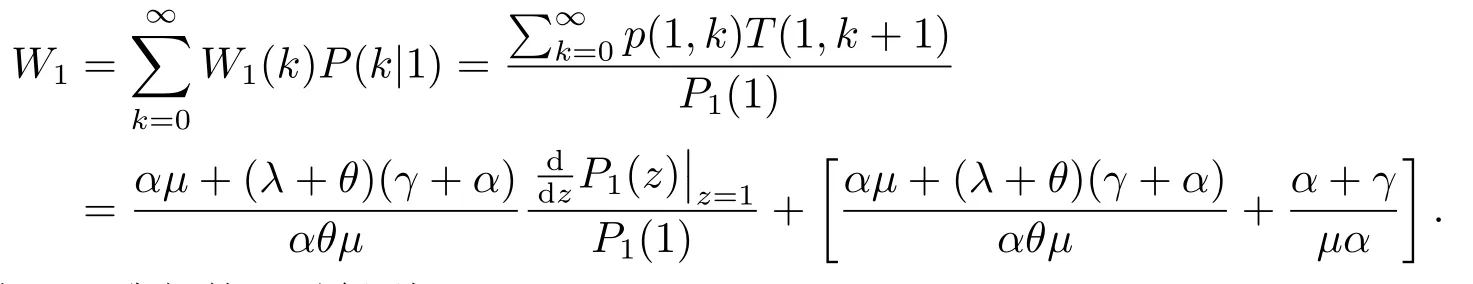
再次由引理3.1我们就可以得到(3.37).
从定理3.1很容易可以看出,平均预期逗留时间W0(或W1)是独立于λ1(或λ0)的,所以我们可以分别得到相应的均衡到达率(唯一均衡或多元均衡).而且,在接下来的定理3.2可以发现拥挤偏好(FTC)情形和拥挤厌恶(ATC)情形在某些情况下是存在的.
定理3.2对于带有N策略和不可靠服务台且拥有恒定重试率的M/M/1排队系统,当服务台处于休眠状态(i=0)时,顾客均衡到达率如下:
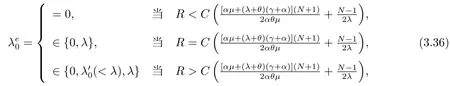
当服务台处于繁忙状态(i=1)时,顾客均衡到达率如下:
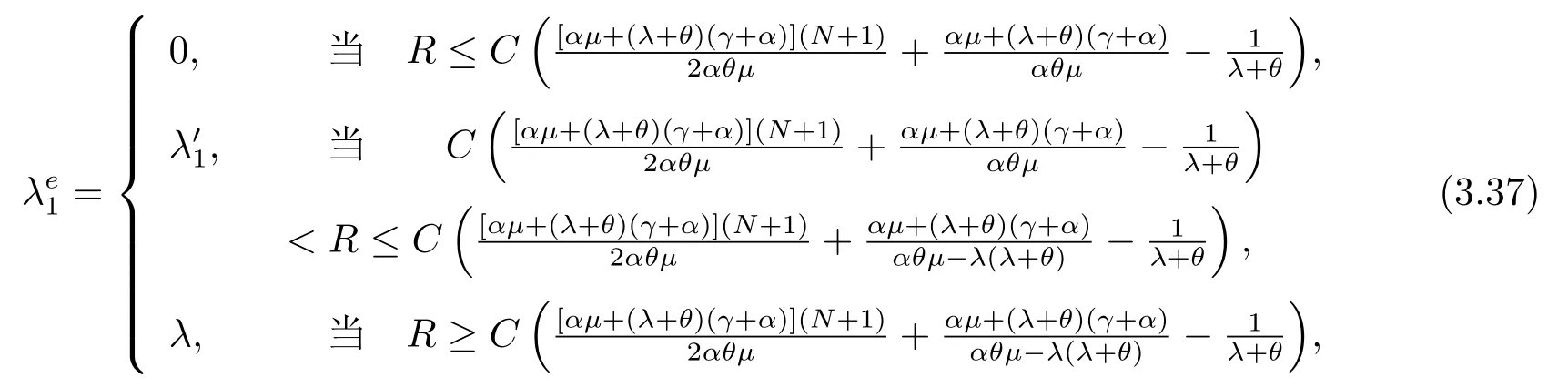
其中,

证首先,一名顾客到达时发现服务台处于休眠状态,止步总是一种均衡策略,因为如果其它所有顾客均选择止步,则服务台永远不会被激活,那么对于标记顾客来说此时止步是最好的选择.所以,λe=0总是一个均衡到达率且与R无关.
我们现在来考虑当标记顾客到达时发现服务台处于休眠状态的正的均衡到达率.根据收益函数的结构,标记顾客选择加入系统的净收益等于他完成服务获得的奖励R与逗留总花费之差,所以根据定理3.1,我们可以得到标记顾客预期净收益为:
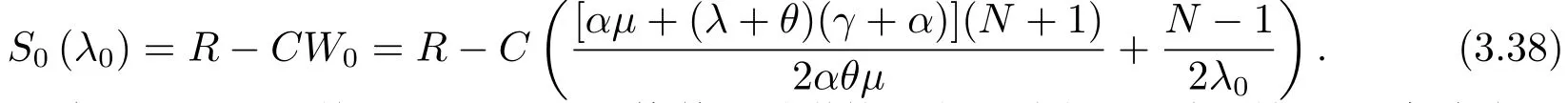
我们可以看出,S0(λ0)是关于λ0∈[0,λ] 严格单调递增的,所以,我们可以得到如下几个结论:
同样的,根据定理3.1,如果一名到达顾客发现服务台处于繁忙状态且决定加入系统,他的预期净收益为:
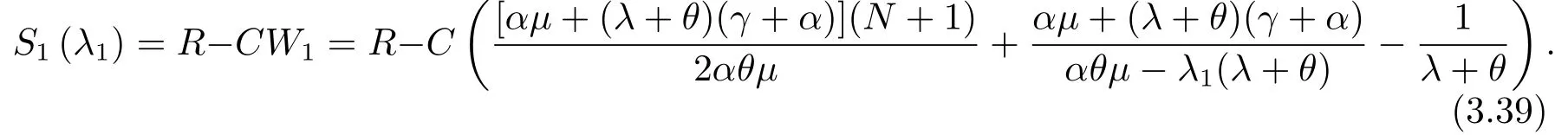
另外,(3.39)的证明过程同上述(3.38)的证明过程.
注3.1因为S1(λ1)是关于λ1∈[0,λ]的减函数,一方面,当顾客到达率为λ1且λ1>时,若标记顾客到达并选择加入系统,则他的预期净收益为负值,因此,此时标记顾客的唯一最优决策是止步(λ1=0),另一方面,当顾客到达率为λ1且λ1<时,若标记顾客到达并选择加入系统,则他的预期净收益为正值,因此,此时标记顾客的唯一最优决策是加入(λ1=λ).上述分析表明了: 标记顾客的最优决策是关于其它顾客所采用决策的减函数,即: 其它顾客的到达率越高,则标记顾客的最优到达率越低,这是拥挤厌恶(ATC)情形,所以至少存在一个均衡到达率.另外要注意唯一均衡到达率λ′1是稳定的,因为W1是关于λ1∈[0,λ]的增函数,所以顾客到达率λ1的增加会使得平均预期逗留时间的增加,这样就会导致选择加入系统的顾客变少,所以顾客到达率λ1的增加就会得到遏制,因此唯一均衡到达率就会逐渐趋于一个稳定的值.同样的,我们很容易可以看出来S0(λ0)是关于λ0∈[0,λ]的增函数,应用上述相同的分析方法,可以得到它对应的是拥挤偏好(FTC)情形,所以多元均衡到达率可能存在且均衡到达率是不稳定的.
4.社会收益
社会收益等于所有顾客预期净收益之和,所以要求社会最优到达率,需要将所有顾客看作一个整体并且使得社会收益最大化.首先,我们给出社会收益函数S(λ0,λ1) 的表达式,然后寻找使它最大化的参数(服务台处于0状态时的社会最优到达率)和(服务台处于1状态时的社会最优到达率).
定理4.1社会收益函数表达式如下:
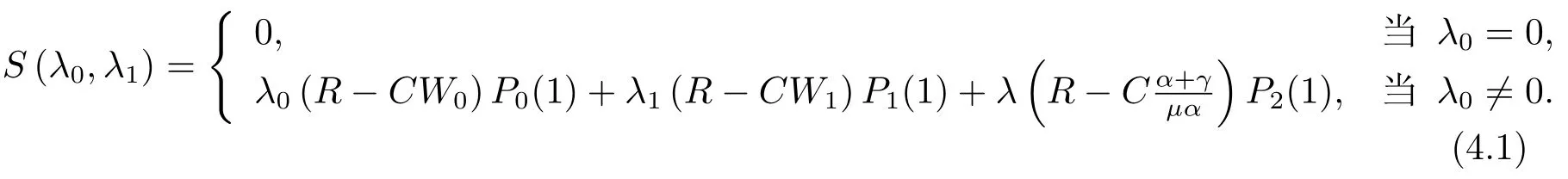
其中,P0(1)、P1(1)和P2(1)由引理3.1可得,W0和W1由定理3.1可得.
证如果λ0= 0,则服务台永远处于休眠状态,不会被激活,所以此时社会收益为0,得到(4.1)第一部分; 如果λ00,根据社会收益的定义,社会收益函数等于所有顾客的预期净收益之和,即:
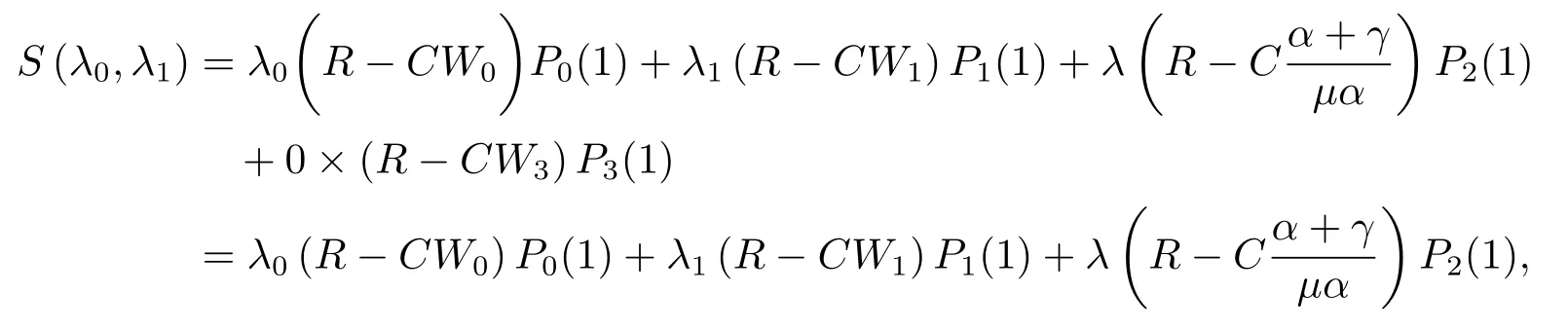
得到(4.1)的第二部分.
注4.1通过计算,可以得到这说明当服务台处于休眠状态且顾客到达时间间隔趋于无穷大的时候,社会收益会为负值.这种现象可以从管理者的角度理解,当顾客到达率为无穷小的时候,管理者关闭系统是最好的选择.
注4.2当θ →∞时,即重试时间趋于0,这个时候我们所研究的系统可以看作是一个带有N策略和不可靠服务台的M/M/1排队系统.
因为求得S(λ0,λ1)的表达式非常复杂,通过传统的计算很难得到相应的结果,所以,在后一节中我们采用粒子群优化算法(PSO)得到和的值.
PSO算法最先由Kennedy和Eberhart在1995年提出,它有精度高、收敛速度快等特点,使用它我们不需要对目标函数做太多的分析,可以很容易找到全局最优解,这些特性刚好是我们所需要的,下面就简单介绍一下PSO 算法的要点.
首先,需要设置如下几个参数: 最大迭代次数、目标函数的自变量个数和粒子的最大速度,其中每个粒子只具有两种属性: 速度和位置,速度代表粒子移动的快慢,位置代表粒子移动的方向.开始时位置信息会设置为整个搜索空间,并且会在速度区间和搜索空间上随机初始化粒子的速度和位置,然后不断迭代更新粒子的速度和位置,同时得到每个粒子的最优解(个体极值),再从这些个体极值中找到一个最优解称为本次全局最优解,将它再与历史最优进行比较,不断更新,最后,就能得到我们所需要的全局最优.
速度和位置更新公式如下:

其中,ω称为惯性因子,较大时,算法全局寻优能力强,局部寻优能力弱,较小时,算法全局寻优能力弱,局部寻优能力强,所以,通过调整ω的大小,可以对算法全局寻优能力和局部寻优能力进行调节.c1和c2称为加速常数,前者称为每个粒子的个体学习因子,后者称为每个粒子的社会学习因子.pid表示第i个变量的个体极值的第d维,pgd表示全局最优解的第d维.
本文中,我们设置ω =0.9,c1=c2=2,粒子数S =100,最大迭代次数M =2000.尽管迭代次数不够大,但重复了6次发现结果几乎一样.
5.数值结果
本节中,我们主要基于PSO算法研究不同参数(N,R,θ,µ,α,γ)对社会收益函数S(λ0,λ1)的影响,导出了的数值最优解进而得到然后再对系统性能指标的敏感性进行分析.

图5.1 社会最优到达率()和社会收益S()关于N的变化(λ=1,µ=θ =3,α=γ =1,R=8,C =2)
综上所述: 如果社会管理者想得到一个较高的社会收益,他就必须设置N为一个相对较小的值.我们在图5.1(b)中可以看到,当N = 1 时,社会收益达到最大值,也就是说,当一名顾客到达时发现服务台处于休眠状态并选择加入系统,系统就会被立即激活,这种情况下系统的社会收益达到最大值.
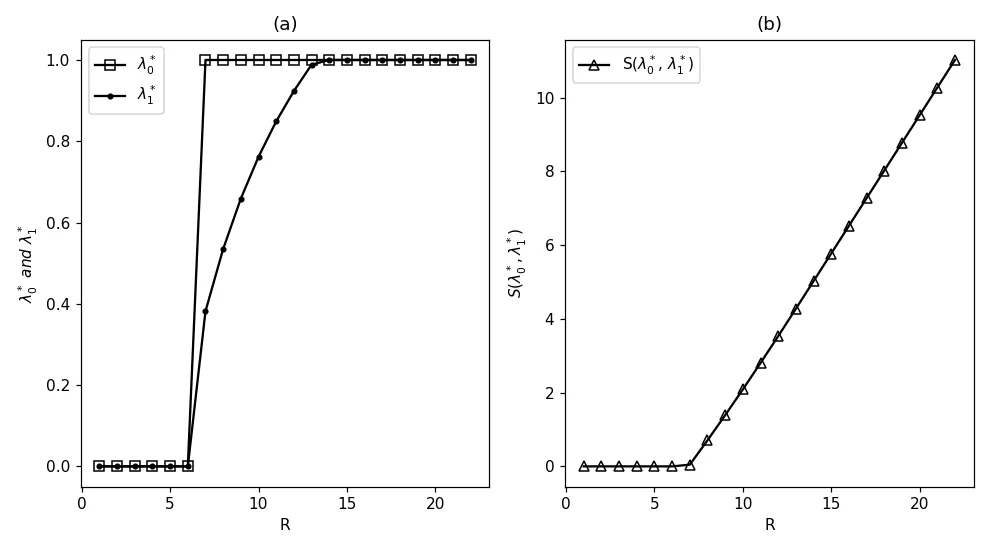
图5.2 社会最优到达率()和社会收益S()关于R的变化(λ=1,µ=θ =3,α=γ =1,N =4,C =2)
图5.2(b)显示: 当R = 1,2,3,4,5,6时,S() = 0,当R >6时,S变为正值且逐渐变大.
综上所述: 后到顾客带来的正收益将弥补早到顾客的损失,所以从整体来看,所有顾客的社会收益都是正值,因此,如果社会管理者想要获得一个较高的社会收益,他需要设定一个相对较大的R,鼓励更多的顾客选择加入系统.
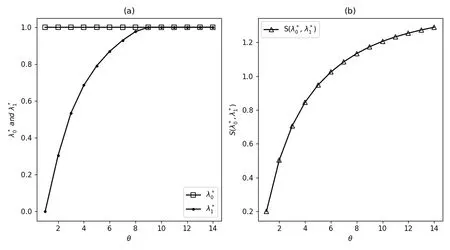
图5.3 社会最优到达率和社会收益关于θ的变化(λ=1,µ=3,α=γ =1,N =4,R=8,C =2)
综上所述: 社会管理者如果想获得一个较大的社会收益,则他需要设定相对较大的θ.
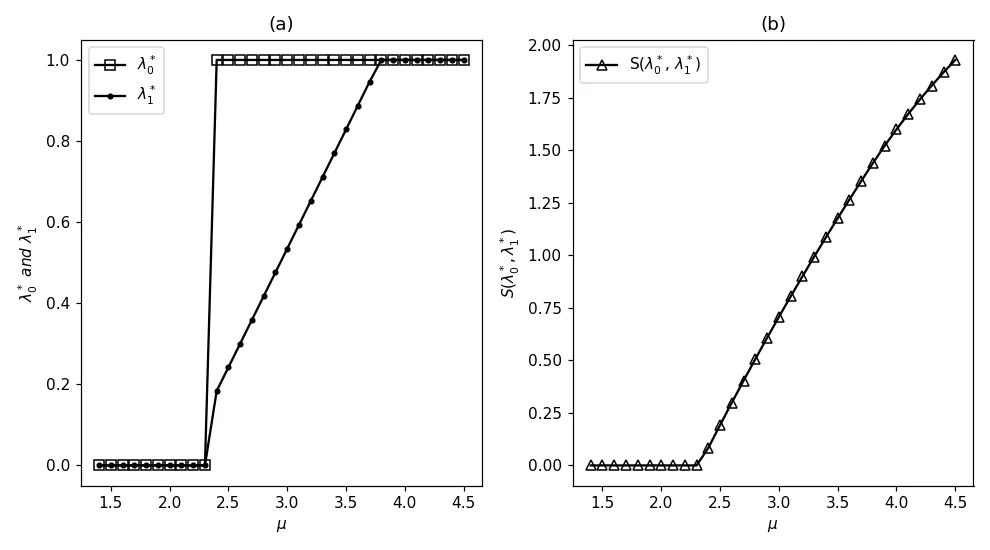
图5.4 社会最优到达率()和社会收益S()关于µ的变化(λ=1,θ =3,α=γ =1,N =4,R=8,C =2)
综上所述: 若社会管理者希望系统被激活以后有更多的顾客选择加入系统,以获得较高的社会收益,他需要设置µ>2.4.
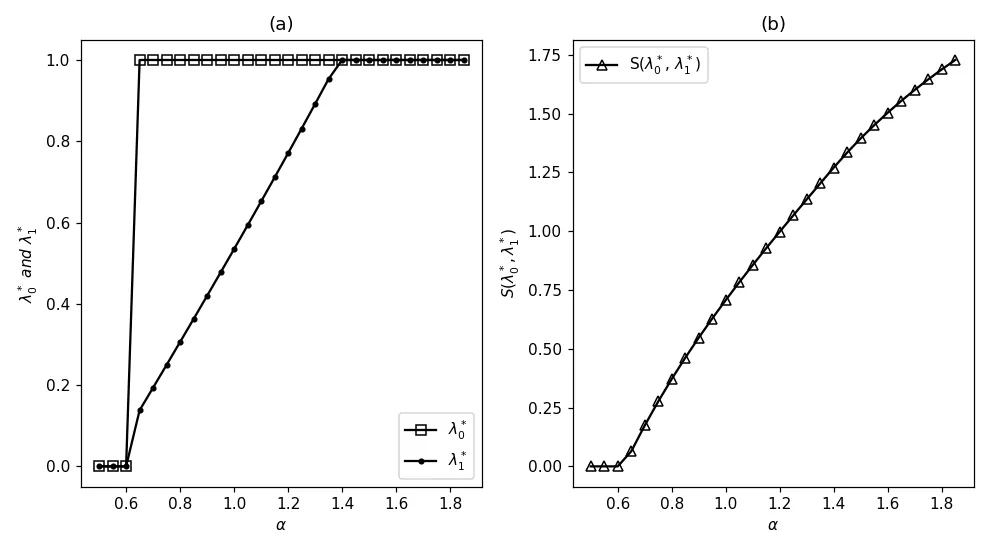
图5.5 社会最优到达率(,)和社会收益S(,)关于α的变化(λ=1,µ=θ =3,γ =1,N =4,R=8,C =2)
综上所述: 若社会管理者希望获得较高的社会收益,他需要设置α >0.6.
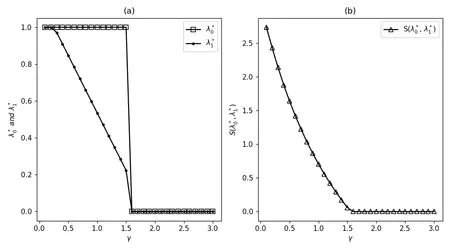
图5.6 社会最优到达率(,)和社会收益S(,)关于γ 的变化(λ=1,µ=θ =3,α=1,N =4,R=8,C =2)
综上所述: 若社会管理者希望获得较高的社会收益,则他必须保证服务台的“质量”,使服务台“寿命”尽可能的长.
猜你喜欢
杂志排行
应用数学的其它文章
- New Iteration Method for a Quadratic Matrix Equation Associated with an M-Matrix
- 具有随机保费和交易费用的最优投资-再保险策略
- A Smoothing Newton Algorithm for Tensor Complementarity Problem Based on the Modulus-Based Reformulation
- The Center Problems and Time-Reversibility with Respect to a Linear Involution
- Boundary Value and Initial Value Problems with Impulsive Terms for Nonlinear Conformable Fractional Differential Equations
- 具有比例依赖的非自治捕食者-两互惠食饵系统的动力学行为
