指数-伽马模型下在险价值和条件在险价值贝叶斯估计的中偏差原理

严钧，章熙尧

( 扬州大学数学科学学院，江苏 扬州225002)

1.引言

在险价值(VaR，Value-at-Risk)和条件在险价值(CVaR，conditional Value-at-Risk)是两种常用的风险度量.Jorion[1]较完整地描述了VaR的定义，通过进一步研究推广而广泛的用于风险度量领域[2-5].由于VaR具有一些缺点，例如不满足次可加性且忽略了分位点的信息，仅考虑了预期最大损失.所以人们引入了风险度量CVaR[6]，它不仅满足平移不变性，次可加性，正齐性以及单调性，而且具有VaR特有的性质[7-8].设X为定义在概率空间(Ω，F，P)上的随机变量，累积分布函数为F.X的水平α的VaR定义为

其中，F-1(s)=inf{t;F(t)≥s}为分布函数F的广义反函数.X的水平为α的CVaR定义为

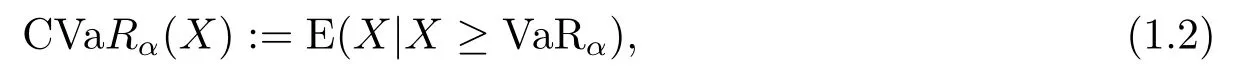
等价地[9]

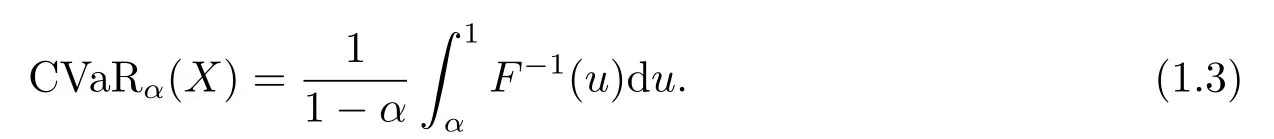
特别地，如果X服从密度为θe-θx，x ＞0的指数分布，则

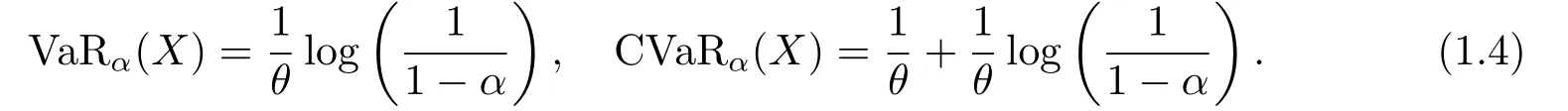
在金融市场中，参数θ反映了随机变量X的风险特征，考虑到风险的非齐次性[10]，不妨假定θ为随机变量，满足某种先验分布，此时对风险X的度量和评估落入贝叶斯框架[11].章溢等[12]考虑了指数-伽马模型下VaR的贝叶斯估计的渐近性质.具体地，设θ服从密度为π(θ)=(βλ/Γ(λ))θλ-1e-βθ，θ ＞0，设在θ给定的条件下，X1，X2...，Xn独立同分布，它们共同的密度为f(x|θ)=θe-θx，x ＞0.章溢等[12]构造了如下的估计量

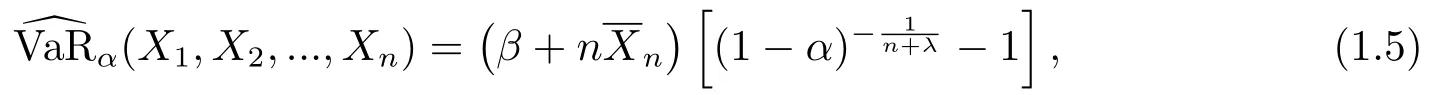
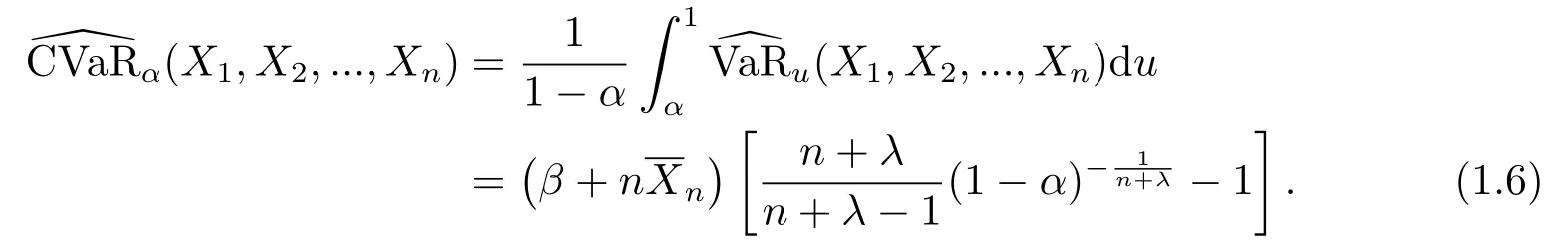
风险度量估计量的渐近行为的研究是风险管理的热点问题.GAO[13]研究了经验CVaR的大偏差原理和中偏差原理，XING[14]研究了投资组合损失的尾部失真风险度量和各个资产损失的在险价值之和的渐近比率，CAI[15]研究了几种风险度量的渐近等价性.受这些研究结果的启发，本文研究两个贝叶斯估计量(X1，X2，...，Xn) 和(X1，X2，...，Xn) 的中偏差原理.

2.指数-伽马模型下VaR和CVaR贝叶斯估计的中偏差原理

定理2.11)-VaRα(X)，n ≥1} 满足速度函数为速率函数为V(x)的中偏差原理

即对于任意的A ⊆R

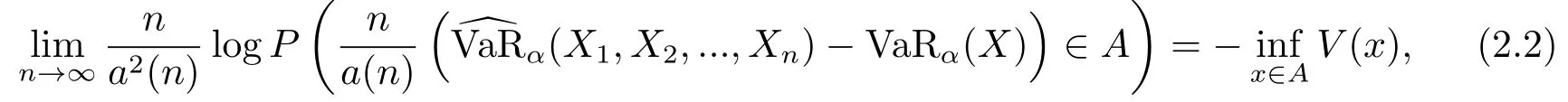
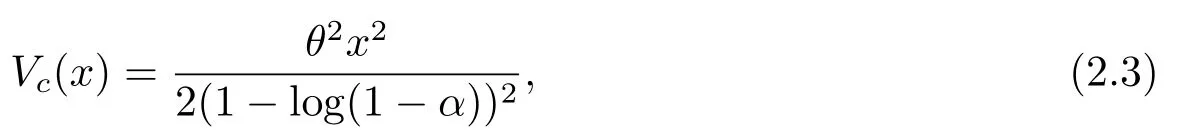
即对于任意的B ⊆R

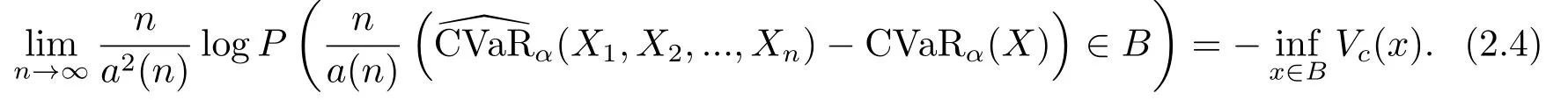
证1) 根据大偏差理论[16]，我们需要计算

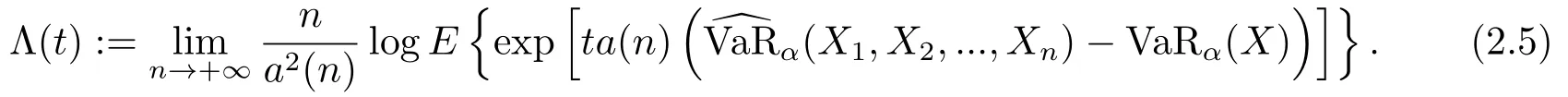
事实上，

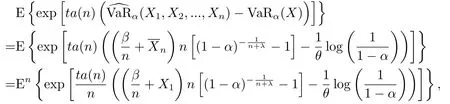
由Taylor展开

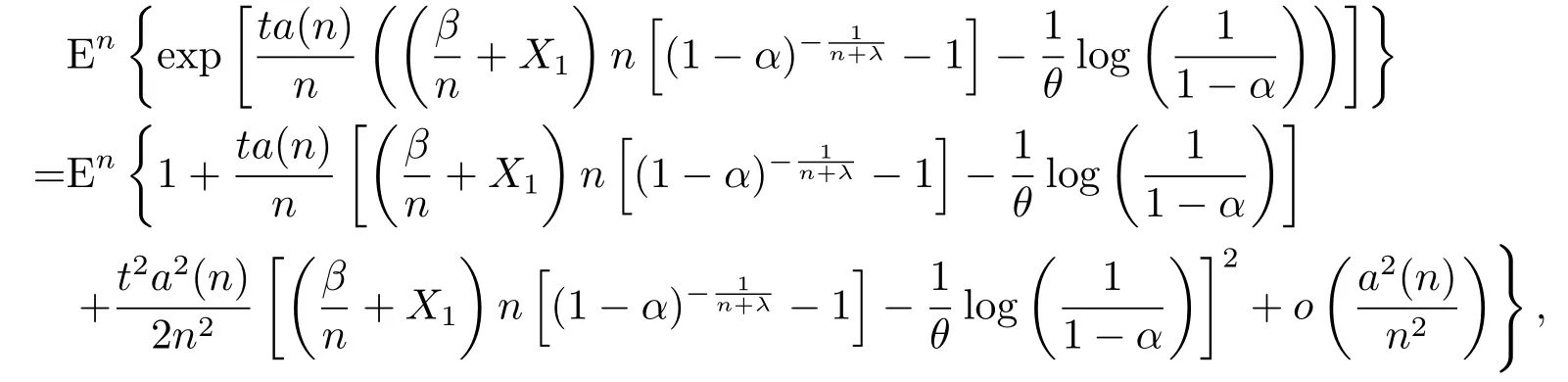
所以

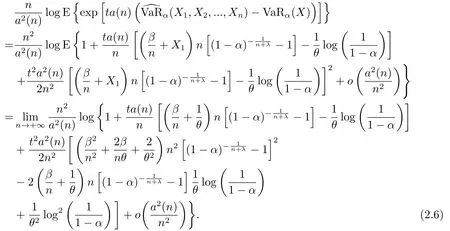
由于

所以

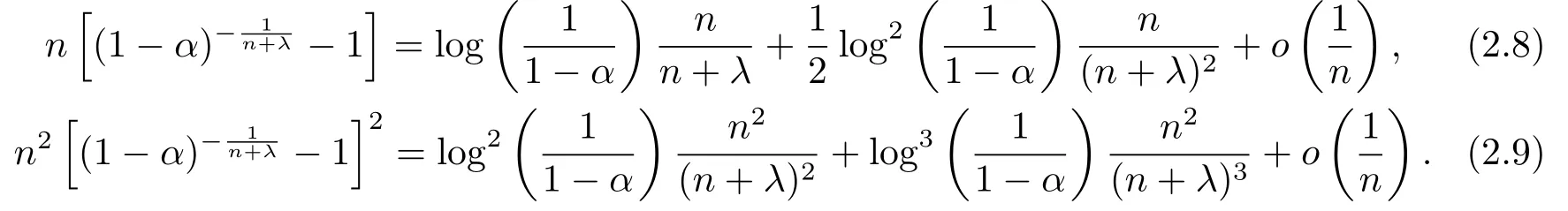
进一步

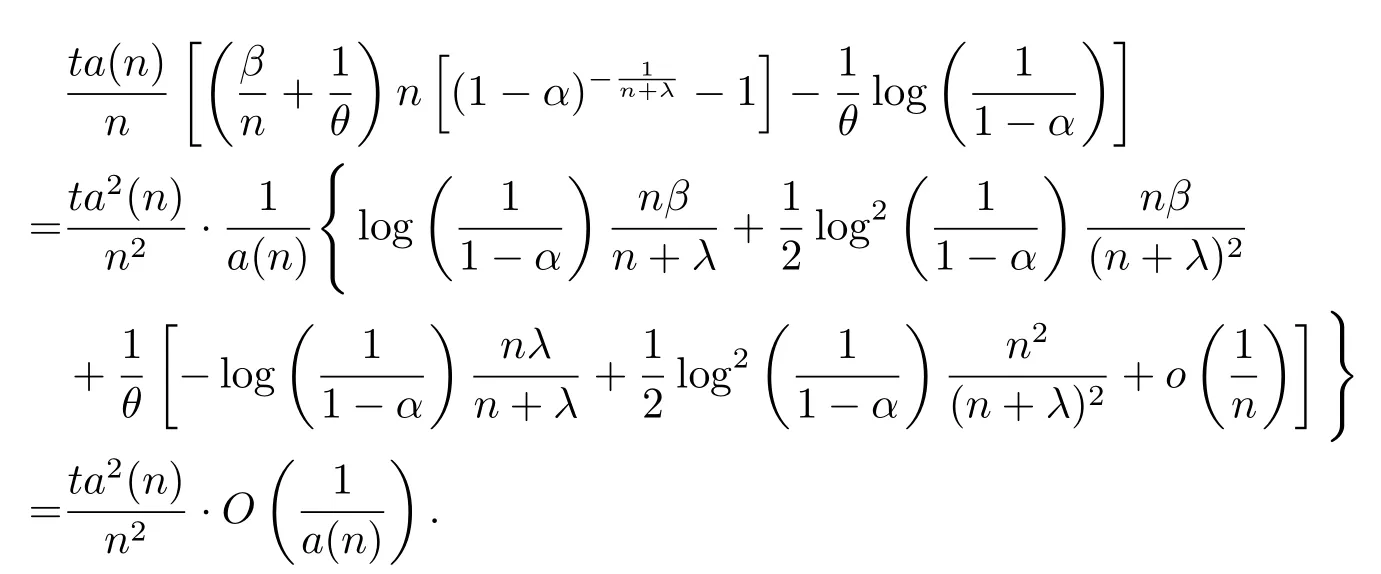
同理

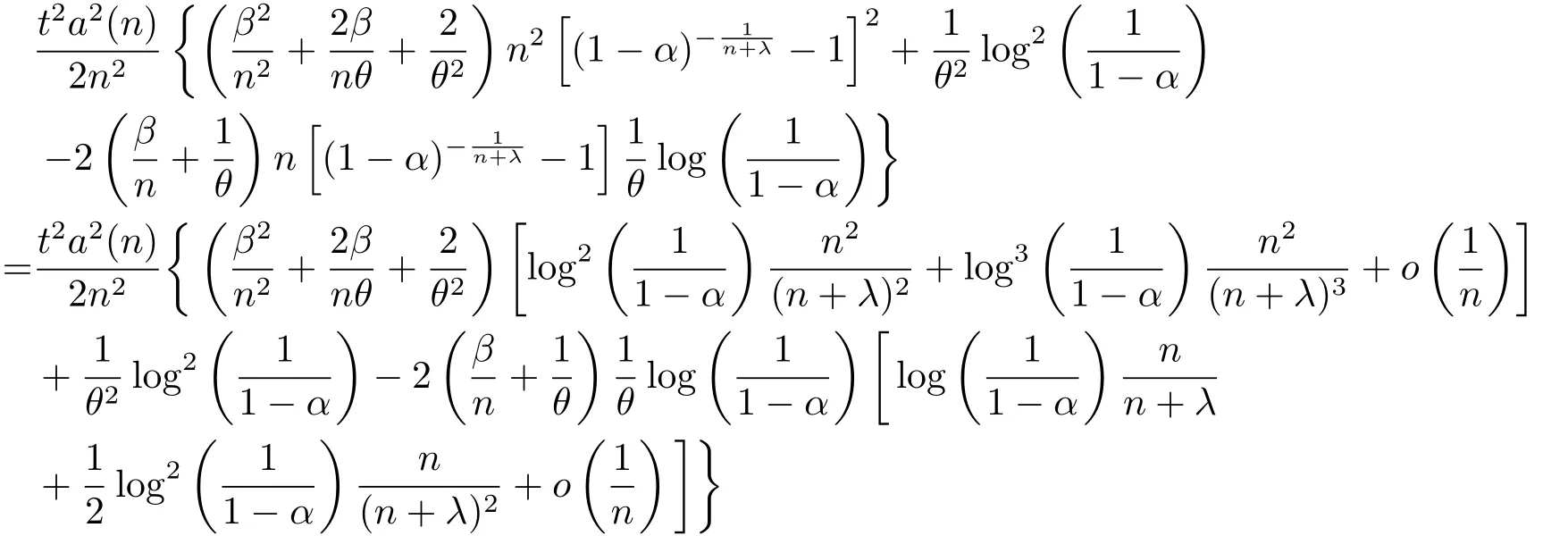
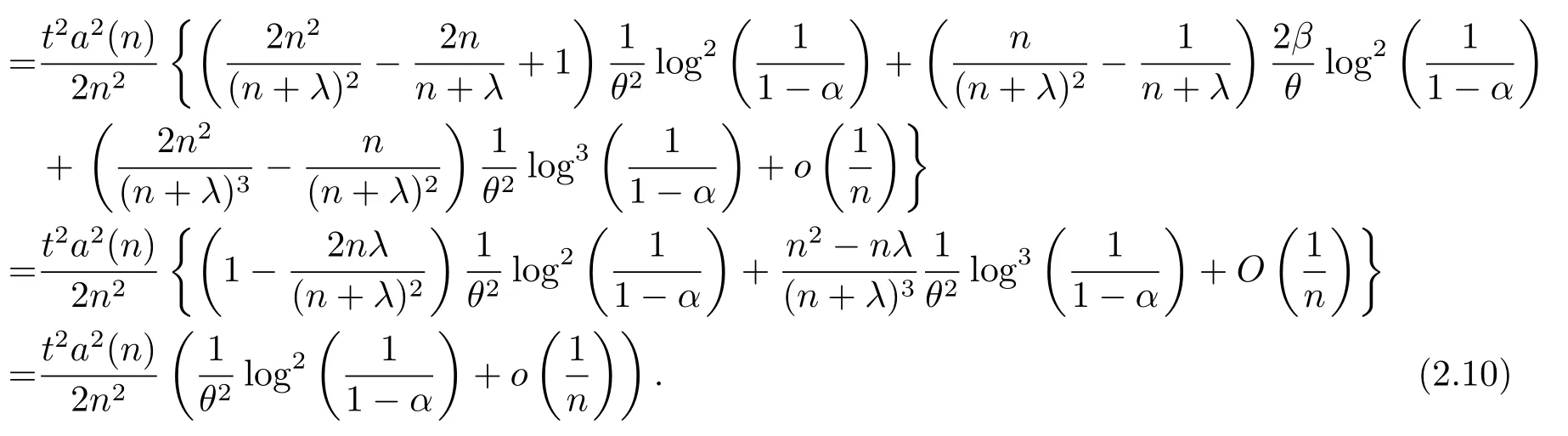
因此

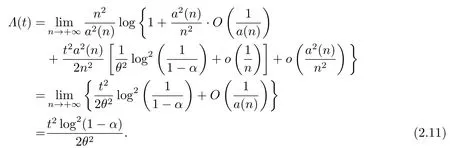
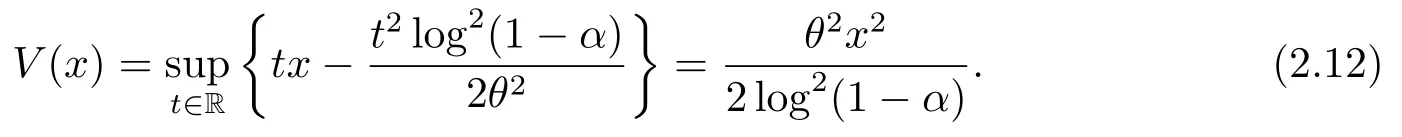
2) 证明与1)类似，故省略具体的证明过程.

3.数值模拟

下面我们给出主要结果的随机模拟，具体地，在定理2.1中，取A=B =(-∞，ϵ]∪[ϵ，+∞)，ϵ＞0，则有

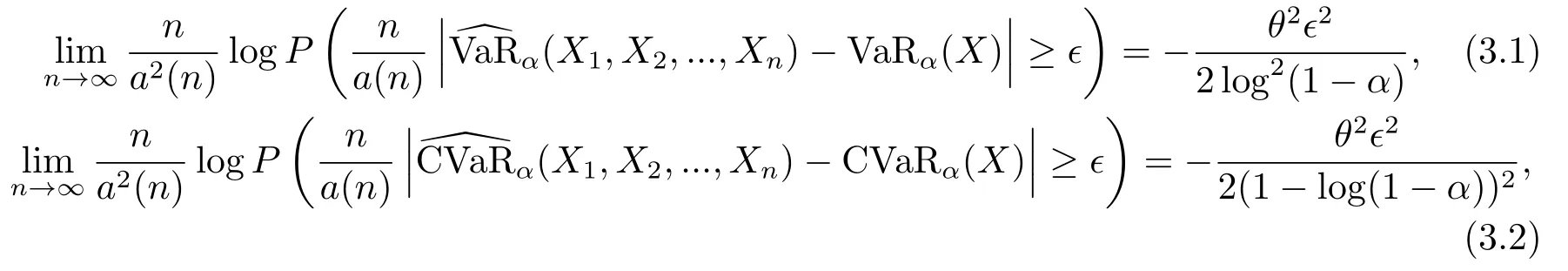
即对于充分大的n，有

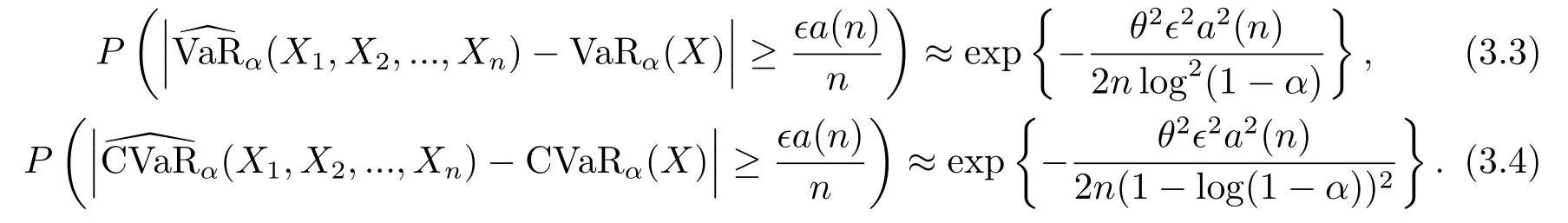
取

1) α=0.95，ϵ=0.1，λ=4，β =2;

2) θ 取1000个服从Γ(4，2)随机数的中位数;

3) a(n)=n0.99.

为了方便，记

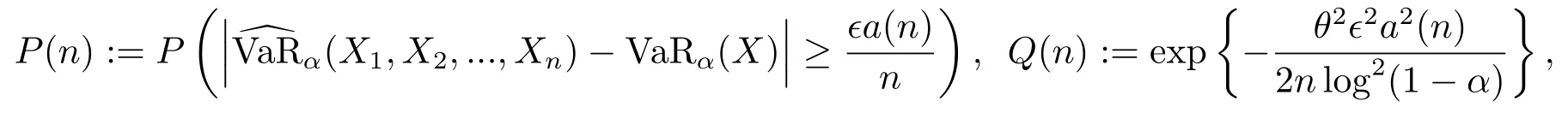
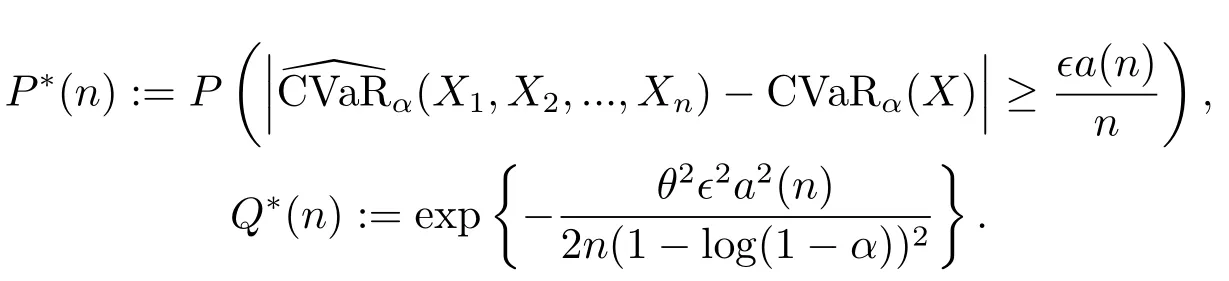
模拟结果如下:

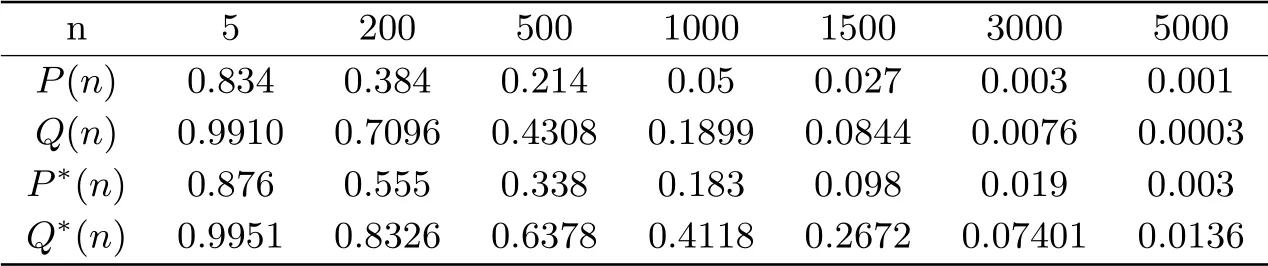
表3.1 P(n)，Q(n)，P*(n)，Q*(n)的模拟结果

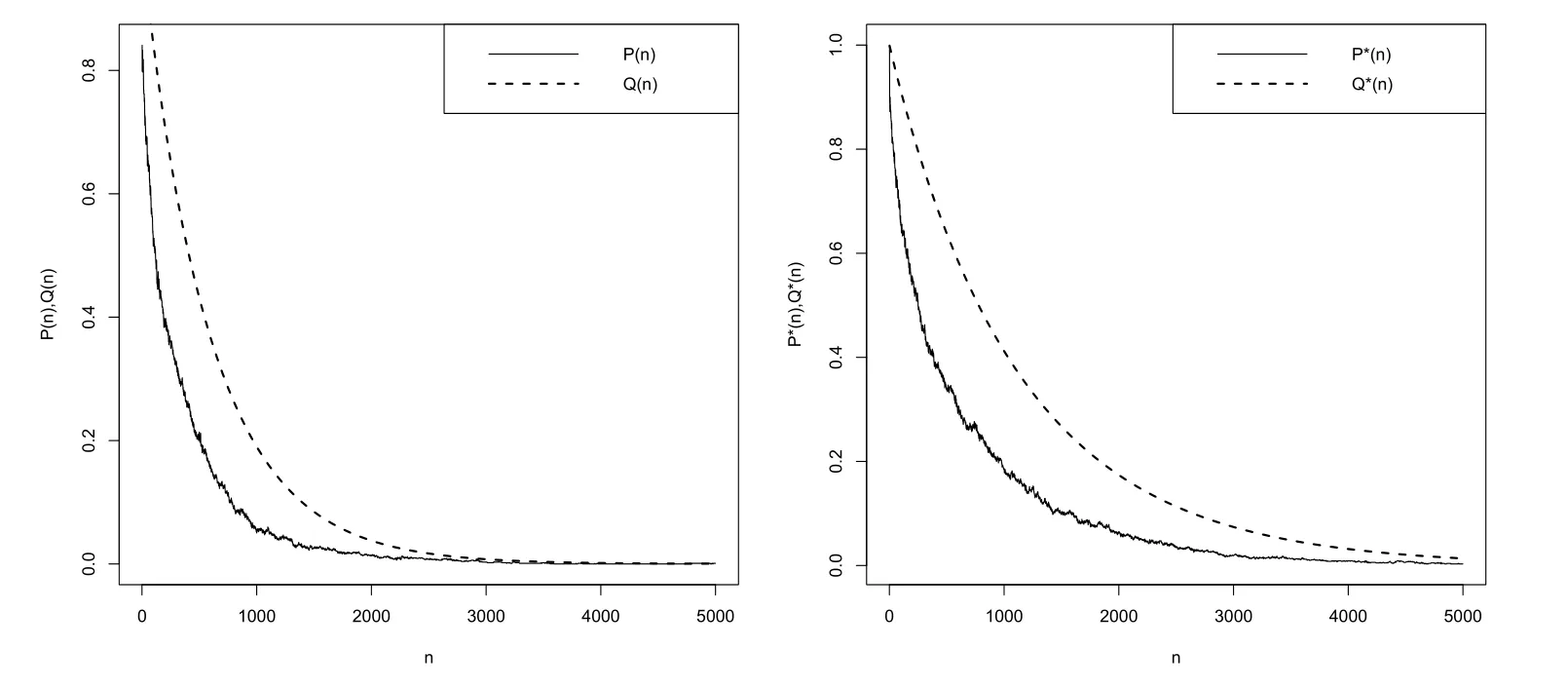
图3.1 P(n)和Q(n)的模拟结果(左图)与P*(n)和Q*(n)的模拟结果(右图)

图3.1左边为P(n)和Q(n)的模拟结果，显然P(n)趋向于0，当n充分大时，P(n)和Q(n)吻合情况很好；右边为P*(n)和Q*(n)的模拟结果，P*(n)同样趋向于0，当n充分大时，P*(n)和Q*(n)吻合情况也很好.