次线性期望空间下行END阵列的完全收敛性
2021-01-07占周婷吴群英
占周婷,吴群英
( 桂林理工大学理学院,广西 桂林541004)
1.引言及引理
随着社会和科学的发展,极限理论被广泛的应用到统计、经济和金融等领域中.经典极限理论是在模型确定的条件下成立,然而模型确定性假设在现实生活中许多应用领域是不成立的,因为不确定性现象无法用确定性模型解释.在经典极限理论中,概率和期望是具有可加性的,而现实生活中很多不确定现象不符合线性可加的条件.因此为解决经典极限理论在应用方面受到的限制,彭实戈院士[1]引入了次线性期望空间理论,并给出了次线性期望理论的完整公理体系.次线性期望是经典线性期望的延伸,近几年一系列新的研究结果被大量应用于统计、金融、经济和风险度量等方面.如PENG[2]证明了次线性期望下的中心极限定理;ZHANG[3-5]研究了次线性期望下END序列的Kolmogorov强大数定律、矩不等式、重对数律以及独立和ND情况下的Rosenthal’s不等式; WU和JIANG[6]研究得到次线性期望下的强大数律与Chover’s型重对数律; HU[7]研究得到次线性期望空间下一般矩条件的强大数律;WANG和WU[8]研究了次线性期望下行END阵列的完全收敛性.
完全收敛性最初是由统计学者HSU和ROBBINS[9]在1947年提出,至此吸引了广大学者的兴趣.现如今,经典概率空间中关于完全收敛性的研究成果已经硕果累累.如KATE[10]和BAUM[11]得到了独立同分布随机变量部分和完全收敛的充分必要条件; 白志东和苏淳[12]加强并改进了KATE和BAUM独立同分布随机变量部分和完全收敛性的研究结果; WU[13-14]分别给出了ND序列和ND阵列随机变量完全收敛性的证明; 孟兵和吴群英[15]证明了ND阵列加权乘积和的完全收敛性; YI等[16]研究了NOD序列加权和的完全收敛性; SUNG[17]运用指数不等式得到了一个针对于独立随机变量阵列的新的完全收敛的结果; HU[18]等得到了行END阵列的完全收敛性.在次线性期望下虽然有LI和WU[19]证明了广义独立阵列的完全收敛和完全积分收敛性.但作为一种诞生不久的理论,次线性期望空间中关于极限理论的研究还需大量投入与输出.本文在现有的理论基础上,进一步将文[18]中定理3.1从概率空间中行END阵列的完全收敛性推广到次线性期望下行END阵列的完全收敛性,并且进一步扩展了条件范围得到相应的结果.
我们使用彭实戈院士[1-2]提出的次线性期望空间的框架,假设(Ω,F)是给定的可测空间,H是定义在(Ω,F)上由实函数构成的线性空间,使得如果X1,X2,··· ,Xn∈H,则对于任意的φ ∈Cl,Lip(Rn)有φ(X1,X2,··· ,Xn) ∈H,其中Cl,Lip(Rn)表示在线性空间的局部Lipschitz函数,即对任意φ ∈Cl,Lip(Rn),存在常数c >0,m ∈N取决于φ,都有

也称H是由随机变量所构成的空间,并记X ∈H.
定义1.1[4]在空间H上的如果对任意的X,Y ∈H满足以下四个条件:

定义1.2[4]令G ⊂F,如果函数V :G →[0,1]满足以下两个条件:
1) V(∅)=0,V(Ω)=1;
2) 对任意A ⊂B,A,B ∈G,则有V(A)≤V(B).
则称V 为容度.如果对所有的A,B ∈G,有V(A ∪B)≤V(A)+V(B),则称V 具有次可加性; 如果对任意An∈F,有则称V 具有可数次可加性.
在次线性期望空间中对上容度V和下容度V的定义如下:

其中,Ac为A的的补集.因此根据定义很容易可以看出V具有次可加性,且
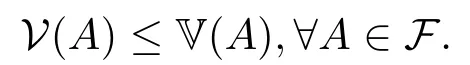
如果I(A)∈H,有
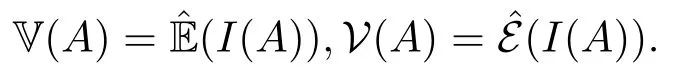
如果f ≤I(A)≤g,f,g ∈H,则有
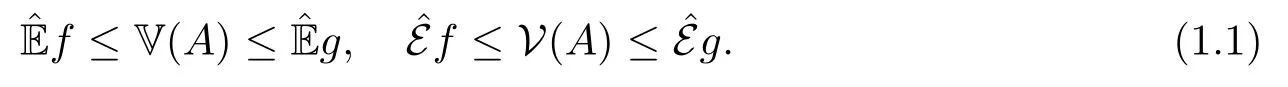
对于∀X ∈H,p >0,x >0,因为


成立.
定义1.3[4]定义Choquet积分为
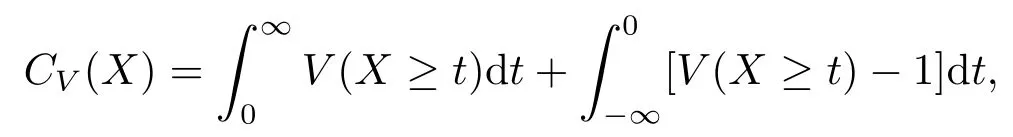
其中V 可由上容度V和下容度V替换.
定义1.4[3](END) 在次线性期望空间(Ω,H,)下随机变量序列{Xn;n ≥1}被称为END随机变量序列,如果存在常数K ≥1,使得对任意的属于Cb,Lip(R)的非降(或非增)的非负函数φi,都有

成立.
设{kn;n ≥1}是正整数序列,如果对任意固定的n ≥1,{Xni;1 ≤i ≤kn}是END序列,则称{Xni;1 ≤i ≤kn,n ≥1}为行END阵列.
显然,根据END随机变量序列的定义很容易可以得到,如果{Xn;n ≥1}是END随机变量序列,f1(x),f2(x),··· ∈Cl,Lip(R)是非降(或非增)的函数,则{fn(Xn);n ≥1}也是END随机变量序列.
本文约定,C总代表一个正常数,在不同的地方可取不同的值; an≪bn表示存在常数C使得对充分大的n都有an≤Cbn; I(·)表示示性函数.
为证本文的结论,我们需要下面的引理.
引理1.1[3]设{Xn;n ≥1}是次线性期望空间下的END随机变量序列,且0,令则

且对任意的p ≥2,存在常数Cp≥1,使得

其中K是END随机变量序列定义中的控制常数.
引理1.2设{Xn;n ≥1}是次线性期望空间下的END随机变量序列,且Xk≤0,令且存在y >0使得|Xk|≤y,则对任意的x >0,n ≥1和0 <p ≤2,都有

其中K的定义同(1.4).
证由END序列的定义可知,对任意的t >0,{etXk;k ≥1}也是END序列,则有

对t >0和0 <p ≤2,定义函数k(x) = (etx-1-tx)/xp,∀x >0,则容易证得k(x)在x >0上单调递增.因此当t >0和0 <p ≤2 时,函数k(x)=(etx-1-tx)/xp,∀x >0是增函数,以及|Xk|≤y可得

又由ex>x+1,∀x >0可得

因此由(1.2)和(1.6)式可得
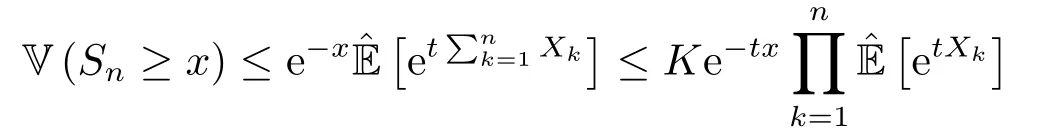

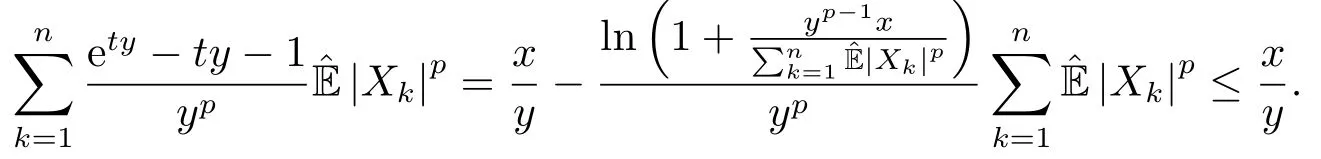
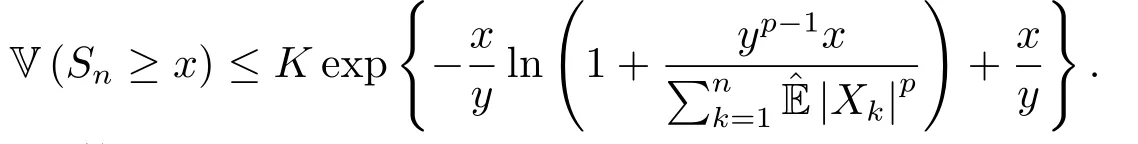
所以就完成了引理1.2的证明.
2.主要结果及其证明
在次线性期望空间中,由于次线性期望和容度不再具有可加性,所以对次线性期望空间的完全收敛性的研究与经典概率空间的相比有所不同,且更具挑战性.
假设{Xni;1 ≤i ≤kn,n ≥1} 是次线性期望空间下的行END随机变量阵列,{kn}是正整数序列,{an;n ≥1}是非减的正常数序列.由END序列的定义可知,为了确保截尾后的随机变量阵列也是行END阵列,需采用定义在Cl,Lip(R)上的非减函数或非增函数来进行截尾.令fb(x)=-bI(x <-b)+xI(|x|≤b)+bI(x >b),∀b >0.
对ε >0 和λ >0,令
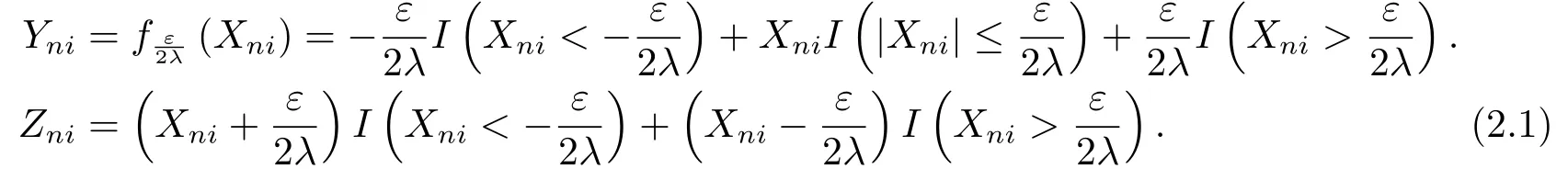
显然Xni=Yni+Zni.因为fb(x)∈Cl,Lip以及fb(x)是非减的,所以{Yni;1 ≤i ≤kn,n ≥1}也是行END 随机变量阵列.
定理2.1假设{Xni;1 ≤i ≤kn,n ≥1}是次线性期望空间下的行END随机变量阵列,{kn;n ≥1}是正整数序列,{an;n ≥1}是非减的正常数序列,其中{Yni;1 ≤i ≤kn,n ≥1}由(2.1)定义,如果

存在λ >0和0 <p ≤2或者0 <λ ≤1和p >2使得

则

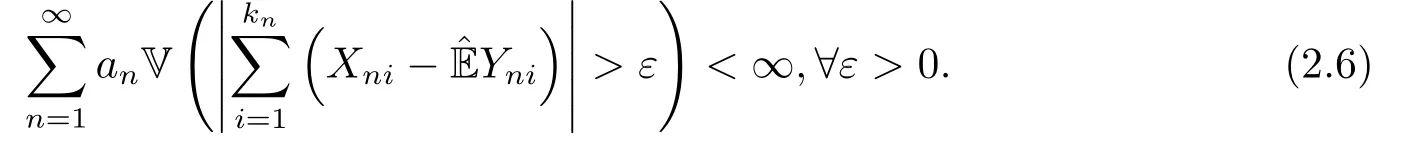
注定理2.1是将文[18]中定理3.1的结论从概率空间推广到了次线性期望空间,并推广得到更一般的结果.文[20]的定理3.2虽然也是将文[18]中定理3.1的结论推广到次线性期望空间,但是它的期望定义与本文不同,所以得到的结论与本文的结论互不包含.
证由(2.1)可知

所以要证明(2.4)式,只需证
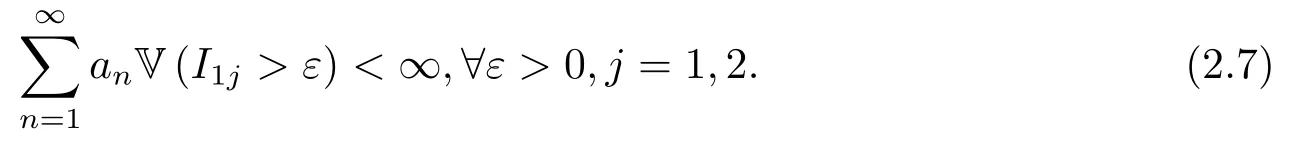
首先将所有自然数分为如下A11和A12两个数集:

由A12的定义和(2.3)式很容易可以得到

因此,只需证明

首先证明j =1时的(2.8)式.由(2.2)式就有
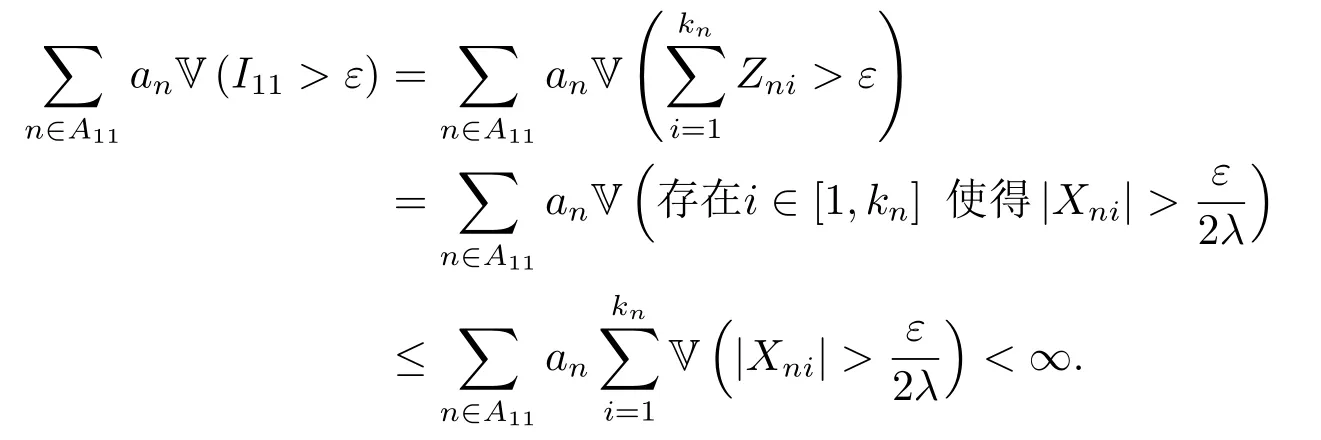
再证明j =2时的(2.8)式.下面分为三种情况来证明.
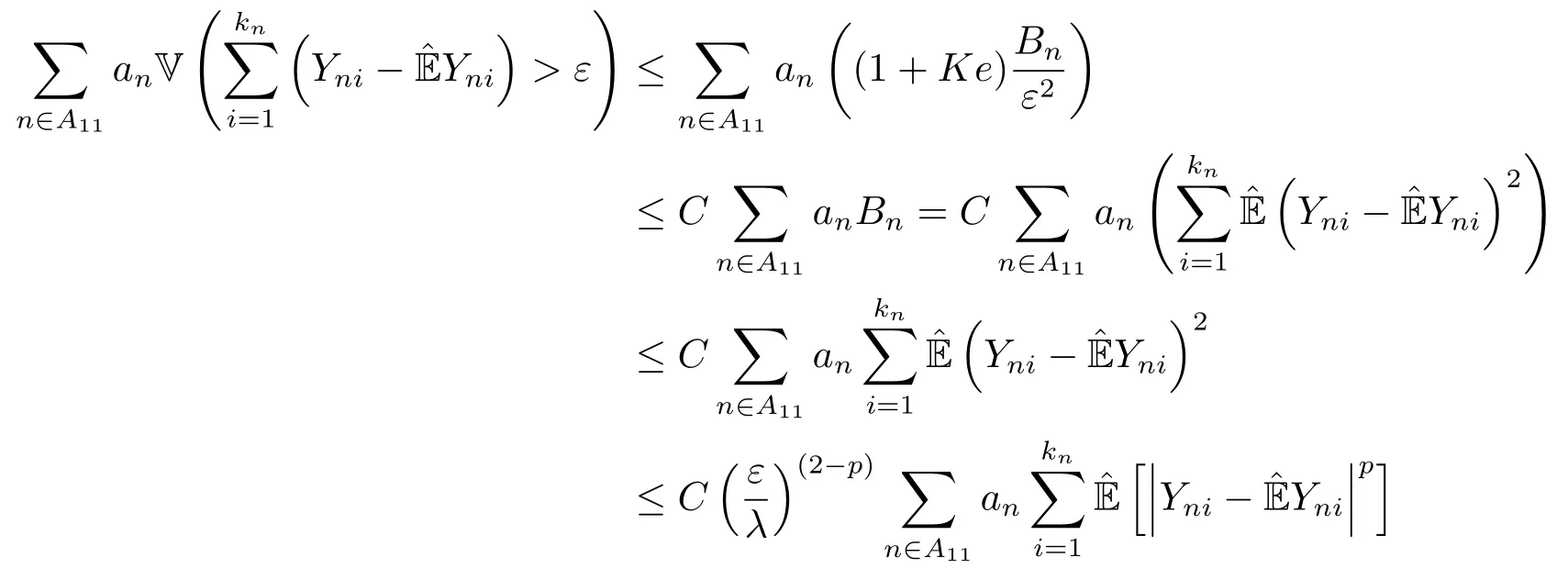

由此便完成了在0 <p ≤2和0 <λ ≤1条件下的(2.4)式的证明.
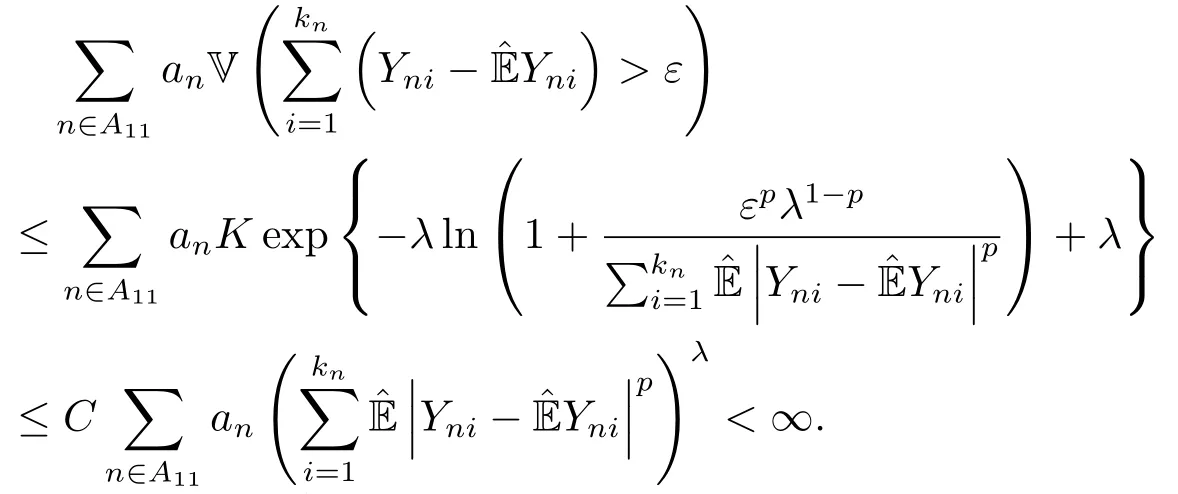
由此完成了在0 <p ≤2和λ >1条件下的(2.4)式的证明.
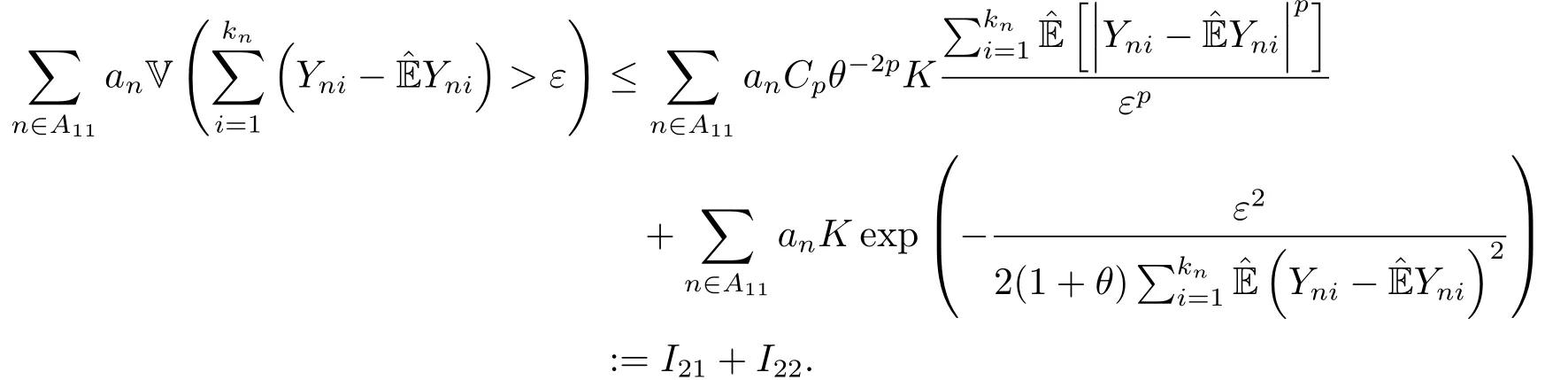
所以要证明j = 2时的(2.8)式,只需证明I21<∞和I22<∞.首先证明I21<∞.由0 <λ ≤1和(2.3)式可得

再证明I22<∞.由当x >0时和(2.3)式可得

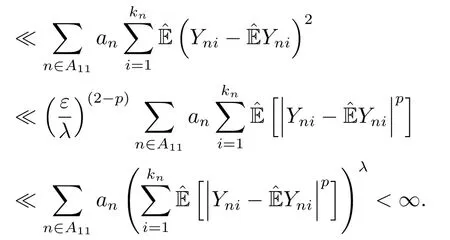
由此就得到了在p >2和0 <λ ≤1条件下的(2.4)式.
结合1),2)和3)便完成了(2.4)的证明.

因此有

这样就得到了(2.5)式.

这便得到式子(2.6),即完成了定理2.1的证明.
猜你喜欢
杂志排行
应用数学的其它文章
- New Iteration Method for a Quadratic Matrix Equation Associated with an M-Matrix
- 具有随机保费和交易费用的最优投资-再保险策略
- 带有N策略的不可靠重试队列的均衡策略分析
- A Smoothing Newton Algorithm for Tensor Complementarity Problem Based on the Modulus-Based Reformulation
- The Center Problems and Time-Reversibility with Respect to a Linear Involution
- Boundary Value and Initial Value Problems with Impulsive Terms for Nonlinear Conformable Fractional Differential Equations
