改编常规习题 撬动思维发展——《长方形和正方形周长复习》练习设计与教学实施

俞国芳

复习课，不是习题的堆砌，也不是简单的重复。教师应选择有利于学生思维投入的练习，让复习课也具有生长的力量。练习设计并非要另辟蹊径，教材中的常规习题蕴藏着丰富的学习资源，充分挖掘、合理利用常规习题是有发展力的学习素材。笔者以《长方形和正方形周长的复习》为例，谈一谈如何改编常规习题，培养学生能力。

一、改变数据，从少到多，培养思维的发散性

《长方形和正方形》是人教版第五册第七单元的学习内容，是学习平面图形的基础，重在理解周长的意义。教材配套作业本（浙江教育出版社）中有如下练习：“两个长8 厘米、宽4 厘米的长方形可以拼成怎样的图形？这个图形的周长是多少厘米？”学生可以得出如下结论：

解答：（8×2+4）×2=40（厘米）

解答：（8+4×2）×2=32（厘米）

解答：（8+8+4）×2=40（厘米）

练习课中的重点是关注长方形周长的计算，而复习课不仅需要巩固周长的计算，还要拓展学生的解题思路、多角度地考虑问题，使学习更深入。

【改编】三个长是8 厘米、宽是4 厘米的长方形可以拼成怎样的图形？ 周长是多少？

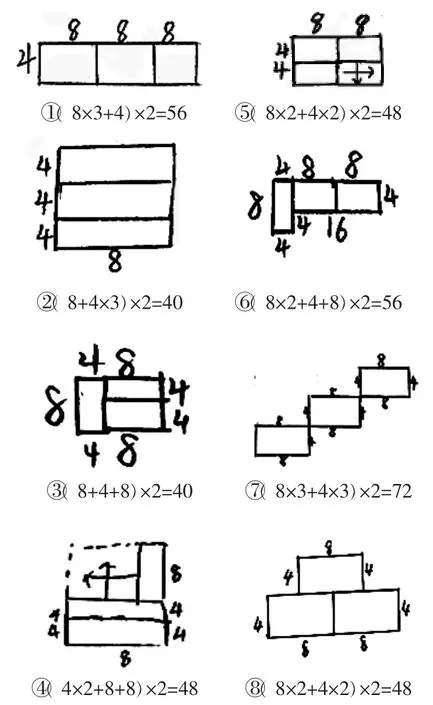
三个长方形可以拼出更多不同的图形，通过数据的改变，将习题变得更为开放。从解答情况反映出学生思维层次与学习态度的不同。全班11%的学生写出2 种拼法，有68%的学生能写出3 种拼法，有21%的学生写出了4 种及以上拼法。

师：拼成的图形形状不同，为什么有些图形的周长相同？

生：②③这两个图形重叠的边都是长边，所以周长都比3 个分开的长方形少了4 个8 厘米。

生：两个图形重叠部分相同，周长也会减少相同的部分，所以周长相同。

师：三个长方形怎样拼周长最长？怎样拼周长最短？

生：图形之间重叠的部分越多，周长越短；重叠部分越少，周长越长。

数据的改变增加了图形拼组的情况，学生不仅巩固了周长的计算、平移知识，还从相同的答案中发现周长不变的原因，得出了拼组后图形周长的多种计算方法。学生的知识得到巩固，思维得到了发散。

二、拓展认知，从特殊到一般，培养思维的深刻性

当学生遇到有分歧的观点，或得到的结果与自己当前的理解有差异时，就会产生认知冲突。认知冲突的解决会让学生学到新的知识，提高理解水平。课本88 页有如下练习：

下图的长方形分成两个部分，哪个部分的周长长？

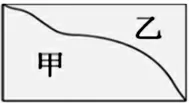
90%的学生第一感觉认为两个图形的周长不同，教师引导学生思考图形的周长，描一描图形的边线，学生发现两部分图形有一条公共边，是两条相等的边，所以图形的周长相等。学生在此基础上，还设计出很多周长相等的两部分。

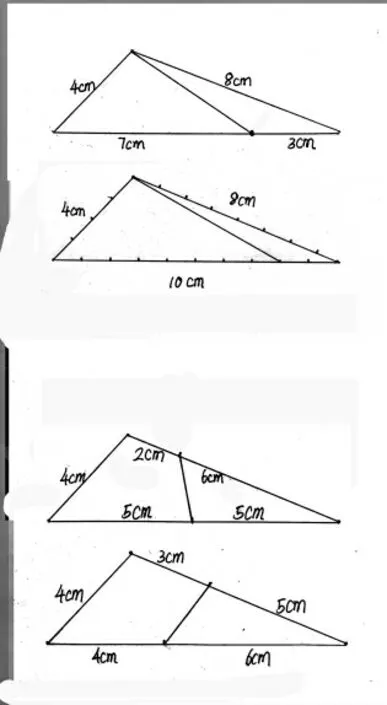
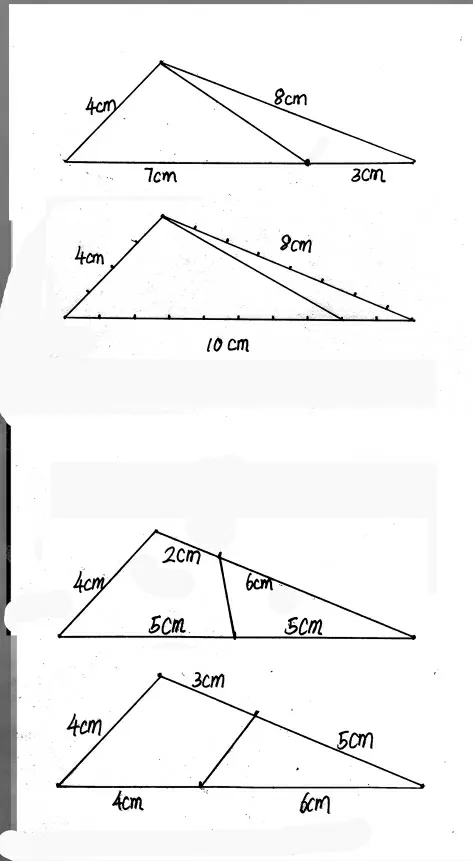
为使学生对周长的理解更到位，认识更深入，笔者在复习课上将长方形改成三角形，将特殊图形改成一般图形，检验学生对周长比较的认识。【改编】将下图的三角形分成两个周长相等的图形。

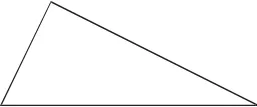
受已有知识和经验的负迁移，全班有89.2%学生将三角形一条边对分，如图①、图②、图③；21.6%的学生认为三角形的边有长短，分成两个底边长短不一的三角形，如图④、图⑤；仅10.2%的学生量出三角形三条边的长度，将三角形分成了周长相等的两部分，如图⑥。

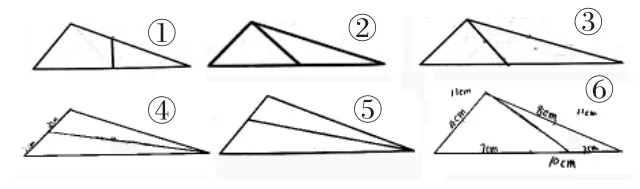
教师引导学生对比思考图①、图②、图③。

师：你是怎么分的？周长相等吗？

生：长方形的中点连一连，分成的两部分周长是相等的。我找到一条边的中点连起来，作为一条公共边，这样三角形的两部分也相等。

生：周长相等的两部分除公共边外，另外的几条边也要相等，图①、图②、图③的两个图形的边是不相等的。

教师引导学生对比思考图②、图⑤、图⑥的周长，明白要使图形周长相等，必须要所有边的长度总和相等。学生意识到不能像图⑤这样随意画，需要量出三角形三条边的长度。

师：知道三条边的长度该怎样连线才能将三角形分成两个周长相等的图形？

生：除了公共边，我们也要想办法让剩下的边长度相等。

生：三角形三条边长度不同，我把它平均分成两部分，再连线，就可以得出周长相等的图形了。

分成两个周长相等的三角形：

分成两个周长相等的图形：

认识事物总是从特殊到一般，从而发现事物的本质属性，发现事物存在的普遍规律。通过练习，进一步使学生明白两部分周长相等需要所有的边相等，与正方形、长方形分成周长相等的两部分本质上是相同的，沟通了方法上的联系，真正从概念的本质理解问题、解决问题。

三、打破惯性，从常规到非常规，培养思维的灵活性

史宁中教授说：“创新能力来自知识积累、经验积累和思维训练。”长方形周长在生活中应用广泛，教师有意识地选择生活与数学相联系的练习，帮助学生巩固知识技能，增强实际应用能力。

例：一块长方形菜地，长6米，宽3 米。四周围上篱笆，篱笆长多少米？如果一面靠墙，篱笆至少要多少米？

这是教材第88 页的练习，意在巩固周长的计算，能运用周长的知识解决实际生活问题。将菜地一面靠墙，这是生活中常见的方法，可以节约材料。学生在解决问题时提出两种可能：长边靠墙：6+3×2=12（米）；短边靠墙：6×2+3=15（米），通过图示表达，也比较容易解决。复习课上，我们将这一材料加以改编，在此基础上提出新的问题：

【改编】养鸡专业户李伯伯要新建一座长方形鸡舍，鸡舍长23米，宽15 米。

（1）建这个鸡舍需要多少米的材料？

（2）李伯伯为了节约材料，想靠墙建鸡舍，墙长20 米。要怎样建最好？ 此时篱笆的周长是多少米？（画图分析并计算）

第一个问题是基础，学生利用长方形周长的计算方法可以得出建鸡舍需要（23+15）×2=76（米）。第二个问题改变原有教材表述（教材习题没有说明墙的长度），给予的信息是墙只有20 米，给解决问题设置了限定。

解一：（20+15）×2=70（米）。

生：这道题我做错了，我想着墙只有20 米，鸡舍也只能建20米长。但我计算了周长后忘记减去利用墙做篱笆的那段长度。（比例：5.4%）

解二：23+15+15=53（米）。

生：鸡舍靠墙建设比较节约材料，可以长边靠墙，也可以短边靠墙，所以我就选了长边靠墙更节约。但是没有考虑到墙只有20米。（比例：2.7%）

解三：2×23+15=61（米）。

生：墙只有20 米，李伯伯要建长23 米的鸡舍，长的一边靠墙不够，所以就用短的一边靠墙，这样周长最短。（比例：81.1%）

解四：15×2+23+3=56（米）。

生：墙20 米，鸡舍的长要23米，是不够长的，如果把短边靠墙，可以节约15 米的材料，如果长边靠墙，可以节约23 米。虽然不够，我补3 米，这样还是比短边靠墙要节约。（比例：10.8%）

81.1%的学生认为长边靠墙不够，就只能短边靠墙，只有10.8%的学生想到只要补上长边不够的那部分篱笆，也可以利用墙的长度来建设鸡舍。特殊的设计方法给学生“豁然开放”的感觉。

练习的改编设计，使思维敏捷、有开拓精神的学生找到了展示的舞台。经过方法讨论，让其他学生打破了原有的固定思维，形成新的思考方式，也获得了更优化的解决问题的途径和方法。这是学生在今后学习和生活中的一种创新能力的需要，通过习题的设计可以逐步培养学生“逆向思维、非常规思维”，提高学生解决问题的能力。

不同的学生能力有差异，复习课不仅巩固了知识还提升了学生综合能力。教师在选择练习材料时，需要充分考虑不同层次学生的发展需要，在能力要求、解决策略、思维表达上都能有梯度的设计，让不同的学生有不同的发展。