考虑指定性能的有限时间制导控制一体化设计

宋海涛 王仕成 姚二亮

摘 要：针对拦截弹控制通道耦合的制导控制一体化问题， 提出基于有限时间观测器和指定性能控制的设计方法。 该方法利用有限时间观测器处理系统不确定性， 对其进行精确快速估计， 提高系統实时性。 然后， 基于指定性能控制思想， 采用动态面控制的设计步骤， 确保实现非匹配级联系统的指定性能控制目标。 通过分析算法的稳定性， 获得控制器的参数取值范围。 最后， 利用仿真实例进行验证， 所设计的方法对来袭目标实现准确有效拦截， 并确保拦截过程的指定性能要求。

关键词：     拦截弹; 制导控制一体化; 指定性能; 有限时间观测器; 不确定性

中图分类号：     TJ765; V448   文献标识码：    A  文章编号：     1673-5048（2021）06-0028-06

0 引  言

制导控制一体化（Integrated Guidance and Control，  IGC）是飞行器飞行控制技术发展的一个新趋势， 为应对新型突防技术的挑战提供了强有力的技术支撑[1]。 该技术将制导子系统与姿控子系统看作一个整体， 提高两部分的协调匹配程度， 从而提升飞行器的控制品质[2]。 相比传统的制导控制技术， 制导控制一体化具有以下优点： （1）从功能上， 直接实现目标截获， 结构简单; （2）从本质上， 制导控制一体化将飞行器动力学融入制导设计， 解决了传统分离设计的频率界限要求; （3）从控制器设计上， 单个闭环的设计要比传统双闭环的设计更方便。 因此， 制导控制一体化代表着飞行器飞行控制技术的发展趋势。

当前， 对制导控制一体化的研究， 已经由问题描述阶段过渡到控制器设计及应用研究阶段， 主要集中在研究制导控制一体化的鲁棒性、 精确性、 快速性、 约束条件等方面。 制导控制一体化控制器性能直接决定飞行器的飞行控制能力。 文献[3]利用反演滑模控制对俯仰平面内制导控制一体化问题进行研究， 算法具有较强的鲁棒性。 文献[4]针对直接力/气动力复合控制导弹的制导控制一体化问题， 采用自适应反演滑模控制设计方法， 利用控制分配将期望控制量映射到直接力装置和升降舵面。 文献[5]得到集成度高、 系统阶数低的制导控制一体化模型， 将制导控制问题转化为非线性系统输出调节问题， 提高了控制方法的鲁棒性。 文献[6]利用非线性干扰观测器对不确定性的界进行估计， 提高拦截精确性和鲁棒性。 文献[7]使用自抗扰控制技术设计了制导控制一体化系统， 具有较好的动态特性和鲁棒性。 文献[8]提出一种考虑输入饱和约束的制导控制一体化设计方法， 实现系统状态全局有限时间稳定。 文献[9]设计三维耦合的快速鲁棒制导控制一体化控制器， 构建非奇异终端滑模面， 控制器快速性大大提高。 其中快速性是飞行器的关键性能指标， 尤其对于高速率、 大机动场合。 文献[10]利用高阶滑模微分器估计一体化模型中目标的加速度， 利用神经网络逼近导弹的不确定性， 具有较好的实时性。 文献[11]提出快速全局收敛的制导控制一体化技术， 提供系统全局收敛时间的解析表达式， 有利于优化系统的快速性。

为了提升制导控制一体化的飞行控制能力， 可通过调整飞行过程的动态性能和稳态性能实现。 基于指定性能控制设计制导控制一体化控制器， 使跟踪误差收敛到一个预定义的无限小集合内， 且收敛速度低于某值， 从而提升跟踪精度、 反应速度。

本文主要从制导控制一体化的性能角度开展研究， 对模型中存在的非匹配不确定项，  利用有限时间观测器对其取值进行准确快速估计。 对于拦截跟踪系统， 引入性能指标函数的非线性变换， 基于动态面步骤， 设计指定性能的控制器。 通过系统稳定性分析， 得到控制器参数的取值范围。 最后， 通过仿真实例验证本文所提方法的有效性。

1 研究对象

在三维空间中， 拦截弹—目标的相对运动关系如图1所示。 图中，  oxyz为参考惯性坐标系; ox1y1z1为视线坐标系; o表示拦截弹质心; T表示目标质心; ε， η分别是弹目视线倾角、 弹目视线偏角。

为了便于进行控制器设计， 将全维制导控制一体化模型分别投影在三个独立通道上。 根据文献[12]， 得到考虑拦截弹通道之间耦合因素的三通道制导控制一体化模型。

1.1 俯仰通道

俯仰通道的制导控制一体化模型如下：

x·=a11a1200a2210a320x+00b3u+d1d2d3y=x1 （1）

式中： x=ε·αωzT， ε·是弹目视线倾角速率， α是攻角， ωz是弹体转动角速率; u=δz， δz是拦截弹俯仰通道的等效舵偏角; y=ε·; a11=-2R·R， R是弹目相对距离; a12=-P+qScαymR， P是拦截弹发动机推力， q是动压， S是拦截弹参考面积， m是弹体质量; a22=-qScαy+PmV， V是拦截弹速度; a32=qSLmαzJz， L是拦截弹参考长度， Jz是拦截弹转动惯量; b3=qSLmδzzJz; cαy， mαz， mδzz是拦截弹空气动力参数; 不确定项d1， d2， d3包括三通道之间的耦合因素、 拦截弹重力分量、 气动参数摄动、 外界扰动、 线性化近似误差等。

1.2 偏航通道

偏航通道具有与俯仰通道结构类似的制导控制一体化模型：

x·=a11a1200a2210a320x+00b3u+d1d2d3y=x1  （2）

式中： x=η·βωyT， η·是弹目视线偏角速率， β是侧滑角， ωy是弹体转动角速率; u=δy， δy是拦截弹偏航通道的等效舵偏角; y=η·; a11=-2r·r， r是弹目相对距离; a12=qScβz-Pmr; a22=qScβz-PmV; a32=qSLmβyJy， Jy是拦截弹转动惯量; b3=qSLmδyyJy; cβz， mβy， mδyy是拦截弹空气动力参数。

1.3 滚动通道

滚动通道的制导控制一体化模型如下：

x·=0100x+0b2u+d1d2y=x1 （3）

式中： x=γωxT， γ是滚动角， ωx是弹体转动角速率; u=δx， δx是拦截弹滚动通道的等效舵偏角; y=γ; b2=qSLmδxxJx， Jx是拦截弹转动惯量， mδxx是拦截弹空气动力参数。

制导控制一体化控制器设计的目的： 根据拦截的平行接近法思想， 选择合适的控制量， 使视线角速率ε·， η·尽快趋于零值， 同时维持一定的滚动角， 并使控制的动态过程满足动态性能和稳态性能要求。

以俯仰通道为例， 设计制导控制一体化控制器并对其进行性能分析。

2 控制器设计

俯仰通道制导控制一体化模型式（1）可写为

x·=f（x）+g（x）u+dy=100x  （4）

式中： f（x）=a11x1+a12x2a22x2+x3a32x2;g（x）=00b3;d=d1d2d3。

控制器的设计分为两部分： 有限时间观测器对制导控制一体化模型中的不确定项进行估计; 指定性能控制器提供控制量实现制导控制一体化系统的控制目标。

2.1 有限时间观测器

模型式（4）中的不确定项d未知， 为了抵消其对控制器的影响， 利用有限时间干扰观测器方法对d进行估计[13]， 使估计值有限时间收敛到真值。

假设系统式（4）中非匹配等价不确定项d1， d2， d3一阶连续可微， 且其一阶导数分别具有Lipschitz常数L1， L2， L3。

系统的干扰观测器如下：

w·0=v0+f（x）+g（x）u

w·1=v1

v0， n=w1， n-λ0L13nw0， n-xn23sgnw0， n-xn

v1， n=w2， n-λ1L12nw1， n-v0， n12sgnw1， n-v0， n

w·2， n=-λ2Lnsgnw2， n-v1， n （5）

式中： n=1， 2， 3; x=x1x2x3T; w0=w0， 1w0， 2w0， 3T;  w1=w1， 1w1， 2w1， 3T; w2=w2， 1w2， 2w2， 3T; v0=v0， 1v0， 2v0， 3T; v1=v1， 1v1， 2v1， 3T; λ0， λ1， λ2是待設计的观测器参数， 对于本系统， 选择λ0=8， λ1=5， λ2=5。 该干扰观测器有限时间收敛， 即在有限时间内可实现对系统状态及不确定项的估计： x^=w0， d^=w1， d·^=w2。

2.2 指定性能制导控制一体化控制器

利用有限时间观测器得到的不确定项估计值代替真实值， 得到如下模型：

x·1=a11x1+a12x2+d^1x·2=a22x2+x3+d^2x·3=a32x2+b3u+d^3  （6）

为了对拦截过程的动态性能和稳态性能进行控制， 可通过约束系统输出即弹目视线角速率ε·进行体现。 以下基于指定性能控制设计控制器。

指定性能控制利用指定性能函数和误差转换， 使跟踪误差e（t）=x1（t）-xd（t）收敛到一个预定义的无限小的集合内， 且收敛速度低于指定值、 超调量低于指定值[14]。 而制导控制一体化系统中， xd（t）=0。

选择性能函数[15-16] 如下：

ρ（t）=ρ0-ρ∞e-lt+ρ∞（7）

e（t）满足如下条件， 可确保控制目标：

-δρ（t）<e（t）<ρ（t）  e（0）≥0-ρ（t）<e（t）<δρ（t）  e（0）<0  （8）

式中：

ρ∞表示跟踪误差e（t）的稳态最大允许幅值; ρ（t）的衰减速度e-lt成为e（t）期望收敛速度的下界， 最大超调量小于δρ（0）， 可通过设置δ=0而使最大超调量为零。 因此， 性能函数ρ（t）和设计常数δ的合理选择可体现系统输出轨迹的行为界限。

为了将控制器的两个目的统一起来， 进行误差转换， 将原始的具有跟踪误差行为约束的非线性系统转换为一个等价无约束系统。

误差转换式定义如下：

z1=S-1e（t）ρ（t）=lne（t）ρ（t）-M-e（t）ρ（t）（9）

式中： e（t）=ρ（t）S（z1）; z1为转换的误差;  S（·）为平滑、 严格递增且可逆函数， 且M<S（z1）<。

对式（9）进行微分求导， 得

z·1=S-1e（t）ρ（t）e（t）ρ（t）′=r[a11x1+a12x2+d1-v]（10）

式中： r=S-1e（t）ρ（t）1ρ（t）;   v=x·d（t）+e（t）（t）ρ（t）。 r， v包含与跟踪系统特性相关的因素， 这些因素已知且包含在系统设计之中。 由于误差转换的性质， 只要满足z1（t）∈L∞， 则r>0， r， v有界。

原系统可转换为

z·1=-vr+ra11x1+ra12x2+rd^1=

-vr+ra11x1+ra12x2+Δz1x·2=a22x2+x3+d^2x·3=a32x2+b3u+d^3 （11）

所以， 设计控制器， 使z1有界， 就可确保实现控制目标， 且z1的界限并不影响e（t）的变化。

定理： 对于系统式（6）， 利用性能函数式（7）和输出误差转换式（9）， 引入系统跟踪误差的动态和稳态性能需求， 则转换系统式（11）的状态稳定有界， 可确保原系统式（6）的指定性能跟踪误差[17-19]。

定义第一个动态面：

s1=z1（12）

对s1求导：

s·1=z·1=-vr+ra11x1+ra12x2+Δz1（13）

为使s1有界， 选择虚拟控制输入：

x2， c=-1ra12k1s1+va12-a11a12x1-1ra12Δz1（14）

式中： k1>0。

由式（13）～（14）可得

s·1=-k1s1（15）

为了避免反演法中对中间虚拟变量x2， c的直接微分， 设计一阶动态滤波器， 将x2， c通过一阶动态滤波器来代替x2， d， x2， d为滤波器的输出， 有

τ1x·2， d+x2， d=x2， c，  x2， d（0）=x2， c（0）（16）

式中： τ1为滤波器时间常数。

定义第二个动态面：

s2=x2-x2， d （17）

选择x3， d而促使s2→0。

对s2求导：

s·2=x·2-x·2， d=a22x2+x3+d^2-x·2， d （18）

构造虚拟控制量：

x3， c=-k2s2-a22x2+x·2， d-d^2（19）

式中： k2为正常數。

由式（18）～（19）， 可得

s·2=-k2s2（20）

将x3， c通过一阶动态滤波器代替x3， d。 x3， d为滤波器的输出， 有

τ2x·3， d+x3， d=x3， c， x3， d（0）=x3， c（0）（21）

式中： τ2为滤波器时间常数。

定义第三个动态面：

s3=x3-x3， d（22）

选择u而促使s3→0。

对s3求导：

s·3=x·3-x·3， d=a32x2+b3u+d^3-x·3， d（23）

同理， 选择虚拟控制输入：

u=-k3b3s3-a32b3x2+x·3， db3-d^3b3（24）

由式（23）～ （24）， 可得

s·3=-k3s3 （25）

3 性能分析

一阶动态滤波器的误差：

ρi=xi+1， d-xi+1， c，  i=1， 2（26）

求导， 得

ρ·i=x·i+1， d-x·i+1， c=xi+1， c-xi+1， dτi-x·i+1， c=

-ρiτi-x·i+1， c （27）

由x2， c， x3， c可知， 其导数存在并且有界， 即存在δx·， 使

x·i+1， c≤δx·（28）

设

Vρi=12ρ2i （29）

求导， 得

V·ρi=ρii=-ρiρiτi+x·i+1， c=-2Vρiτi-ρix·i+1， c≤

-2Vρiτi+12ρ2i+δ2x·=-2τi-1Vρi+12δ2x· （30）

状态跟踪误差即为定义的动态面变量， 其导数为式（15）， （20）， （25）， 取

VS=12∑3i=1s2i（31）

求导， 得

V·S=12∑3i=1s2i=s1s·1+s2s·2+s3s·3=s1-k1s1+s2-k2s2+s3-k3s3=-k1s21-k2s22-k3s23（32）

为了分析系统稳定性， 定义李雅普诺夫函数：

V=∑2i=1Vρi+VS（33）

求导， 得

V·=∑2i=1V·ρi+V·S≤-2τ1-1Vρ1-2τ2-1Vρ2+

δ2x·-k1s21-k2s22-k3s23 （34）

取=min2τ1-1， 2τ2-1， 2k1， 2k2， 2k3=δ2x· ， 则

V·≤-V+（35）

令2τ1-1， 2τ2-1， 2k1， 2k2， 2k3>0， 推导得

τ1， τ2<2k1， k2， k3>0 （36）

当控制器参数满足以上条件时， 则V（t）≤V≡maxV（0）， ， 系统所有信号有界， 分别位于集合ρi=ρi∈R：ρi≤2V， i=i∈R：i≤2V， Si=Si∈R：Si≤2V内。 由S1=z1有界， 则根据指定性能控制性质， 可知其满足性能要求。

综上， 只要控制器参数满足条件， 而不需要选择参数的极限值使集合ρi， i， Si无限小， 就可满足系统动态及稳态性能需求。 因此， 对于满足假设条件的任意不确定性， 控制器都可以抵消其影响， 提高系统的鲁棒性。

同法， 对于滚动通道， 可得类似结果。

4 仿真验证

本部分通过实验仿真检验所设计算法的有效性。 拦截场景为： 单枚拦截弹拦截来袭目标， 假定来袭目标的运动状态信息可测可得。 拦截弹位置、 速度变量的初始值为xM（0）=[0200300]T m， VM（0）=600 m/s， 来袭目标的位置、 速度变量的初始值为xT（0）=[7 0001 000500]T m， VT（0）=200 m/s， 假设目标速度为常值， 拦截弹的初始速度方向平行于初始弹目视线方向。 拦截弹相关参数设置参见文献[12]。

控制器参数选择如下： k1=0.008， k2=0.008， k3=0.008， τ1=1， τ2=1，  L1=L2=L3=100。 假设目标机动过载为nTy（0）=5， nTz（0）=5， 设稳态误差为ρ∞=0.001， 最小收敛速度为e-lt=e-0.1t， 超调度δ=0.1， 设置初始值ρ0=1， 则所对相应的性能函数为ρ（t）=0.999e-0.1t+0.001。

图2～3给出对应的弹目视线倾角速率、 偏角速率仿真曲线。 由图可见， 算法对应的视线角速率曲线与性能函数满足式（8）。 因此， 弹目视线倾角速率、 偏角速率的跟踪稳态误差小于ρ∞=0.001、 收敛速度高于e-0.1t。

在仿真中， 选择拦截弹的盲区半径为30 m， 拦截轨迹如图4。 拦截时间为21.509 s， 脱靶量为29.980 1 m。 最终的控制量， 即舵偏角信号如图5所示。

控制算法中的动态控制面变量s1， s2， s3变化曲线如图6所示， 可见动态控制面变量有界， 根据指定性能控制方法特点， 系统原状态弹目视线倾角速率、 偏角速率x1必然满足指定性能要求。

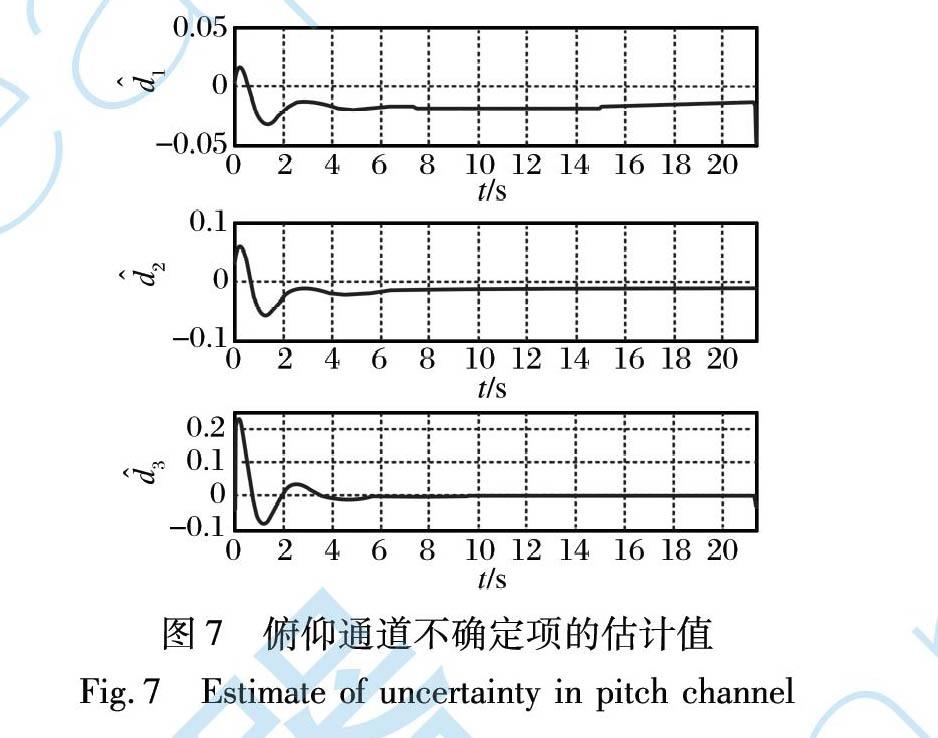
有限时间观测器对模型中的不确定项进行估计， 以俯仰通道为例， 不确定项d1， d2， d3的估计值d^1， d^2， d^3如图7所示。 由估计值曲线可知， 有限时间观测器大约在6 s收敛到恒定值。

5 结  论

本文从拦截弹的飞行控制性能角度研究制导控制一体化的设计问题。 针对制导控制一体化中的不确定项， 利用有限时间观测器对其进行精确估计; 根据拦截性能需求， 设定性能函数， 利用指定性能控制进行跟踪误差转换， 利用转换状态的有界性确保原系统状态的动态特性和稳态特性; 动态面控制的設计步骤解决了非匹配不确定项的问题。 仿真结果验证了本文方法的有效性。

参考文献：

[1] 宋海涛，  张涛，  张国良. 飞行器制导控制一体化技术[M]. 北京： 国防工业出版社，  2017.

Song Haitao，  Zhang Tao，  Zhang Guoliang. Integrated Guidance and Control Technology for Aircraft[M]. Beijing： National Defense Industry Press，  2017.（in Chinese）

[2] 田栢苓，  李智禹，  吴思元，  等. 可重复使用运载器再入轨迹与制导控制方法综述[J]. 航空学报，  2020，  41（11）： 624072.

Tian Bailing，  Li Zhiyu，  Wu Siyuan，  et al. Reentry Trajectory Optimization，  Guidance and Control Methods for Reusable Launch Vehicles： Review[J]. Acta Aeronautica et Astronautica Sinica，  2020，  41（11）： 624072.（in Chinese）

[3] 齐辉，  张泽，  韩鹏鑫，  等. 基于反演滑模控制的导弹制导控制一体化设计[J]. 系统工程与电子技术，  2016，  38（3）： 618-623.

Qi Hui，  Zhang Ze，  Han Pengxin，  et al. Integrated Design of Missile Guidance and Control Based on Back-Stepping and Sliding Mode Control[J]. Systems Engineering and Electronics，  2016，  38（3）： 618-623.（in Chinese）

[4] 李雨涛，  李爱军，  张金鹏，  等. 基于控制分配的复合控制导弹制导控制一体化设计[J]. 航空兵器，  2018（6）： 32-38.

Li Yutao，  Li Aijun，  Zhang Jinpeng，  et al. Integrated Guidance and Control Design for Blended Control Missile Based on Control Allocation[J]. Aero Weaponry，  2018（6）： 32-38.（in Chinese）

[5] 王建华，  刘鲁华，  王鹏，  等. 高超声速飞行器俯冲段制导控制一体化设计方法[J]. 航空学报，  2017，  38（3）： 320328.

Wang Jianhua，  Liu Luhua，  Wang Peng，  et al. Integrated Guidance and Control Scheme for Hypersonic Vehicles in Dive Phase[J]. Acta Aeronautica et Astronautica Sinica，  2017，  38（3）： 320328.（in Chinese）

[6] He S M，  Wang W，  Wang J. Three-Dimensional Multivariable Integrated Guidance and Control Design for Maneuvering Targets Interception[J]. Journal of the Franklin Institute，  2016，  353（16）： 4330-4350.

[7] 趙坤，  曹登庆，  黄文虎. 突防导弹机动、 制导与控制一体化设计[J]. 系统工程与电子技术，  2018，  40（9）： 2040-2047.

Zhao Kun，  Cao Dengqing，  Huang Wenhu. Integrated Design of Maneuver，  Guidance and Control for Penetration Missile[J]. Systems Engineering and Electronics，  2018，  40（9）： 2040-2047.（in Chinese）

[8] 王松艳，  孙向宇，  杨胜江，  等. 考虑输入饱和的制导控制一体化设计[J]. 航空学报，  2017，  38（10）： 320897.

Wang Songyan，  Sun Xiangyu，  Yang Shengjiang，  et al. Integrated Guidance and Control Design Considering Input Saturation[J]. Acta Aeronautica et Astronautica Sinica，  2017，  38（10）： 320897.（in Chinese）

[9] Song H T，  Zhang T. Fast Robust Integrated Guidance and Control Design of Interceptors[J]. IEEE Transactions on Control Systems Technology，  2016，  24（1）： 349-356.

[10] 周觐，  雷虎民，  李炯，  等. 基于神经网络的导弹制导控制一体化反演设计[J]. 航空学报，  2015，  36（5）： 1661-1672.

Zhou Jin，  Lei Humin，  Li Jiong，  et al. Integrated Missile Gui-dance and Control Design Based on Neural Network and Back-Stepping Control Theory[J]. Acta Aeronautica et Astronautica Sinica，  2015，  36（5）： 1661-1672.（in Chinese）

[11] Song H T，  Zhang T. Fast Integrated Guidance and Control with Global Convergence[J]. Journal of Central South University，  2019，  26（3）： 632-639.

[12] Song H T，  Zhang T，  Zhang G L，  et al. Integrated Interceptor Guidance and Control with Prescribed Performance[J]. International Journal of Robust and Nonlinear Control，  2015，  25（16）： 3179-3194.

[13] Yang J，  Li S H，  Su J Y，  et al. Continuous Nonsingular Terminal Sliding Mode Control for Systems with Mismatched Disturbances[J]. Automatica，  2013，  49（7）： 2287-2291.

[14] Bechlioulis C P，  Rovithakis G A. Adaptive Control with Guaranteed Transient and Steady State Tracking Error Bounds for Strict Feedback Systems[J]. Automatica，  2009，  45（2）： 532-538.

[15] Shojaei K，  Kazemy A. Adaptive Neural Feedback Linearizing Control of Type （m，  s） Mobile Manipulators with a Guaranteed Prescribed Performance[J]. Robotica，  2019，  37（11）： 1937-1955.

[16] Jing Y H，  Yang G H. Adaptive Quantized Tracking Control for a Class of Uncertain Nonlinear Systems with Guaranteed Transient Performance[J]. Journal of the Franklin Institute，  2018，  355（13）： 5414-5430.

[17] Wang W，  Wen C Y. Adaptive Actuator Failure Compensation Control of Uncertain Nonlinear Systems with Guaranteed Transient Performance[J]. Automatica，  2010，  46（12）： 2082-2091.

[18] Kostarigka A K，  Doulgeri Z，  Rovithakis G A. Prescribed Perfor-mance Tracking for Flexible Joint Robots with Unknown Dynamics and Variable Elasticity[J]. Automatica，  2013，  49（5）： 1137-1147.

[19] Yoo S J. Fault-Tolerant Control of Strict-Feedback Non-Linear Time-Delay Systems with Prescribed Performance[J]. IET Control Theory & Applications，  2013，  7（11）： 1553-1561.

Integrated Guidance and Control  Design Considering

Prescribed Performance and Finite Time

Song Haitao*， Wang Shicheng， Yao Erliang

（The Rocket Force University of Engineering，  Xi’an 710025，  China）

Abstract： Aiming at the integrated  guidance and control  of interceptor considering the couplings among control channels，  a design method based on finite time observer and prescribed performance control is proposed. The finite time observer is used to deal with the system uncertainties，  which are estimated accurately and fastly to improve the real-time performance of system. Based on the prescribed performance control，  the design steps of dynamic surface control are presented to guarantee the prescribed performance control of this mismatched cascade system. The ranges of parameters are obtained by the stability analysis of algorithm. The simulation results verify that the designed method can intercept the incoming target accurately and effectively，  and can guarantee the prescribed performance requirements in the interception process.

Key words：  interceptor; integrated guidance and control; prescribed performance; finite time observer; uncertainty