基于弹道超实时仿真的多弹协同制导研究
2021-01-06张鹏鲁浩沈欣
张鹏 鲁浩 沈欣







摘 要:在导弹速度不可控的情况下进行多弹时间协同制导具有很大难度。 弹道实时仿真方法能准确估计剩余飞行时间, 并预测弹道信息。 基于此, 本文建立了水平面控制过载与各导弹飞行时间误差之间的闭环控制, 进而使所有导弹的飞行时间趋于一致, 实现攻击时间协同, 另外设计了具有攻击角度约束的弹道成型制导律。 对设计的制导律进行六自由度仿真验证, 结果表明, 以弹道超实时仿真为基础设计的多弹协同制导律能够保证多枚导弹同时以期望的攻击角度命中目标。
关键词: 协同制导律; 攻击时间约束; 攻击角度约束; 超实时仿真; 剩余飞行时间; 多弹协同
中图分类号: TJ765; V448 文献标识码: A 文章编号: 1673-5048(2021)06-0034-06
0 引 言
1997年, 美国提出了“网络中心战”作战体系, 经过不断的完善, 正在朝着“分布式作战”、 “决策中心战”等新的方向转变。 可以预见, 未来战争将是体系与体系的对抗, 战争形态也必将呈现信息化、 电子化、 网络化、 智能化等显著特点[1]。 新技术和新装备的出现大幅提高了目标的作战性能, 新环境和新干扰也使空战环境的变得更为复杂。 在这种情况下, 单枚导弹能够发挥的作用和实现的功能十分有限, 多导弹间的协同作战将变得越来越重要。
多弹协同是一个复杂的系统, 其中协同制导是协同攻击中的核心技术, 在协同作战中起关键作用[2]。 近年来, 国内外大量学者对协同制导开展了深入研究。 这些研究成果主要集中在多枚导弹攻击单个目标时, 将脱靶量、 攻击时间和攻击角度作为约束条件, 基于时空一致性原则来实现多导弹之间的协同[3]。 多弹对多目标的情况可以在多对一的基础上, 辅以航迹规划和任务分配实现。 郭正玉等[4-5]基于快速非奇异终端滑模理论设计了带有角度约束、 攻击大机动目标的三维空间多弹协同制导律, 但其未考虑俯仰平面和偏航平面之间的耦合, 且仿真时导弹速度恒定不变。 宋俊红等[6-9]将协同制导律的设计过程分成视线法向和视线方向两部分, 基于有限时间一致性理论和滑模控制理论设计了多弹协同制导律, 但公式复杂且需要的信息较多。 文献[10-12]基于领弹-从弹思路设计了多弹分布式协同制导控制方法, 但前提是假设导弹速度完全可控。 文献[13]提出了一种新型的基于领从式策略的三维时间协同制导律, 将对攻击时间的控制问题转化为从弹跟踪领弹的剩余弹目相对距离问题, 但假定导弹速度恒定, 攻击对象为静止目标。
目前, 研究较多的协同制导方法是以非奇异终端滑模理论为基础的有限时间收敛制导律, 其是从控制系统的稳定性出发推导出的非常复杂的控制律, 需要设计的参数较多, 不利于工程实现。 其次, 目前的研究大多在二维平面或者是认为俯仰平面和偏航平面没有耦合的伪三维空间, 在真三维空间的协同制导研究的不多, 且建立的模型过于理想, 或假设导弹速度完全可控, 或假设导弹速度为固定常值, 这对于使用固体火箭发动机的空空导弹来说都是不适用的。
针对上述问题, 本文提出了空空导弹弹道超实时仿真方法, 并设计了弹道成型角度约束制导律, 在六自由度环境中进行仿真分析, 验证了所提方法的有效性、 合理性和工程实用性。
1 弹道超实时仿真方法
超实时仿真是指系统仿真模型的时间过程快于实际系统的仿真研究, 运行一次仿真用时极少, 这一技术大多应用在航天器故障诊断、 预测控制、 辅助决策等领域[14]。 本文借鉴超实时仿真的思想, 通过建立导弹、 目标的简化运动模型, 利用最优制导律闭合制导回路, 构建系统的超实时仿真模型。 该模型能以导弹当前的攻击态势作为输入信息, 按一定的周期在较短时间内快速解算剩余的飞行弹道。 在导弹飞行过程中, 可以根据超实时仿真结果得到未来的弹道信息, 为在线预测、 评估导弹的制导控制效果提供了可能, 也为在线进行弹道规划、 参数优化和制导控制策略的及时调整奠定了基础。
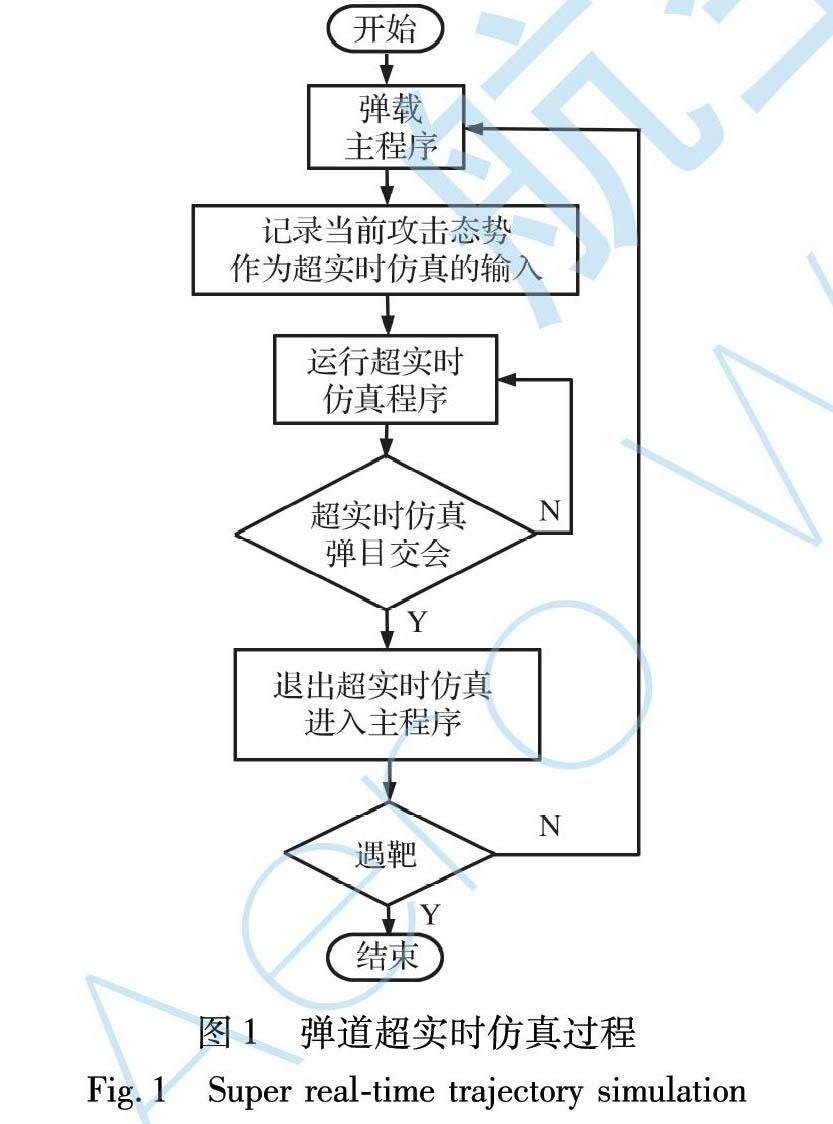
本文利用弹道超实时仿真方法, 快速、 超前预测弹道信息的特点, 准确估计每个导弹对应的剩余飞行时间, 综合所有导弹的超实时仿真结果, 在线调整每个导弹的控制过载, 形成闭环控制, 最终满足多弹攻击时间和攻击角度的双重约束。 弹道超实时仿真过程如图1所示。
从图1可知, 超实时仿真嵌套在正常彈道仿真程序之中, 相当于在正常弹道仿真程序中存在一个运行速度极快的数字仿真模型, 按照设定的周期循环调用超实时仿真模型。 超实时仿真可以在导弹飞行过程中根据当前的攻击态势快速进行弹道仿真, 从而在导弹未真正遇靶前, 提前得到飞行弹道未来的许多信息。
2 超实时仿真模型
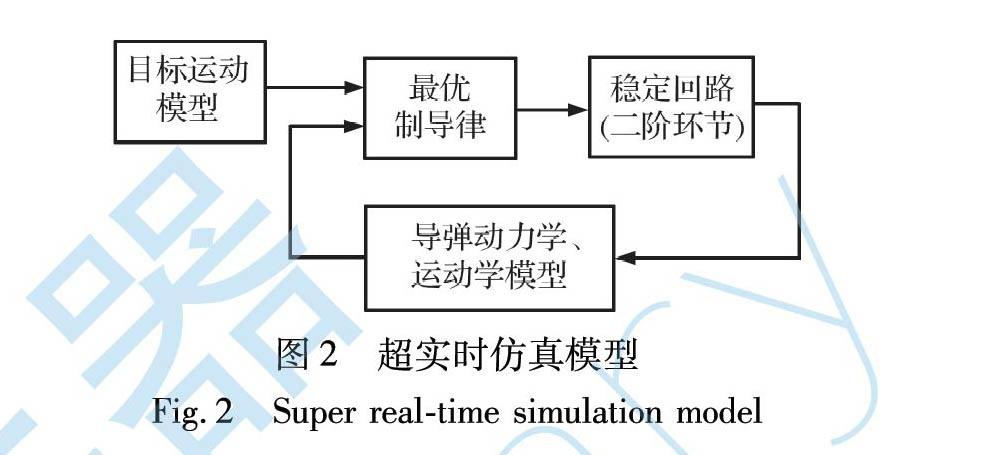
本文建立的超实时仿真模型框图如图2所示, 主要由目标运动模型、 导弹运动学/动力学模型、 最优制导律及稳定回路组成, 不考虑导引头和舵机等环节。
为了保证运算速度, 需对超实时仿真模型进行合理的简化。 为了保证后续进行弹道规划、 参数优化和制导控制策略调整的有效性, 超实时仿真模型的仿真结果与六自由度模型的仿真结果需要具有较高的拟真度, 在典型条件下本文建立的超实时仿真模型与六自由度模型的拟真度仍达到90%以上。
2.1 目标运动模型
假设目标在剩余飞行时间内以当前速度作匀速运动, 其运动模型为
vc=vc0(1)
rc=rc0+vc·h(2)
式中: vc, rc分别为目标的速度和位置矢量; vc0, rc0分别为目标在当前态势下的初始速度和位置矢量; h为积分步长。
2.2 导弹运动模型
在建立导弹运动学、 动力学模型时进行如下考虑:
(1) 导弹质量、 发动机推力根据飞行时间进行一维插值, 大气密度和音速根据导弹海拔高度计算。
(2) 导弹气动阻力系数中的零升阻力系数cx0和底阻系数cxd根据马赫数进行一维插值, 诱导阻力系数cxi与导弹攻角的平方成正比。
(3) 稳定回路简化为二阶环节, 表达式为
am=1T2s2+2·ξ·T·s+1·ac1(3)
式中: am为导弹横向加速度; ac1为弹体系加速度指令; T为导弹稳定回路时间常数; ξ为阻尼比。 阻尼比和时间常数分别是马赫数和动压的函数。
(4) 利用二阶微分方程求取导弹横向加速度的二阶导数a¨m, 表达式为
a¨m=(ac1-am-2·T·ξ·a·m)/T2(4)
導弹横向加速度由式(4)积分得到。
(5) 弹体系轴向加速度计算时, 考虑推力和速度坐标系中迎面阻力的作用, 表达式为
ax1=p/m+xv/cosαm(5)
式中: p为发动机推力; m为导弹质量; xv为迎面阻力所产生的纵向加速度分量(速度坐标系中), 根据阻力系数计算; αm为导弹攻角。
(6) 导弹速度矢量在惯性系的旋转角速度计算表达式为
ωv=vr×acv2 (6)
式中: vr, ac分别为导弹惯性系下的速度和加速度矢量; v为导弹速度模值。 通过惯性系到弹体系转换矩阵将旋转角速度转到弹体系:
ωv1=Cbi·ωv(7)
式中: Cbi为转换矩阵, 与导弹的姿态角有关。
(7) 导弹相对于弹体坐标轴y1/z1的旋转角速度表达式为
ωx1=(ωy1·cosγm-ωz1·sinγm)·tanm
ωy1=α·z+ωvy1-k3·(αzk-αz)
ωz1=α·y+ωvz1-k3·(αyk-αy) (8)
式中: αyk和αzk为运动学攻角; αy和αz为y和z通道攻角; α·y和α·z为y和z通道攻角导数; ωvy1和ωvz1为弹体系角速度矢量; k3为系数。 由导弹相对于弹体系的旋转角速度可以对导弹姿态进行更新。
(8) 将弹体系下导弹的加速度转换到惯性系, 即
ac=Cib·ac1 (9)
然后通过积分得到导弹在惯性系下的速度和位置:
vr=vr0+ac·h(10)
rr=rr0+vr·h(11)
(9) 弹目相对位置、 速度矢量关系:
ro=rc-rr(12)
vo=vc-vr(13)
2.3 最优制导律模型
以导弹所用控制能量最少和终端脱靶量最小为指标, 推导最优制导律的基本形式为[15]
ac=N·ro+vo·tgot2go+N2·at+K·g(14)
式中: N为导航比; tgo为剩余飞行时间; at为目标加速度估值矢量; K为重力加速度补偿系数; g为重力加速度矢量。
3 利用超实时仿真估计剩余飞行时间
在剩余飞行时间估算中, 国内外广泛使用当前的弹目相对距离除以弹目平均接近速度, 计算时假设目标在剩余飞行时间内作匀速运动, 导弹的平均速度一般通过估计的轴向加速度计算[16-18]。 导弹轴向加速度受发动机推力和气动阻力的影响, 鉴于导弹未来飞行轨迹的不可预知性, 导弹剩余飞行时间内的气动阻力不可能计算准确, 因此导弹的平均速度和剩余飞行时间的计算也不准确, 这会影响导弹对目标的精确打击能力。
弹道超实时仿真能够以当前的攻击态势为输入, 快速仿真导弹拦截目标的过程。 运行结束后便可得到导弹的飞行速度变化情况, 据此计算导弹的平均速度等相关信息, 从而可以对剩余飞行时间进行更加准确的计算。
剩余飞行时间超实时估计方法:
(1) 记录当前时刻及当前时刻导弹的姿态信息、 导弹和目标的位置、 速度信息, 作为超实时仿真模型的输入, 其中当前时刻用来插值计算发动机推力和导弹质量。
(2) 根据以上输入, 在设定的周期内运行弹道超实时仿真程序, 当运行至弹目交会时, 跳出并记录本次仿真的导弹速度、 飞行时间等信息。
(3) 由记录的超实时仿真结果计算导弹剩余飞行时间内的平均速度和弹目平均接近速度, 根据当前弹目距离可准确估算剩余飞行时间。
4 多弹协同制导律设计
多弹协同制导律的设计需要考虑更多的约束, 包括攻击时间、 编队队形、 末端攻击角度等。
4.1 多弹协同制导模型
导弹与目标的相对运动学方程可以表示为
r·i=Vtcosθt-Vmicosθmi
λ·i=Vtsinθt-Vmisinθmiri
γ·mi=amiVmi
γ·t=atVt (15)
式中: θm=γm-λ; θt=γt-λ。
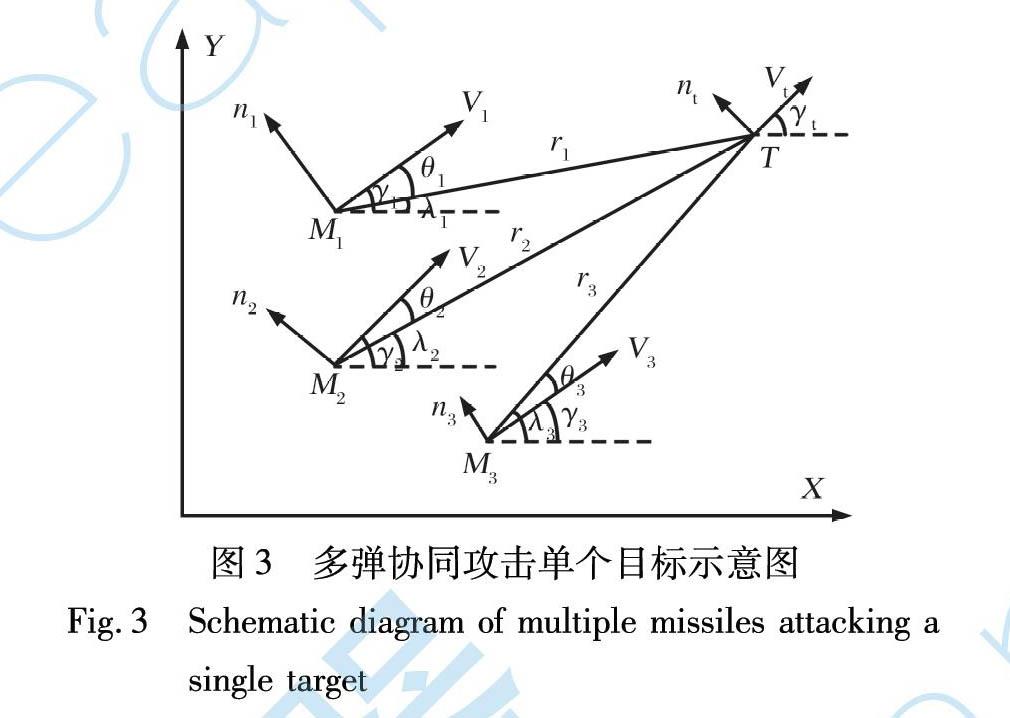
图3给出了多枚导弹打击单个目标的示意图。 图中ri为第i枚导弹的弹目距离; Vi为第i枚导弹的速度; ai为第i枚导弹的法向加速度; γi为第i枚导弹的航向角; λi为第i枚导弹的视线角; θi为第i枚导弹的前置角。
4.2 带攻击时间约束的协同制导律设计
目前, 在多弹协同制导律设计时, 一般都假设导弹速度可控或恒定, 这不符合实际情况。 由于沿弹轴方向的加速度不可控, 所以导弹的控制过载只能施加在弹体系的y1, z1两个方向。 为了保证多弹攻击时间基本一致, 本文利用弹道超实时仿真方法估计每枚导弹的剩余飞行时间, 控制剩余飞行时间小的导弹在水平面内做机动, 以增大飞行路程, 达到和其他导弹同时遇靶的目的。
考慮到建模误差及飞行过程中的各种干扰, 很难找到水平面控制过载与剩余飞行时间误差之间明显的对应关系, 本文利用弹道超实时仿真用时少的优势, 快速预测施加的水平面控制过载达到的效果, 根据剩余飞行时间误差的大小, 在线实时调整水平面的控制过载, 达到时间协同的控制目的。
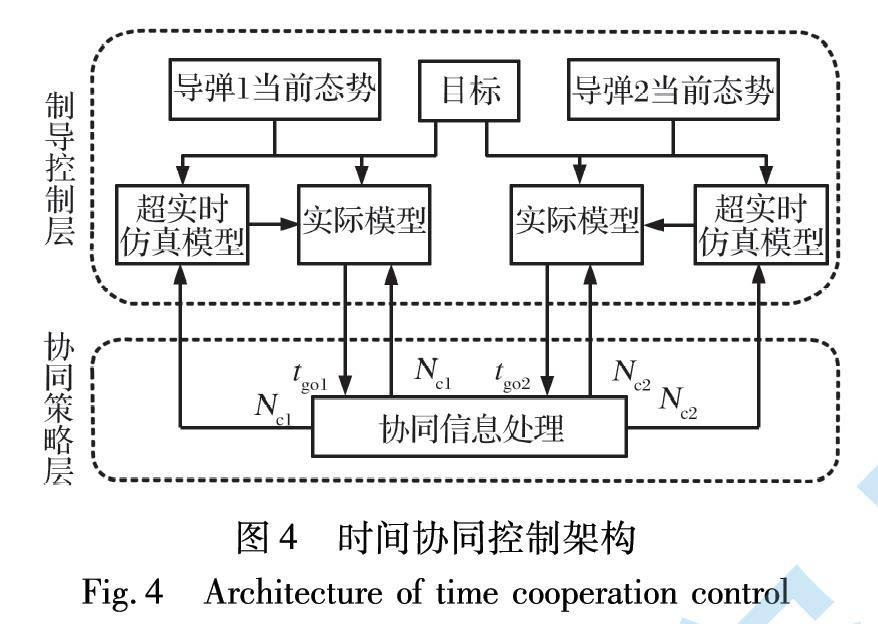
以2枚导弹为例, 图4给出了采用双层架构的协同信息交互方式及时间协同控制的基本架构。 协同策略层综合超实时仿真预测的弹道信息和导弹的剩余飞行时间信息, 生成协同控制指令反馈给制导控制层, 导弹依据反馈的信息进行制导控制飞行。
可见, 水平面的机动是以协调变量剩余飞行时间保持一致进行的闭环控制, 通过改变水平面控制过载的大小来实现, 不干涉铅锤面控制过载的正常计算。
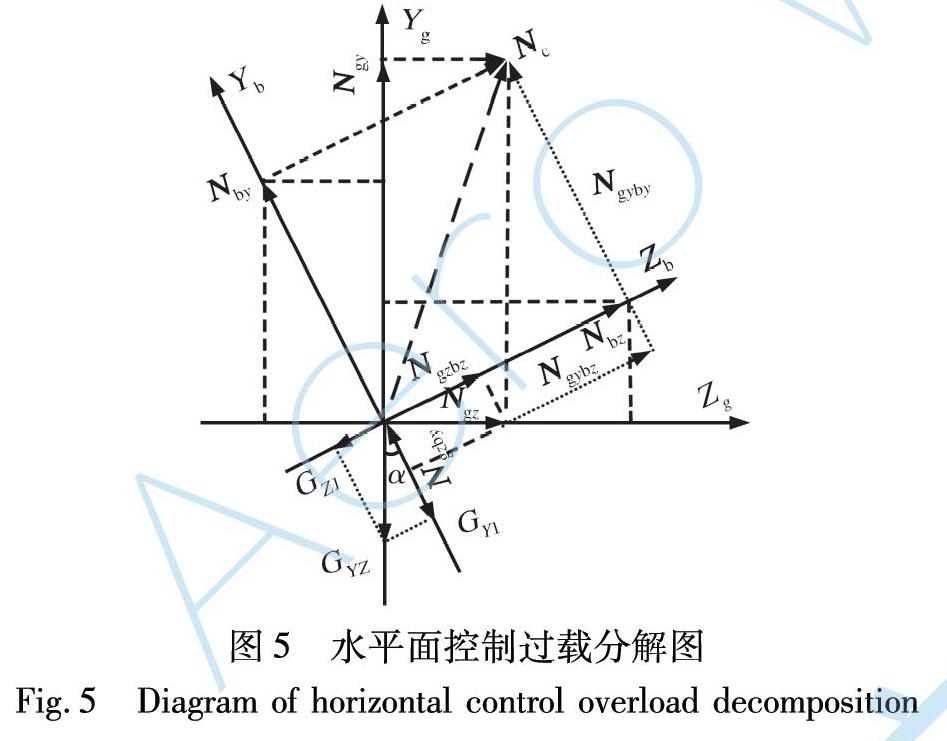
如图5所示, 惯性系控制过载矢量Nc按照式(14)进行计算, 其在水平面和铅垂面的分量分别为Ngz, Ngy, 在弹体系的分量分别为Nbz, Nby。 控制开始时水平面附加的控制过载为Nzf, 控制剩余飞行时间小的导弹在水平面内进行机动, 该控制过载与多枚导弹之间的剩余飞行时间的差值有关。 过载向量Ngz, Ngy和Nzf在弹体系的分量分别为Ngzby, Ngzby, Ngyby, Ngybz, Nzfby, Nzfbz。 从而可以得到弹体系的控制过载为
Nby=Kz·Ngzby+Ngyby+Nzfby
Nbz=Kz·Ngzbz+Ngybz+Nzfbz(16)
式中: Kz为不大于1的修正系数。
4.3 带攻击角度约束的协同制导律设计
多导弹攻击单一目标时, 对每枚导弹的攻击角度进行约束可以达到避免多弹碰撞、 提高杀伤效果的目的。 本文的攻击角度约束指的是弹目视线矢量与目标速度矢量之间的夹角在遇靶时满足设计要求, 这样还能保证较小的脱靶量。 下面基于弹道成型制导理论设计具有攻击角度约束的制导算法。
弹道成型制导律的简化形式为[15]
Nc=6r+4r·tgo+2r·(tf)tgot2go+nt(17)
式中: r为相对位置; r·为相对速度; tf为终端遇靶时刻; tgo为剩余飞行时间; nt为目标机动过载。
经过数学运算, 式(17)可变换为
Nc=4Vcλ·+2Vc(λ-λf)tgo+nt(18)
式中: λ·=r+r·tgoVct2go为视线转动角速度; Vc为弹目接近速度; λf为设定的终端视线角。 弹道超实时仿真可以提前预测出该角度的大小, 基于此设计终端的攻击角度约束。
需要说明的是, 以上带攻击时间和攻击角度约束的制导律都是基于导弹完整的六自由度模型, 在三维空间设计的, 导弹的控制过载在惯性系计算, 转到弹体系进行实现。
5 仿真验证
为验证本文提出的多弹协同制导律的有效性, 设计仿真条件进行数字仿真。 仿真场景: 3枚导弹挂装在2架载机上, 从不同的时刻发射后协同攻击1个目标。
5.1 仿真条件设计
数字仿真条件: 2架载机的横向间距为4 km, 高差为1 km, 导弹均为迎头发射, 其中1号和3号导弹挂装在同一架载机上, 1号导弹发射时弹目距离为70 km。 3枚导弹的发射时刻和遇靶时刻的攻击角度约束详见表1。
5.2 仿真结果与分析
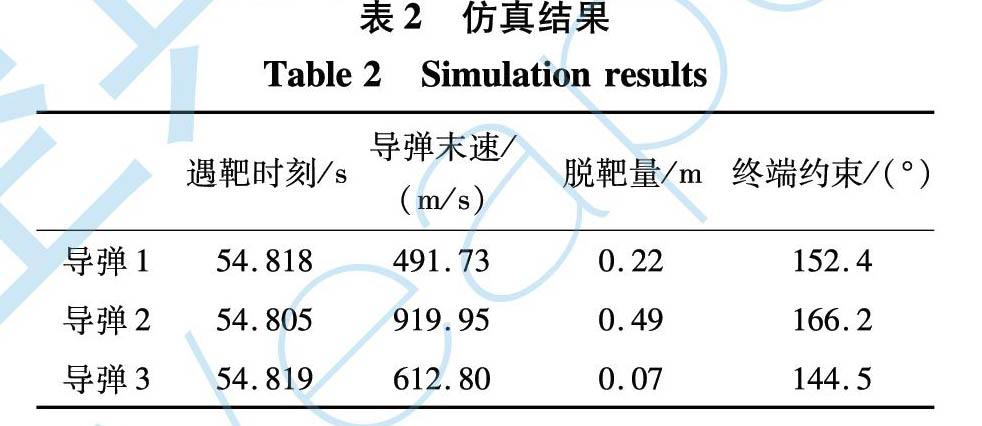
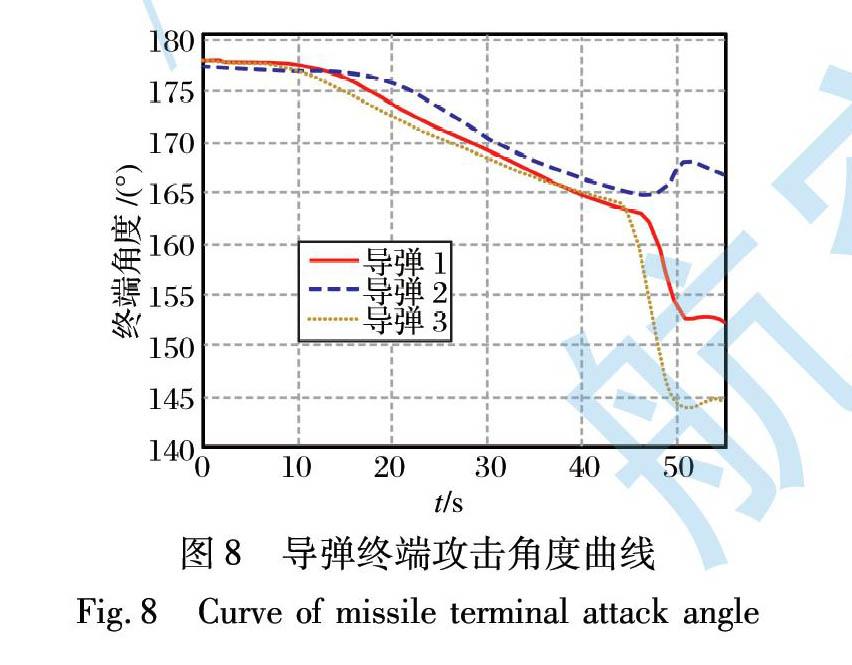
在六自由度仿真环境下进行弹道仿真, 仿真得到的结果统计如表2所示, 从表中可知, 3枚导弹基本按照设计的约束在同一时刻遇靶, 验证了具有攻击时间和攻击角度约束的协同制导律的有效性, 同时给出了以1号导弹发射时刻为零点的相关变量变化曲线。
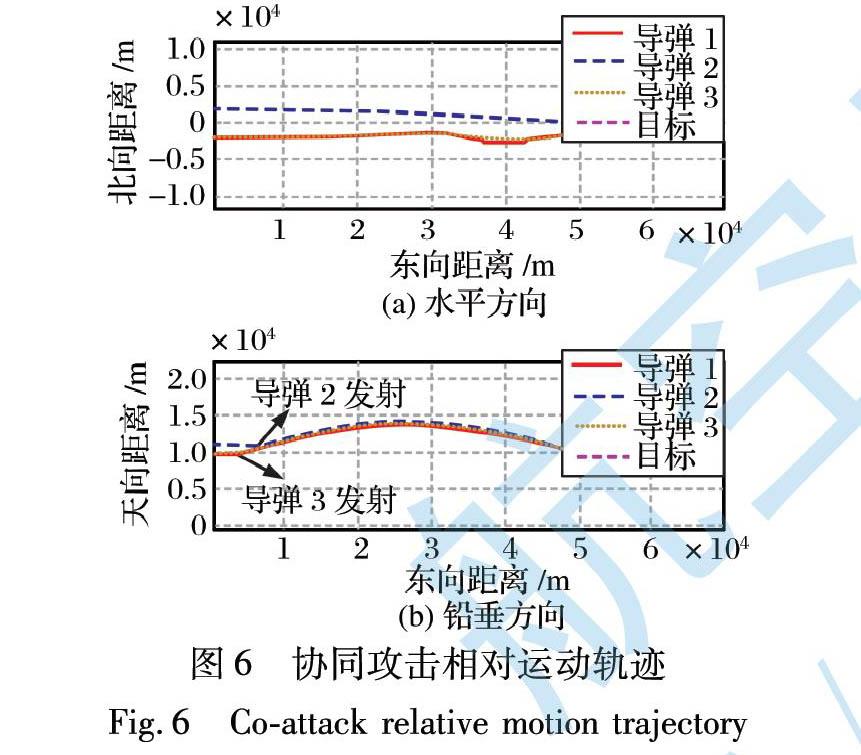
图6所示为3枚导弹协同攻击单个目标的相对运动轨迹, 可以明显看出, 为了达到同时遇靶的设计目标, 1号和3号导弹在东向飞行约31 km后开始在水平面机动, 弹道发生弯曲, 而2号导弹的弹道较为平直。
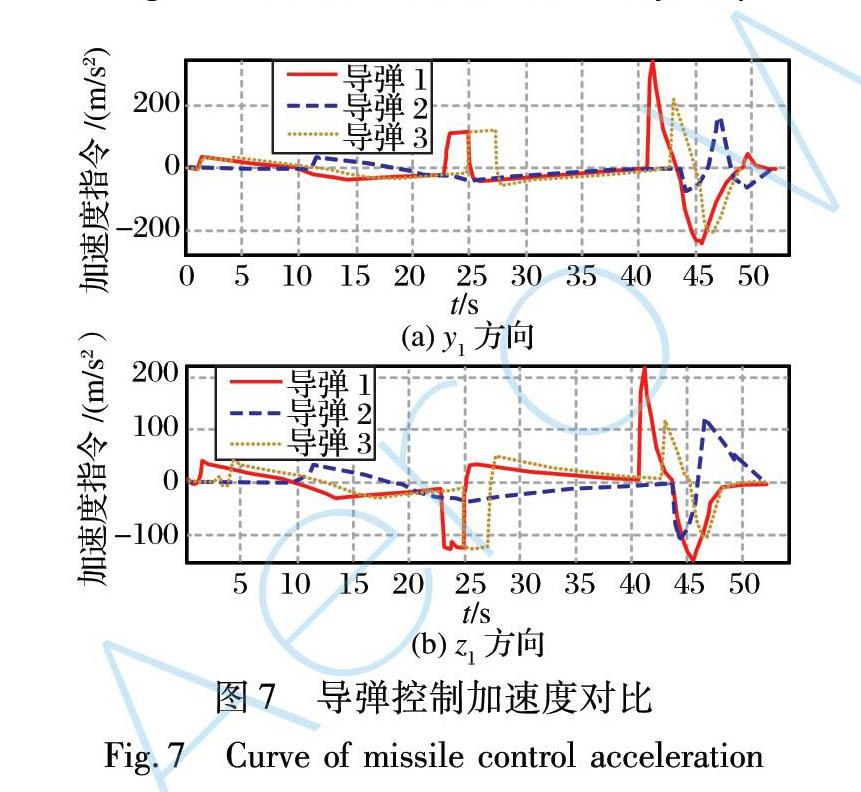
图7为3枚导弹弹体系y1, z1方向的控制过载变化曲线对比, 从过载变化情况看出, 先发射的1号和3号导弹在发射后22.5 s和25 s开始在水平面机动, 以增大飞行路程和飞行时间, 等待与后发射的2号导弹同时遇靶, 付出的代价是1号和3号导弹的末速较低, 当然这也与发射时弹目距离远有关系。 最后发射的2号导弹在水平面内没有额外机动, 直接对目标发起攻击。 从曲线中也可以看出, 3枚导弹分别在41.5 s, 42.5 s, 43 s开始进行末端攻击角度约束的调整控制。
图8为3枚导弹弹目视线与目标速度矢量夹角的变化曲线, 可以看出, 在弹道末端基本实现了设定的角度约束要求。
6 结 论
本文通过建立弹道超实时仿真模型, 探讨了一种在导弹速度不可控的条件下, 适用于工程应用的、 多枚导弹同时满足攻击时间和末端攻击角度约束的协同制导方法, 并在六自由度仿真环境中, 通过数字仿真对所提出的制导方法的有效性进行了验证。
该方法利用超实时仿真对弹道未来信息进行预测, 建立了多弹飞行时间误差与水平面控制过载之间的闭环调节方式, 但时间协同约束对多枚导弹的发射条件具有一定的局限性。 比如, 如果发射时刻间隔太长或发射条件差异太大, 就难以实现多弹攻击时间上的协同, 且对导弹的末速有较大影响, 反而会降低对目标的毁伤效果。
接下来会进一步研究该方法的适用范围, 同时将该方法推广至攻击机动目标的协同制导研究中。
参考文献:
[1] 樊会涛, 张蓬蓬. 空空导弹面临的挑战[J]. 航空兵器, 2017(2): 3-7.
Fan Huitao, Zhang Pengpeng. The Challenges for Air-to-Air Missile[J]. Aero Weaponry, 2017(2): 3-7.(in Chinese)
[2] 槐澤鹏, 梁雪超, 王洪波, 等. 多弹协同及其智能化发展研究[J]. 战术导弹技术, 2019(5): 77-85.
Huai Zepeng, Liang Xuechao, Wang Hongbo, et al. Research on Multi-Missile Collaborative and Its Intelligence Development[J]. Tactical Missile Technology, 2019(5): 77-85.(in Chinese)
[3] 杨剑影, 周佳玲, 魏小倩. 多导弹攻击高机动目标的分布式协同制导关键技术[J]. 航空兵器, 2017(3): 3-12.
Yang Jianying, Zhou Jialing, Wei Xiaoqian. Key Technologies of Distributed Cooperative Guidance and Control Method for Multiple Missiles Attacking the Maneuvering Target[J]. Aero Weaponry, 2017(3): 3-12.(in Chinese)
[4] 郭正玉, 韩治国. 基于快速非奇异终端滑模的多弹协同制导律设计[J]. 航空兵器, 2020, 27(3): 62-66.
Guo Zhengyu, Han Zhiguo. Multi-Missile Cooperative Guidance Law Design Based on Fast Non-Singular Terminal Sliding Mode[J]. Aero Weaponry, 2020, 27(3): 62-66.(in Chinese)
[5] 郭正玉, 王超磊, 钱航, 等. 带有攻击角约束的大机动目标协同攻击制导律[J]. 西北工业大学学报, 2020, 38(6): 1257-1265.
Guo Zhengyu, Wang Chaolei, Qian Hang, et al. Cooperative Intercepting Guidance Law for Large Maneuvering Target with Impact Angle Constraint[J]. Journal of Northwestern Polytechnical University, 2020, 38(6): 1257-1265.(in Chinese)
[6] 宋俊红, 宋申民, 徐胜利. 带有攻击角约束的多导弹协同制导律[J]. 中国惯性技术学报, 2016, 24(4): 554-560.
Song Junhong, Song Shenmin, Xu Shengli. Cooperative Guidance Law for Multiple Missiles with Impact Angle Constraints[J]. Journal of Chinese Inertial Technology, 2016, 24(4): 554-560.(in Chinese)
[7] Wu P, Yang M. Integrated Guidance and Control Design for Missile with Terminal Impact Angle Constraint Based on Sliding Mode Control[J]. Journal of Systems Engineering and Electronics, 2010, 21(4): 623-628.
[8] Saleem A, Ratnoo A. Lyapunov-Based Guidance Law for Impact Time Control and Simultaneous Arrival[J]. Journal of Guidance, Control, and Dynamics, 2015, 39(1): 164-173.
[9] Chen X T, Wang J Z. Nonsingular Sliding-Mode Control for Field-of-View Constrained Impact Time Guidance[J]. Journal of Gui-dance, Control, and Dynamics, 2018, 41(5): 1214-1222.
[10] 孙雪娇, 周锐, 吴江, 等. 多导弹分布式协同制导与控制方法[J]. 北京航空航天大学学报, 2014, 40(1): 120-124.
Sun Xuejiao, Zhou Rui, Wu Jiang, et al. Distributed Cooperative Guidance and Control for Multiple Missiles[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(1): 120-124.(in Chinese)
[11] 邹丽, 孔繁峨, 周锐, 等. 多导弹分布式自适应协同制导方法[J]. 北京航空航天大学学报, 2012, 38(1): 128-132.
Zou Li, Kong Fan’e, Zhou Rui, et al. Distributed Adaptive Cooperative Guidance for Multi-Missile Salvo Attack[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(1): 128-132.(in Chinese)
[12] 劉翔, 梁晓庚. 攻击角约束多拦截弹协同制导控制一体化研究[J]. 西北工业大学学报, 2019, 37(2): 273-282.
Liu Xiang, Liang Xiaogeng. Integrated Guidance and Control of Multiple Interceptors with Impact Angle Constraints Considered[J]. Journal of Northwestern Polytechnical University, 2019, 37(2): 273-282.(in Chinese)
[13] 张振林, 张科, 郭正玉, 等. 一种新型领从式多弹协同制导律设计[J]. 航空兵器, 2020, 27(5): 33-38.
Zhang Zhenlin, Zhang Ke, Guo Zhengyu, et al. Design of a New Guidance Law for Guided Multiple Missiles[J]. Aero Weaponry, 2020, 27(5): 33-38.(in Chinese)
[14] 高薇, 张强, 孙军. 通过超实时仿真验证轨控策略方法研究[J]. 航天控制, 2008, 26(2): 71-73.
Gao Wei, Zhang Qiang, Sun Jun. Method of Validating Orbit Control Strategy by Super Real-Time Simulation[J]. Aerospace Control, 2008, 26(2): 71-73.(in Chinese)
[15] Zarchan P.Tactical and Strategic Missile Guidance[M]. Washington: American Institute of Aeronautics and Astronautics, Inc, 1997.
[16] Tahk M J, Ryoo C K, Cho H. Recursive Time-to-Go Estimation for Homing Guidance Missiles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 13-24.
[17] Lee G K F. Estimation of the Time-to-Go Parameter for Air-to-Air Missiles[J]. Journal of Guidance, Control, and Dynamics, 1985, 8(2): 262-266.
[18] Ryoo C K, Tahk M J, Cho H. Practical Time-to-Go Estimation Methods for Optimal Guidance[C]∥Guidance, Navigation, and Control Conference and Exhibit, 1999.
Research on Cooperative Guidance Law of Multi-Missile
Based on Trajectory Super-Real Time Simulation
Zhang Peng1*, Lu Hao1, Shen Xin2
(1.China Airborne Missile Academy, Luoyang 471009, China;
2.The First Military Representative Office of Air Force Equipment Department in Luoyang, Luoyang 471009, China)
Abstract: It is very difficult to conduct time cooperation guidance of multi-missile when the velocity of missile is uncontrollable. Based on the trajectory super real-time simulation method, which can gives out time-to-go exactly as well as future trajectory information, a closed-loop control system between the horizontal control overload and the flight time error of missiles is built. So that the flight time tends to be consistent and the cooperative impact time is realized. In addition, a trajectory shaping guidance law with impact angle constraints is designed. The designed guidance law is verified by 6-DOF simulation, and the results show that the multi-missile cooperative guidance law based on the super real-time trajectory simulation can guarantee that multi-missile hit the target with the desired impact angle simutaneously.
Key words: cooperative guidance law; impact time constraint; impact angle constraint; super real-time simulation; time-to-go; multi-missile coordination
