拦截机动目标的多导弹协同制导律

马萌晨 宋申民

摘 要：面向多导弹协同拦截机动目标的问题， 基于剩余飞行时间控制， 设计了两种不同的协同制导律。 针对多导弹分布式通信的场景， 基于偏置比例导引的思想设计了具有时变导航系数的分布式协同比例制导律; 针对指定攻击时间的场景， 基于常值前置角下的剩余飞行时间形式， 利用滑模控制和非线性扰动观测器设计了具有指定攻击时间的滑模制导律。 仿真结果表明， 所设计的两种制导律可以有效针对机动目标实施协同攻击或依次攻击。

关键词：     机动目标; 剩余飞行时间; 偏置比例导引; 非线性扰动观测器; 滑模控制; 多导弹协同; 制导律

中图分类号：     TJ765.3; V448  文献标识码：    A  文章编号：     1673-5048（2021）06-0019-09

0 引  言

现代战争是体系与体系之间的对抗， 随着通信组网技术的发展， 多导弹协同作战正逐步成为现代战场中的重要作战模式之一。 多导弹之间通过通信实现对目标的协同感知、 协同探测与协同攻击， 可以最大限度地利用和协调导弹系统资源， 提高导弹的整体作战效能。

在多导弹协同制导律设计方面， 国内外相关学者进行了大量的研究。 文献[1]较早开展了攻击时间控制的研究， 针对反舰导弹， 基于最优控制理论， 通过在传统比例制导律的基础上增加攻击时间误差反馈项， 设计了多导弹攻击时间协同制导律， 并给出导弹剩余飞行时间的近似求法。 在此基础上， 文献[2]增加了具有终端攻擊角约束的附加项， 实现了同时具有攻击角度和攻击时间控制的协同制导律。 文献[3]通过引入剩余飞行时间方差的概念， 设计了分布式时间协同制导律， 并给出一种剩余飞行时间形式的理论推导。 文献[4]通过设计含有攻击时间误差和导弹前置角的新型滑模面， 设计了攻击时间可控的滑模制导律， 但该制导律存在不连续的问题。 文献[5]直接将攻击时间误差设计为滑模面， 并通过引入一个连续的非线性函数， 设计了攻击时间可控的非奇异滑模制导律。 文献[6]针对导弹在三维空间攻击固定目标场景， 考虑导弹飞行过程中的视场角约束， 基于一致性算法设计了带有视场角约束的三维时间协同制导律。 文献[7]为减少由于剩余飞行时间估计不准产生的误差， 基于领从式制导架构， 将制导律的攻击时间控制问题转换为从弹跟踪领弹的剩余弹目相对距离问题， 并通过解耦得到俯仰和偏航通道的控制量。 文献[8]基于领从架构， 采用超螺旋控制方法设计了攻击时间控制制导律， 提高了所设计制导律的鲁棒性与平稳性。 文献[9]在具有角度约束的最优制导律基础上， 引入攻击时间控制修正量， 通过在线的调整领弹和从弹， 设计了具有攻击时间和角度约束的协同制导策略。 文献[10]针对高超声速飞行器， 在滑翔段通过设计两阶段的协同航迹规划， 实现了攻击时间和攻击角度的约束， 该方法为调整导弹的攻击时间和攻击角度提供了新的思路。 但上述方法大多是针对舰船等静止或低速移动目标所设计， 对于运动及机动目标缺乏严谨有效的理论分析。

在针对运动目标的协同制导律设计方面， 文献[11]针对低速运动目标， 通过将目标运动引起的剩余飞行时间变化视为扰动， 利用线性扩张状态观测器对其估计并进行补偿， 基于固定时间收敛控制理论， 设计了攻击时间控制协同制导律。 文献[12]基于滑模控制， 设计了一种可指定攻击时间的非奇异滑模制导律， 并在此基础上， 采用虚拟目标的设计思路， 将制导律扩展到机动目标的应用场景中。  文献[13]针对静止和机动目标，  分别设计了分布式和集中式的协同制导律， 但缺乏严谨的理论分析和证明。 文献[14]基于导弹和运动目标的相对运动学模型， 推导了一种新型的剩余飞行时间形式， 并设计了针对运动目标和机动目标的攻击时间控制制导律。 文献[15-16]基于一致性理论， 利用滑模控制方法针对机动目标分别从视线和视线法向方向设计制导律来控制导弹的攻击时间和攻击角度， 但该方法要求导弹轴向推力可控， 条件太过苛刻。 文献[17]研究了切换通信拓扑条件下， 多枚导弹采用领从制导体制协同拦截机动目标的时变编队制导问题， 通过控制从弹跟踪期望的时变编队， 实现了多导弹对机动目标的协同拦截。 文献[18]针对三维场景下， 多枚弱机动导弹协同拦截强机动目标的问题， 通过将导弹的可达区域在二维空间下表示， 提出一种基于协同覆盖策略的协同制导律， 实现了多枚弱机动导弹在加速度受限情况下， 对强机动目标的协同拦截， 该方法具有较强的工程实用性。

基于上述讨论， 为了处理导弹轴向不可控情况下， 多导弹协同拦截机动目标的协同制导问题， 分别采用在线和离线设计剩余飞行时间的思想， 设计了分布式时间协同制导律和指定攻击时间制导律， 从而实现了对机动目标的同时或依次攻击。

1 制导模型及剩余飞行时间计算

首先给出导弹和目标在二维平面内的制导模型示意图， 如图1所示。

图中， M和T分别表示导弹和目标; R表示导弹和目标之间的相对距离; Vm和Vt分别为导弹和目标的速度; θm和θt为导弹和目标的前置角; θL表示视线角。 则制导模型的动力学方程可以表述为

R·=Vtcosθt-Vmcosθm=Vr（1）

Rθ·L=Vtsinθt-Vmsinθm=Vθ（2）

θ·m=amVm-θ·L（3）

θ·t=atVt-θ·L（4）

对导弹剩余飞行时间（time-to-go，  tgo）的估算是针对机动目标实现协同攻击的前提， 对剩余飞行时间的研究不仅需要研究如何更准确地估算出导弹的攻击时间， 还要兼顾考虑其动力学模型是否可控。 现阶段， 针对打击机动目标的剩余飞行时间， 由于目标机动的未知性， 尚无有效精确的数学解析式， 大多采用通过一些假设来求得近似的剩余飞行时间。 因此， 给出以下三种常用的剩余飞行时间的表达式， 并对其特性进行分析。

（1）基于比例导引的剩余飞行时间tgo1

若导弹M采用比例制导律， 则根据文献[3]， 可较精确地估计得到导弹M的tgo1为

tgo1=RVm1+θ2m2（2N-1）（5）

式中： N为导航系数， 满足2<N<6。

tgo1在推导过程中用到了目标静止和前置角为小量的假设条件， 实质上是导弹航向误差的函数。 通常认为该形式的剩余飞行时间针对静止目标有效; 而针对机动目标， 该形式的剩余飞行时间则会因目标运动存在一定的估计误差。 因此， 针对机动目标， tgo1通常不能用来直接控制具体的剩余飞行时间。

（2） 瞬時剩余飞行时间tgo2

瞬时剩余飞行时间的定义为

tgo2=RVc（6）

式中： Vc为导弹和目标在视线方向上的接近速度。

tgo2定义为当前时刻导弹距目标的距离除以当前时刻导弹和目标的接近速度。 其物理定义简单， 被广泛应用于对导弹的剩余飞行时间的计算中。 然而该形式的剩余飞行时间未考虑导弹和目标的机动带来的影响， 只能表征当前时刻下导弹和目标的瞬时剩余飞行时间。 在使用tgo2来调节导弹的飞行时间时， 由于其表达式分母为导弹和目标的接近速度， 对于具有较大初始误差的情形， 导弹需要进行较大的机动来调整飞行轨迹， 进而消除飞行时间误差， 这可能会引起导弹和目标接近速度符号的改变， 进而造成奇异问题。 因此， 对于多导弹协同制导而言， 该形式的剩余飞行时间通常适用于弹群初始tgo2相差不大的情形。

（3） 基于常值前置角的剩余飞行时间tgo3

文献[14]从导弹和目标的相对运动学方程出发， 推导了在目标机动为0、 导弹前置角为常值下的剩余飞行时间的形式：

tgo3=R[Vr+2Vmcosθm-Vθtanθm]V2m-V2t（7）

在tgo3推导过程中， 要求运动目标的机动加速度为0且导弹前置角为常值， 其更像是针对运动目标拦截的一个特殊场景。 相比于tgo1， tgo3在推导过程中是直接基于导弹和运动目标的相对运动学方程， 没有运用任何假设和近似条件; 相比于tgo2， tgo3不会发生奇异问题。 在针对机动目标的tgo估计中， 受目标机动影响， 虽然仍有一定的估计误差， 但相比于tgo1和tgo2， 其估计精度更高且应用场景更广。 因此， tgo3可以直接用来对导弹的剩余飞行时间进行设计。 这将在下一节协同制导律的设计中体现。

2 时间协同制导律设计

2.1 代数图论

在多导弹协同制导的过程中， 导弹通过通信与相邻的导弹交换状态信息， 这种通信拓扑关系可以由图论来表示。 在本文中， 多导弹之间的通信网络由无向图G=（v， ζ， C）来描述，  v表示图G中所有节点组成的集合; ζ代表图G中节点之间的连线; 矩阵C=[cij]∈Rn×n代表权系数矩阵， 若导弹i和导弹j之间能够信息交换， 则有cij=1， 否则cij=0， 特别的cii=0， i∈{1， 2， …， n}。 若G是无向图， 即若第i个导弹可以从第j个导弹获得信息， 则第j个导弹也可以从第i个导弹获得信息， 则有cij=cji。 如果无向图中任意两个节点都可以通过连线找到一条线路连接， 则称无向图为连通的。 定义图G（C）对应的拉普拉斯矩阵为L=[lij]∈Rn×n， 其中矩阵元素为

lij=∑nm=1， m≠icim，  j=i-cij，  j≠i （8）

当多导弹之间的通信拓扑是无向且连通时， 则有下述假设和引理成立。

引理1[19]： 对于拉普拉斯矩阵L， 0是一个特征值， 并且满足所有非零特征值都是正数， 所有项为1的列向量为其一个特征向量。

引理2[20]： 对任意的x∈Rn， 如果满足1Tx=0， 则有xTLx≥λ2（L）xTx成立， 其中， λ2（L）表示矩阵L的最小非零特征值。

引理3[21]： 考虑非线性系统x·=f（x， t）， x∈Rn， 假设存在一个连续正定、 径向无界的函数V（x）， 并且满足

V·（x）≤-μV（x）-λVα（x）（9）

式中： μ， λ>0以及0<α<1是常数， 则原点是该非线性系统全局有限时间稳定的平衡点。 x（t0）=x0， t0是初始时间， 那么系统状态到达平衡点的时间T满足

T≤1μ（1-α）lnμV1-α（x0）+λλ（10）

引理4[22]： 考虑非线性系统x·=f（x， t）， x∈Rn， 假设存在一个连续正定、 径向无界的函数V（x）， ε∈（0， 1）， c>0， 0<δ<∞， 使得

V·≤-cVε+δ（11）

则系统是实际有限时间收敛的。

2.2 基于比例加时间偏置项的分布式协同制导律

比例导引形式简单， 在工程中应用广泛。 在对比例导引的分析中发现， 比例导引的导航系数直接影响着导弹的飞行弹道。 因此， 可以通过改变比例导引的导航系数来改变导弹的攻击轨迹， 进而改变导弹的攻击时间。 文献[3]中针对静止目标， 设计了具有时变导航比的协同比例导引， 通过改变导航比来实现攻击时间的协同， 但该方法不能保证tgo的收敛时间。 文献[13]针对静止和机动目标， 通过在线改变导航系数， 分别设计了集中式和分布式的偏置比例导引， 但缺乏严谨的理论证明。 受文献[23]的启发， 针对tgo1的表达形式， 基于有限时间引理， 设计协同比例制导律如下：

ami=N-iVmiθ·LiN-i=Ni{1-k1isgn（ξi）-k2iξi}ξi=∑nj=1cij（tgoj-tgoi）（12）

证明： 首先将式（12）重新整理为

ami=N-i[1-k1isgn（ξi）-k2iξi]Vmiθ·Li（13）

对tgo1进行求导， 将式（13）代入， 并利用小角度假设化简， 即sinθm=θm， cosθm=1-12θ2m， θ4m≈0， 可得

t·goi=-1+θ2miN2N-1-θmiRi（2N-1）V2miN[1-

k1isgn（ξi）-k2iξi]Vmiθ·Li=-1+

Nθ2mi2N-1[k1isgn（ξi）+k2iξi]（14）

构造如下形式的李雅普诺夫函数：

V1=12∑nj=1cij（tgoj-tgoi）2=12tTgoLtgo（15）

式中： tgo=[tgo1， tgo2， …， tgon]T; L=[lij]∈Rn×n為图G（C）对应的拉普拉斯矩阵。

则一致性误差ξi可重写为

ξ=-Ltgo（16）

式中： ξ=[ξ1， ξ2， …， ξn]T。

由于导弹之间的通信拓扑图是无向且连通的， 因而cij=cji， 可得

∑ni=1ξi=∑ni=1∑nj=1cij（tgoj-tgoi）=0（17）

对V1求导， 并将上式带入可得

V·1=tTgoLt·go=-ξTt·go=

-∑ni=1ξi-1+Nθ2mi2N-1[k1isgn（ξi）+k2iξi]= ∑ni=1ξi-Nθ2miξi2N-1[k1isgn（ξi）+k2iξi]=

-N2N-1∑ni=1[θ2mi（k1iξi+k2iξ2i）]（18）

由于θmi>0， 假设在tgoi收敛之前θmi≠0， 则存在常数ε0>0， 使得θmi>ε0。 令k1=min{k11， k12， …， k1n}， k2=min{k21， k22， …， k2n}， 则上式可重写为

V·1=-N2N-1∑ni=1[θ2mi（k1iξi+k2iξ2i）]≤

-Nε202N-1k1∑ni=1ξi+k2∑ni=1ξ2i（19）

由引理1中拉普拉斯矩阵的性质可知L1=0， 因而有1TL1=（L121）T（L121）=0， 故L121=0。 进而有1TL12=0T， 故1TL12tgo=0。 由引理2和式（16）可知：

ξTξ=tTgoLLtgo=tTgoL12LL12tgo=

（L12tgo）TLL12tgo≥

[λ2（L）]（L12tgo）TL12tgo≥[λ2（L）]tTgoLtgo≥2[λ2（L）]V1（20）

将式（20）代入式（19）中可得

V·1=-Nε202N-1[k1（ξTξ）12+k2ξTξ]≤

-[2λ2（L）]12k1Nε202N-1V121-2k2[λ2（L）]Nε202N-1V1（21）

由引理3可知， 各导弹的剩余飞行时间tgoi可以在有限时间内收敛到一致。 至此， 证明完成。

注1： 所设计的协同比例制导律实质是在传统的比例制导律基础上加上时间误差偏置项组成， 其中ξi被称为导弹剩余飞行时间的一致性误差。 当ξi>0时， 表示第i枚导弹的剩余飞行时间小于与其具有通信交流的其他导弹的平均剩余飞行时间， 即表明该枚导弹剩余飞行时间较小， 需要增大其剩余飞行时间， 此时N-i会减小， 这表示导弹的飞行轨迹将更弯曲。 同样地， 当ξi<0时， 表示第i枚导弹的剩余飞行时间较大， 需要减小其剩余飞行时间， 此时N-i会增大， 这表示导弹的飞行轨迹将更平直。 当ξi≈0时， 此时制导律变为传统的比例导引， 从而保证对目标的有效打击。 实际上， 在式（12）的制导律形式中， 并不需要导弹非常精确的剩余飞行时间， 因为并没有通过tgo1去设计具体的攻击时间， 而是将其作为协调变量， 通过协调变量的变化在线调整制导律参数， 实现协同攻击。

注2： 上述制导律的推导是建立在导弹通信拓扑为无向且连通的情况下， 然而实际上， 对于有向图的情形， 当弹群中的导弹仅能与相邻的导弹进行单向通信时， 仍然满足式（17）的条件， 即制导律仍然成立， 这点将在仿真中予以验证。

2.3 基于非线性干扰观测器的指定攻击时间制导律

在针对诸如战机等机动目标的协同拦截时， 目标可能会在导弹来袭前某段时刻进行机动来躲避攻击， 若导弹总的末制导攻击时间可以提前指定， 则更有利于针对该类机动目标的协同拦截。

若要对导弹的攻击时间进行设计， 则需要用到导弹tgo的动力学模型。

基于tgo3进行制导律设计。 首先对tgo3进行求导并整理可得

t·go3=-1+V2θsec2θmV2m-V2t-RVθsec2θmVm（V2m-V2t）am-

Rsin（θm+θt）cosθm（V2m-V2t）at=F+Bam+D（22）

式中： F=-1+V2θsec2θmV2m-V2t; B=-RVθsec2θmVm（V2m-V2t）;

D=

-Rsin（θm+θt）cosθm（V2m-V2t）at。

令期望的攻击时间为Td， 则可定义滑模面（即攻击时间误差）：

St=t+tgo3-Td（23）

对滑模面St求导可得

S·t=1+t·go3=1+F+Bam+D（24）

式中： D包含有目标的加速度和前置角等信息， 在实际作战过程中， 包含目标运动信息的状态通常不易被精确获得， 这也就意味着式（22）中的D为未知量， 令x=tgo3+t， 则基于非线性扰动观测器可设计制导律如下：

am=-F+1+D^+k1St+k2sgnγ（St）B

D^=ω+k0x

ω·=-k0ω-k0（1+F+Bam+k0x）（25）

式中： k1和k2为制导律中大于0的待设计的常数; k0为扰动观测器中的待设计常数。

证明： 首先， 定义观测器跟踪误差D～=D-D^， 假设系统扰动D·有界， 满足D·≤β， 选择李雅普诺夫函数V2：

V2=12S2t+12D～2（26）

对V2求导可得

V·2=StS·t+D～D～·=St（1+F+Bam+D）+D～D～·=St（-k1St-k2sgnγ（St）+D-D^）+D～D～·=-k1S2t-k2Stγ+1+StD～+D～D～·（27）

且

D～D～·=D～（D·-D^·）=D～（D·-ω·-k0x·） （28）

根据观测器定义可知：

ω·+k0x·=-k0ω-k0（1+F+Bam+k0x）+

k0（1+F+Bam+D）=-k0ω-k0x2+k0D=

-k0（ω+k0x）+k0D=-k0D^+k0D=k0D～ （29）

将式（29）代入式（28）可得

D～D～·=D～（D·-D^·）=D～（D·-ω·-k0x·）=

D～（D·-k0D～）=-k0D～2+D～D·≤-k0D～2+12D～2+12β2≤-k0-12D～2+12β2（30）

进一步， 将式（30）代入式（27）可得

V·2=-k1S2t-k2Stγ+1+StD～+D～D～·≤

-k1S2t-k2Stγ+1+12S2t+12D～2-

k0-12D～2+12β2≤-k1-12S2t-

（k0-1）D～2+12β2≤-αV2+σ（31）

式中： α=min2k1-12， 2（k0-1）; σ=12β2。

由式（31）和引理4可得， 系统是实际有限时间收敛的， 至此， 制导律式（25）稳定性得证。

虽然tgo3的推导仍是基于目标机动为0且导弹前置角为常值下得到的， 当目标机动时， 这无疑将会引入估计误差， 但在稍后的仿真分析中可以看出， 式（25）仍然可以保证导弹以期望的攻击时间拦截目标。

3 仿真分析

3.1 协同比例制导律仿真分析

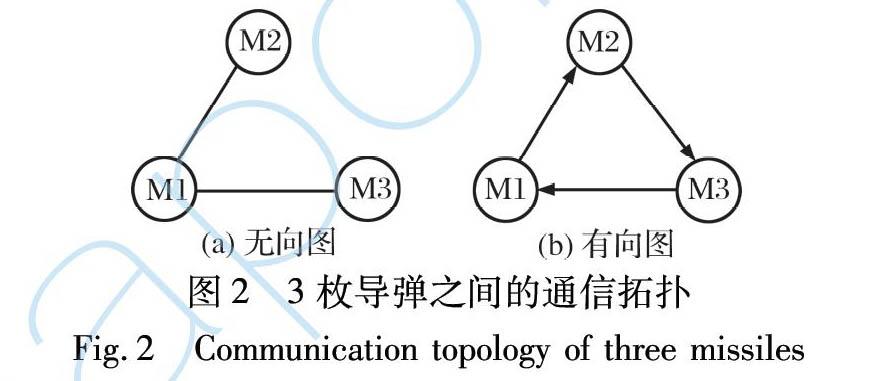
首先对所设计的基于比例加偏置项的时间协同制导律进行仿真验证。 以3枚导弹拦截1个机动目标为例， 仿真初始参数设置如表1所示， 3枚导弹之间的通信网络如图2所示， 分别给出导弹通信拓扑为无向和有向的情形。 选择目标以余弦机动at=5gcosπt2的情况进行仿真， 并以比例导引作为对比， 对所设计的制导律进行验证。 导弹仿真初始参数为： Ni=3; k11=2.8; k12=2.5; k13=2.6; k21=k22=k23=1.2。 無向图和有向图的通信矩阵分别为： C无向=011100100; C有向=001100010。

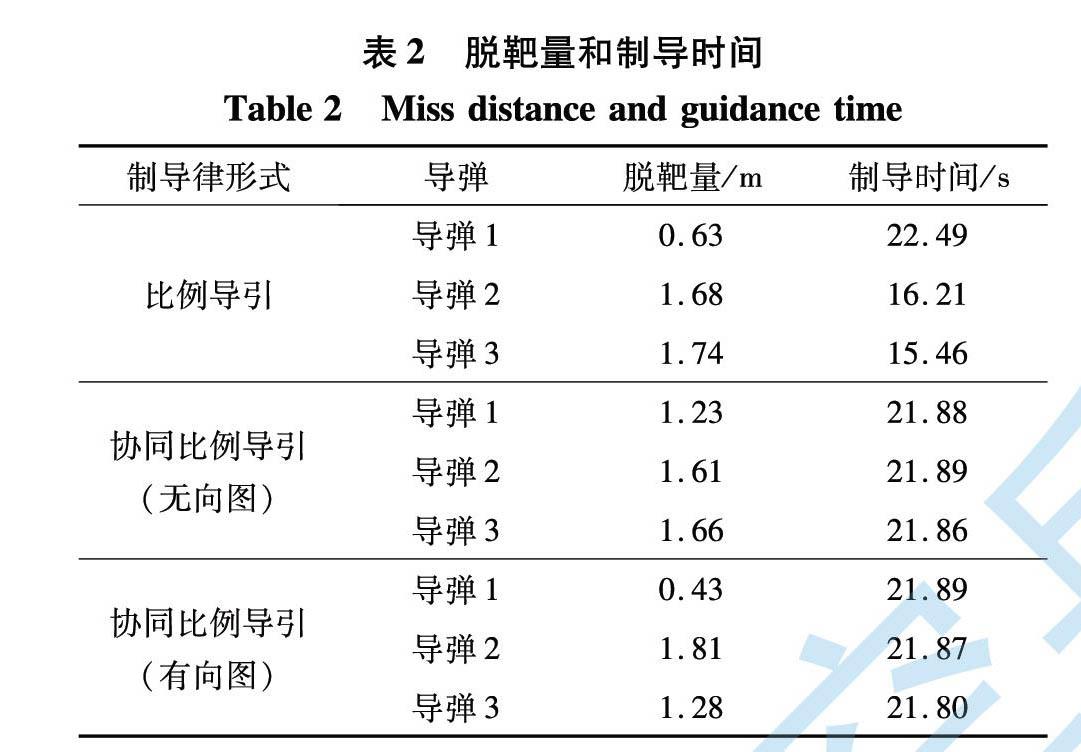
仿真结果如图3所示。 其中脱靶量和制导时间如表2所示。

导弹31.2821.80图3给出了所设计的协同比例制导律和传统比例制导律之间的仿真对比。 图3（a）～（c）为比例导引和在有向和无向图下协同比例导引的弹目运动轨迹， 可知， 所设计的协同制导律可以保证3枚导弹同时命中目标。 图3（d）～（f）为导弹剩余飞行时间的变化曲线， 可知， 协同比例制导律可以纠正较大的初始飞行时间误差， 并保持较高的精度收敛。 图3（g）～（i）为协同制导律中导弹过载的变化曲线， 可知， 相比比例导引， 协同制导律在初始阶段需要较大的加速度来调整攻击时间误差。 图3（j）～（l）为协同制导律的导航系数的变化曲线， 可知， 不同的通信拓扑下， 导弹的导航系数变化趋势不同， 但最后随着剩余飞行时间的收敛， 导航系数也将收敛。

注3： 协同比例制导律的核心是调整比例导引的导航系数， 进而调整各导弹的攻击弹道， 实现协同攻击。 仿真结果证明所设计的协同制导律对于机动目标仍能以较高的精度实现协同打击。 虽然在协同比例制导律中采用的tgo1是基于静止目标假设推导出来的， 但在制导律的设计过程中， 并没有用tgo1来控制导弹实际的飞行时间， 而是将目标在每个时刻视为静止的点， 将每枚导弹的剩余飞行时间视为协调变量， 来动态调节各自的导航比。 随着导弹与目标相对距离的减小， tgo1的估计误差也越来越小， 从而实现对机动目标的协同打击。

3.2 指定攻击时间制导律仿真分析

对基于tgo3所设计的指定攻击时间协同制导律进行仿真分析。 以单枚导弹攻击机动目标场景为例， 导弹的仿真初始条件如表3所示。 在传统比例制导律下的仿真结果如图4所示。

由图4可以看出， 在传统比例制导律下， 导弹攻击时间为20.46 s。 为了验证所设计的指定攻击时间制导律， 分别选择Td=21 s， Td=22 s， Td=23 s三种场景进行仿真验证。 仿真初始参数如下：

Td=21 s时， [k1， k2]=[1.7×10-6， 1.8×10-5]×R;

Td=22 s时， [k1， k2]=[2×10-6， 3.6×10-5]×R;

Td=23 s时， [k1， k2]=[3×10-6， 2.3×10-5]×R;

k0=10， γ=0.9。 仿真结果如表4所示。

图5给出了所设计的指定攻击时间控制制导律的仿真结果。

由图5可知， 所设计的制导律可以保证导弹以期望的攻击时间攻击目标。 图5（c）为弹目相对距离的变化， 可以看出， 在不同的攻击时间下， 导弹仍能以较高的精度打击目标。 图5（d）～（f）为不同的Td下， 所设计的扰动观测器的估计结果， 可以看出， 所设计的观测器可以较好地跟踪系统扰动。 图5（g）～（i）为导弹过载的变化曲线， 可以看出， 过载在末制导过程中会发生抖振， 这主要是因为本文所使用的tgo3未考虑目标的机动， 这无疑会引起tgo3的估计误差， 进而在制导末期造成滑模面的抖振问题。

为进一步验证所设计制导律的有效性， 考虑3枚导弹攻击机动目标的场景。 仿真的初始参数如表5所示。 仿真结果如图6所示， 脱靶量和制导时间如表6所示。

图6给出了所设计的指定攻击时间制导律协同攻击某机动目标的仿真结果。 图6（a）～（d）为导弹在比例导引和本文所设计的指定攻击时间制导律下的弹道图和弹目相对距离变化图， 可以看出， 所设计的制导律可以保证各导弹以期望的攻击时间依次打击目标， 这在攻击一些战机等目标的场景中具有重要意义。 图6（e）为指定攻击时间制导律的剩余飞行时间变化曲线。 图6（f）为3枚导弹的过载变化曲线。

注4： 与常规比例导引相比， 所设计的指定攻击时间制导律弹道更加弯曲， 这是因为指定的攻击时间较比例导引所需时间更长， 需要导弹进行额外的机动来调整攻击时间。 虽然该制导律所采用的tgo3是基于目标不机动、 导弹前置角为常值下的条件推导的， 但是相比于tgo1， tgo3的推导是基于导弹和目标的相对运动学方程得到的， 且没有用到任何近似条件。 当目标机动时， 将目标机动带来的影响视为扰动， 以此来实现对导弹攻击时间的控制。 需要注意的是， 由于tgo3估计误差的存在， 在制导末期会造成滑模面的抖振问题。 下一步工作中， 将致力于解决导弹过载的抖振问题。

注5： 实质上， 本文所设计的两种不同制导律， 其根本区别在于协同比例制导律是通过建立导弹的剩余飞行时间与导航系数之间的关系， 利用导航系数改变导弹弹道特性的特点， 通过网络通信在线调整剩余飞行时间， 进而实现协同攻击; 而指定攻击时间制导律则主要是利用tgo3的动力学特性， 通过设计导弹加速度， 离线的改变导弹的剩余飞行时间， 从而实现对目标的同时或依次攻击。 虽然两种制导律的作用机理和制导体制不同， 但仿真分析证明， 这两种制导律都能有效针对机动目标， 实现对机动目标的协同攻击。

4 结  论

本文针对多导弹协同拦截机动目标的问题， 从剩余飞行时间控制的角度出发， 通过对三种常用的剩余飞行时间形式的分析， 总结并梳理了不同剩余飞行时间形式的局限性和优越点。 分别基于在线调整导航系数和离线设计剩余飞行时间的思想设计了分布式协同比例制导律和具有指定攻击时间控制的滑模制导律， 并给出严谨的理论证明与仿真分析。 通过与传统的比例导引进行对比， 验证了本文所设计的制导律的有效性。 在下一阶段， 本文将针对具有较大初始偏差下， 综合考虑导弹的视场角约束、 攻击角约束及过载约束等条件， 设计多约束条件下的协同制导律。

参考文献：

[1] Jeon I S，  Lee J I，  Tahk M J. Impact-Time-Control Guidance Law for Anti-Ship Missiles[J]. IEEE Transactions on Control Systems Technology，  2006，  14（2）： 260-266.

[2] Lee J I，  Jeon I S，  Tahk M J. Guidance Law to Control Impact Time and Angle[J]. IEEE Transactions on Aerospace and Electronic Systems，  2007，  43（1）： 301-310.

[3] Jeon I S，  Lee J I，  Tahk M J. Homing Guidance Law for Cooperative Attack of Multiple Missiles[J]. Journal of Guidance，  Control，  and Dynamics，  2010，  33（1）： 275-280.

[4] Cho D，  Kim H J，  Tahk M J. Nonsingular Sliding Mode Guidance for Impact Time Control[J]. Journal of Guidance，  Control，  and Dynamics，  2015，  39（1）： 61-68.

[5] Kumar S R，  Ghose D. Sliding Mode Control Based Guidance Law with Impact Time Constraints[C]∥American Control Conference，  2013： 5760-5765.

[6] 洪超，  夏群利，  阮聰. 带视场角约束的多弹三维协同制导律[J]. 战术导弹技术，  2020（6）： 37-43.

Hong Chao，  Xia Qunli，  Ruan Cong. Multi-Missile Three-Dimensional Cooperative Guidance Law with Field-of-View Constraint[J]. Tactical Missile Technology，  2020（6）： 37-43.（in Chinese）

[7] 张振林，  张科，  郭正玉，  等. 一种新型领从式多弹协同制导律设计[J]. 航空兵器，  2020，  27（5）： 33-38.

Zhang Zhenlin，  Zhang Ke，  Guo Zhengyu，  et al. Design of a New Guidance Law for Guided Multiple Missiles[J]. Aero Weaponry，  2020，  27（5）： 33-38.（in Chinese）

[8] Sinha A，  Kumar S R. Supertwisting Control-Based Cooperative Salvo Guidance Using Leader-Follower Approach[J]. IEEE Transactions on Aerospace and Electronic Systems，  2020，  56（5）： 3556-3565.

[9] 花文涛，  刘沛文，  贾晓洪，  等. 一种多弹协同制导策略[J]. 兵器装备工程学报，  2021，  42（2）： 180-183.

Hua Wentao，  Liu Peiwen，  Jia Xiaohong，  et al. Multi-Missile Co-operative Attacking Strategy[J]. Journal of Ordnance Equipment Engineering，  2021，  42（2）： 180-183.（in Chinese）

[10] Yu J L，  Dong X W，  Li Q D，  et al. Cooperative Guidance Strategy for Multiple Hypersonic Gliding Vehicles System[J]. Chinese Journal of Aeronautics，  2020，  33（3）： 990-1005.

[11] 钟泽南，  赵恩娇，  赵新华，  等. 基于固定时间收敛的攻击时间控制协同制导律[J]. 战术导弹技术，  2020（6）： 30-36.

Zhong Zenan，  Zhao Enjiao，  Zhao Xinhua，  et al. Impact Time Control Cooperative Guidance Law Based on Fixed-Time Convergent[J]. Tactical Missile Technology，  2020（6）： 30-36.（in Chinese）

[12] 花文华，  张拥军，  张金鹏，  等. 多导弹攻击时间协同的滑模制导律[J]. 中国惯性技术学报，  2018，  26（1）： 98-102.

Hua Wenhua，  Zhang Yongjun，  Zhang Jinpeng，  et al. Sliding-Mode Guidance Law for Attack Time Cooperation of Multi-Missiles[J]. Journal of Chinese Inertial Technology，  2018，  26（1）： 98-102.（in Chinese）

[13] Zhao J，  Zhou R. Unified Approach to Cooperative Guidance Laws Against Stationary and Maneuvering Targets[J]. Nonlinear Dynamics，  2015，  81（4）： 1635-1647.

[14] Kumar S R，  Mukherjee D. Terminal Time-Constrained Nonlinear Interception Strategies Against Maneuvering Targets[J]. Journal of Guidance，  Control，  and Dynamics，  2020，  44（1）： 200-209.

[15] 宋俊红，  宋申民，  徐胜利. 一种拦截机动目标的多导弹协同制导律[J]. 宇航学报，  2016，  37（12）： 1306-1314.

Song Junhong，  Song Shenmin，  Xu Shengli. A Cooperative Gui-dance Law for Multiple Missiles to Intercept Maneuvering Target[J]. Journal of Astronautics，  2016，  37（12）： 1306-1314.（in Chinese）

[16] 郭正玉，  王超磊，  錢航，  等. 带有攻击角约束的大机动目标协同攻击制导律[J]. 西北工业大学学报，  2020，  38（6）： 1257-1265.

Guo Zhengyu，  Wang Chaolei，  Qian Hang，  et al. Cooperative Intercepting Guidance Law for Large Maneuvering Target with Impact Angle Constraint[J]. Journal of Northwestern Polytechnical University，  2020，  38（6）： 1257-1265.（in Chinese）

[17] Zhao Q L，  Dong X W，  Song X，  et al. Cooperative Time-Varying Formation Guidance for Leader-Following Missiles to Intercept a Maneuvering Target with Switching Topologies[J]. Nonlinear Dynamics，  2019，  95（1）： 129-141.

[18] Chen Z Y，  Yu J L，  Dong X W，  et al. Three-Dimensional Coopera-tive Guidance Strategy and Guidance Law for Intercepting Highly Maneuvering Target[J]. Chinese Journal of Aeronautics，  2021，  34（5）： 485-495.

[19] Ren W，  Beard R W，  Atkins E M. Information Consensus in Mult-ivehicle Cooperative Control[J]. IEEE Control Systems Magazine，  2007，  27（2）： 71-82.

[20] Olfati-Saber R，  Murray R M. Consensus Problems in Networks of Agents with Switching Topology and Time-Delays[J]. IEEE Transactions on Automatic Control，  2004，  49（9）： 1520-1533.

[21] Yu S H，  Yu X H，  Stonier R. Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Modes[C]∥ Proceedings of the Sixth International Conference of Information Fusion，  2003： 1433-1440.

[22] Zhu Z，  Xia Y Q，  Fu M Y. Attitude Stabilization of Rigid Spacecraft with Finite-Time Convergence[J]. International Journal of Robust and Nonlinear Control，  2011，  21（6）： 686-702.

[23] Zhou J L，  Yang J Y. Distributed Guidance Law Design for Coopera-tive Simultaneous Attacks with Multiple Missiles[J]. Journal of Guidance，  Control，  and Dynamics，  2016，  39（10）： 2436-2445.

Multi-Missile Cooperative Guidance Law for

Intercepting Maneuvering Target

Ma Mengchen，  Song Shenmin*

（Center for Control Theory and Guidance Technology，  Harbin Institute of Technology， Harbin 150001， China）

Abstract： Aiming at the problem of multi-missile cooperative interception of maneuvering targets，  two different cooperative guidance laws are designed based on the time-to-go. For the scenario of multi-missile distributed communication， a distributed cooperative proportional guidance law with time-varying navigation coefficients is designed based on the idea of biased proportional guidance. For the scenario of specified attack time，  based on the form of time-to-go under constant lead angle，  a sliding mode guidance law with a specified attack time is designed by using sliding mode control and nonlinear disturbance observer. Simulation results show that the two guidance laws proposed in this paper can effectively carry out cooperative attack or sequential attack against maneuvering targets.

Key words：  maneuvering target; time-to-go; biased proportional navigation; nonlinear disturbance observer; sliding mode control; multi-missile cooperation; guidance law