高中物理“氢原子光谱与玻尔模型”的教学尝试

鲁 斌

(浙江省余姚中学 浙江 宁波 315400)

1 引言

“氢原子光谱与玻尔模型”的内容，在人教版《物理·选修3-5》[1]教材中，分两节展开.第十八章第3节“氢原子光谱”中，介绍了光谱及光谱的分类、氢原子光谱的实验规律、经典理论的困难；在第4节“玻尔的原子模型”中，介绍了玻尔原子理论的基本假设、玻尔理论对氢光谱的解释、玻尔模型的局限性.笔者尝试，将两节内容合并为一节，先展现氢原子光谱的实验现象，再引入玻尔理论进行解释，使整堂课的结构更加完整.在此过程中，也应处理和考虑以下问题：

(1)突出主线，弱化对光谱分类、作用等相关内容的讨论.

(2)实验展示氢原子光谱的谱线.

(3)补充光栅方程、分光计等相关内容，定量测量氢原子光谱.

(4)比较自然地得到巴尔末公式.

(5)为巴尔末公式与玻尔理论搭建桥梁.

(6)补充角动量等内容，将玻尔理论的基本假设进行完备.

(7)推导里德伯公式，验证玻尔理论.

2 光谱

2.1 光谱的呈现

实验1：太阳光谱

用三棱镜展示太阳光谱.配合讲解：1665年，牛顿就发现了白光通过三棱镜后能够得到绚丽的光带，并把实验中得到的彩色光带叫做光谱.炽热的固体、液体、高压的气体的光谱，是由连续分布的一切波长的光组成的，这种光谱叫做连续光谱.

提问：是否所有物体发出的光谱都是连续谱？

实验2：钠的焰色反应

将蘸有食盐水的细铁丝放置于酒精灯的灯焰上，看到黄色的火焰，这就是化学课中提到的焰色反应.课件展示钠元素的光谱线，两条钠黄双线(图1)非常明锐.

图1 钠黄双线

师：只含有一些不连续的亮线的光谱叫明线光谱(线状谱).明线光谱中的亮线叫谱线，各条谱线对应不同波长的光.

实验3：光谱管组(图2)实验

图2 光谱管组

利用光谱管组，展示氢气、氮气、氩气、氦气、氖气、汞蒸气的放电现象.

由于每种原子都有自己的特征谱线，因此可以根据光谱来鉴别物质和确定的化学组成，这种方法叫做光谱分析.

课件展示元素的光谱线，如图3所示.

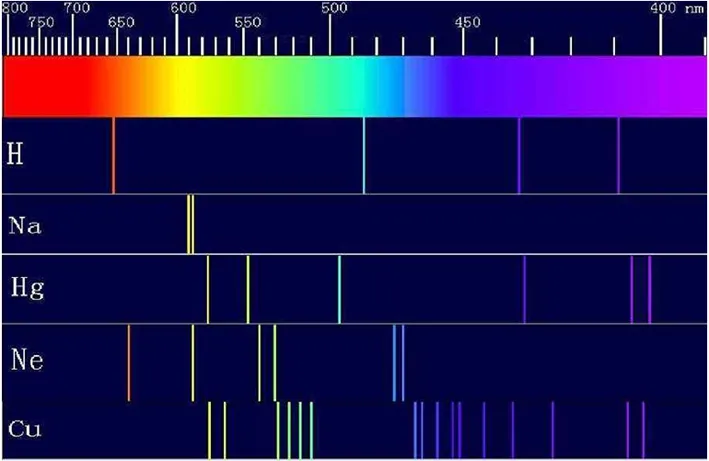
图3 连续谱与线状谱

我们得到了大量元素的谱线，并要对其进行研究、解释.由于氢原子具有最简单的结构，我们就从氢原子产生的光谱入手.

2.2 观察氢原子光谱

实验4：利用分光计观察氢原子光谱

调平分光计，将三棱镜放置于载物台上，点亮氢灯，实验装置图如图4所示.

图4 用分光计观察氢原子光谱

在望远镜处观察经过三棱镜折射的氢原子光谱如图5所示.

图5 氢原子光谱中的红色与绿色谱线

通过三棱镜我们观察到了4条分立的谱线：红色、绿色、紫色、淡紫色.

提问：这些光谱的波长为多少呢？

2.3 测量谱线波长

实验5：利用光栅测量氢原子光谱

由大量等宽等间距的平行狭缝构成的光学器件称为光栅.一般常用的光栅是在玻璃片上刻出大量平行刻痕制成，刻痕为不透光部分b，两刻痕之间的透光部分为a，相当于一狭缝.本次实验采用的光栅为1 mm刻600条线，光栅常数定义为

如图6所示，当平行光入射时，相邻透光部分的光程差为dsinθ，容易证明，当光程差满足

图6 光栅衍射光路图

dsinθ=kλ

(1)

式中k为整数，即可在P处产生明纹.

我们选取绿色光谱进行测量.其光栅的一级衍射角为16°55′，代入式(1)，得到绿色光谱的波长为485.2 nm.通过相同的计算方法，我们可以得到氢原子光谱的其他谱线波长,如图7所示,并分别标记为Hα,Hβ,Hγ,Hδ.

图7 氢原子谱线波长

提问：从这些波长分布中，你能发现什么规律吗？

这看似是一个数学游戏，却包含着深刻的物理内涵.

3 巴尔末公式与里德伯常数

3.1 巴尔末的数学游戏

瑞士数学教师巴尔末也一直在研究这个问题，1885年，他发现了一个非常重要的公共因子[2]：364.6 nm,如果将氢原子的波长除以这个数，就会得到如下结果,如图8所示

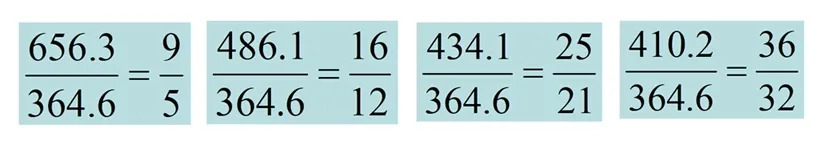
图8 呈现的计算结果

提问：你能从这些数据中得到它们满足的规律吗？

我们可以得到

(2)

式(2)即为巴尔末公式.

当然我们可以将公式进行处理

(3)

这个公式是否正确，需要通过实验进行检验，我们将n=7代入公式，算出了一条λ=397.0 nm的谱线，通过实验观察，果然观察到了这条谱线Hε，其波长为397.1 nm.

提问：巴尔末公式可以较好地解释氢原子光谱，那么公式背后的物理又是什么呢？我们怎么去理解这个公式？

3.2 里兹和里德伯

这时候出现了两个非常重要的物理学家，一位是瑞典物理学家、数学家里德伯，一位是瑞士理论物理学家里兹.

他们试着将公式倒过来，则式(3)为

则公式可总结为

(4)

提问：从这个公式中，我们能得到什么启发吗？

让我们仔细来端详这个公式[3]:

(1)包含两项.说明原子发光过程牵涉到两个对象，有初项与末项，即初态与末态.

(2)差值.两项由减号连接，这要求他们一定对应同一物理性质的不同状态，两者的落差决定发光的波长特征.这是一个类似“跳楼”的过程.

(3)整数平方.这个物理性质的数值要正比于整数平方的倒数.

如果我们能找到一个模型，且其满足上述3个要求的话，说不定能解释氢原子的发光.

4 玻尔理论及其解释

还记得此前普朗克和爱因斯坦已经确立了光能量量子的概念吗？此能量正比于光的频率，ε=hν把式(4)改写为

一切都变得豁然开朗了,氢原子里只有电子和质子，变化的是电子相对于质子的运动.如果电子的能量是个正比于整数平方倒数的量，电子从一个较高能量的状态跳跃(jump)到一个较低能量的状态，因为能量要守恒，假设能量差对应发射光的能量量子，则氢原子光谱的特征就能得到解释.

1913年，年轻的丹麦人玻尔就是这么想的.为了解释氢原子光谱，他提出了3条基本假设.

4.1 定态假设

假设氢原子中，电子绕着原子核做圆周运动，库仑力提供电子做圆周运动的向心力.按照经典物理学，电子做圆周运动属于变加速运动，会辐射电磁波损耗能量，因此电子绕核转动这个系统是不稳定的，电子会失去能量，最后一头栽到原子核上(图9)，但事实不是这样，原子是个很稳定的系统.

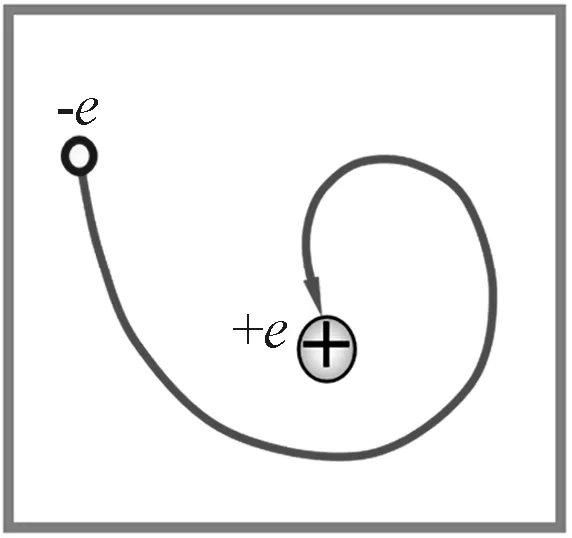
图9 不稳定的轨道

为了解决这个问题，玻尔提出了“定态假设”.原子中的电子只能在一些半径不连续的轨道上(图10)做圆周运动.在这些轨道上运动的电子不辐射(或吸收)能量而处于稳定状态，称为“定态”.

图10 定态轨道

假设电子只能在定态轨道r1，r2，…，rm，rn运动，则电子的环绕规律为

(5)

4.2 频率条件假设

光辐射是怎么产生的呢？

由于每个轨道都对应有不同的能量，电子从某一定态向另一定态跃迁时将发射(或吸收)光子.若电子在轨道rn处的能量为En，在轨道rm处的能量为Em，从轨道rn向rm跃迁时，能放出频率为ν的光子(图11)，满足

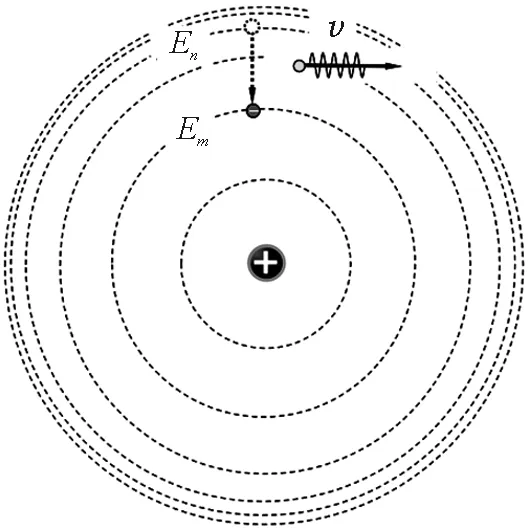
图11 跃迁

ε=hν=En-Em

(6)

4.3 角动量量子化条件假设

那么，能量为什么会分立呢？

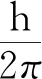
图12 角动量量子化

(7)

此为角动量量子化假设.

4.4 理论求解

根据以上假设，我们如何解释氢原子光谱的规律呢？

联立式(5)、式(7)，消去vn，得到

(8)

可见，轨道是量子化的.电子在定态轨道上的机械能为

(9)

将式(8)代入式(9)

(10)

为了得到巴尔末公式与里德伯常数，则

(11)

令n=2，即可得到巴尔末公式，里德伯常数的理论值与实验值几乎一致.由此也成功解释了氢原子光谱.

4.5 玻尔理论的局限性

至此，氢原子光谱有了合理的解释.科学的发展离不开一代又一代人的努力.然而，玻尔理论真的正确吗？

玻尔理论成功地解释并预言了氢原子辐射的电磁波的问题，但是也有它的局限性.玻尔理论在解决核外电子的运动时成功引入了量子化的观念，同时又应用了“粒子、轨道”等经典概念和有关牛顿力学规律.除了氢原子光谱外，在解决其他问题上遇到了很大的困难，例如氦原子光谱.为什么电子要在定态的轨道上运动呢？为什么定态轨道上不会辐射电磁波呢？为什么要求角动量一定是普朗克常数的整数倍呢？为什么电子会像行星一样限制在一个平面内运动呢？物理模型在解决一些问题的同时总会带来新的问题.

5 结束语

本堂课通过对氢原子光谱的研究，从实验现象和理论解释入手，试图还原历史发展的脉络，力图展现科学探究过程中的偶然性与必然性.对于高中学生而言，从高考层面，只要能够利用能级差计算光子频率即可.对于氢原子光谱的产生、测量、玻尔理论涉及的具体内容和数学推导并不要求.但从核心素养层面，经历实验探究，培育科学思维，是物理课堂的重要使命.在此之后，大师辈出，薛定谔、海森伯、泡利、费米、德布罗意、狄拉克、波恩等等科学家前赴后继，逐步发展和完善量子力学的框架，才有现在的信息社会.