无限长载流薄板磁场的矢势与磁感应强度计算及可视化*
2021-01-06周群益
周群益
(广州理工学院 广东 广州 510540)
莫云飞
(长沙学院电子信息与电气工程学院 湖南 长沙 410022)
周丽丽
(赣南医学院信息工程学院 江西 赣州 341000)
侯兆阳
(长安大学理学院应用物理系 陕西 西安 710064)
1 引言
求无限长均匀通电薄板的磁场是电磁场理论中的一个典型习题,一般教材只计算中垂面或(和)板平面上的磁感应强度[1],有的习题解答计算了全部空间的磁感应强度[2,3],其根据是无限长直线电流的磁感应强度公式和场强叠加原理.但这些教材和习题解答没有图像,也没有对结果进行分析.本文根据无限长直线电流磁场的矢势公式和矢势叠加原理求薄板电流磁场的矢势,再利用磁感应强度与矢势的关系简单地求出磁感应强度,并将公式无量纲化,计算和绘制了矢势和磁感应强度的分布曲面以及二维磁感应线,充分显示了磁场的分布规律.
2 薄板电流磁场的矢势
无限长直导线通有电流I,其磁场矢势的方向与电流方向相同,大小为[4]
(1)
其中,R是场点到直线电流的距离,R0是矢势零点到直线电流的距离.
设薄板的宽度为2L,电流为I,则面电流的线密度
如图1所示,在直角坐标系Oxyz中电流方向沿着z方向(垂直纸面向外),矢势A和磁感应强度B的分布与坐标z无关.

图1 无限长通电薄板的截面和磁场的矢势
取Oxy截面,在距离为l处取长度dl,那么,电流元为
dI=jdl
场点P(x,y)到电流元dI的距离为
(2)
电流元在点P产生磁场的矢势大小为
薄板电流在点P产生磁场的矢势大小为
(3)
利用分部积分法可得
2y(arctank2-arctank1) + 4L+ 4LlnR0]
(4)
其中
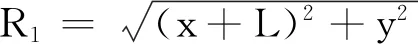
(5)
(6)
这里,R2和R1分别是场点P到薄板右端和左端的距离,k2和k1分别是角度θ2和θ1的正切.取(0,0)为矢势零点,可得
lnR0=lnL-1
(7)
因此
(8)
当x=0时,可得中垂面上的矢势大小
(9)
当y→0时,可得板平面上的矢势大小
(10)
当x=0时,可得原点处的矢势A(0,0) = 0.
3 薄板电流的磁感应强度
根据矢势的旋度可求磁感应强度
B=▽×A
(11)
在直角坐标系中可得
分量为
(12)
将式(4)代入上式,可得磁感应强度的两个分量
(13)
(14)
合磁感应强度大小为
(15)
方向由角度确定
(16)
讨论:(1)当x= 0时,由式(13)、(14)可得中垂面上磁感应强度的两个分量
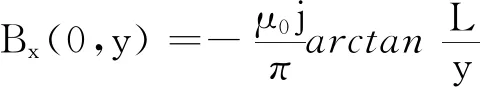
(17)
当y→±0时,可得原点处的磁感应强度
(18)
(2)当y→0时,由式(13)、(14)可得板平面上磁感应强度的两个分量

(19)
(20)
(3)当L→∞时,由式(13)可得

(21)
由式(14)可得
(22)
说明无限大薄板电流在两边产生的是匀强磁场.
(4)当|x|≫L且|y|≫L时,由式(13)可得
(23)
由式(5)可得
将R1和R2代入式(14),可得
(24)
将Bx和By代入式(15),可得
(25)
这是无限长直线电流产生的磁感应强度公式.
4 磁场公式的无量纲化
取L作为坐标单位,则
二者均为无量纲的坐标.取
为矢势的单位,将式(7)代入式(1),可得直线电流磁场的无量纲的矢势
(26)
其中
薄板电流磁场的无量纲的矢势为
arctank2-arctank1)
(27)
其中

(28)
(29)
同理可得中垂面和板平面上无量纲的矢势.
设
显然
取B0作为磁感应强度的单位,则无量纲的磁感应强度分量分别为
(30)
(31)
无量纲的合磁场大小和方向分别为
(32)
同理可得中垂面和板平面上无量纲的矢势和磁感应强度的分量.
5 磁场的可视化
(1)无限长薄板电流在中垂面上磁场的矢势Az(0,y)的曲线如图2(a)所示,Az(0,y)是y的偶函数,离板越近,矢势越高,y= 0处是一个尖点;当|y|很大时,其矢势接近于直线电流磁场的矢势.中垂面上的磁场Bx(0,y)的曲线如图2(b)所示,中垂面上的磁场分量By(0,y)=0,而分量Bx(0,y)是y的奇函数,说明薄板两边磁场的方向相反,离板越近,磁场越大.磁场在y=0处发生跳跃,这是因为Az(0,y)在此处是尖点.当|y|很大时,其磁场接近于直线电流产生的磁场.

图2 无限长均匀通电薄板中垂面上的矢势和磁场
(2)薄板电流在板平面磁场的矢势Az(x,0)的曲线如图3(a)所示,Az(x,0)是x的偶函数,轴心的矢势最高;在板的边缘x=±L处的矢势是拐点,当|x|很大时,其矢势接近于直线电流磁场的矢势.板平面上的磁场By(x,0)的曲线如图3(b)所示,By(x,0)是x的奇函数,板内磁场是单调上升的曲线,板外磁场是单调下降的曲线,板的边缘x=±L处的磁场在理论上是无穷大;当|x|很大时,其磁场接近于直线电流产生的磁场.
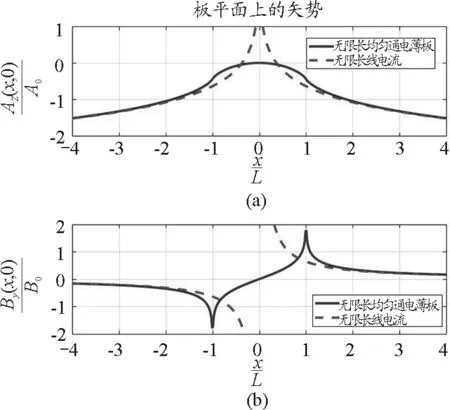
图3 无限长均匀通电薄板平面上的矢势和磁场
(3)薄板电流磁场的矢势Az(x,y)分布面如图4所示,点(0,0)的矢势最高;中垂面上的矢势Az(0,y)的曲线和板平面上的矢势Az(x,0)的曲线分布在曲面上.
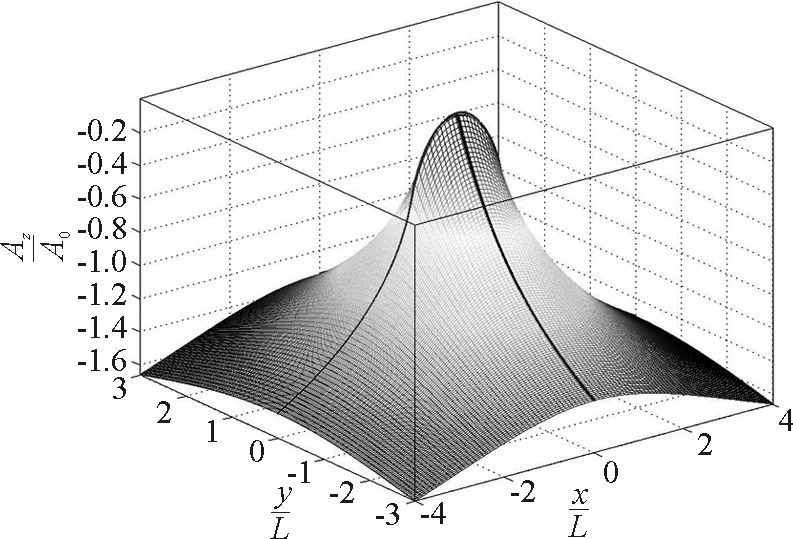
图4 无限长均匀通电薄板磁场的矢势分布面
(4)薄板电流磁场的x分量Bx(x,y)的曲面如图5所示,Bx有一个“峭壁”,位于薄板所在处,在板的表面(x,0+),磁场为-B0;在板的表面(x,0-),磁场为B0.
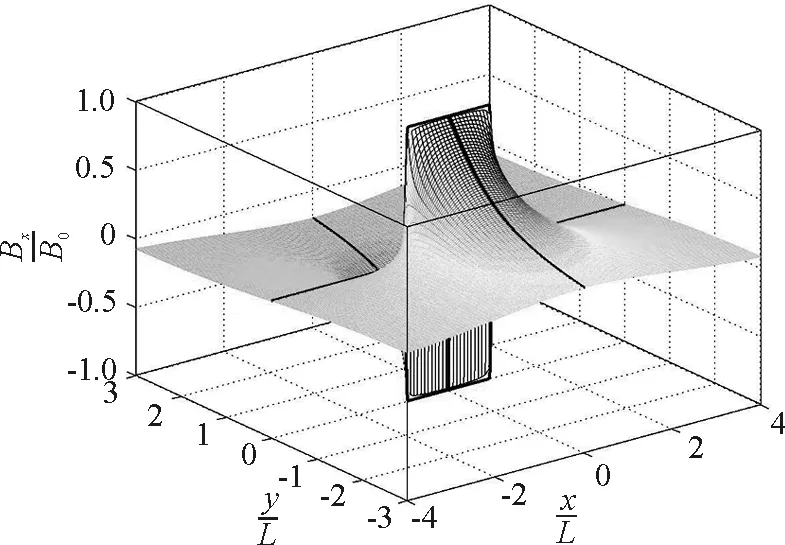
图5 无限长均匀通电薄板磁场的x分量分布面
(5)薄板电流磁场的y分量By(x,y)的曲面如图6所示,By有一对对称的“峰”和“谷”,这是薄板边缘的By,(±L,0)处的By在理论上是无穷大.
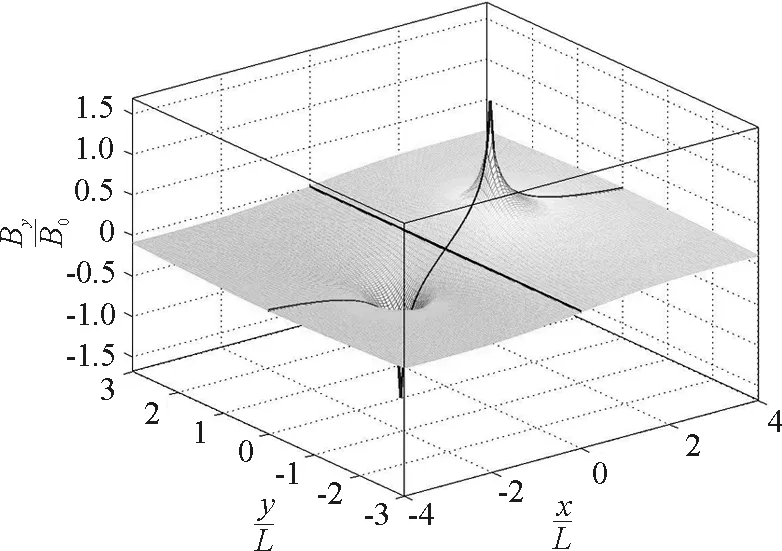
图6 无限长均匀通电薄板磁场的y分量分布面
(6)合磁场B(x,y)的曲面如图7所示,点(0,0)是B的一个鞍点.B有一对犄角,说明薄板边缘的磁场在理论上是无穷大.
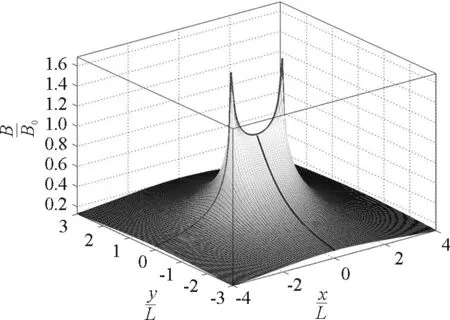
图7 无限长均匀通电薄板合磁场的分布面
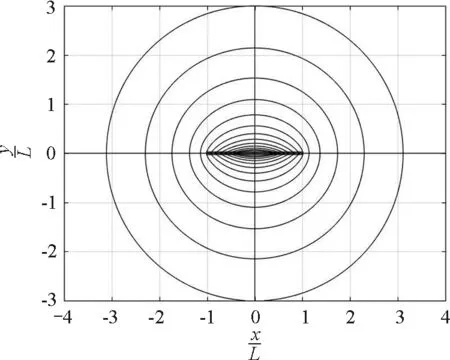
(7)合磁场B的方向角α(x,y)曲面如图8所示,α随着极角的增加而增加.在x=0,y>0的正轴上,α发生从π到-π的跃变;在y= 0,-L 图8 无限长均匀通电薄板磁场方向的分布面 (8)薄板电流磁场在截面上的磁感应线如图9所示,在薄板附近,磁感应线比较密集,磁场比较强;离板越远,磁感应线越稀疏,磁场越弱;远处的磁感应线接近于圆. 图9 无限长均匀通电薄板的磁感应线 本文建立了均匀通电薄板在直角坐标系中的矢势和磁感应强度公式,通过无量纲化处理,解决了有关的计算和可视化的问题.如果将这种方法解决均匀带电薄板的电势和电场强度的问题,将发现两个问题的解答和图片有许多相似之处.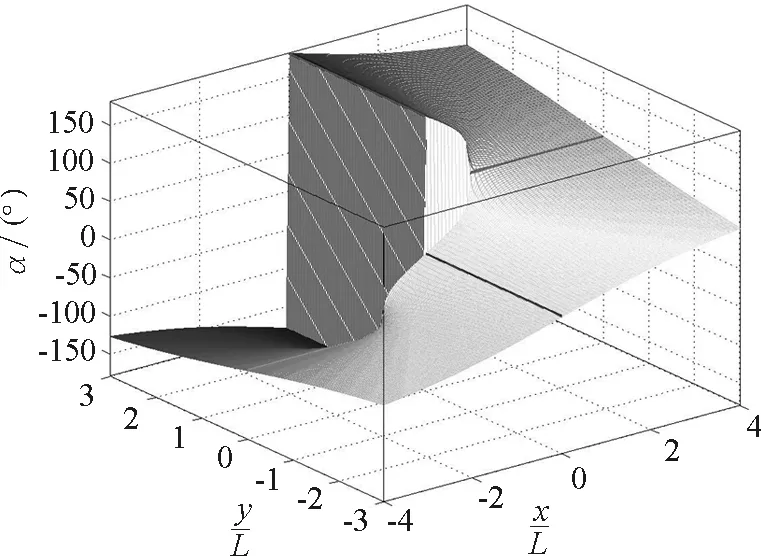
6 结束语
