NaAs材料分子R线系高激发量子态跃迁谱线研究

胡处平，樊群超，付　佳，詹　杰，张春国(西华大学理学院，高性能科学计算重点实验室，四川 成都　610039)

获得分子精确的跃迁谱线是现代材料科学的重要研究内容之一,尤其是高激发量子态的跃迁谱线数据在研究分子精确的内部结构时(如获得高分辨率光谱从而对分子结构和性能进行精确分析[1-2]等)具有非常重要的作用和应用价值。同时，精确的跃迁谱线在星际分子观测与研究、天体物理研究、大气化学的成分分析等方面都有重要的应用价值[3-5]。近年来，人们投入大量的精力对跃迁谱线进行了广泛深入的研究[6-7]。实验上出现了许多好的研究方法，如光外差磁旋转速度调制光谱技术[8]、光腔衰荡光谱技术[9]等来直接观测体系的跃迁谱线，这些方法对于研究低激发量子态谱线结构是十分有效的，而对于高激发量子振转态，由于受实验设备自身条件的约束，获得这部分区域的精确光谱数据仍然十分困难。另一方面，人们试图通过理论计算如利用量子力学和第一性原理的方法来计算获得体系高激发态的跃迁谱线数据[10-11]，然而当体系处于高激发量子振转区域时，各种效应相互耦合干扰，导致无法获得体系正确的波函数；因此给最后的计算结果带来了不可忽略的误差，甚至有些计算结果是错误的。为了获得体系高激发量子态的跃迁谱线结构，本课题组在前期研究工作中基于微分的思想，在传统的能量表达式的基础上推导建立了差分收敛法(DCM)，对于某分子体系利用DCM方法仅需15条已知实验谱线数据和部分光谱常数便可精确计算出该体系R线系高激发态跃迁谱线[12]。本文基于包含光谱常数Lυ所在高阶项在内的R线系跃迁能谱的经典表达式，重新推导获得了仅需要11条精确的实验谱线便能准确预测出某跃迁体系R线系高激发振转态的谱线数据的另一表达形式，我们同样称该方法为DCM方法。

Na的化合物NaAs在国防工业、化学工业等方面有着广泛的用途,因而获得NaAs材料分子的内部结构及性能也越来越受到人们的关注[13-17]。1993年，Sangster等[13]通过库伦滴定法在电磁场中测量了Na-As系统的标准焓、熵、晶格指数等重要的结构参数，同时获得了这些参数的重要结果。2010年，Burtzlaff等[14]在加热的石英管中通入钠和锡的混合物，当冷却到室温时，加入适量的砷熔化，得到了Na10Sn2As6化合物以及少量的NaAs晶体。2011年，Ozisi等[15]采用第一性原理方法对NaAs分子的结构、电子态及弹性性质进行了研究。2015年，Batista等[16]使用高阶从头计算方法，得到了NaAs分子的振动能级、光谱常数、偶极矩和跃迁偶极矩。2016年，Setzer等[17]在近红外区用傅里叶变换分光计光谱技术测得了NaAs分子部分低激发振动态跃迁谱线数据。这些研究团队为人们了解NaAs材料性能做出了重要贡献；然而，由于实验和理论方法自身的局限性，以上获得的NaAs分子内部的有限信息仍然让人们无法全面掌握该材料的微观及宏观特性，这一事实的存在给该材料的进一步使用和推广形成了不小的阻碍。

本文应用新推导的解析式(7)重点研究了NaAs材料分子在电子态A30+→X10+跃迁体系(0,0)跃迁带的R线系跃迁谱线，不仅获得了实验上没能给出的该跃迁带的部分低激发振转态跃迁谱线数据，还正确预测了包含转动量子数J=80在内的高激发量子态跃迁谱线，为人们进一步掌握NaAs材料分子高激发态振转结构提供了重要信息。本文第1章对新建立的解析式(7)进行了理论推导；第2章对NaAs材料分子在电子态A30+→X10+跃迁体系(0,0)跃迁带的R线系实验谱线值和理论计算值进行了详细的分析与讨论；第3章总结了本文的工作。

1　理论与方法

双原子分子电子态R支(ΔJ=+1)跃迁谱线的经典表达形式可表示为以下形式[18]：

ν=ν0+(J+1)[Bυ′(J+2)-Bυ″J]-(J+1)2[Dυ′(J+2)2-Dυ″J2]+
(J+1)3[Hυ′(J+2)3-Hυ″J3]+(J+1)4[Lυ′(J+2)4-Lυ″J4]+…

(1)

其中：J为转动量子数；{Lυ′,Lυ″,Hυ′,Hυ″,Dυ′,Dυ″,Bυ′,Bυ″}为转动光谱常数。基于式(1)，结合微分的思想[19]，可以将跃迁谱线差v1-v2和v3-v4的差值即二次逐差表示为

(2)

式(2)可简化为以下形式：

将上式进一步变形表示为光谱常数Lυ″的函数形式

其中：

a1(J1～J4)=[(J1+1)(J1+2)-(J2+1)(J2+2)-(J3+1)(J3+2)+(J4+1)(J4+2)]；

(3-1)

a2(J1～J4)=[(J1+1)J1-(J2+1)J2-(J3+1)J3+(J4+1)J4]；

(3-2)

a3(J1～J4)=[(J1+1)2(J1+2)2-(J2+1)2(J2+2)2-(J3+1)2(J3+2)2+(J4+1)2(J4+2)2]；

(3-3)

a5(J1～J4)=[(J1+1)3(J1+2)3-(J2+1)3(J2+2)3-(J3+1)3(J3+2)3+(J4+1)3(J4+2)3]；

(3-5)

a7(J1～J4)=[(J1+1)4(J1+2)4-(J2+1)4(J2+2)4-(J3+1)4(J3+2)4+(J4+1)4(J4+2)4]；

(3-7)

对于某体系的某一跃迁带，式(3)同样适用于跃迁谱线v2～v5，可表示为

式(3)与式(4)应相等，因此可消去常数Lυ″，从而再变形得到Lυ′的函数形式

Lυ′=(ν1-ν2-ν3+ν4)b1(J1～J5)-(ν2-ν3-ν4+ν5)b2(J1～J5)-
Bυ′b3(J1～J5)+Bυ″b4(J1～J5)+Dυ′b5(J1～J5)-Dυ″b6(J1～J5)-Hυ′b7(J1～J5)+Hυ″b8(J1～J5) 。

(5)

其中：

同理，式(5)同样适用于跃迁谱线v2～v6,即有

Lυ′=(ν2-ν3-ν4+ν5)b1(J2～J6)-(ν3-ν4-ν5+ν6)b2(J2～J6)-
Bυ′b3(J2～J6)+Bυ″b4(J2～J6)+Dυ′b5(J2～J6)-
Dυ″b6(J2～J6)-Hυ′b7(J2～J6)+Hυ″b8(J2～J6)。

(6)

式(5)与式(6)应相等，进一步化简可消去常数Lυ′并得到Hυ″的表达式。以此类推，式(1)中的转动光谱常数{Lυ′,Lυ″,Hυ′,Hυ″,Dυ′,Dυ″,Bυ′,Bυ″}就可以被跃迁谱线v1～v12和相应的转动量子数J1～J12组成的表达式逐一表示，通过化简整理，最终可得到如下表达式：

ν12=ν1C1+ν2C2+ν3C3+ν4C4+ν5C5+ν6C6+ν7C7+ν8C8+ν9C9+ν10C10+ν11C11。

(7)

式中：

式(7)即为推导获得的体系R线系新跃迁谱线表达式，式中的(v1～v11)是从已知实验数据中挑选出的11条最佳跃迁谱线，v12是转动量子数J12对应的需要计算的未知跃迁谱线，C1～C11为展开系数，其中函数Ci与转动量子数(J1,J2…J12)有关。由函数Ci的定义可知，只需满足C1～C11≠0的条件下，且获得实验上精确的11条跃迁谱线数据，式(7)便能准确地预测出体系的R线系跃迁能谱。

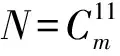
|νJ,expt-νJ,cal|→0；

(8)

|ΔJ,expt-ΔJ,cal|→0，ΔJ=νJ-1-νJ；

(9)

式中：|νJ,expt-νJ,cal|是实验值与理论计算值的差；ΔJ=νJ-1-νJ是一次谱线逐差；|ΔJ,expt-ΔJ,cal|是实验值的一次谱线逐差与理论计算值的一次谱线逐差的差值。因此，通过反复对式(7)进行计算，最终能寻找到满足物理判据式(8)至(10)的最佳(11条)跃迁谱线[vi]组合，那么所选出的这组跃迁谱线就能最好地还原该跃迁带跃迁谱线的真实物理信息。

2　应用与讨论

本文应用推导获得的新解析式(7)计算了NaAs材料分子电子态A30+→X10+跃迁体系(0,0)跃迁带的R线系跃迁谱线。表1列出了能最好地反映该跃迁带跃迁谱线真实物理信息的11条实验跃迁谱线所对应的转动量子数(J1～J11)，所选取的{Ji}不仅能很好地满足物理判据式(8)至(10)，而且还很好地保证了式(7)中的展开系数C1～C11≠0，更充分地说明了我们所选的转动量子数(J1～J11)是非常可靠的。选取的11条最佳实验跃迁谱线对应的转动量子数Jk如表1所示。

表1　选取的11条最佳实验跃迁谱线对应的转动量子数Jk

表2列出了NaAs材料分子电子态A30+→X10+跃迁体系(0,0)跃迁带R线系实验上已经测量获得的跃迁谱线子集合{vExpt}，DCM计算跃迁谱线集合{vDCM},实验谱线与DCM结果的绝对误差值(vExpt-vDCM)，逐差值(ΔJ=νJ-1-νJ)，以及相对百分误差值Error%(|vExpt-vDCM|/vExpt×100%)，表中的所有数据均以波数为单位(cm-1)。

分析表2可以发现，Setzer等[17]实验测得NaAs分子在电子态A30+→X10+跃迁体系(0,0)跃迁带R线系的35条低激发振转态跃迁谱线，而通过解析式(7)即DCM方法理论计算获得了80条高激发振转态跃迁谱线数据，不仅很好地重复了实验上得到的跃迁谱线数据，同时还精确预测了实验上没能给出的(包括转动量子数J1～J9，J15，J29，J40)多条低激发振转态跃迁谱线和高激发振转态跃迁谱线。其中实验值与DCM计算结果的最大误差(vExpt-vDCM)max=(3.560 6×10-3cm-1)(J=39)，实验值与DCM计算结果的最小误差(vExpt-vDCM)min=(-3.493 9×10-3cm-1)(J=36)，最大误差的精度在10-3量级以内。与此同时，实验逐差值ΔExpt和理论逐差值ΔDCM的差值在-0.004 2～0.004 8 cm-1。相对百分误差最大值Error%max=5.831 2×10-5(J=39)，相对百分误差最小值Error%min=1.094 1×10-6(J=13)。通过比较分析发现最大相对百分误差值在10-5量级以内，甚至小到了1/10万，该误差进一步说明利用DCM方法获得的计算结果是精确可靠的。

表2　实验上获得的跃迁谱线数据和DCM计算结果比较(单位：cm-1)

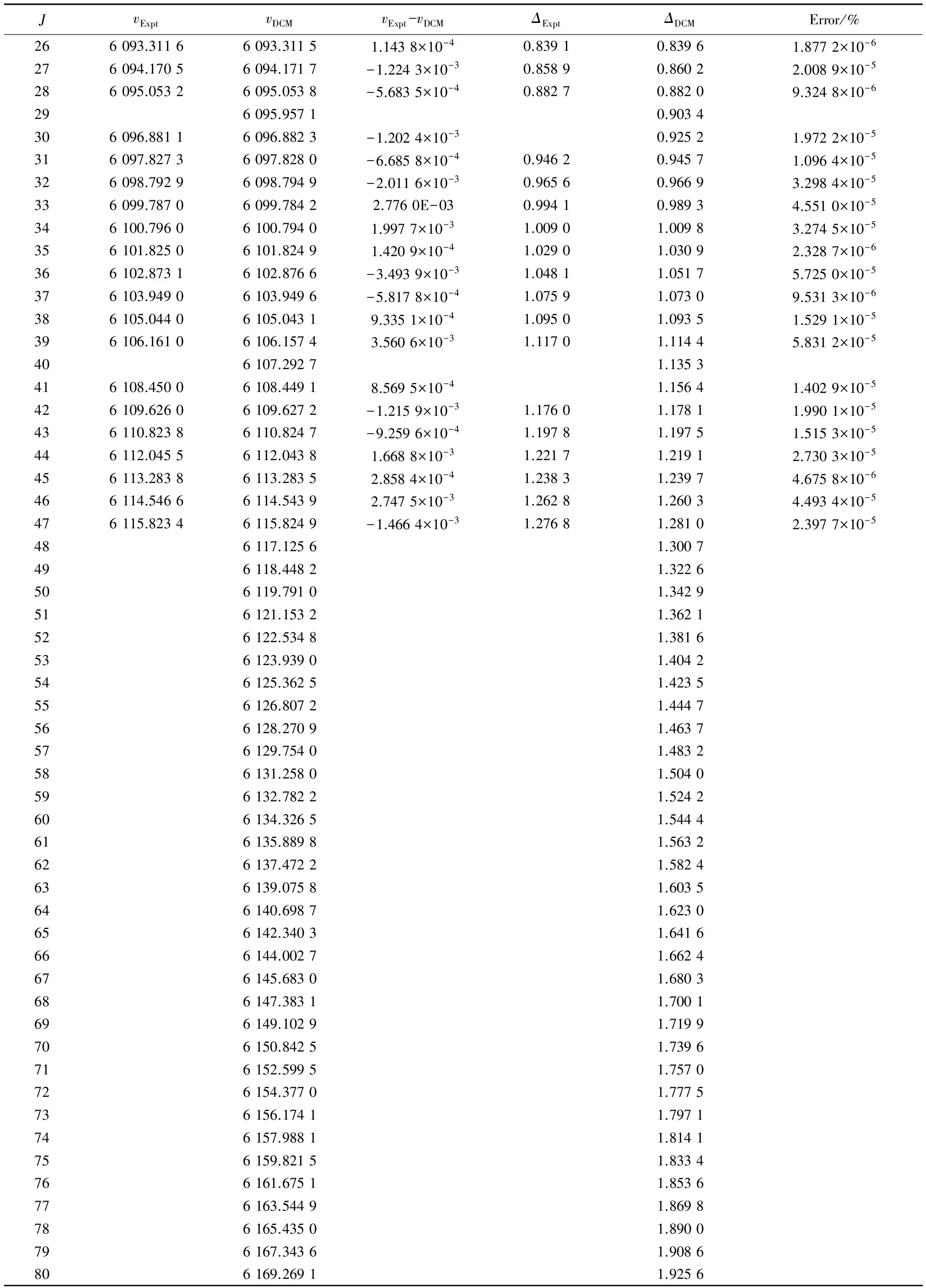
表2(续)

图1和图2分别画出了(0,0)跃迁带R线系实验值与DCM理论计算值的跃迁谱线和谱线一级逐差ΔJ=νJ-1-νJ，其中实验值用符号(“o”)表示，DCM计算值用符号(“+”)表示。从图中可以清晰直观地看出DCM计算结果不仅很好地重复了实验值，而且还发现DCM理论计算值很好地延续了实验值的发展趋势。图3清晰地画出了该跃迁带的实验值与DCM计算结果的差值(vExpt-vDCM)，其差值在-0.004～0.006 cm-1，可以看出通过理论计算获得的跃迁谱线数据几乎完全复现了实验所测得的跃迁谱线数据。

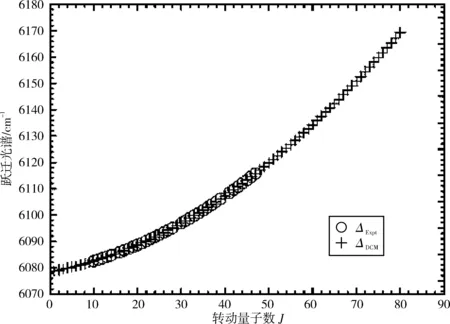
图1　NaAs分子电子态A30+→X10+跃迁体系(0-0)跃迁带R支跃迁谱线的实验值(“o”)和DCM值(“+”)的比较

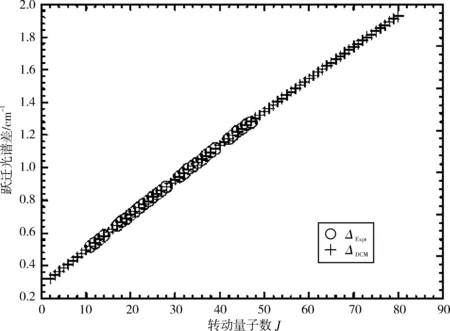
图2　NaAs分子电子态A30+→X10+跃迁体系(0-0)跃迁带R支跃迁谱线的实验值(“o”)和

图4描绘了NaAs材料分子在电子态A30+→X10+跃迁体系(0,0)跃迁带R线系的展开系数C1～C11的数值随转动量子数J的变化关系，从图中可以清晰地看出：在转动量子数J<54区域，展开系数C1～C11被限制在-20～20，在J=54附近达到极小值；当J>54时，其展开系数随着转动量子数的增大有明显的变化。其中，{C5,C11,C2,C7}的值随着转动量子数的增大而逐渐增大，{C1,C4,C10}的值随着转动量子数的增大而趋于平稳，{C6,C8,C9,C3}的值随着转动量子数的增大而逐渐减小。在这些随着转动量子数的增大而变化的展开系数Ci中，其中{C2,C3,C5,C9,C11}的变化最为明显，说明它们所对应的跃迁谱线{v2,v3,v5,v9,v11}对预测未知新谱线的误差贡献最为突出，所以在实验测量时要注意提高其实验精度。

图3　NaAs分子电子态A30+→X10+跃迁体系(0-0)跃迁带R支跃迁谱线的实验值和DCM值的相对误差(vExpt-vDCM)比较

图4　NaAs分子电子态A30+→X10+跃迁体系(0-0)跃迁带R支跃迁谱线展开系数C随转动量子数J的变化

3　总结

本文从双原子分子R线系跃迁能量的经典表达形式出发，基于课题组前期建立的差分收敛法(DCM)中的微分思想，推导获得了仅需11条已知精确的R线系跃迁谱线实验数据便可精确预测双原子分子R线系高激发振转态跃迁谱线的新解析式(7)，利用该公式研究了NaAs材料分子在电子态A30+→X10+跃迁体系(0,0)跃迁带R线系跃迁谱线。同时，通过比较分析得到了理论计算所得的低激发振转态跃迁谱线数据与实验所测得的低激发振转态跃迁谱线的数据差小于0.006 cm-1。另外，通过进一步分析发现展开系数{C2,C3,C5,C9,C11}所对应的跃迁谱线{v2,v3,v5,v9,v11}对预测未知新谱线的误差贡献最大。研究结果表明：利用新推导获得的解析式(7)式不仅计算获得了体系实验上没能给出的该跃迁带的部分低转动态跃迁谱线，还正确预测了包含转动量子数J=80在内的高激发态跃迁谱线数据，为进一步认识NaAs材料分子的微观结构与性能提供了更完善的参考数据。

[1]LI H, FOCSA C, PINCHEMEL B.Fourier transform spectroscopy of BaO:newground-state constants from the A1∑+-X1∑+chemiluminescence [J]. Journal of Chemical Physics, 2000, 113: 3026.

[2]LANG F, WINKLER K, STRAUSS C, et al.Ultracoldtriplet molecules in the rovibrational ground state [J]. Physical Review Letters, 2008, 101: 133005.1.

[3]BOLTON K, SCHLEGEL H B,HASE W L, et al. An ab initio quasi-classical direct dynamics investigation of the F+C2H2→C2H3F+H product energy distributions [J]. Phys Chem Chem Phys, 1999, 1: 999.

[4]PUZZARINI C, DE LARA-CASTELLS M P, TARRONI R, et al. Accurate ab initio prediction of the rovibrational energy leves and equilibrium geometry of carbonylselenide (OCSe) [J]. Physical Chemistry Chemical Physics, 1999, 1: 3955.

[5]WYNAR R, FREELAND R S, HAN D J,et al. Molecules in a bose-einstein condensate [J]. Science, 2000, 287: 1016.

[6]MERRITT J M, BONDYBEY V E, HEAVEN M C.Beryllium dimer caught in the act of bonding [J]. Science, 2009, 324: 1548.

[7]BERNATH P F.Extracting potentials fromspectra [J]. Science, 2009, 324: 1526.

[8]WANG R J, CHEN Y Q, CAI P P, et al.Optical heterodyne velocity modulation spectroscopy enhancedby a magnetic rotation effect [J].Chem Phys Lett, 1999, 307: 339.

[10]PACHUCKI K,KOMASA J. Nonadiabatic corrections to rovibrationallevels of H2 [J]. J Chem Phys, 2009, 130: 164113.1.

[11]GONZALEZ-FEREZR.Rovibrational spectra of diatomic molecules in strong electric fields: the adiabaticregime[J]. Phys Rev A, 2004, 69:023402.

[12]LI H D, SUN W G, FAN Q C, et al. Prediction of the rovibrational emission spectroscopy of B2∑+-X2∑+system in12C17O+[J].Journal of Molecular Spectroscopy, 2011, 83: 136.

[13]SANGSTER J,PELTONA D.The As-Na (Arsenic-Sodium) system [J]. J Phase Equilib Diff, 1993,14:240.

[14]BURTZLAFF S, HOLYNSKA M, DEHNENS.Synthesis and crystal structures of K2SnAs2and a new modification of NaAs[J].Z Anorg Allg Chem, 2010, 636: 1691.

[15]OZISIK H B, COLAKOGLU K, DELIGOZ E, et al.First principles study on the structural, electronic, and elastic properties of NaAs systems[J]. Solid State Commun, 2011, 151: 1349.

[16]BATISTA APL, OLIVEIRA-FILHOA G S, ORNELLAS F R.Ab initio characterization of the lowest-lying electronic states of the NaAs molecule[J]. Comput Theor Chem, 2015, 1064: 56.

[17]SETZER K D, FINK E H, ALEKSEYEV A B, et al. Experimental and theoretical study of the electronic states and spectra of NaAs [J]. J Mol Spectros, 2016, 320: 39.

[18]HERZEBERG G. Molecular spectra and molecular structure (I): Spectra of diatomic molecules[M]. Beijing: Science Press, 1983:15.

[19]SUN W G, FAN Q C, LI H D,et al.Studies on the P-branch spectral lines of rovibrational transitions of diatomic system [J]. Spectrochimca Acta Part A, 2011, 79: 35.