由夹芯梁弯曲谈剪切效应对许用弯矩的影响

2021-01-06吴晓

力学与实践 2020年6期

吴晓

(湖南文理学院机械工程学院，湖南常德415000)

夹芯梁由于具有质量轻、高比强度、高比刚度等优点，已在车辆工程、航空航天等实际工程中得到广泛应用。李川苏等[1]采用试验研究了结构弯曲性能。李泽华等[2]研究了泡沫铝夹层梁的三点弯曲变形行为。杨福俊等[3]研究了泡沫铝夹芯板静态三点弯曲变形行为及力学性能。方海等[4]研究了泡桐木夹层结构材料的力学性能。以上研究工作均说明了夹芯梁在实际工程中应用的重要性。孔祥清等[5]将夹芯梁弯曲实验引入到材料力学的教学实践中。文献[6-7]介绍了夹芯梁的计算方法，并把计算夹芯梁弯曲时的许用弯矩作为习题，但介绍材料力学方法计算许用弯矩时没有考虑剪切效应的影响。

1 问题的提出

材料力学教材[6]中有一道计算夹芯梁弯曲时许用弯矩的习题，矩形截面的钢、木夹芯梁，其截面形状可见图1，上、下层均为钢板，中间层为木材。

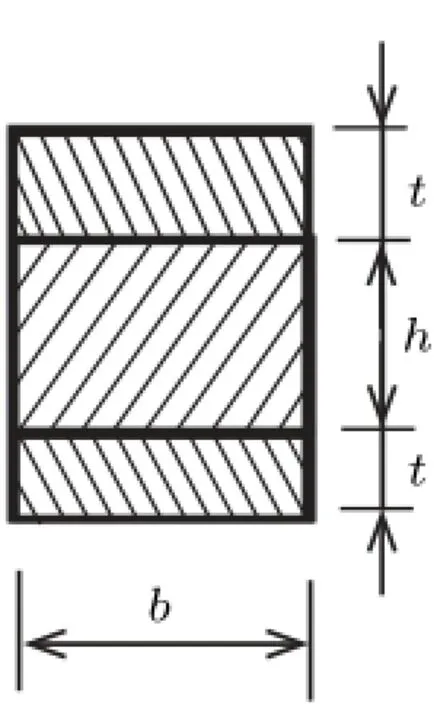
图1 夹芯梁截面

梁的计算参数为：l=3 m，b=200 mm，h=300 mm，t=12 mm，钢板的弹性模量和剪切弹性模量分别为E1=210 GPa，G1=79.38 GPa，木材的弹性模量和剪切弹性模量分别为E2=10 GPa，G2=0.5 GPa，钢、木许用应力分别为[σ1]=170 MPa，[σ2]=10 MPa。试求此梁的许用弯矩。

文献[6-7]没有介绍关于矩形截面的钢、木夹芯梁上下钢板与木芯层的连接方式，但是根据题意可以认为钢片与木材是紧密结合的。因此，本文假设矩形截面的钢板与木夹芯层间用环氧树脂粘合剂紧密粘结且梁两端用钢箍箍紧，来保证在外载荷作用下夹芯梁上下面板与夹芯层共同弯曲变形。

由文献[6-7]可知，没有考虑剪切效应时夹芯梁的弯曲正应力公式为

式中

由式(1)可知应力校核式为

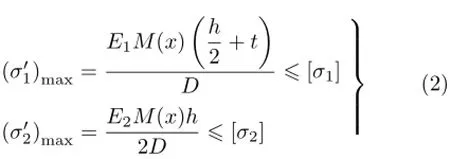
将夹芯梁参数代入式(2)中可得许用弯矩为[M]=145.13 kN·m。

梁的许用弯矩看似被求解，其实还存在问题，那就是不知道作用在夹芯梁上的是集中载荷还是分布载荷。

如果是集中载荷作用在梁上，剪切变形对夹芯梁的许用弯矩校核计算没有影响。假如是分布载荷作用在梁上，就要考虑剪切效应对许用弯矩校核计算的影响。

由材料力学可知，如果梁在各横截面上的剪力都相等，则各截面的翘曲也相同，相邻横截面间纵向纤维的长度不会因截面翘曲而改变。因此，在这种情况下横截面的翘曲并不影响纤维由弯矩所引起的纵向伸长或缩短，也就不影响根据平面假设所导出的正应力分布规律。但在分布载荷作用下，梁在各横截面上的剪力不同，各横截面的翘曲程度也不同，相邻横截面间纵向纤维的长度必然会因此而发生变化，从而影响弯曲正应力的分布。

2 剪切效应对许用弯矩的影响

本文利用材料力学方法推导夹芯梁截面的剪应力公式。

因为夹芯梁的上、下面板较薄，因此夹芯梁的弯曲可以仅考虑夹芯层的剪切刚度。

图2 所示为夹芯梁微段，左边的轴向拉力N1的表达式为同理，图2所示梁微段右边的轴向拉力N2的表达式为

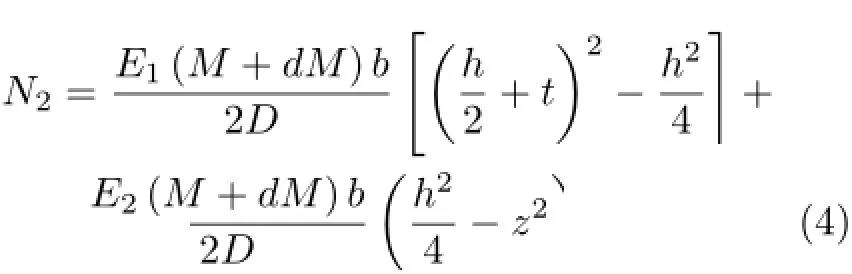
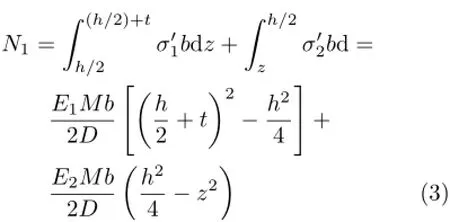
所以，图2所示静力平衡方程为

将式(3)和式(4)代入式(5)可得夹芯层横截面上的剪应力为

式中，Q=dM/dx为剪力。

图2 夹芯梁微段

由文献[8]可知，矩形截面梁在均布载荷或集中载荷作用下，其梁截面上的剪应力公式与材料力学推导出的剪应力公式是一致的，也就是说材料力学推导出的剪应力公式是二维弹性理论梁截面上的剪应力精确解，所以利用弹性体的剪应变与位移的几何方程，可以推导出考虑剪切变形时夹层梁的弯曲正应力公式。

由弹性力学可知轴向位移、横向位移与剪应力、剪应变的关系为

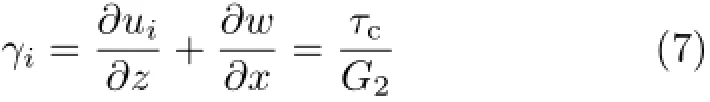
式中，ui为轴向位移，w为横向位移，γi为剪应变，i=1时代表上、下表板，i=2时代表夹芯层，G2为夹芯层的剪切弹性模量。

将式(7)对z积分一次可得

式中，Ci为待定常数。

夹芯梁中性轴处及表板与夹芯层连接处的位移条件为

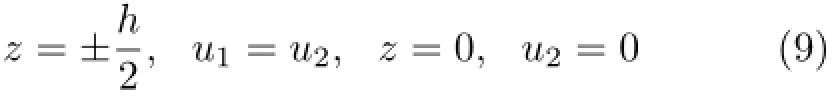
将式(6)及τ1=0代入式(8)中积分且利用式(9)可得表板及夹芯层轴向位移分别为

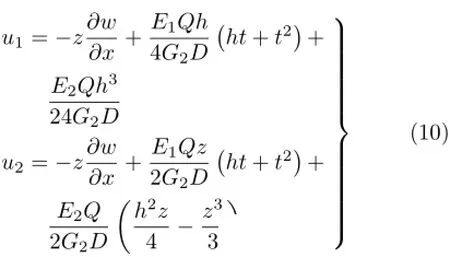
由式(10)可知夹芯梁表板、夹芯层正应力分别为

式中，q(x)=dQ/dx。

由于夹芯梁横截面弯矩方程为

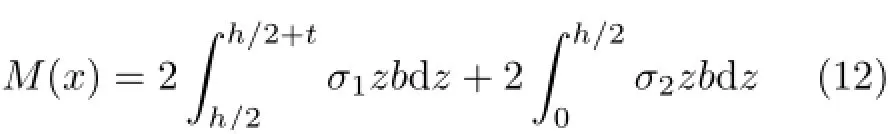
将式(11)代入式(12)中可得

式中，C为剪切刚度

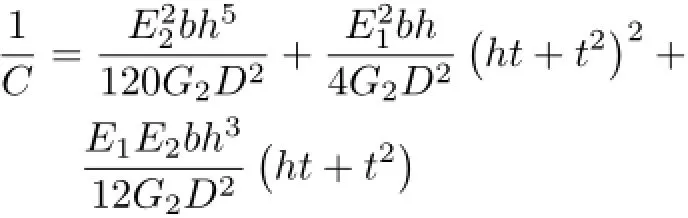
将式(13)代入式(11)中可得夹芯梁表板及夹芯层的弯曲正应力公式分别为

由式(14)和式(15)可以看出夹芯梁在分布载荷作用下，分布载荷对梁的弯曲正应力有一定影响。当夹芯梁在集中力作用下，式(14)和式(15)即退化为式(1)。

为了检验本文式(14)和式(15)的计算精度，以简支梁为例，可令q(x)=q，E=E1=0，t=0，所以式(15)可化为

式中，I=bh3/12，A=bh，G为剪切弹性模量。

利用E=2G(1+μ)，可把式(16)化为

式中，μ为泊松比。

在式(17)中令μ=0可得

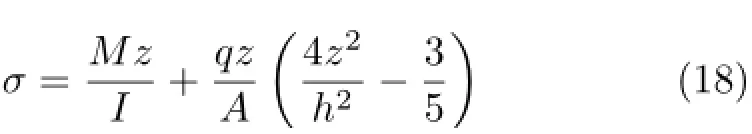
即文献[8]给出的均布载荷作用下简支梁截面正应力的弹性理论精确解。

参阅文献[9]可令μ=0.25时，由式(17)和式(18)可得图3所示简支梁截面最大弯曲正应力分别为

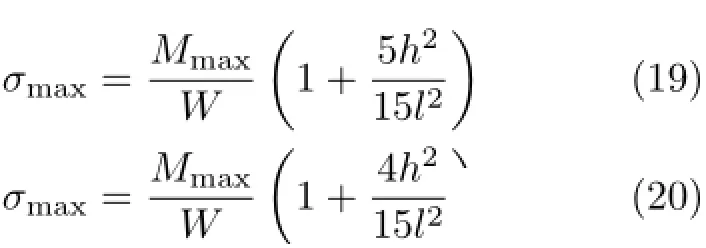
式中，W=bh2/6，Mmax=ql2/8。

图3 均布载荷作用下简支梁

式(19)和式(20)计算的结果列在表1中，以便比较计算精度。

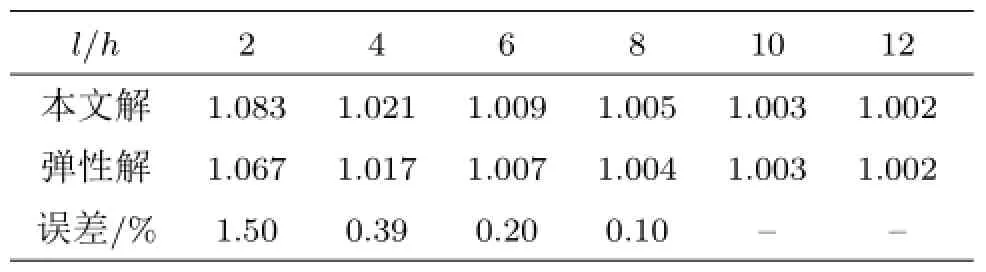
表1 最大弯曲正应力系数β

表1 中，σmax=β×Mmax/W，由表1可以看出本文方法计算精度非常高。

下面以图3所示均布载荷作用下简支夹芯梁为例，采用式(14)和式(15)分析剪切效应对许用弯矩的影响。

将有关计算参数代入式(14)可得夹芯梁的最大正应力为

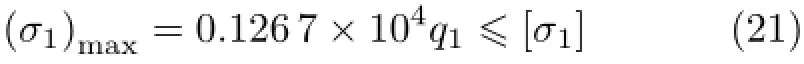
由式(21)可以求得

将有关计算参数代入式(15)可得夹芯梁的夹芯层最大正应力为

由式(23)可以求得

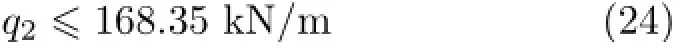
比较式(22)和式(24)可知作用在图3所示夹芯梁的许用均布载荷应该为q1=134.175 2 kN/m。所以，考虑剪切效应时图3所示夹芯梁上的许用弯矩为

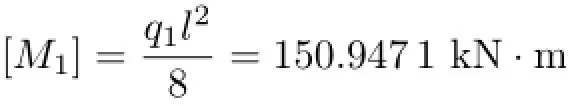
所以，文献[6]方法计算的许用弯矩与本文方法计算的许用弯矩的误差为

以上计算说明剪切效应对均布载荷作用下夹芯梁的许用弯矩还是有一定影响的，虽然实际工程中一般要求计算误差不超过5%，而本文方法的计算误差也仅为4.01%。但是，对于设计精度要求高的结构来说4.01%也是较大的误差。众所周知，梁的跨高比越小剪切效应对梁的弯曲变形计算影响就越大，尤其是对夹芯梁的弯曲变形，以l/(h+2t)=9.26的简支夹芯梁为例来计算夹芯梁的许用弯矩，如果夹芯梁的跨高比l/(h+2t)更小，文献[6]方法计算的许用弯矩与本文方法计算的许用弯矩的误差会更大。

在材料力学的实际教学中，如果让学生掌握本文关于夹芯梁许用弯矩的计算方法是有一定困难的，但是作为材料力学教师是应该掌握的。在关于夹芯梁内容的教学过程中，教师应该告诉学生剪切效应会对夹芯梁的弯曲变形计算产生较大影响。