虚物质导数与局部变分
——张量变分学的基本概念及其定义1)
2021-01-06殷雅俊
殷雅俊
(清华大学航天航空学院工程力学系,北京100084)
本文标题涉及了三个关键词:虚物质导数、局部变分、张量变分学,其中,虚物质导数和局部变分是似曾相识的词汇:虚物质导数似乎只是在经典物质导数前面加了一个“虚”字;局部变分似乎只是在经典变分前面加了一个限定词“局部”。
读者也许会有疑问:“为何多此一举?”“这不是玩弄词藻吗?”作者的辩解如下。引入虚物质导数和局部变分概念,是为了实现三个意图:一是弥补张量分析学概念体系中破缺的对称性;二是为张量变分学奠定基础,三是为张量的协变变分学开辟道路。
限于篇幅,本文主要聚焦于前两个意图,即概念体系的对称性和张量变分学。而张量协变变分学,则是后续文章综述的重点。本文包括如下内容:(1)简要回顾经典变分思想,评述其概念上的局限性;(2)拓展经典物质导数,引入虚物质导数概念;(3)依托虚物质导数,类比张量微分概念,定义张量局部变分概念,塑造张量变分与张量微分之间的对称性;(4)类比张量微分学,展示张量变分学,揭示张量变分学与张量微分学之间的对称性。
1 变分:一个“一句话说不清楚”的概念
大学时代,学习数学分析。课堂上,老师提出要求:“微分与积分的关系是什么?请用一句话说清楚。”作者小心翼翼地回答:“逆运算。”老师挑起大拇指:“高,实在是高!用一句话说清楚已经相当不易,你竟然用一个词就说清楚了。”高兴之余,老师进一步提高标准:“请用一个字说清楚!”受到老师的称赞,信心大增,脱口回答:“逆!”
当年老师的苛刻要求,产生了持久的影响。从此,作者养成了思维习惯:对重要的概念,一定要理解到这样的程度--用一句话说清楚其内涵和外延。
后来,学习力学中的变分原理。作者突然发现,如果问:“什么是微分?”一句话能说清楚。如果问:“什么是变分?”一句话竟然说不清楚了。
2008年,作者曾被前辈追问:“怎样理解变分?”作者谨慎地“用一句话”答道:“对参变量的导数。”虽然用了“一句话”,但似乎并没有“说清楚”。实际上,这个说法,对数学学者尚可接受,但对力学学者仍显费解。
如果继续追问:“什么东西对参变量的导数?”作者能给出的答案是“泛函对参变量的导数”。这个答案当然不算错,但有局限性。
2 从历史的天空看经典变分概念的整体性
历史地看,变分似乎是个整体性概念。
整体和局部及其相互关系,是哲学家关注的问题,也是自然科学家感兴趣的问题。
早年学习弹性力学,作者深受如下陈述的影响:弹性力学的基本问题有两种提法,一是微分提法,二是变分提法。后来,作者自己成了教师和学者,对两种提法有了更深刻的理解:微分提法体现了牛顿和莱布尼兹的局部化数理分析思想,而变分提法则体现了欧拉和拉格朗日的整体化数理分析思想。
由此,作者树立起了牢固的观念:微分是局部性概念,变分是整体性概念;
微分被定义在一个点的邻域内,变分被定义在物质构型空间上;微分提法对应局部化数理分析之路,变分提法对应整体化数理分析之路。
从力学的角度看,上述观念似乎经得起时间考验。场函数的微分,涉及空间域上“点的邻域”内场函数的增量。“点的邻域”当然是局部性概念。弹性力学中的运动微分方程,建立在微单元体上。微单元体是“点的邻域”的几何化形态,自然是局部性概念。
泛函的变分,是定义在物质构型空间上的泛函的增量。弹性力学有最小势能原理和最小余能原理。两个原理分别涉及势能泛函的变分和余能泛函的变分。势能泛函和余能泛函都表现为物质构型空间上的积分。物质构型空间是整体性的概念,泛函自然也是整体性概念。
分析力学有最小作用量原理。克莱恩在他的名著《古今数学思想》中指出:“变分学的早期工作几乎不能和微积分区分开来。但是,随着变分法的深化,牛顿之后的伟大先驱们很快意识到:一个全新的、具有自己的特征问题和方法论的数学分支已经产生了。”“这个新学科,对于数学和科学来说,其重要性几乎可以和微分方程相比,它为整个数学物理提供了一个最重要的原理。”这个“最重要的原理”,即最小作用量原理。
作用量一般表现为时间段上的积分。当说“作用量的变分”时,研究的是定义在时间段上的作用量的增量。时间段是整体性的概念,作用量当然也是整体性的概念。
很显然,先驱们思考变分学的角度,着眼于整体。其中的核心概念,是泛函的变分或作用量的变分。
然而,这产生了误导,使得作者产生了如下误解:由于变分的作用对象都是整体性概念,故变分就是个整体性概念。教学过程中,作者有意无意地将这样的观念传递给了学生。
近年来,随着研究的深入,作者意识到,上述观念限定了教师和学生的想象力。实际上,如果研究对象不是泛函或作用量,而是张量场函数,那么,着眼点就不应该是整体,而应该是局部。
3 张量变分的局部性与概念体系对称性的破缺
2002年,作者研究生物膜力学时,强烈地意识到,需要清晰地引入一个概念--曲率张量的变分。
生物膜是软物质,可以将其抽象成柔性曲面。不难想象,柔性曲面几何形状的任何涨落,都会诱导曲率张量的扰动。那么,怎样才能最有效地度量曲率张量的扰动量?
当时,作者借鉴弹性力学,用虚位移概念刻画柔性曲面的涨落。于是,很自然地,就把曲率张量的扰动量视为“曲率张量的变分”。
如何快速计算曲率张量的变分?作者意识到,不同于曲率张量的微分,“曲率张量的变分”没有现成的计算模式,故当时只能凭物理直觉“拼凑”出其计算式。
数学力学中的概念,一般都有两个表达式,一个是定义式,另一个是计算式。其中,定义式在先,计算式在后,计算式源自定义式。“曲率张量的变分”作为一个基本概念,既没有计算式,也没有定义式。因为没有定义式,当然也就无法“一句话说清楚”其内涵和外延。
“曲率张量的变分”,无定义,难计算。然而,“曲率张量的微分”,可定义,可计算。作者发现,类似的概念上的对称性破缺,不是孤立的现象,竟然普遍存在于张量分析中:有一般意义上的“张量微分”概念,但没有一般意义上的“张量变分”概念。
作者还发现,概念上的对称性破缺带来的直接后果,是理论上的对称性破缺:张量微分学的大厦巍然挺立,但张量变分学的原野却一片荒漠。这并不奇怪:基本概念是理论的基石。张量微分学的大厦奠定在张量微分概念的基础之上。相反地,缺少了基础性的张量变分概念,张量变分学的大厦就无从谈起。
追根溯源,可以发现,对称性破缺的根本原因,源自局部性概念与整体性概念之间的错配:张量场函数可以是局部性概念,微分是局部性概念。这样,“张量场函数/微分”就是两个局部性概念的组合,浑然天成。然而,经典的变分“被认为”是整体性概念,“张量场函数/变分”,是局部性概念与整体性概念的叠加,难以匹配。
作者想起智者的忠告:纷繁之处,可尝试分类;混淆之处,可尝试定义。显然,要纠正概念组合的错配,最便捷的方法是塑造出一个局部性概念--张量场函数的“局部变分”。这样,就相当于对笼统的变分概念进行了更精细的分类--整体性变分和局部性变分。当然,局部变分概念难以借助经验提炼出来,只能借助理性塑造出来。
4 张量场函数的虚物质导数——局部变分概念的逻辑基础
如何塑造张量场函数的局部变分概念?作者的作法是“先为局部变分概念寻找一个逻辑基础”。2016年,找到了突破口:作者从“虚”字上获得了灵感。
力学史上,从“实”到“虚”的观念进化,对应着重要的思想飞跃。分析力学和弹性力学,都涉及一个十分基本的概念--虚位移。弹性力学中虚位移的定义很简洁:就是运动许可位移。满足运动许可的虚位移有无穷多,构成无穷集合。而真实位移只是虚位移的特例,只是无穷集合中的特殊元素。
分析力学中,“虚”字照样引人注目。分析力学的理论体系,可以被奠定在不同的基本原理基础之上:拉格朗日方程,被奠定在达朗贝尔原理的基础之上;吉布斯阿佩尔方程和凯恩方程,被奠定在高斯原理的基础之上。从达朗贝尔原理到拉格朗日方程,虚位移概念发挥了重要作用。同样,从高斯原理到吉布斯阿佩尔方程和凯恩方程,虚加速度概念不可或缺。
在速度和加速度之间,还有一个运动学量--虚速度。虚速度,就是运动许可速度。历史上,虚速度概念并没有逃过先驱们锐利的眼睛。分析力学中,除了达朗贝尔原理和高斯原理,还有约旦原理。虚速度是约旦原理中决定性的概念。
注意到,位移,速度,加速度,不论“虚实”,都是定义在物质点上的概念。论及“物质点”,连续介质力学的一个概念进入了作者的视线--物质导数。
需要说明的是,几何论中,确有“对参变量的导数”概念。如果“参变量”被取为时间变量,且“对参变量的导数”被定义在运动的物质点上,即可得到物质导数[1-2]。
在作者的印象里,物质导数是“实”的概念,用以刻画物体“真实”的运动。后来,作者意识到,这只是先入为主的自我设限。实际上,没有任何理由认为,也没有任何权力规定,物质导数必须是“实”的。正如虚位移、虚速度和虚加速度,完全可以自由地引入“虚”物质导数概念。正如虚位移是运动许可位移,虚物质导数即为运动许可物质导数。
虚物质导数,可以视为实物质导数的推广。反过来,实物质导数,可以视为虚物质导数的特例。
从虚物质导数概念出发,就可以定义局部变分概念。也就是说,虚物质导数,可以被选定为局部变分概念的逻辑基础。
一旦涉及到物质导数,就得关注物质占据的空间及其运动的描述方式。
5 物质空间及其运动描述方式
为了简化形式,采用平坦空间。至于运动的描述方式,最基本的有欧拉描述和拉格朗日描述[1]。本文采用拉格朗日描述,是为了简化理论的解析结构。简化到极致,读者便可轻松地理解本质和思想。
平坦空间拉格朗日描述下,张量场函数T具有如下函数形态

T既是拉格朗日坐标xm的函数,也是时间参变量t的显态函数。这里的时间t,是一般参变量的特殊情形。从数学的角度看,xm和t都是自变量,地位完全平等,没有本质的差异。然而,如果从力学的角度看,xm被赋予了几何意义和物理意义,t则被赋予了物理意义。此时,xm是自变量,t是参数。物理学和力学中,被xm刻画的连续函数,大都是“场”函数。
嵌入在连续体上的拉格朗日坐标xm的集合构成了一个实数域,称之为拉格朗日空间域。连续体的运动发生在某个时间段内。这个时间段也构成一个实数域,称之为拉格朗日时间域。张量场函数T(xm,t)在空间域上的变化,引出经典微分,在时间域上的变化,引出局部变分。
拉格朗日描述下,时间t与坐标xm居于同等地位。时间域与空间域也居于同等地位。时间t的引入,可以从运动的角度看变分概念的本质。
注意到,作用量中包含了时间,故似乎是动态概念。而连续介质力学中的势能泛函和余能泛函,似乎都是静态的概念。也就是说,能量泛函中没有引入时间。当然,“没有引入时间”,不等于“没有时间概念”。能量泛函的增量(或变化)是物体运动的结果,而运动总发生在某个时间段内。因此,能量泛函中本来就有时间。实际上,理解了本文之后,读者就会意识到:一旦允许时间自变量出现在能量泛函中,能量原理就会容易理解得多。
为便于读者理解,下面采用比较分析法,同时展示张量场函数在空间域上的经典微分和时间域上的局部变分。
6 张量场函数在空间域上的经典微分
研究拉格朗日空间域中的微分,只需保持拉格朗日时间参变量t不变。固定时间参变量t,相当于令时间“凝固”或“冻结”。此时,看到的是t时刻静态的物质空间。令拉格朗日坐标xm产生一个增量Δxm,进而求张量场函数T的增量ΔT

由于拉格朗日坐标xm对应于物质点,因此,式(2)的含义是物质点(xm+Δxm)的张量值与物质点xm的张量值之差。
大战在即,豆腐坊的生意却比往日更繁忙。假如不是四周枪炮林立,不是当街口一堆堆叠得小山似的沙包,还有沙包后伸出来的轻重机枪,光看豆腐坊的生意还真和平日里没啥两样:几大口铁锅一溜排开,火头正旺,入了锅的豆腐水滋滋冒着泡;几个伙计光着膀子,系着围裙,正抬着一大桶豆腐水往木格子里倒,只消一会,点了卤的豆腐就结得硬硬邦邦。
固定时刻t,在xm的邻域内,将T(xm+Δxm,t)展开为泰勒级数

这里的泰勒级数,是场函数T(xm+Δxm,t)在拉格朗日空间域上的展开形式。于是式(2)重写为

由式(4)右端的一阶项,就可以定义出拉格朗日空间域上张量的微分dT

式(5)可以推广到任意场函数。
经典偏导数∂T/∂xm和经典微分dT,是张量微分学的基础性概念。这两个概念定义之后,张量微分学的理论体系,就大体上确定了。
7 张量场函数在时间域上的局部变分
研究拉格朗日时间域中的变分,只需保持拉格朗日坐标xm不变,令拉格朗日时间t产生一个增量Δt,进而求张量场函数的增量ΔT

在t的邻域内,将场函数T(xm,t+Δt)展开为泰勒级数
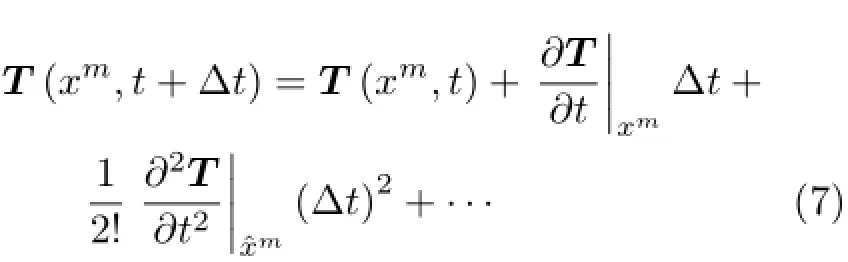
这里的泰勒级数,是场函数T(xm,t+Δt)在拉格朗日时间域上的展开形式。展开过程中,保持拉格朗日坐标xm不变,亦即紧盯运动的物质点不变。根据拉格朗日描述下物质导数的定义,式(7)可重写为
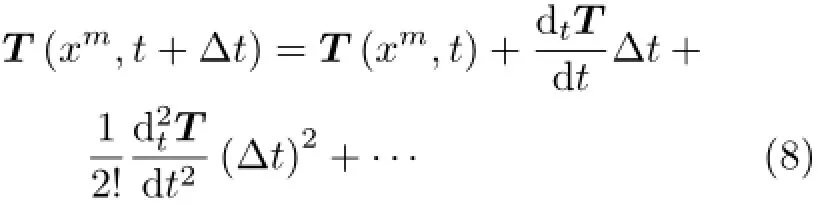
式(8)代入式(6),可写出

由式(9)右端的一阶项,可以定义出拉格朗日时间域上张量场函数的微分dtT

确切地说,dtT是张量场函数T对时间t的微分。由于dtT是定义在物质点xm上的随体概念,因此是“物质微分”。式(10)显示,物质微分dtT是与物质导数dtT/dt对应的概念,二者之间成正比例关系,比例系数为dt。
如果dtT/dt是虚物质导数,则dtT就是虚物质微分。此时就将dtT称为“张量场函数T的局部变分”。
式(10)中的定义可推广到任意场函数。也就是说,任意场函数的局部变分,都可以通过其虚物质导数来定义。
虚物质导数dtT/dt和局部变分dtT,是张量变分学的基础性概念。这两个概念定义之后,张量变分学的理论体系,就大体上确定了。
8 张量场函数的经典微分与局部变分之间的对称性
式(5)包含了两个基本概念:拉格朗日空间域上,张量场函数T的偏导数∂T/∂xm和微分dT。式(10)也包含了两个基本概念:拉格朗日时间域上,张量场函数T的虚物质导数dtT/dt和局部变分dtT。
空间域xm与时间域t是对应的。空间域与时间域上成对儿的基本概念,存在“一一对应”的对称性
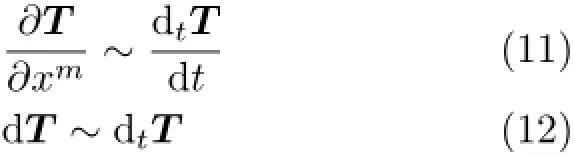
上述对称性,既包含表观形式的对称,也包含解析结构的对称。画出如下对称示意图

注意到概念“名称”的对称性:dT是微分,dtT是变分。继续类比,∂T/∂xm是微商,即微分之商;dtT/dt是变商,即变分之商。
至此,“张量的经典微分~张量的局部变分”之间的对称性,就被建立起来了。这两个概念极具基础性。基于这两个基础性的概念,可以发展出来更多的概念、思想和理论。于是,一个有趣的问题值得追问:两个基础性概念之间对称性“基因”,能否稳定地被“遗传”下去?或者说,后继的概念、思想和理论,能否葆有对称性?答案是肯定的。
如上所述,基于偏导数∂T/∂xm和微分dT,可以发展张量场函数的微分学;基于虚物质导数dtT/dt和局部变分dtT,可以发展张量场函数的变分学。可以预料,张量变分学与张量微分学,也是对称的,即

可以肯定,对于张量微分学中的表达式,张量变分学中都存在与之对称的表达式。
9 拉格朗日基矢量的经典微分和局部变分之间的对称性
任何成熟的理论都必须具有可计算性。从哪个角度审视张量变分学的可计算性?为便于参照,仍然从对称的角度看问题。回顾一下张量微分学,可知有如下命题:基矢量微分的可计算性,是张量微分学可计算性的基础。拉格朗日协变基矢量gi和逆变基矢量gi的函数形态为

张量微分学中,有著名的克里斯托弗尔公式[1-2]
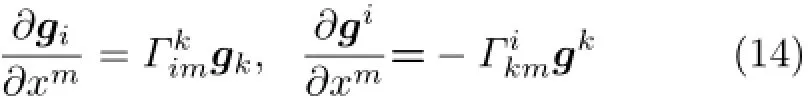
空间域上,克里斯托弗尔公式刻画了拉格朗日基矢量的空间变化率。基矢量的空间导数,仍然是基矢量的组合,组合系数是Γkim。克里斯托弗尔公式是张量微分学的重要基础之一。Γkim被称为克里斯托弗尔符号。克里斯托弗尔符号的定义,是克里斯托弗尔对张量微分学的伟大贡献。
基于式(14),可导出基矢量的经典微分
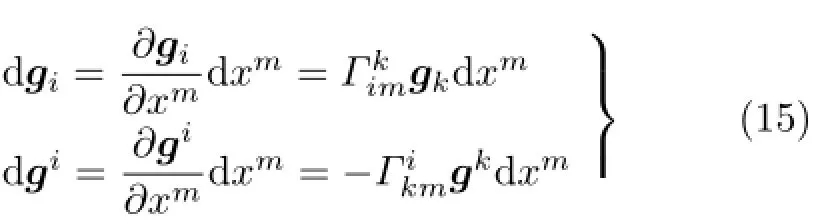
基矢量的空间微分dgi,仍然是基矢量gk的组合,组合系数是
可以从历史中获得借鉴:基矢量局部变分的可计算性,是张量变分学可计算性的基础。时间域上,拉格朗日基矢量的物质导数为[1]
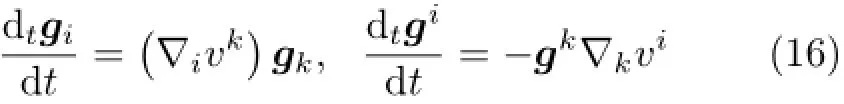
式中,vi是速度场矢量v=vigi的拉格朗日逆变分量。式(16)是张量分析学中的经典结果。基矢量的物质导数,仍然是基矢量的组合,组合系数是速度分量vk的协变导数(或速度梯度∇v的分量)∇ivk。
如果速度场v是“虚”的,则式(16)给出了基矢量的虚物质导数。显然,拉格朗日基矢量的虚物质导数,取决于虚速度场的梯度∇v。
式(16)与式(14)显示出对称性。与式(14)在张量微分学中的基础性地位类似,式(16)是张量变分学的重要基础。基于式(16),可导出基矢量的局部变分
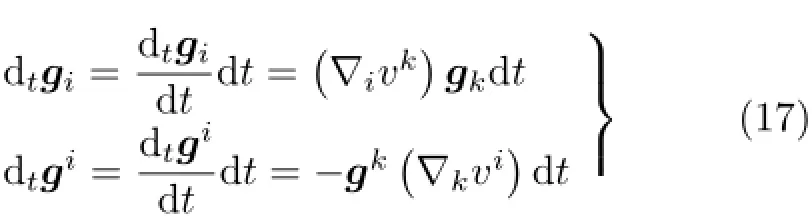
基矢量的局部变分dtgi,仍然是基矢量gk的组合,组合系数是(∇ivk)dt。
一旦确定了虚速度梯度分量∇ivk,则张量变分学中的任何计算,都可顺利地给出确定的“值”。
从式(16)和式(17)中可获得启示:如果看到的是实速度场,那么,式(16)就给出了基矢量的实物质导数,式(17)就给出了基矢量的“实”时间微分。如果看到的是虚速度场,那么,式(16)就给出了基矢量的虚物质导数,式(17)就给出了基矢量的“虚”时间微分(或虚物质微分),亦即局部变分。总之,只要速度场有虚实之分,基矢量的物质导数就有虚实之分,基矢量的时间微分就有虚实之分。而虚的时间微分,就是局部变分。
式(17)与式(15)之间的对称性,清晰可见。
限于论文的篇幅,这里不再继续展示张量变分学与张量微分学的对称性。如果读者有兴趣,可以自己尝试一下:比照张量微分学的大厦,一定可以构筑出张量变分学的大厦,且两座大厦遥相呼应,构成优雅对称的建筑群。
10 张量概念中的协变性思想及其推广
对称性的遗传进程连绵不断,当然也可以持续追问:对称的张量微分学和张量变分学之后,是否还能塑造出更宏大的对称建筑群?
答案是肯定的。但要塑造出新的对称建筑群,必须先引入一块厚重的基石--协变性思想。理由如下。
标题中,出现了张量一词。实际上,即使没有张量这个词,本文照样言之成理。之所以画蛇添足地加上这个词,是为后续建筑群的对称化做铺垫。
数学力学的历史上,张量概念的诞生是件大事。不同于经典力学概念,张量概念中蕴涵了一个既漂亮又深刻的思想--协变性思想。
1935年,法国诞生了著名的布尔巴基学派。该学派提出了重要的思想观念--数学结构。在诸种类型的数学结构中,最基本的是代数结构。张量就是普遍存在于物理学和力学中的代数结构。
作为代数结构,张量有内部子结构,例如,分量和基矢量。子结构满足特定的协调约束性质,即“协变性”,具体表现为两大基本变换:一是指标升降变换,二是坐标变换。作者将二者合称为里奇变换[3-4]。
确切地说,协变性就是张量在里奇变换下的不变性。正是协变性,保证了张量的坐标无关性。从这个意义上讲,在物理学和力学中,协变性近乎于客观性。因此说,协变性思想,不仅漂亮,而且深刻。
从张量代数学到张量微分学的演进,是数学物理和数学力学史上的大事。但这件大事总被一种不大圆满的氛围所笼罩--张量微分的协变性退化了。丧失了协变性的张量微分,对物理学和力学不吝一场灾难。
危难时刻,意大利的里奇学派尽显英雄本色:他们巧妙地引入了漂亮的新概念--张量的协变微分,从而一举将不协变的微分学,“美化”成了协变的微分学。
然而,随着协变微分概念的诞生,概念上新的对称性破缺出现了。随着协变微分学的出世,理论上新的对称性破缺出现了。
本文刻画了这样的历史轨迹:先驱们定义了张量微分,造成了概念上的对称性破缺。而随着张量变分的定义,概念上的对称性破缺得以弥补。先驱们发展了张量微分学,造成了理论上的对称性破缺。而随着张量变分学的建立,理论上的对称性破缺得以修复。
现在,新的对称性破缺引出了新的问题:还能重复上述对称化历史的轨迹吗?答案是肯定的。对称的建筑群将被持续延拓,规模更大、更为壮丽的对称建筑群将拔地而起。如果读者想一睹其真容,那就请阅读后续文章吧。
11 说不尽的对称
结束本文时,再关注一下对称性。对称是自然科学永恒的主题。历史上,很多伟大学者都涉及过这个主题,例如,赫尔曼·外尔的《对称》。当然,作者最喜欢前辈力学家武际可先生的对称性思想。他的文集《动脑筋·说力学》[5-6]中,有两篇文章涉及对称,一是“谈谈对称”,二是“从太极图说起--再谈对称”。两篇文章深入浅出,娓娓道来对称思想之精髓,令人大开眼界,受益无穷。
读者一定会问:“为什么对称观念如此令人着迷?”德国数学家诺特有著名的命题:任何对称性,都对应着某种形式的守恒律。物理学和力学的历史已经确证了命题的正确性:物理学和力学的每一条规律,都受到某种对称性的支配;任何新对称性的发现,都意味着新规律的诞生;任何对称性破缺的出现,都意味着新理论的曙光。诺特的命题极大地消减了探索的盲目性--只要捕捉到对称性,就可以顺藤摸瓜地找到守恒律。本来,追寻守恒律,是物理学和力学探索者永恒的使命。诺特命题之后,追寻对称性,成为物理学和力学探索者达成使命的捷径。
这也正是作者在本文中的动机之所在:苦心孤诣地塑造经典微分与局部变分之间的对称性。
12 结论
结束本文时,作者抛出一个疑问:虚物质导数是不可或缺的概念吗?实际上,早在2016年,作者就直接从实物质导数出发,引出了局部变分概念。当时,没有感到有何不妥之处。从前几年的探索看,似乎有实物质导数概念就足够了。这样看来,虚物质导数概念似乎有些多余。引入虚物质导数,似乎违反了“奥卡姆剃刀”原则:如非必须,勿加实体。
后来,作者否定了“多余”的判断。作者并不是想通了,而是类比之余,坚定了信念:已经有实位移,但从没有认为,虚位移概念是多余的。已经有实速度,但从没有认为,虚速度概念是多余的。已经有实加速度,但从没有认为,虚加速度概念是多余的。
换个角度看:如果说,张量的局部变分是个不可或缺的概念,那么虚物质导数,就是个必不可少的概念。虚物质导数和局部变分概念的威力,会在后续的文章中,充分地展现出来。
本文只涉及了拉格朗日描述。欧拉描述,照样可以揭示出对称的张量微分学和张量变分学。换言之,张量微分学与张量变分学之间的对称性,是一种客观实在,与运动的描述方式无关。不论采用何种运动描述方式,对称性都存在。但限于篇幅,本文不再涉及欧拉描述。
在传统观念中,张量分析学主要是指张量微分学。现在,可以更新观念:张量分析学包括了两个对称的理论体系:一个是张量微分学,另一个是张量变分学。
本文讲述了一个对称性故事,后续文章将讲述对称性故事的续集。
