扭杆式履带车辆机电悬架的非线性随机最优振动控制1)

严京玺 夏 磊 宋慧新 宦荣华，2) 朱位秋(浙江大学航空航天学院，杭州310027)

†(中国北方车辆研究所，北京100072)

现代战争对履带车辆行驶的平稳性提出了更高的要求，运行平稳性对于改善作战人员作战环境与提高履带车辆行进间火炮射击精度有着极其重要的意义[1]。而要让履带车辆适应复杂多样的战争地形，先进的悬架系统至关重要。履带车辆悬架系统连接车体与负重轮，一般包含弹性支撑元件和减振装置等，具有缓冲地面冲击、减少车体振动的作用，一般可分为被动、主动与半主动三种类型。当前国内履带车辆多采用被动悬架，然而由于被动悬架刚度与阻尼无法调节，已经无法满足现代战争的高要求。半主动悬架由于结构简单、能耗较低、相对可靠等优点，具有较好的应用前景，其中最典型的就是利用磁流变阻尼器的半主动悬架。然而磁流变阻尼器具有易沉淀等缺陷，离实际应用还有一段距离。主动悬架能够根据车体实时状态提供主动力，故而在合适的控制策略下，可以起到很好的控制效果。当前，世界各国都致力于主动控制履带车辆悬架的研究，英、美等发达国家已经率先研制出了一些型号的主动悬架履带车辆，而我国在这方面的研究还不够成熟。有效的控制策略是半主动和主动悬架的核心技术，不合适的控制算法不仅不能减小车体振动，还可能会引起车体更大振动甚至失稳。国内外学者对车辆悬架的控制方法进行了大量的研究[2-7]。现有的控制策略主要分为三类[8]，第一类适用于简单的控制系统，以“天棚”控制[9]为代表，这种控制方法设计简单但控制效果不够理想。第二类适用于线性时不变系统，主要有线性最优控制[10]、最优预见控制[11]等。第三类适用于强非线性系统，主要有模糊控制[12]、神经网络方法等，这些算法都不是基于精确数学模型，虽然具有较好的鲁棒性，但是控制效果有限。扭杆式空气弹簧悬架由于空气弹簧和扭杆的斜置设计，在复杂路面上运行时表现出非常强的非线性特征，这类悬架的随机振动控制一直以来都是一个难点问题。近20多年来，浙江大学朱位秋团队对多自由度强非线性随机振动系统的最优控制进行了系统而深入的研究[13-15]，为本文的研究提供了理论基础。

本文基于随机最优控制理论方法，研究了扭杆式履带车辆机电悬架的非线性随机最优控制。首先基于空气弹簧的非线性模型[16-18]，建立了扭杆式机电悬架的非线性随机动力学模型。随后，根据随机动态规划原理建立并求解机电悬架系统相应的动态规划方程，考虑到电机执行器的执行能力有限，确定了随机最优有界控制律。最后，通过仿真分析对提出控制规律的控制效果进行了评估，并且讨论了控制力时滞对控制效果的影响规律。

1 悬架系统建模

扭杆式履带车辆一般由车体和多个负重轮组成，单个负重轮和车体之间通过扭杆、空气弹簧和电机作动器连接组成悬架系统。由于实际运行过程中，每个悬架系统是通过电机作动器独立控制的，因此，本文主要研究单个悬架的随机最优控制问题，其简化模型如图1所示。

图1 履带车辆机电悬架系统模型简图

悬架系统具有两个自由度，分别为车体的垂向运动与扭杆的转动，分别用yc与转角α表示。车轮通过履带与地面接触，车轮与地面的接触一般表示为接触刚度为kw的弹簧，其原长设为r0。x轴表示路面基准线，路面激励用随机过程yr(x)表示，通常可以用路面不平顺谱来描述其统计特性。图1中δ为OC与水平的夹角，θ为OC与BC的夹角，γ为OC与OB的夹角。

负重轮通过空气弹簧与车体连接并对车体进行支撑，空气弹簧简化模型如图2所示。空气弹簧结构和动力学参数如表1所示。

表1 空气弹簧参数

图2 空气弹簧模型

根据空气弹簧的结构，建立其力学模型为

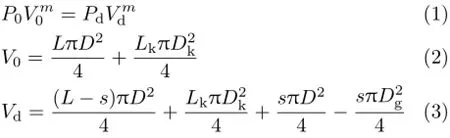
式中，V0与P0分别为空气弹簧初始体积与初始压强，Vd与Pd分别为活塞运动s时的空气体积与压强，F为活塞杆受力。由几何条件可得

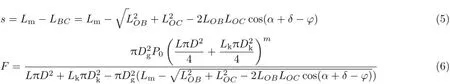
由第二类拉格朗日方程可得悬架系统的运动微分方程

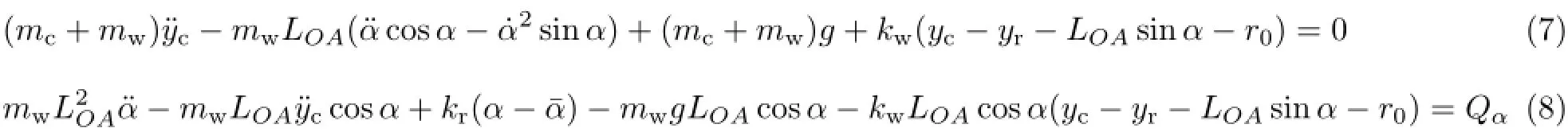
式中，g为重力加速度，mc为车体质量，mw为负重轮质量，kr为扭杆扭转刚度，Qα为由空气弹簧与电机作动器所产生的广义外力

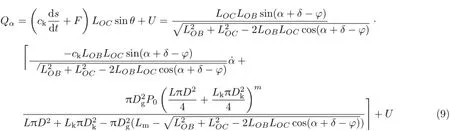
式中，U为电机作动器所产生的主动控制力矩。

由方程式(7)和方程式(8)可得系统静平衡方程

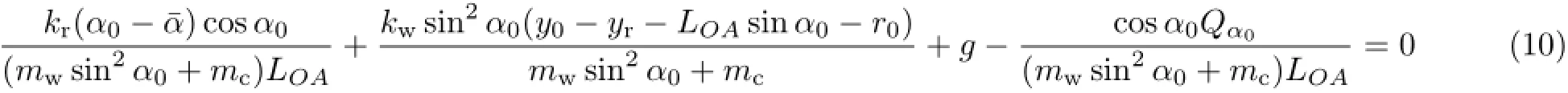
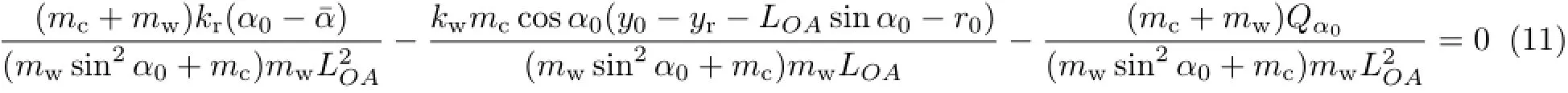
式中，y0与α0为系统静平衡时候车体垂向位移和扭杆转角，可由方程式(10)和方程式(11)求解得到；Qα0为静平衡时的广义外力。

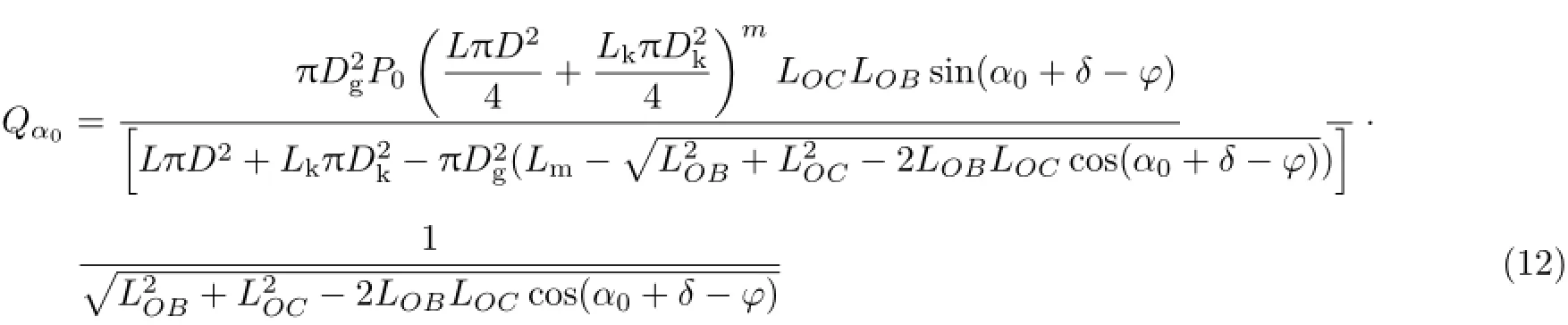
将方程式(7)和方程式(8)与方程式(10)和方程式(11)相减可得悬架系统的振动方程

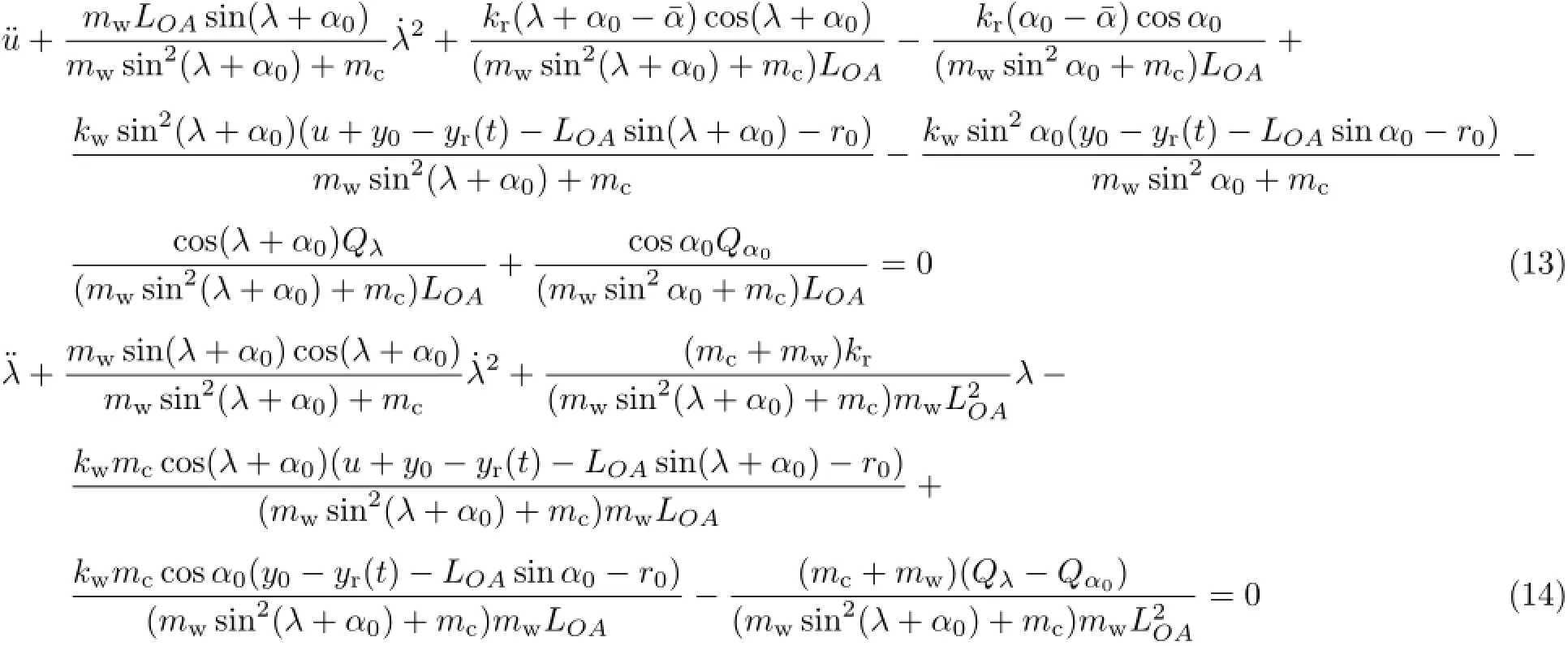
式中，u=yc-y0为车体垂向相对位移，λ=α-α0为扭杆相对角位移。Qλ为

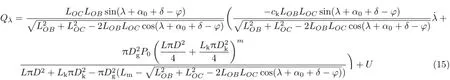
方程式(13)和方程式(14)中，yr为路面不平顺随机载荷。可以看出，悬架系统实际上是一个受控的随机激励的强非线性系统。本文主要目的是根据动态规划原理设计一个控制规律来对该系统的非线性随机振动进行有效控制。

2 非线性随机最优有界控制

路面不平顺载荷模型化为一个随机过程yr(t)，通常由路面不平顺谱描述其统计量

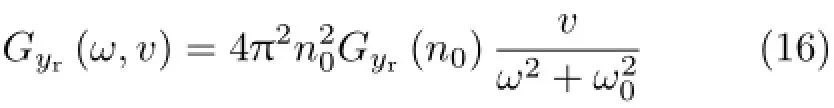
式中，ω0为最低截止角频率，n0为参考空间频率，v为车辆行驶速度，Gyr(n0)为路面功率谱密度。该不平顺通常可由一个高斯白噪声过程经一阶微分方程滤波得到

式中，W(t)为单位强度高斯白噪声。根据不同Gyr(n0)值可将路面不平度分为不同等级。

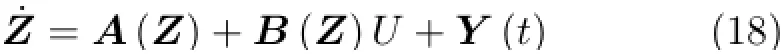
其中

实际运行过程中履带车辆所产生的电能是有限的，所以提供给每个电机作动器的电能也是有限的，从而导致作动器的执行能力受到限制。这个限制条件会影响实际控制力的执行效果，本文将设计考虑执行限制时的最优控制规律。设控制力的限制由如下约束描述

式中，Ud和Uu分别表示电机作动器的控制力下限和上限。

对于一个振动系统，以其振动响应最小为目标的最优控制通常用一个性能指标表示

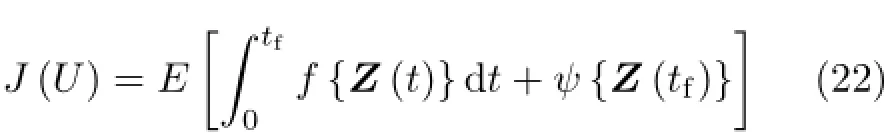
式中，E[·]为期望算符，tf为控制终时，f为成本函数，ψ为控制终值函数。f和ψ的函数具体形式由实际控制问题决定，对于线性系统的线性随机最优控制问题，f通常取状态向量的二次型。方程(18)～(22)构成了扭杆履带车辆机电悬架系统的非线性随机最优控制问题。

基于随机动态规划原理建立方程式(18)～(22)相应的动态规划方程

式中，V是值函数，tr[·]为迹算符，e为单位阵。

在限制条件(21)下对动态规划方程式(23)等号右边取极小值，从而得到最优有界控制力形式为

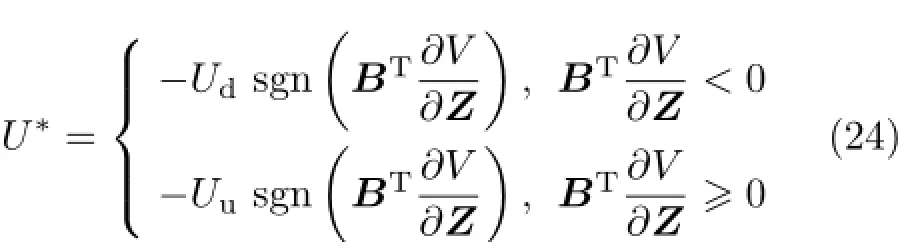
式中，sgn(·)为符号函数，其正负号由BT∂V/(∂Z)确定。可以看出，最优控制力是分段式非线性形式。

3 结果与讨论

对于12负重轮扭杆式履带车辆，机电悬架系统基本参数为：1/12车体质量mc=2000 kg，负重轮质量mw=100 kg，扭杆扭转刚度kr=20 kN·m/rad，扭杆预调角度¯α=0.53 rad，负重轮支承弹簧刚度kw=6.0×105N/m，负重轮支承弹簧原长r0=0.35 m。控制力下限Ud=-3000 N·m，上限Uu=3000 N·m，车辆时速v=25 m/s。

利用上述车体悬架和路面不平顺参数计算得到控制前后悬架系统的振动响应及其统计量，如图3～图5 和表2所示。

图3 (a)为被动与主动悬架车体垂向位移响应时程曲线。被动悬架是指电机作动器不起作用，仅在空气弹簧和扭杆弹性支撑作用下的车体响应，主动悬架是按式(24)确定的最优控制下的车体响应。可以看出，车体在主动控制下的垂向振动响应比被动下的振动响应有显著降低。图3(b)～图3 (d)分别为被动与主动控制下车体垂向位移、速度和加速度的频域(power spectral density，PSD)曲线。可以看出主动控

图3 控制前后车体垂向振动响应

图3 控制前后车体垂向振动响应(续)

图4 控制界限U对控制效果的影响

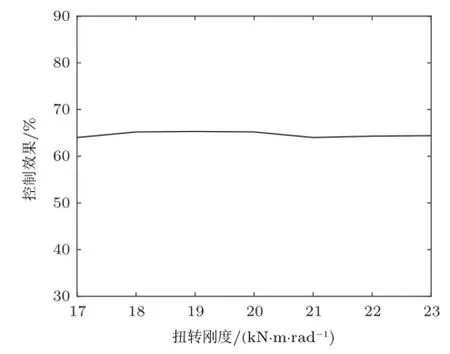
图5 扭转刚度对控制效果的影响

制力对车体在低频区间内的垂向位移、速度和加速度都有不同程度的降低。对于履带作战车辆而言，低频振动的抑制至关重要。车体垂向位移的降低有利于提高履带车辆行进间的打击精度，垂向速度的降低有利于提高履带车辆上载观瞄设备的观瞄精度，而垂向加速度的降低有利于提高成员的乘坐舒适度。

表2 不同路面等级下的控制效果

表2 显示了提出的控制策略在不同等级路面下对车体垂向振动的控制效果。控制效果用主动控制下车体垂向速度响应均方值相比于被动悬架响应均方值的减少百分比来衡量。可以看出，随着路面不平顺度的加强，履带车辆受到的随机载荷强度增加，控制方法的控制效果略有降低，但总体上能维持在60%以上。值得提出的是，我们假设在不同路面等级上电机作动器的执行能力是一样的，即具有相同的Ud和Uu值。图4显示了控制力界限|Ud|=Uu=U对控制力执行效果的影响规律。可以看出，随着电机作动器控制力界限的提高，控制力对车体垂向振动的控制效果逐渐增大。因此，在满足履带车辆其他部件能量供应后，适当提高电机作动器的电能供应或者更换更大作动力的作动器有利于提高控制效果。

实际履带车辆运行环境非常复杂，在运行过程中悬架系统的结构参数有时会发生改变。图5显示了扭转刚度变化对控制效果的影响。可以看出，在±3 kN·m/rad的扭转刚度变化范围内，控制效果也稳定在60%～70%。由此可见，提出的最优控制对于扭转刚度变化具有较好的鲁棒性。

在实际控制中，时滞现象是不可避免的，传感器采集和传递数据、作动器的作动过程均存在时间滞后。大量理论工作已经显示，控制力时滞对控制效果具有非常重要的影响。因此本文研究了时滞对车体振动控制效果的影响规律。根据式(18)建立含时滞的系统方程

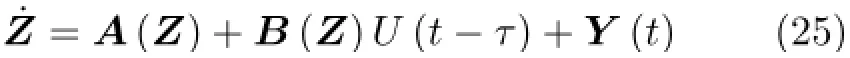
式中，τ为时滞时间。在其他参数不变的条件下对系统进行计算分析，得到时滞对控制效果的影响，如图6所示。可以看出，控制力时滞对控制力的执行效果具有很大影响。总体上，随着时滞时间的增加，控制力的控制效果逐渐降低。时滞时间小于0.15 s时，受控车体垂向振动均方响应随时滞变化比较缓慢，并且一直小于被动控制的均方响应，表明控制力还具有一定的控制效果。然而当时滞大于0.15 s之后，受控车体的均方响应快速增大，此时控制力不仅没有起到抑制振动的效果，反而导致车体振动响应增大。因此，提高传感器数据采集和作动器作动效率，减小时滞时间对履带车辆的主动控制具有重要意义。

图6 时滞对车体垂向位移响应均方值的影响

4 结论

本文研究了扭杆式履带车辆机电悬架非线性随机振动的最优控制。由于负重轮斜式放置和空气弹簧非线性，扭杆式履带车辆的悬架系统具有强非线性特征，在路面不平顺作用下会产生剧烈非线性随机振动。本文基于随机动态规划原理，确定了考虑电机作动器有界时车体悬架的非线性随机最优控制策略，并通过计算分析了最优控制力对车体垂向振动的抑制效果。主要结论如下：

(1)最优控制对车体垂向振动的位移、速度和加速度都具有不同程度的抑制作用，有望同时提升履带车辆行进间射击精度、设备观瞄精度和人员乘坐舒适度等。

(2)最优控制能适应不同等级的路面不平顺载荷，可以通过适当提高电机执行器的执行界限来提高控制的执行效果。

(3)最优控制对车体悬架参数的变化具有较好的鲁棒性，能在一定程度上适应复杂环境运行时履带车辆系统参数的不确定变化。

(4)时滞对控制力的执行效果影响较为显著，为保证控制力的执行效果，整个控制回路的时滞时间建议在0.15 s以内。

本文虽然只是针对单个悬架系统确定了随机最优控制策略，但是由于履带车辆的每个悬架都是独立控制的，因此，该控制策略可以应用到履带车辆的整车控制上，只是在整车控制时还需要考虑到整车电能在各作动器上优化分配问题。