数学活动：推动学生思维向更深处漫溯

摘要：数学活动作为一种独特的学习方式，既为学生提供了一条解决数学问题的新路径，又给学生创造了主体参与、积极探索、大胆实践、勇于创新的学习环境。“多边形的内角”和的教学通过组织学生开展实验探究性数学活动，引导学生进行观察、分析、判断、交流，在探索中归纳多边形内角和的计算方法，有效地培养学生的数学思维，发展学生的数学素养。

关键词：数学活动;思维发展;小学数学教学

中图分类号：G623.5 文献标志码：A 文章编号：1673-9094（2021）12A-0072-04

《义务教育数学课程标准（2011年版）》指出：学生学习应当是一个生动活泼、主动的和富有个性的过程。认真听讲、积极思考、动手实践、自主探索、合作交流等，都是学习数学的重要方式。学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。[1]数学活动作为一种独特的学习方式，既为学生提供了一条解决数学问题的新路径，又给学生创造了主体参与、积极探索、大胆实践、勇于创新的学习环境。大量成功的教学实践表明，在数学课堂中引进数学活动，不但能丰富数学的学习方式，而且更能有效地发展学生的数学思维，提升学生的数学素养。

一、丰富猜想活动，让思维起航

随着数字化时代的到来，数学越来越成为人们生活中不可缺少的工具。但在数学教学实践中，一些学生不喜欢数学，感觉数学就是做题，单调乏味，还有一些学生习惯于“老师让干什么就干什么”的机械式学习。数学活动是以“做”为支架的参与式活动，学生能感受数学，触摸数学，看到不一样的数学，从而变被动的“机械”学习为更加主动的“趣味”学习。数学活动也是以问题为链接点的连续活动，能诱发学生猜想，引发学生的思维冲突，让思维在猜想中萌发、起航。

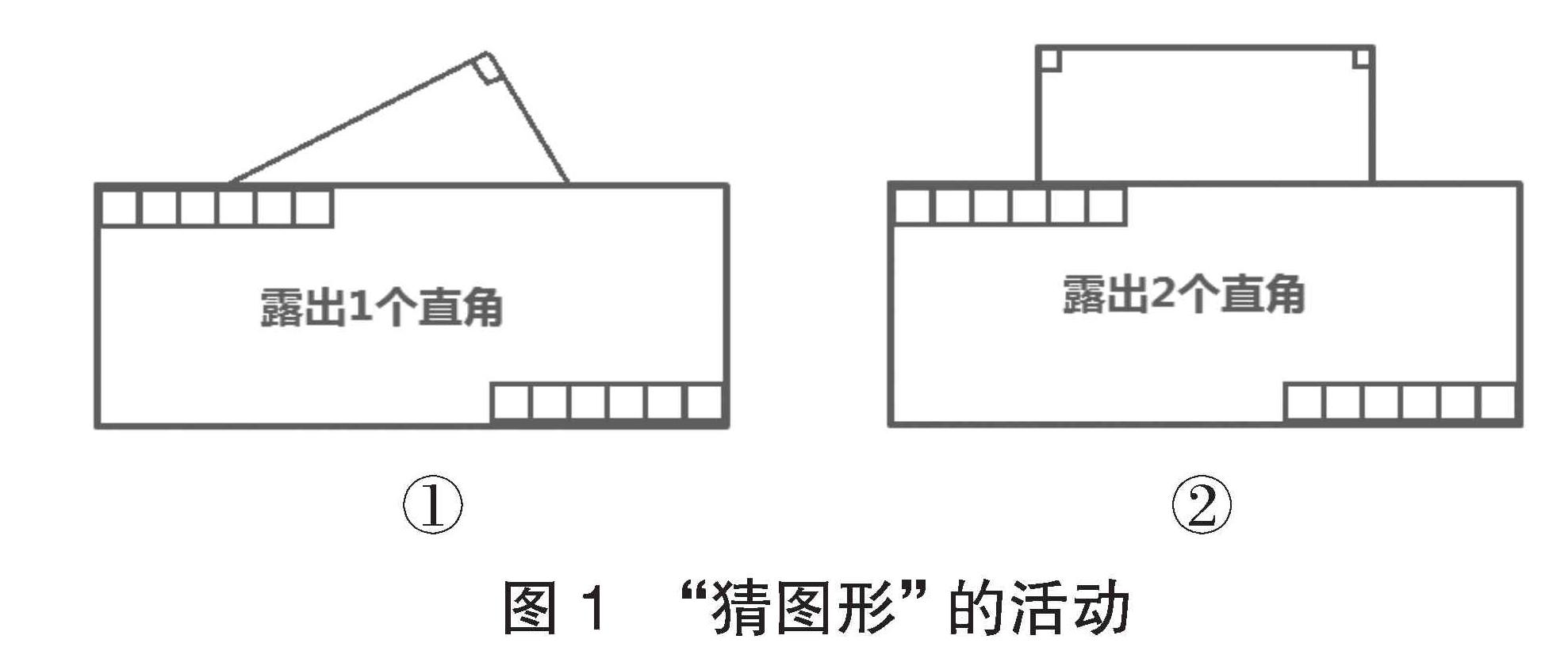
在教学苏教版小学数学四年级下册“多边形的内角和”时，笔者在课的开始组织了“猜图形”的活动（如图1）：

（1）教师手拿内有图形的信封，先露出图形的1个角（如图1-①），提问学生：“你们能够根据这个角，猜猜它是什么图形吗？”大多数学生猜是三角形，笔者顺势引导学生复习已经学过的关于三角形的知识。

（2）教师再把信封内的图形拉出来一点点，露出2个角（如图1-②），提问学生：“现在还是大家猜的三角形吗？”学生猜想：“露出了2个直角，不可能是三角形了！那会是什么图形呢？可能是长方形，也可能是正方形。”笔者继续提问：“那你们知道长方形、正方形的内角和是多少度吗？”学生已经掌握了长方形、正方形4个角都是直角，直角是90°的知识经验，得出长方形、正方形的四个直角内角和是360°。这个环节，完成了长方形、正方形这两个特殊四边形内角和的教学。

（3）教师继续提问：“信封内的图形到底是什么图形呢？让我们來揭开谜底：是一个直角梯形。直角梯形的内角和是多少呢？谁来大胆猜想一下？”

在“猜图形”活动中，笔者通过让学生猜露出1个角的图形，唤醒了学生的已有经验，同时也抓住了本堂课的认知起点——三角形内角和=180;通过猜露出2个角的图形，得出长方形、正方形这两个特殊四边形的内角和是90×4=360°;最后通过揭开谜底展开“研究一般四边形内角和”的教学。猜想推动着知识的辐射，使学生产生认知的不平衡，激发了学生要继续学习的迫切需求，让学生带着问题展开深入的探究，积极主动地参与到数学活动中去。

二、充实实验活动，让思维扬帆

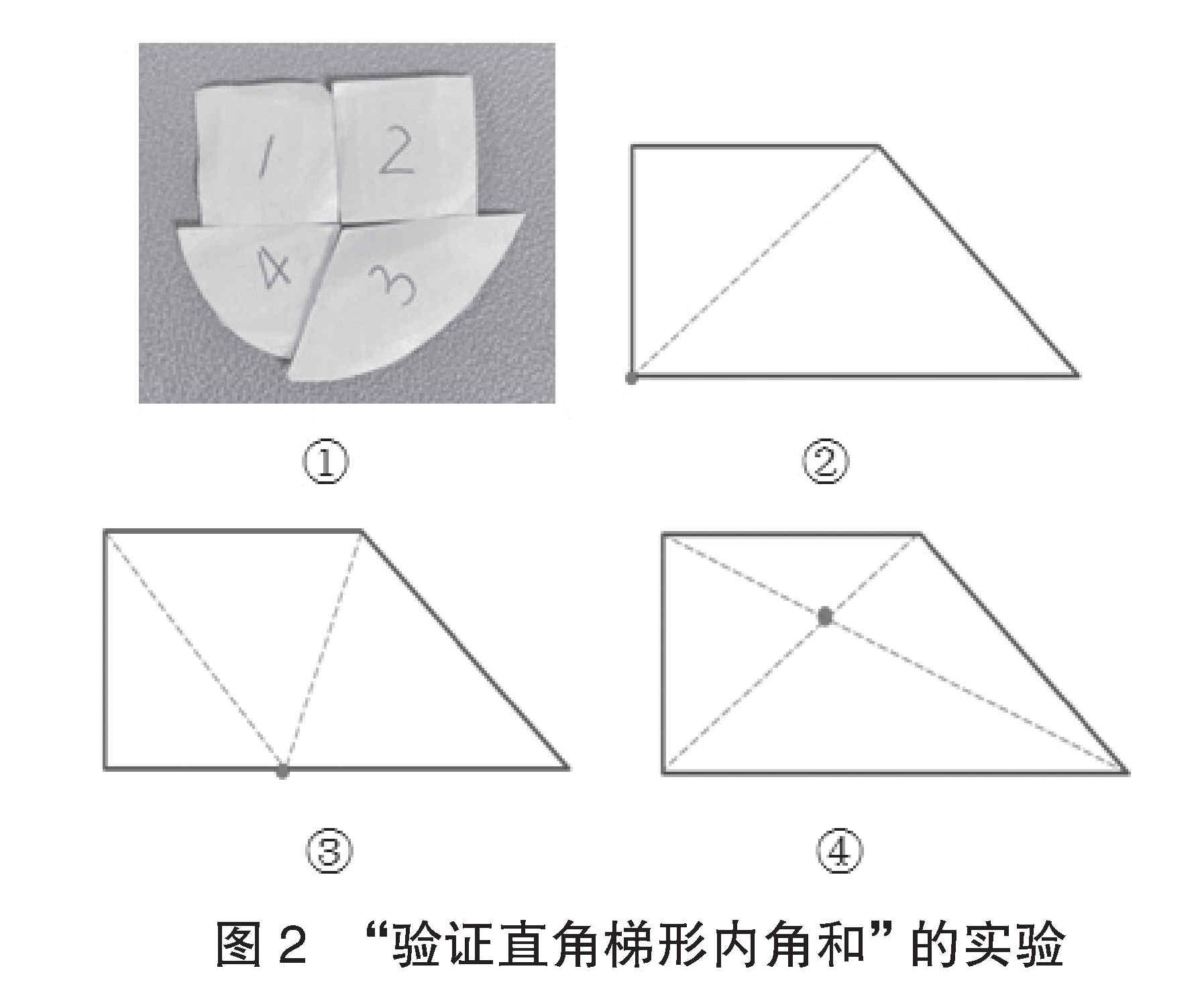
小学阶段的学生对所学知识往往处于一种似懂非懂的朦胧状态，而数学实验活动恰好能弥补这个“缺憾”。组织开展需要大胆猜想、动手操作、验证观点的实验活动，不仅可以让学生了解数学知识、规律，还能带领学生全面、深刻地体验学习过程和方法，使知识学习变得立体和丰富。数学实验不是盲目的，有了猜想，实验活动更有目的性，而为了验证猜想展开的研究活动，更像是一种验证性实验。有了科学研究的实验操作方式，学生的思维就不断灵活起来，越来越清晰有条理。笔者在教学“多边形的内角和”时，设计了“验证直角梯形内角和”的实验，请学生通过实验来证明“直角梯形的内角和是360 ”。在教师的引导下，学生的思维是发散的（如图2）。

“量”的方法最容易想到，用数据来说话，把4个内角度数加起来就是内角和度数;“拼”的方法最为直观，一目了然（如图2-①），把4个角剪下来拼在一起形成一个周角，一周角就是360 。根据学生的实验作品，教师引导学生尝试了另外三种分法。如图2-②，把直角梯形分成2个三角形，2个三角形内角和就是直角梯形的内角和360°，这种分法把直角梯形与三角形联系起来，实现了转化思考，充分开启了学生的思维。既然可以分成2个三角形，那能否分成3个三角形呢？学生在实验中发现，分成3个三角形，内角和就是180×3，但是比直角梯形内角和多了一个180平角度数，要减去，结果还是得到内角和是180×3-180=360°（如图2-③）。图2-④把直角梯形分成4个三角形，内角和就是180×4，但是比直角梯形内角和多了一个360周角度数，要减去，结果还是得到内角和是180×4-360=360°。

数学实验的本质是让学生在“动手做”的历程中挖掘思维轨迹，发现知识的本质。当“测量”“剪拼”“分成2个、3个、4个三角形”这些方法依次呈现时，学生的猜想得到了证实，方法得到了互补，思考得到了肯定，思维得到了碰撞。在与学生交流不同实验方法的过程中，笔者引导学生不断进行思考、修正、推理、想象，不仅让学生知道怎么做实验，还让他们知道为什么要这样做。

接着，笔者进一步引导学生观察后三种分法，深入地思考、寻找它们之间的联系：“三种分法都是把直角梯形转化成三角形来计算内角和的。分割的交点在内部（如图2-④）：4个三角形的内角和，跟原直角梯形内角和一样吗？多出了哪里？内角和是多少？分割的交点在边上：假如这个交点继续往下移，移到一个稍微特殊的地方，移到边上来呢（如图2-③）？现在分成几个三角形？内角和是多少？比原直角梯形内角和多了多少？分割的交点在顶点：这个交点继续移动，一直移动到了这个顶点上（如图2-②）。分成了几个三角形？内角和是多少？比原直角梯形内角和是多了还是少了？”学生认识到这个点落在了直角梯形不同的位置，有的在图形内，有的在边上，有的在顶点上，但不管在哪里，都能证明其内角和是360°。这一实验结果让学生非常兴奋，他们在思维达到高峰时还将这三种方法分别取名为“中心法”“边线法”“顶点法”。

我们往往会从不同的方法中总结出不同的规律，然而，不仅这些规律之间充满了关联，研究的方法和切入点也可以互相借鉴。充实的数学实验活动，给了学生更广阔的思考空间和研究视域，让他们的思维在课堂上活跃起来，提升了他们对数学的理解程度。

三、深入探究活动，让思维远航

数学课堂要尊重学生已有的经验，将丰富的现实情境引入课堂，鼓励学生提出自己的解题策略，促进同伴间的合作交流，使不同的人在数学上得到不同的发展。

在教学“多边形的内角和”时，笔者设计了“不同四边形内角和的探究实验”活动，让学生通过探究得出一组四边形（如图3）各自的内角和，并交流自己的研究方法。

学生先实验，再思考，然后交流不同的探究方法。有的学生用了顶点法，将四边形分成2个三角形，内角和是180×2=360;有的学生用了边线法，将四边形分成3个三角形，内角和是180×3-180=360;有的学生用了中心法，将四边形分成4个三角形，内角和是180×4-360=360。在原有数学知识学习的基础上，学生通过再次深入实验，操作探究，发现不管用哪种方法，都可以研究得出四边形内角和是360。

到这里探究还没有结束，笔者再抛出问题：“三角形的内角和是180，四边形的内角和是360，那么五边形、六边形、七边形（如图4），它们的内角和分别是多少度呢？有了研究四边形内角和的坚实基础，学生能自己设计活动进行研究了。随着探究的深入，学生不仅能发现其他多边形内角和度数的规律，还能对规律进行解释，并能掌握规律之间的联系。

从研究直角梯形的内角和发展到研究不同形状的四边形内角和，从研究四边形的内角和发展到研究五边、六边、七边等多边形的内角和，两个不同层次的探究活动，虽然在不同的探究任务下，但学生都是以发现者的身份去观察、猜想、实验、分析、推理、归纳，使数学活动成为再创造、再发现的过程。活动成果的展示不仅是结果的呈现，更是实验过程的回顾。学生在做中学、做中思、做中悟，實现向数学学习“智慧”层面的提升。

学生的数学活动经验是在亲身经历、实践、活动的过程中积累起来的。在实验成果展示的过程中，学生通过合作探究和交流，既展示自己的想法，回顾自己的探究历程，又能适时了解其他同学的学习方法。通过探究得到结论后的欣喜，将成为学生敢于实验、乐于探究的动力，使学生的思维在课堂上开出智慧之花。

四、感受活动魅力，让思维走向“创新”

数学活动涉及的内容是广泛的，在这些活动中既有可供学生思考、探究和具体动手操作的题材，也隐含着现代数学的一些原始生长点，让每一位学生都有机会接触、了解、钻研自己感兴趣的数学问题，满足学生的不同需求，最大限度地开启每一位学生的智慧潜能，让不同的学生在数学上得到不同的发展。

数学活动，可以让学生通过做、思合一，与生活相联系。在活动探索过程中，学生往往会有一种意犹未尽的感觉。根据学过的知识、运用实验得出的方法和积累到的活动经验进行深入的实验研究，是学生最感兴趣的事。这样的活动更具创新性、挑战性和综合性，能给学生带来更大的成功喜悦，让学生感受到数学的魅力。这样的数学学习，让学生不仅仅专注于本堂课的知识学习，还可以从本课知识出发，向更广阔的数学天地发展，从而激发学习的热情和创新的活力。“多边形的内角和”教学的最后，笔者抛出问题：“多边形随着边数的增加，内角和是不断变化的，而且是有规律地变化的。那外角和呢？它又有怎样的规律呢？”然后通过播放各种多边形内角和、外角和动态变化的小视频，引导学生感受多边形的外角和，激励学生利用多种数学活动进行学习，让学生带着问题走出课堂，体现了课堂学习的拓展性。课后的天地更广阔，学生可以根据自己的实践体验，用自己的思维方式进行知识的再创造，从中感受数学魅力，获得成功体验，产生学习数学的积极情感，提升归纳总结、灵活变通的能力。

学生在实操性数学活动中，通过实验探索和交流分享，思维不断向深处漫溯，不仅发现了多边形内角和的计算公式，还对知识的形成过程有了完整的了解，成为实验者、思考者、发现者。教学活动成为学生增长知识、发展思维、提升能力的过程，对学生当下和今后终身的发展都将产生积极的影响。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012：2-3.

收稿日期：2021-10-12

作者简介：袁绮蓉，江阴市辅延中心小学 （江苏江阴，214400），江阴市优秀教育工作者，江阴市教书育人标兵。