基于SVRGD的机载预警雷达自适应波束形成算法

彭 芳, 吴 军, 王 帅, 向建军

(1. 空军工程大学航空工程学院, 陕西 西安 710038;2. 空军工程大学空管领航学院, 陕西 西安 710051)

0 引 言

机载预警雷达通过测量目标的位置和运动特性,为作战系统和武器系统提供探测信息保障,是预警机完成空中警戒、控制引导、作战指挥与空战场管理等多样化作战任务的核心传感器。随着数字技术的快速发展,机载预警雷达正在由传统的模拟有源相控阵雷达向数字阵列雷达体制演变,在实现超低副瓣、低截获概率、提高强杂波背景中弱小目标检测能力、抗干扰能力等方面具有优良的性能[1-2]。接收数字波束形成是雷达数字信号处理阶段的一个关键流程,把阵列天线输出的信号进行A/D数字化后送到数字波束形成器的处理单元,完成对各种信号的复加权处理,形成所需的波束信号。该技术充分利用了阵列天线所获取的目标空间信息,通过信号处理使波束获得超分辨率和低旁瓣的性能,完成空域滤波以实现对目标的有效检测,以及对空间干扰信号的置零。波束形成有许多形式和算法,其中自适应波束形成算法[3-4]能适应各种外界环境的变化,可实时地将权值调整到最佳位置,对所要观测的目标能自适应形成一个很窄的主波束,对干扰方向自动形成零陷,以使干扰信号得到最大限度的抑制。

典型的自适应波束形成算法主要分为闭环算法与开环算法,其中闭环算法包括最小均方误差(least mean square,LMS)算法、差分最陡下降(difference steepest descent,DSD)算法、加速梯度(accelerating gradient,AG)算法以及这些算法的变形。这些算法相对简单,实现方便,但其主要缺点是搜索靠近极值时收敛变慢,可能会出现震荡,或出现局部最优化的情况,收敛速率受到系统稳定性要求的限制。波束形成算法的性能主要表现为稳健性、收敛速度、收敛精度等3个方面,针对非理想情况下的自适应波束形成算法性能下降问题,相关的稳健算法被陆续提出,如对角加载、特征子空间算法、不确定集算法和协方差矩阵重构算法等[5-6]。文献[7]中提出一种导向矢量和协方差矩阵联合迭代估计的稳健波束形成算法,计算复杂度较高。文献[8]中提出一种基于最小敏感度的广义线性自适应波束形成算法以适应低信噪比(signal to noise ratio,SNR)和小快拍数的应用环境,主要针对无线通信系统中的一类非平稳信号。文献[9]中将改进的粒子群算法应用于线性约束最小方差(linearly constrained minimum variance, LCMV)自适应波束形成器,在加深零陷和降低旁瓣等方面效果显著,但是对阵元数较多的高维复杂问题处理时容易陷于早熟和维度爆炸现象。

基于机载预警雷达上采用的三面阵天线结构,每个面的天线阵元数目多,针对传统LMS算法在短快拍数条件下导致波束形成性能下降以及因迭代震荡易收敛于局部最优值的问题,提出一种基于随机方差减小梯度下降(stochastic variance reduction gradient descent,SVRGD)的自适应波束形成算法,即在每一轮迭代的内部还有一个内部的迭代,在进行内部迭代前用当前的权值计算一次所有样本的平均梯度,利用全局的梯度信息对每次用于模型更新的梯度进行修正,通过缩减梯度估计的方差达到提高梯度计算准确性的目的,能有效改善波束形成和抗干扰的质量,亦适用于目标函数不可微和非平稳的情形[10-13]。

1 LMS自适应波束形成模型

1.1 面阵方向矩阵与接收信号模型

面阵列实际上可以看做线阵在二维空间中的拓展,如图1所示,假设均匀平面阵位于XOZ面内,阵列阵元数为M×N,水平方向和垂直方向的阵元间距分别为dx和dz,信源数为K。Θi=(θi,φi),i=1,2,…,K,θi和φi分别代表第i个信源的俯仰角和方位角,其含义如图2所示。其中,O≤θi<90°,O≤φi<360°。

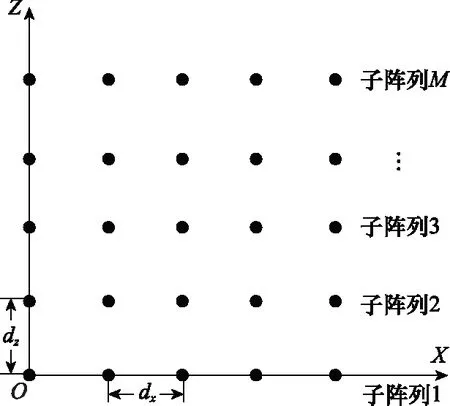
图1 均匀面阵列结构

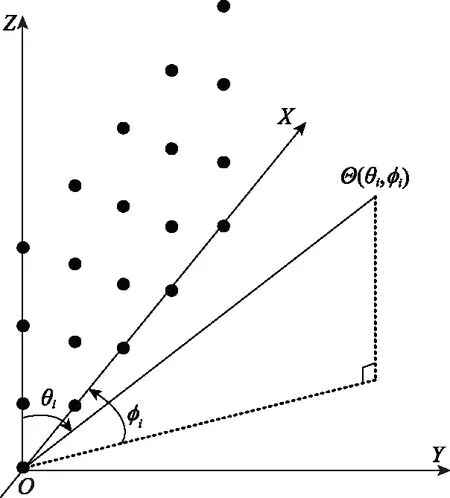
图2 均匀面阵入射角定义

以位于坐标原点的阵元为参考,在空间中第i个任意阵元与处于原点的参考阵元之间的相位差为

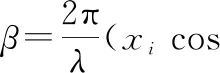
(1)

式中,(xi,yi,zi)表示第i个阵元的坐标;λ为入射信号的波长；φ为入射信号的方位角；θ为入射信号的俯仰角。由于yi的值为0,根据均匀直线阵的分析可知,x轴和z轴上的方向矩阵分别为

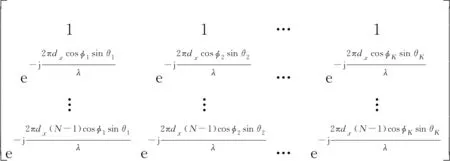
(2)

(3)

由图1可知,子阵列1的方向矩阵为Ax,而子阵列2的方向矩阵就得考虑沿Z轴的偏移,每个阵元相对于参考阵元的相位差就等于子阵列1的阵元的相位差加上-j2πdz·cosθ/λ,所以第M个子阵列的方向矩阵为AM=AxDM(Az),其中,DM(Az)表示由矩阵Az的第M行构造的一个对角矩阵。所以可得子阵列1～子阵列M分别表示为

(4)

面阵列的方向矩阵可表示为

A(Θ)=[A1,A2,…,AM]∈CMN×K

(5)

阵列接收信号模型为

X(t)=A(Θ)S(t)+N(t)

(6)

式中,S(t)是空间源信号,为K×1的列矢量；N(t)是阵元接收信号时的高斯白噪声,为MN×1的列矢量。

1.2 LMS自适应波束形成算法

LMS算法是一种基于LMS准则,采用标准梯度下降优化方法的迭代自适应算法,其代价函数为接收信号的阵列输出与期望信号的均方值,沿着代价函数的负梯度方向搜索,最终得到代价函数的最优解。

其优化问题可以表示为

(7)

式中,天线阵输出信号为y(n)=WH(n)X(n),其中X(n)∈CMN×L,W(n)∈CMN×1,L为快拍数;d(n)为期望信号。

将代价函数J(W)展开,有

J(W)=E[|d(n)|2]-2WHrxd+WHRxxW

(8)

式中,rxd是X(n)与d(n)的互相关矢量;Rxx是X(n)的自相关矩阵。采用标准梯度下降法求解式(7),即得LMS算法的权矢量更新公式:

W(k+1)=W(k)+2μe*(k)X(k)

(9)

式中,*表示共轭运算;μ为步长参数,当满足0<μ<1/tr(RXX)时,算法收敛。步长因子的大小影响收敛速度和稳态误差,固定的步长无法同时兼顾收敛速度和稳态误差的优良性能。

2 SVRGD波束形成算法原理与流程

2.1 SGD算法

在基于标准梯度下降的LMS波束形成算法中,每一步模型更新都需要计算所有样本点的梯度,对于样本数目比较多的时候代价较大。在机器学习领域,凸学习的目的是极小化代价函数,随机梯度下降(stochastic gradient descent,SGD)算法[9]作为一个更高效的算法,不要求基于精确的梯度值来更新迭代方向,而是通过取一个随机方向的步长,即每次随机从数据集中选择一个样本点it或者mini-batch进行梯度更新,保证在每次迭代时该方向的期望值与梯度方向是相等的。

给定L个训练样本(即快拍数),优化问题可表示为

(10)

极小化J(W)的SGD算法过程描述如下:

步骤1参数:标量μ>0,整数T>0

步骤2初始化:W(1)=0

步骤3fort=1,2,…,T

以一个分布随机选择vt,使得

E[vt|W(t)]∈∂J[W(t)]

(11)

更新

W(t+1)=W(t)-μvt

(12)

步骤4输出

(13)

相对于标准梯度下降,SGD算法的优势是不仅可以用于代价函数不可微的情况,还可以减少每次更新的计算代价,但是增大了梯度估计的方差,因此通过迭代输出取平均的方法可以改善收敛速度[14-16],但仍不如标准梯度下降。

2.2 SVRGD算法

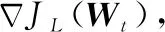
(14)

(15)

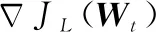
本文中,采用平均策略将每一次外循环中的所有内循环快拍产生的权矢量取平均,作为下一次外循环迭代的初始值,采用平均策略的好处是,当权值优化迭代越靠近全局最优值时,可能会在最优权值附近产生振荡,取平均后可以逼近最优解,提升收敛速度。算法过程描述如下:

步骤1初始化Wt(1)=0、Wj(1)=0;

步骤2fort=1,2,…,T;

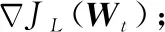
(16)

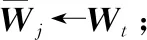
步骤5forj=1,2,…,J;

步骤6从集合{1,2,…,L}中随机选择ij;

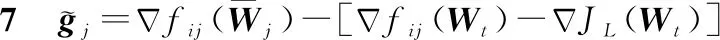
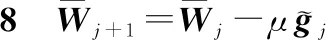
步骤9end for

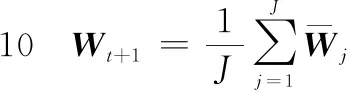
(17)

步骤11end for

2.3 基于SVRGD的自适应波束形成算法流程

利用式(5)和式(6)构建XOZ面阵接收信号数据模型,自相关矩阵用下式进行估计:

(18)

迭代步长μ满足0<μ<1/tr(RXX),以保证基于梯度、随机梯度的自适应波束形成算法收敛,其中tr(RXX)表示矩阵的迹。基于SVRGD的权值迭代算法具体流程如下:

步骤1设定算法内循环和外循环的迭代次数J和T,初始化外循环和内循环的权系数Wt(1)=0、Wj(1)=0;

步骤2进行外循环,由式(16)求取全体数据的平均梯度,其中e(k)可用式(7)求出;

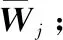
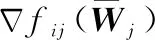
(19)

(20)

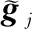
步骤7重复迭代步骤4～步骤6,直到达到内循环迭代次数J,利用式(17)计算平均权系数,并将其赋值给外循环;

步骤 8重复步骤2～步骤7,输出最后一次外循环的权系数WT作为自适应波束形成的最优权系数;

步骤9计算阵列的输出y(n)。具体公式如下:

3 算法仿真与分析

原始数据设置如下:M=16,N=16,λ=0.1 m,dx=dz=λ/2,θ0=90°,φ0=90°。

3.1 X-Z轴向均匀面阵方向图特性分析

对所有阵元加权的输出相加后得到阵列的输出,取模值并归一化后形成空间指定波束方向图,如图3所示。

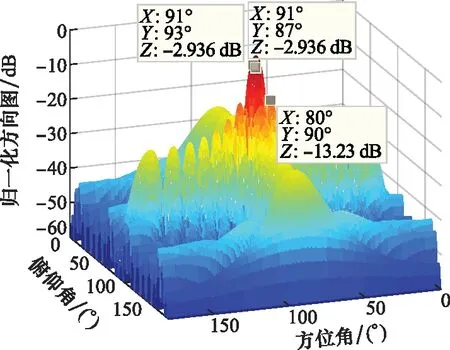
图3 16×16垂直向均匀面阵三维方向图

由图3可见,阵面为对称分布,方位角与俯仰角的静态方向图完全一致,波束主瓣宽度为θ3 dB=φ3 dB=6.42°,第一旁瓣位于80°附近,旁瓣电平为-13.23 dB。

3.2 SVRGD算法波束形成与抗干扰性能分析

将SVRGD算法与SGD算法以及传统的LMS算法的波束形成与抗干扰性能进行对比分析。

设定3种算法的迭代步长μ的取值均为1/[4tr(RXX)],满足收敛条件;目标信号是中心频率为3 GHz,带宽为5 MHz的线性调频信号;干扰源和噪声均为高斯白噪声,SNR为0 dB,干噪比(jammer to noise ratio, JNR)为10 dB;快拍数L=280;内循环次数J=L;外循环次数T=5;目标方向的俯仰角和方位角均为(90°,90°),两个干扰源的俯仰角和方位角分别为(90°,60°)和(90°,100°);设定俯仰角为90°，对方位角进行0°～180°的扫描,对阵元间距为0.05 m的16×16均匀面阵进行仿真得到水平特性波束方向图,如图4所示。

从图4可以看出,3种算法在目标方向(方位角90°)都形成了主瓣,主瓣宽度基本相同,在两个干扰方向(方位角为60°和100°)上都形成了零陷,其中SVRGD算法对于干扰的自适应调零要明显优于LMS和SGD两种算法。

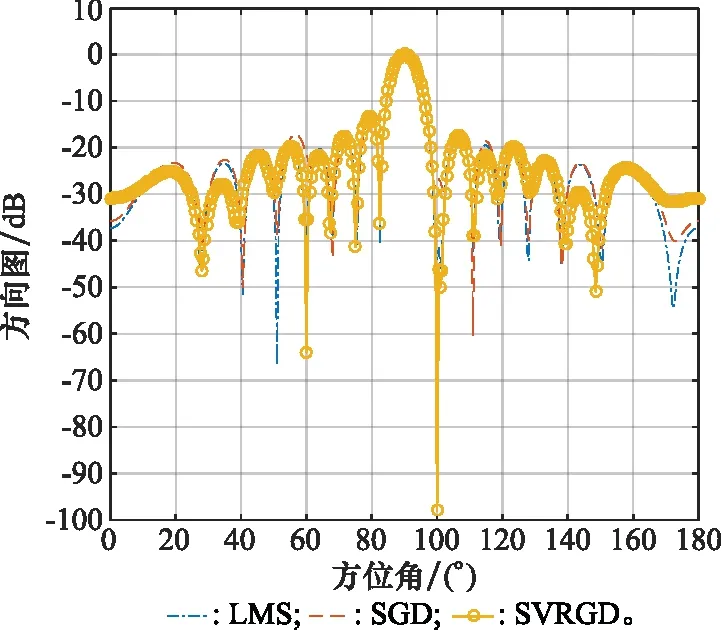
图4 俯仰角为90°的水平特性波束图

在其他条件不改变的条件下,JNR增加至50 dB,得到的仿真图如图5所示。

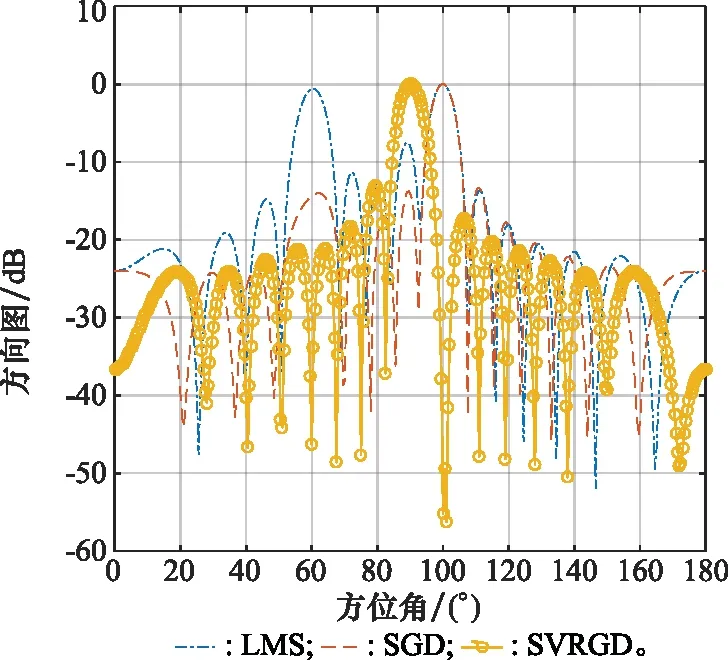
图5 JNR=50 dB的水平特性波束图

从图5中可以看出,由于干扰功率过强,在干扰方向上LMS算法以及SGD算法已经无法形成零陷,甚至形成了虚假旁瓣,而SVRGD算法依旧可以形成零陷,可以得知,SVRGD算法相较于LMS算法和SGD算法在对抗干扰方面有很大的优势。

在其他条件不改变的条件下,将JNR值在[-50， 50]dB区间范围内均匀采样,对3种算法分别求其均方误差,得到相应的变化曲线如图6所示。可以看出,3种算法估计的均方误差随JNR的变化趋势基本相同,即随着JNR的增大而振荡增加,在0～20 dB之间增幅显著。其中,JNR在10 dB以下时,LMS算法和SVRGD算法的均方误差值较小,SGD算法的均方误差较大。JNR在20 dB以上时,SGD算法的均方误差相对较小。LMS算法和SVRGD算法在整个区间的均方误差比较接近。

3.3 快拍数对SVRGD算法影响分析

在其他条件都不改变的情况下,将快拍数改为20时,得到水平特性波束方向图,如图7所示。

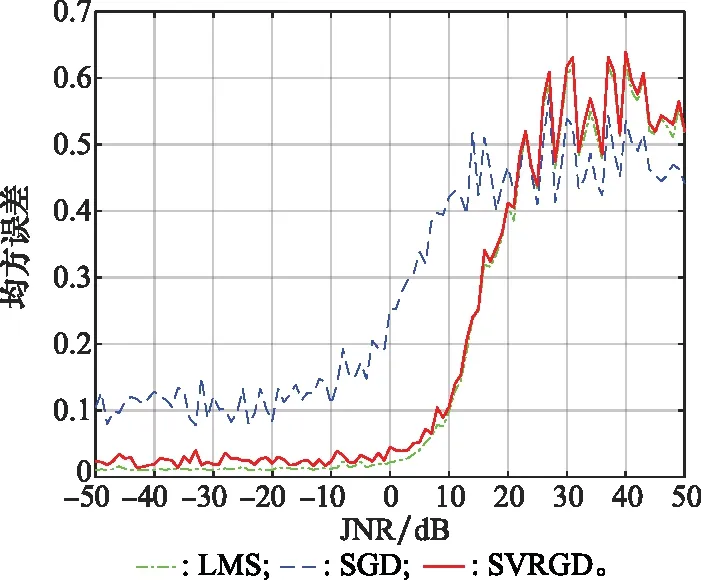
图6 不同JNR值对3种算法的影响

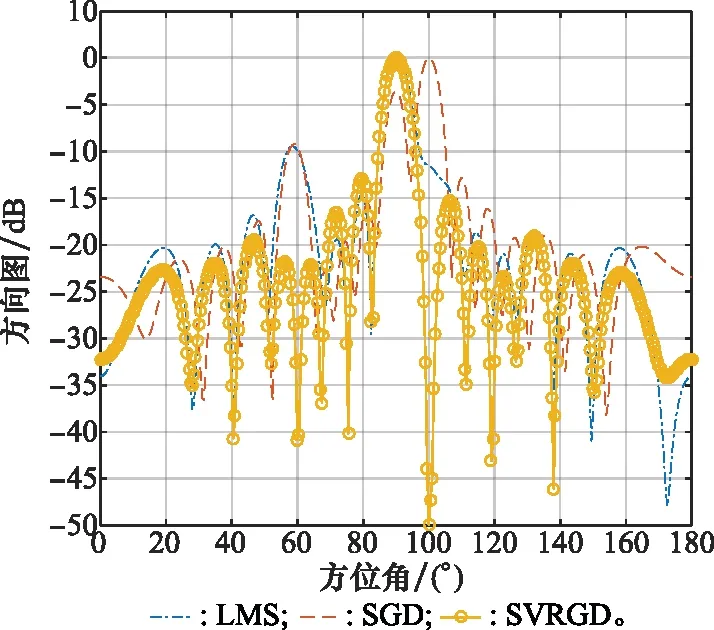
图7 快拍数为20的水平特性波束图

从图7可以看出,当快拍数过小时,LMS算法和SGD算法无法形成零陷,而且SGD算法形成的主瓣方向也发生了较小的偏移。但是SVRGD算法依然可以正常形成主瓣和零陷,与图4相比,在方位角为60°和100°的两个干扰方向所对应的幅值分别下降至-40 dB和-50 dB,零陷较前减轻。由此可见,对于快拍数较小的情况,SVRGD算法在期望信号波束指向和干扰方向自适应调零上依然具有较好的性能。

在其他条件不改变的条件下,将快拍数值在[20, 1 000]范围内均匀采样,对3种算法分别求其均方误差,得到相应的变化曲线如图8所示。可以看出,3种算法估计的均方误差都是随着快拍数的增加而振荡减小,其中SGD算法的均方误差在绝大多数区域内要大于另两种算法,LMS算法和SVRGD算法在整个区域内的均方误差比较接近,但在快拍数为300之内时,SVRGD算法的振荡幅度要大一些。

3.4 抗噪性分析

在其他条件不改变的情况下,将SNR由0 dB减小为-30 dB,得到的水平特性波束图如图9所示。在图9中可以看出,SNR过小时,对3种算法都会有很大的影响,SGD算法和LMS算法已经无法在目标方向形成主瓣而且无法在干扰方向形成零陷,但是SVRGD算法虽然旁瓣变高了,但是依旧可以形成指向准确的主瓣和零陷,因此SVRGD算法在抗噪声干扰方面也有很大的优势。

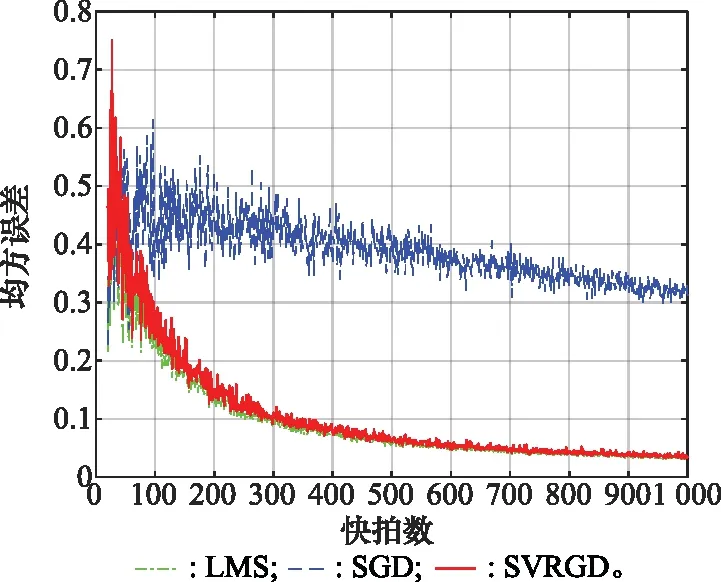
图8 不同快拍数对3种算法的影响

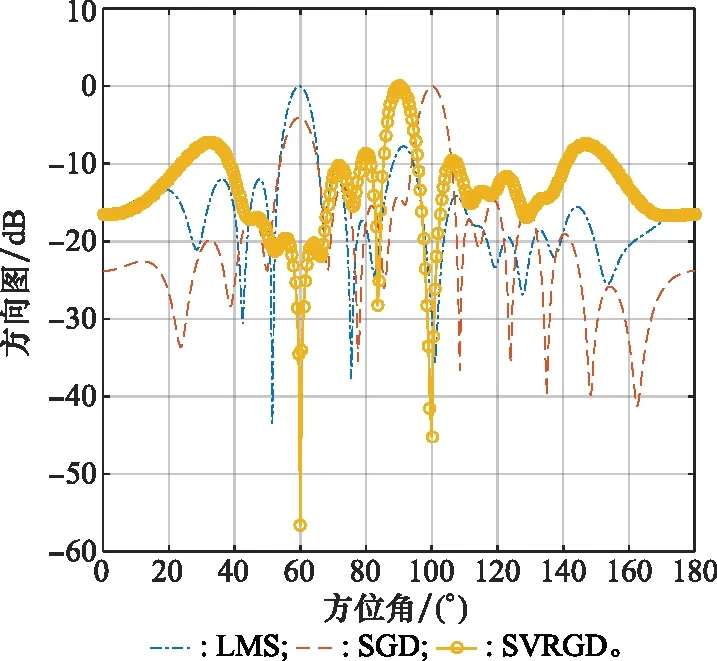
图9 SNR=-30 dB的水平特性波束图

在其他条件不改变的条件下,将SNR在[-40， 20]dB范围内均匀采样,对3种算法分别求其均方误差,得到相应变化曲线如图10所示。可看出,3种算法在SNR低于-10 dB时,均方误差曲线基本重合,且平坦趋于零;SNR在-10～10 dB区间时,LMS算法和SVRGD算法性能相当,SGD算法的均方误差随SNR增加的幅度较大;SNR在10 dB以上时,随着SNR的增加,3种算法的均方误差都随之增大,SGD算法增加得最快,SVRGD算法其次,LMS算法最慢。

虽然,前面分别讨论了JNR、快拍数、SNR等因素对3种算法均方误差的影响,其中LMS算法的均方误差值均略小于SVRGD算法。但是,均方误差的大小并不能完全等同于波束形成性能的好坏,算法性能通常会受到快拍数、收敛速度、循环次数等因素的综合影响,因此虽然LMS算法在单参数改变时均方误差性能较好,但是SVRGD算法的波束形成性能总体要优于LMS算法。

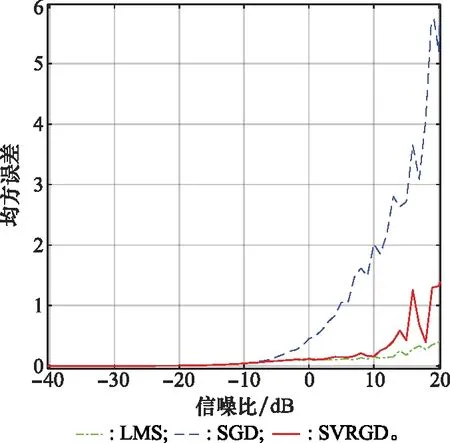
图10 不同SNR对3种算法的影响

3.5 收敛性能分析

仿真参数设置与第3.2节相同,3种算法的收敛速度如图11所示。

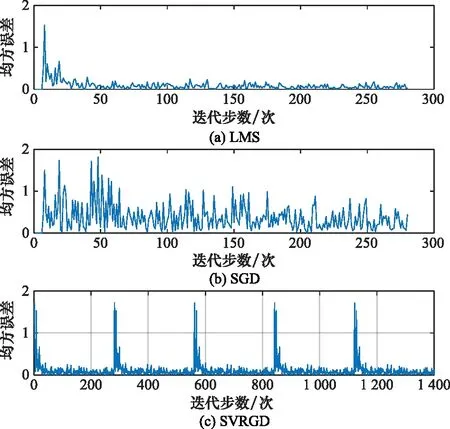
图11 3种算法的收敛速度图

由图11可以看出,3种算法中收敛性能最优的是LMS算法;SGD算法虽然因随机采用某次快拍数据估计梯度以代替标准梯度,其运算时间会变快但是其收敛速度比较慢,e2(n)随迭代步数的数值振荡幅度远大于LMS算法;SVRGD算法由于采用内外循环的方式进行权值迭代,运算时间不如LMS算法和SGD算法快,但是SVRGD算法在内循环中e2(n)随迭代次数变化情况与LMS算法相当,收敛性能明显优于SGD算法,这主要是由于内循环中输出的是平均权系数,这些较复杂的平均策略可以提升收敛速度,只是由于每次内循环结束之后,需要计算下一次外循环(总共5次外循环),然后重新进入内循环开始计算,导致方差瞬间变大,因此出现了每次趋于平稳之后又会出现尖峰的情况。

4 结 论

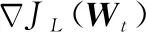
(1) 具有优良的波束形成能力和旁瓣抑制能力;

(2) 具有很强的抗干扰能力,对干扰方向能自适应调零,零陷较深;

(3) 在快拍数较少的情况下,由于采用内外循环的机制,使得波束形成仍具有较好效果;

(4) 在SNR很低的环境中仍然可以正常工作,波束保形能力好,具有较强的稳健性。

该方法的主要缺点是,由于内、外循环的迭代方式增加了计算量,使得该方法的计算速度和收敛速度不及LMS算法。通常,外循环次数的选择对算法性能影响较大,外循环次数越多,波束形成的精度越高,但是计算的复杂度也越高,因此需要在波束形成效能和算法实时性方面进行折中考虑。在实际工程应用中,如果将面阵进行子阵分块,采用SVRGD算法计算各子阵的阵列输出,再合成整个阵面的方向图,在保证优良波束性能的同时也大大节约了计算时间,具有较高的应用前景。