水声探空动目标参数测量方法
2021-01-05石海杰李京华
石海杰, 李京华, 陈 刚
(1. 西北工业大学电子信息学院, 陕西 西安 710129;2. 中北大学信息与通信工程学院, 山西 太原 030051;3. 中国联合网络通信有限公司东营市分公司, 山东 东营 257000)
0 引 言
水下探测空中声源在军民领域都得到广泛关注,特别在军事领域更具有重要意义[1-5]。潜艇是现代海军重要装备,其在近岸防卫、突破封锁、侦查掩护以及战略威慑等方面都有重要作用。潜艇在国防领域的突出作用必然伴随各种反潜技术的出现和发展,航空反潜是现代反潜技术中的重要方式。由于其具有机动灵活、通讯方便、协作迅捷的特点,航空反潜一直是空潜对抗中优势一方,为了提高潜艇的生存能力,水下对抗反潜飞机成为值得研究的课题。
航空反潜多采用螺旋桨飞机或直升机,这类飞机噪声中含有螺旋桨转动产生的线谱信号。线谱信号具有频率较低、功率集中、稳定性强的特点,可以传输到较远距离,是声探测设备检测和识别目标的主要信息载体。当反潜机以一定高度匀速通过水面上方时,水下声探测设备接收的信号将会产生多普勒频移,其中包含目标速度、距离、通过时刻等参数的信息,这为目标运动参数的测量提供了可能。
利用声信号多普勒频移特征,在单一介质中进行参数测量的方法已有较多研究[6-11],其中,Gomez -Tejedor[6]利用多普勒效应分析了4种直线运动,分析结果与实际运动状态有较好的一致性;Lindgren[7]利用声传感网络获取空气中目标的多普勒信号,采用改进的高斯牛顿迭代法解决最小二乘最优解问题,取得较好的定位效果;Timlelt[8]利用地面传声器接收过顶直升机多普勒声信号,估计声源频率和飞行速度等参数,在10 dB信噪比条件下取得了较高的估计精度;Statman[9]推导得到运动目标多普勒瞬时频率的解析表达,并采用最小二乘法进行参数估计,分析得出瞬时频率变化率与正横距离有较强相关性的结论;Xu[10]利用瞬时频率估计方法实现了水中目标的定位;Feng[11]利用时频分析方法测量水声多普勒信号的瞬时频率,该方法精度较高,但计算量较大。近年来,传感网络、数据融合、人工智能等技术在水声探测方法中的应用也是层出不穷,但多适用于复杂环境,实用性还有待验证[12-15]。以上方法均没有考虑声音跨界传输的问题,其结论亦不适用于水下探空的情况。Ferguson[16]和Lo[17]采用宽孔径水听器阵列,对空气中过顶飞行的直升机进行参数估计和定位。Buckingham[18]实测直升机过顶飞行数据,分别获取了空气中、海水中和海底沉积层中的声音信号,实测数据表明过顶信号具有时变特性,验证了在水中可以有效接收到空气中声源产生的多普勒频移信号,这满足了水下探空的前提条件。同时,水声探测设备的不断进步,也为水下探空提供了必要条件[19-20]。
在相关领域现有研究基础上,本文提出一种基于多普勒效应的单水听器探测空中运动目标参数的方法。通过理论推导、数据仿真、实测验证等途径,设计出一种算法简单,精度较高,能够实现速度、水平正横距离、通过时刻等运动参数测量的有效方法。
1 空中目标水声信号瞬时频率模型
声音由空气传入水中,会在空水界面产生反射和折射。由于二者声阻抗的巨大差异,只有入射角很小的声波才能传入水中,水下声信号好似由水面圆形小窗口引起,正如文献[21-24]中所述的虚拟声源。
空中点声源等高匀速运动模型如图1所示,图中描绘了空水界面之上频率为f0的声源,以速度v沿平行于空水界面的直线AB匀速运动,A′B′为AB在空水界面上的投影,也就是虚拟声源的运动轨迹,P为水听器所在位置,A″B″为AB在水听器所在平面上的投影,S为运动声源距离水听器的最近距离点(closest point of approach, CPA),S′为S在水面上的投影,水听器深度为d,声源高度为h,起始时刻声源与S点距离为l,虚源与S′点距离同样为l。由于声源与其对应的虚拟源具有相同的运动方式,因而具有相同的运动特征。
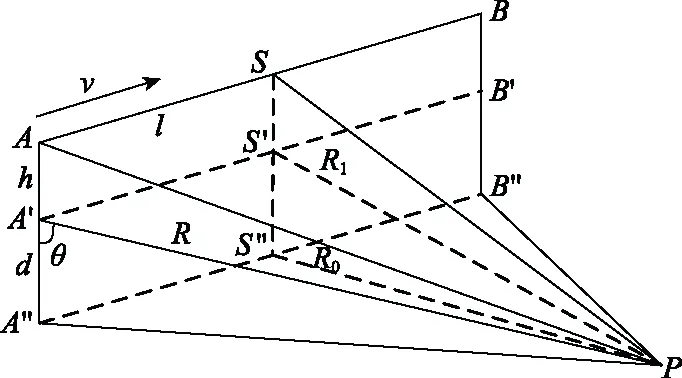
图1 空中目标运动模型
假设τ时刻,A′点处的声信号经过传输,在t时刻到达水听器处,则有
(1)
式中,cw是水中声速;R是τ时刻虚拟声源与水听器的距离,则有
(2)
式中,R0是目标的水平正横距离;d是水听器深度;R1是虚拟声源的正横距离;tc是目标通过时刻;v是目标速度。
将式(2)代入式(1)中,可解得
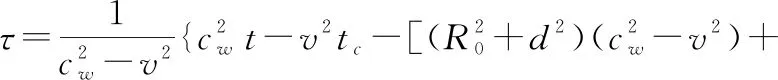
(3)
t时刻水听器接收的信号相位用z(t)表示,则τ时刻声源发射的信号相位2πf0τ再加上一个相位与z(t)相等。则接收端的瞬时频率f(t)[19]可表示为
(4)
由式(3)和式(4)联合可得
(5)
式中,f0、cw和d是已知量;v、R0和tc是被测量。可采用最小二乘法进行参数估计,但这种方法计算复杂,特别是在多参数联合估计时计算量比较大,本文将研究一种算法简单、精度较高、适合于工程应用的方法来进行参数的测量。
2 空中动目标参数测量
2.1 参数测量模型
本节将研究在已知声源基准频率f0的条件下,利用水听器所接收的信号,根据运动目标瞬时频率模型,测量目标运动速度v、通过时刻tc和水平正横距离R0(正横距离在水平方向上的投影)的方法。
由式(5)可以推导得到
(6)
(7)
式中,fa是声源从较远处接近水听器运动时信号的瞬时频率;fr为声源远离水听器运动时信号的瞬时频率。当目标距离CPA点较远时,可以认为fa和fr为固定值,由式(6)可得
(8)
由于fa可以在目标到达CPA点之前测量得到,因此参数v可以用来估计正横距离和通过时刻。将式(5)对时间求导,并假设v≪cw(直升机反潜作业时,其速度一般不会很高,而水中声速为1 500 m/s,这种假设是合理的),此时可得到等效源正横距离的解析表达式。
(9)
再根据水听器深度d可以计算目标水平正横离R0。
由式(5)可推知,目标在CPA点的频率fd(t)|t=tc=f0,假设t0时刻是水听器接收到信号频率f0的时刻,则得到目标通过时刻计算公式:
tc=t0-R1/cw
(10)
目标匀速通过CPA点,其多普勒频率变化是连续的,也就是在多普勒频率-时间曲线上,取CPA点附近的小段曲线可以近似认为是斜率为常数的直线。这就为在目标到达CPA点前一小段时间预测正横距离和通过时刻提供了可能。
在目标到达CPA点(tc时刻)前的某时刻t进行预测,得到正横距离为
(11)
t时刻预测的t0为
(12)
t时刻预测得到的通过时刻tc为
(13)
2.2 参数测量方法
根据以上推导过程,可以将基于多普勒效应的运动目标参数估计方法描述如下:
步骤 1开始。一经发现目标,开始对目标连续瞬时测频。测频时间间隔为T,fn为本次测频结果,fn-1为前次测频结果;
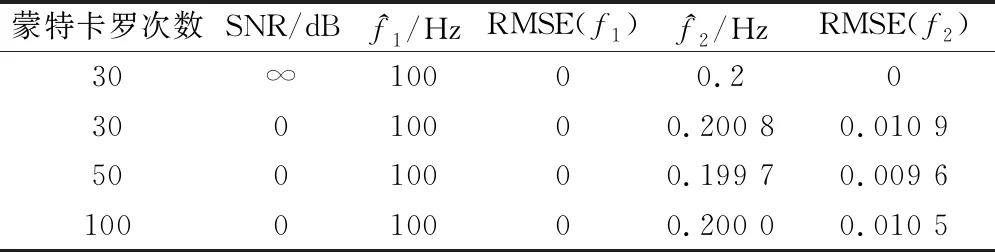
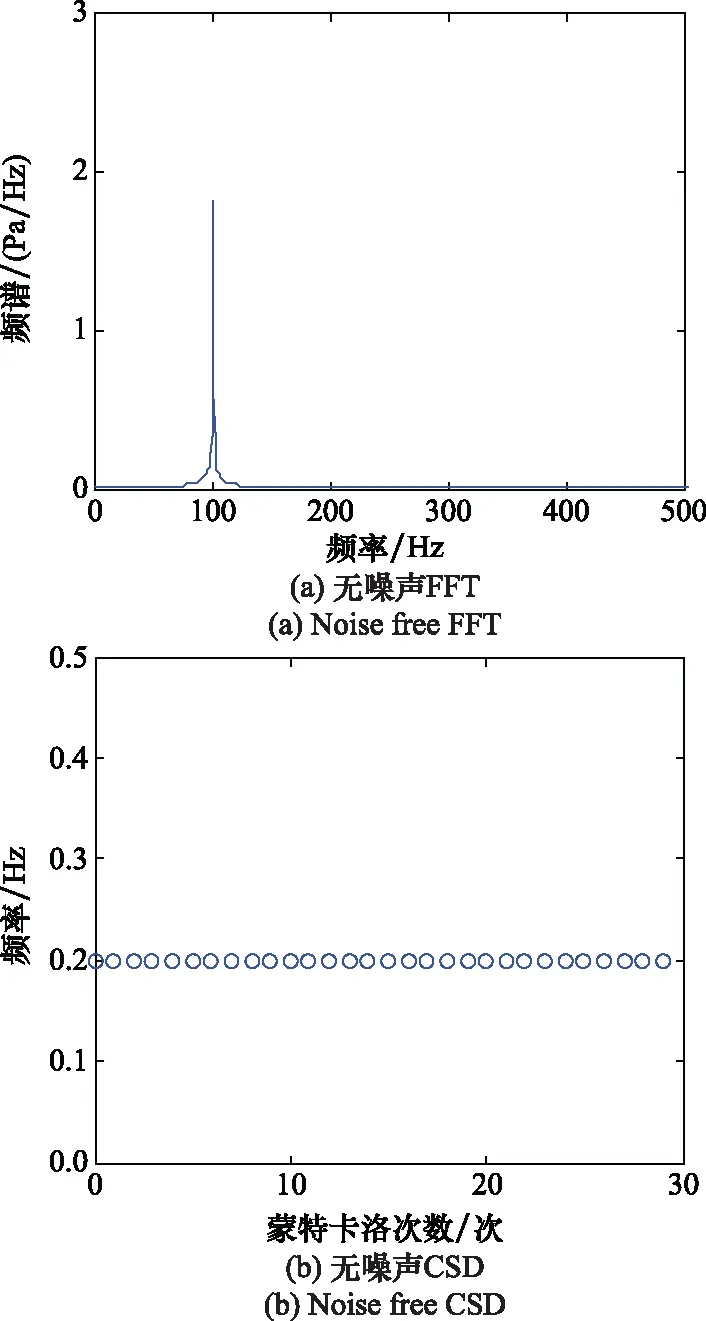
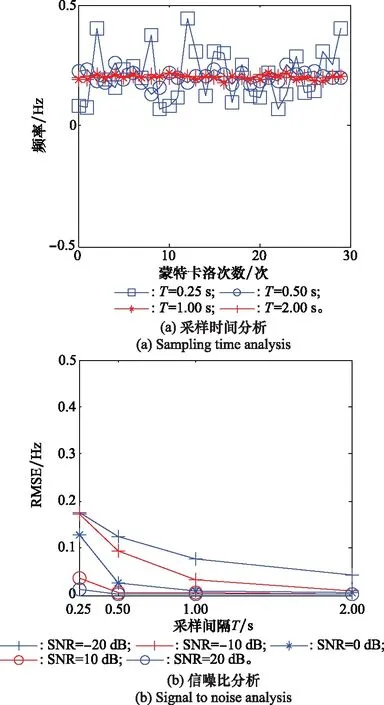
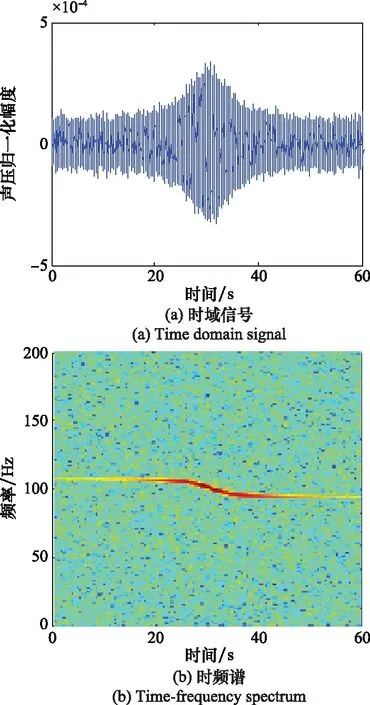
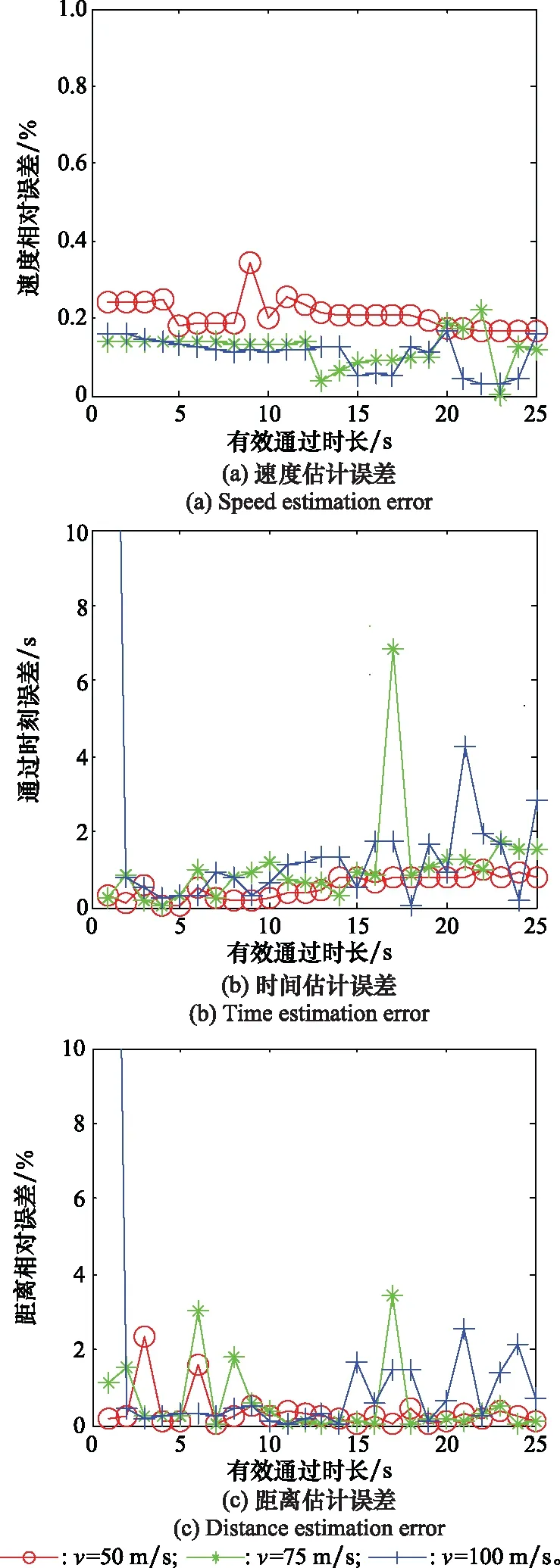
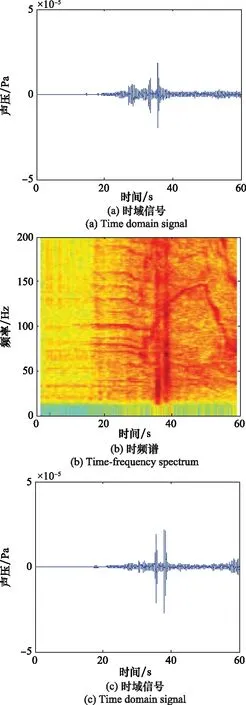
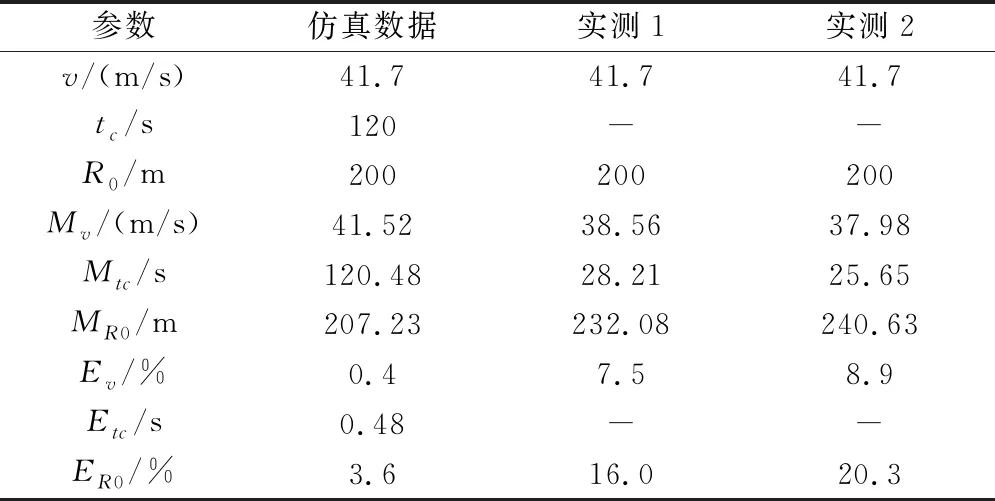
步骤 2估计fa。当满足一定条件时,fa=fn,判断准则为|fn-1-fn|/T 步骤 3估计速度v。根据式(8)估计目标运动速度v; 步骤 4进行运动参数估计。启动条件为|fn-f0|/T 步骤 5估计正横距离。根据式(11)计算正横距离R1,并根据水听器深度,计算水平正横距离R0; 步骤 6估计通过时刻。根据式(13)计算通过时刻tc; 步骤 7结束。 由以上的推导可知,本文所提出的方法依赖于对瞬时频率的估计,因此本节讨论适合在此应用的频率估计方法。基于快速傅里叶变换(fast Fourier transform, IFFT)类方法有诸多优势,但其频率分辨率受到采样时长的限制,在时变信号测量中不再适用。而以维格-威利分布(wigner-ville distribution, WVD)为代表的时频分析类方法由于算法复杂,计算量较大,无法满足实时性要求。针对以上问题,本文采用分段互谱密度(cross spectral density, CSD)的方法进行瞬时频率的估计。 对两段时间长度为T的相邻信号x1(t)、x2(t)采样,采样频率为fs,采样点数为2N。假设信号频率为f1+f2,其中f1=k0fs/N=k0/T(k0为整数),是通过傅里叶变换能够分辨的频率;f2 采样后的信号为 (14) (15) 两段信号的CSD可表示为 Y(k)=X2(k)·[X1(k)]* (16) 式中,[·]表示点乘;*表示共轭;X1(k)是x1(n)的傅里叶变换;X2(k)是x2(n)的傅里叶变换。根据维纳-辛钦定理,变换相关运算与傅里叶变换的顺序,可得 Y(k)=DFT{x2(n)·[x1(n)]*}=DFT[e-j2π(f1+f2)T]=DFT[e-j2π(k0+f2T)]=δ(2πf2T) (17) 根据式(17),可得 f2=arg max[Y(k)]/2πT (18) f1为傅里叶变换可分辨的频率,因此 f1=ser max[X1(k)]fs/N (19) 式中,ser max[]表示取序列最大值对应的序号。 根据式(19)和式(20),当给定两段相邻信号x1(n)和x2(n)时,其测频表达式为 f=ser max[X1(k)]fs/N+arg max[Y(k)]/2πT (20) 为了验证CSD算法的有效性,选取仿真频率为f1+f2=100.2 Hz的信号,采样频率fs=2 000 Hz,单次测频采样时长T=1 s,即傅里叶变换频率分辨率为1 Hz。其中f1=100 Hz是可以通过FFT分辨并测量的频率,f2=0.2 Hz是FFT无法分辨的频率,必须采用CSD方法测量。 18F-FDG PET/CT SUVmax与淋巴瘤患者临床特征及生物学指标的相关性(张玲芳)(12):1143 分别在无噪声和信噪比SNR=0 dB的条件下进行频率估计仿真实验,结果如表1和图2所示。表1所示为30次、50次、100次蒙特卡罗实验的估计均值和均方根误差。结合表1中f1估计结果和图2(a)与图2(c)可以看出,无论有无噪声,FFT均能测出精确到1 Hz的频率,说明FFT方法能够较好地估计信号的频率,但是其测频精度受到采样时长的限制,无法分辨出f2的存在。 表1 CSD方法测频结果 图2 CSD法测频仿真结果 结合表1中f2估计结果和图2(b)与图2(d)可以看出,CSD方法能够有效估计出f2=0.2 Hz的频率。同时也能看出CSD方法测频精度是受到噪声影响的,由图2(d)可以看出,当信噪比为0 dB时,测频结果在真实频率0.2 Hz附近有一定起伏。表1中f2估计结果表明,随着蒙特卡罗次数的增加,其估计均值逐渐接近于真实值,均方根误差(root mean square error, RMSE)基本维持在0.01 Hz量级,说明在0 dB信噪比条件下,CSD测频方法具有无偏一致性,测频精度可以达到0.01 Hz量级,是一种有效的测频方法。 分段CSD测频方法除了受到噪声影响外,还与单次测频采样时长有关,当采样时间过短时,噪声对于估计结果的影响将会严重。为了分析噪声和采样时间对于估计结果的影响,仿真了信噪比SNR=0 dB的条件时,不同采样时间对估计结果分布情况的影响。仿真结果如图3(a)所示。可以看出,采样时间越短,估计结果偏离真实值越大,估计结果越分散。同时仿真了在不同信噪比的条件下,估计结果的均方根误差随着采样时间变化的情况,仿真结果如图3(b)所示,可以看出,均方根误差随着采样时间增大而减小,随着信噪比降低而增大。从图3(b)中还可以看出,在采样时间T=1 s时,信噪比大于0 dB(包含0 dB)的信号,估计误差不大,明显好于信噪比小于0 dB的信号。 图3 CSD测频方法分析 由于实测数据受到海域、海况、季节、时间等多种因素影响,其信噪比等参数不稳定,难于准确测量,不适合定量分析。因而,采用仿真方法可以进行算法性能分析。快速场模型以波数积分方法为理论基础,是声波动方程的全波解,是一种适用于本文声场计算的数值仿真方法[25-26]。 假设空气、海水和海底都是均匀液体,声学参数为ρa=1.293 kg/m3,ca=340 m/s;ρw=1 023 kg/m3,cw=1 480 m/s;ρb=1 620 kg/m3,cb=1 806 m/s。其中ρ代表密度,c代表声速,下标a代表空气参数、下标w代表海水参数、下标b代表海底沉积层参数。仿真参数如表2所示,其中,h为声源高度,d是水听器深度,lcpa是声源的水平正横距离,v为目标速度,f0是声源频率,H为海水深度。 表2 数据仿真参数 仿真参数和前述环境声学参数如表2所示,利用Zhang[15]所述的基于快速场模型的运动目标水声信号产生方法,仿真空气中运动目标激发的水声信号,仿真过程中加入适当的噪声,最终的水听器接收信噪比为0 dB。仿真结果如图4所示,其中4(a)为时域信号,可以看出声源在中间时刻(30 s附近)有明显的过顶飞行过程;图4(b)是该仿真信号的时频图,可以看出在声源过顶飞行过程中产生了明显的多普勒频移。 图4 波数积分方法仿真水中接收信号 在第2.1节中,对运动目标参数测量方法做理论分析时,做了小段多普勒频率-时间曲线近似直线的假设,这种假设成立的条件受到正横距离和目标速度关系的影响。在单次测频采样时长确定的条件下,理论上来说,有效通过时长(R0/v)越长,相当于测频点越密集,小段频率-时间曲线更接近于直线,参数估计结果的精度就越高。但参数估计结果还依赖于相邻两个测点的频率差值,测点相邻过近时,单个频点的测频误差对估计结果影响增大。本小节将分析信噪比SNR=0 dB、采样时间T=1 s的条件下,估计误差与各参数间的关系。 图5所示为信噪比SNR=0 dB、采样时长T=1 s的条件下,速度分别为50 m/s、75 m/s和100 m/s时,速度v、通过时刻tc、水平正横距离R0的估计误差随着R0/v的变化情况。其中图5(a)是速度相对误差,图5(b)是通过时刻绝对误差,图5(c)是水平正横距离相对误差。 图5 估计误差分析 从图5(a)中可以看出测速误差受到有效通过时长(R0/v)的影响不大,这与实际情况相符。由式(8)可知,测速误差和目标与CPA点的距离有关,距离越远,fa越接近稳定值,估计误差越小。因此当仿真的数据时间越长,速度估计误差越小;而在实际工程中,如能在越远处发现目标,测速误差就会越小。 从图5(b)中可以看出通过时刻估计误差受R0/v影响,并且当R0/v的取值在5~15范围时,估计误差较小,超出这个范围,估计误差变大。正是由于估计误差同时受到直线近似误差、单点测频误差和频率估计间隔共同影响造成的。 从图5(c)中可看出水平正横距离估计误差同样受到有效通过时长(R0/v)的影响,并且当R0/v的取值范围为10~15时,估计误差有较小值。超出这个范围时,估计误差变大,特别是当R0/v的取值小于2时,误差显著变大。这是由于目标速度过快,有效通过时间过短,信号的多普勒频率变化在很短的时间内发生,而测频方法对瞬时频率分辨有限所致。 某次实测实验两组数据的时域图和时频图如图6所示。 图6 实测信号 实验采用的是某型号螺旋桨飞机,飞机飞行高度为100 m,以150 km/h的速度等高匀速飞行,通过水听器所在水域的上方,水平正横距离为200 m,水听器位于水下深度为15 m,两组实测数据命名为实测数据1和实测数据2。同时,按照第4.1节的仿真方法,假设飞机飞行速度v=41.7 m/s,水平正横距离为200 m,其他参数与第4.1节所述相同,仿真一组待测数据,命名为仿真数据1。 实测实验数据表明(见图6),没有飞机过顶飞行时的环境噪声信号幅度(见图6(a)0~20 s的时域信号)明显小于有飞机过顶飞行的信号幅度(见图6(a)20~40 s的时域信号),说明0 dB信噪比的假设是适合本文应用背景的。因此,本文在0 dB信噪比条件下对算法进行分析和验证,采样时间T取1 s。 按照本文的参数估计方法,对以上3组数据进行目标参数估计,单次估计采样时长T=1 s,估计结果如表3所示。 表3 测量结果 其中,v、tc和R0分别代表目标速度、通过时刻和水平正横距离的真实值,M代表估计值,E代表误差。由于实测数据的通过时刻没有参照,因此未做误差分析。对估计结果进行对比分析可得出如下结论。 仿真数据1的有效通过时长(R0/v)为4.79。仿真结果中目标速度、通过时刻和水平正横距离的测量误差分别为0.4%、0.48 s和3.6%;图5分析结果中,R0/v=4.79处3个参数的误差分别约为0.25%、0.3 s和1.0%。两者对比可以发现,估计结果与分析结果是相符合的,水平距离估计误差略大,这是由单次估计的随机性造成的。 两组实测数据的有效通过时长(R0/v)为4.79(受到实验电缆长度、实验飞机安全速度条件限制)。目标速度和水平正横距离两组数据的估计误差均值分别为8.2%和18.1%。相同条件下的仿真数据两参数估计误差分别为0.4%和3.6%。两者对比可以发现,实测数据估计误差大于仿真数据估计误差,这是由于实际海洋环境受到海域、海况和人类活动噪声等多种因素的影响,在没有做环境具体分析和校正补偿的情况下,其误差必然要大于受控的仿真情况。因此,海域、海况、人类活动等因素对于估计精度的影响是该方法应用于工程时必须要考虑的问题,也是作者在此后研究中将要关注的问题之一。 本文建立了一种利用水下声信号探测空中运动目标的模型,提出了行之有效的运动目标参数估计方法。通过仿真分析,得出参数估计精度受到有效通过时长(R0/v)影响的结论。利用运动目标瞬时频率模型,把正横距离点处的多普勒-时间曲线等效成小段直线,把目标参数估计问题转化为瞬时频率估计问题,使问题得以采用简单、有效的方法加以解决;采用分段CSD方法,提高瞬时频率估计精度,在满足实时性要求的条件下,提高了运动目标参数的估计精度。 本文方法在仿真的条件下取得了较高的估计精度,并通过实测实验对方法进行了可行性的验证。实际海洋环境存在各种噪声,如何提高在复杂海洋环境下本文所述方法的估计精度,是需要进一步深入研究的工作。3 瞬时频率估计方法
3.1 分段CSD方法理论基础
3.2 分段CSD算法仿真
4 仿真分析
4.1 数据仿真
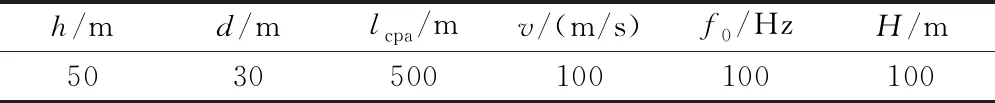
4.2 算法分析
5 实验验证
6 结 论
