电子侦察测频系统的建模与仿真

2015-12-20周志军

电子科技 2015年2期

周志军，祝婷

(西安电子科技大学电子信息攻防对抗与仿真重点实验室，陕西西安 710071)

现代战争条件下，电子侦察和电子干扰对抗日趋激烈，空间电磁环境信号空前复杂、密集且相互交迭，而所有这些信号都需要电子侦察系统接收，这给系统设计人员提出了更高的挑战［6］;所有这些信号都可以看作是瞬时输入带宽内覆盖多个不同带宽，不同载频的带通信号，它们在频域上相互靠近且互不重叠，需要电子侦察接收系统将其分离，并提取每个信号的瞬时特征，达到侦察的目的;而侦察的先决条件是测频，它是保障整个系统优良性及准确性的先决条件［7］。

1 信道化测频和瞬时测频模型概述

信道化测频就是将宽带数字信号送入一个多相滤波器网络，在网络中进行信道化频域均匀分割和抽取，输出若干个低速率子频带信号，子频带信号再经过频率测量，从而估计出各个子信道信号的频率范围［2］。信道化测频模型如图1所示。

图1 信道化测频模型

瞬时测频需要系统有良好的瞬时性，用较短的时间或较少的采样点估计出某个时间段的瞬时频率;工程意义上的瞬时测频是指在测频误差倒数量级时间段上的测频［3］。例如，对于测频精度为1 MHz，用来测频所占用的信号时间约为1μs或更小，则被称为瞬时测频。瞬时测频模型如图2所示。

图2 瞬时测频模型

2 信道化测频

2.1 基于多相滤波器组信道化模型

采用多相滤波结构，将大带宽分为多个子带，可以充分发挥多相结构并行运算和降速的优势［1］。经过多相滤波的第k路信道的输出信号为

式(1)中，xp(m)为经D倍抽取后的输入信号与多相滤波器的卷积，即

式(2)中，Sp(m)为经过 D倍抽取后的输入信号，hp(m)为经过D倍抽取后的滤波器冲激相应。基于上述理论分析，对多相滤波器组信道化模型的仿真结果如下。

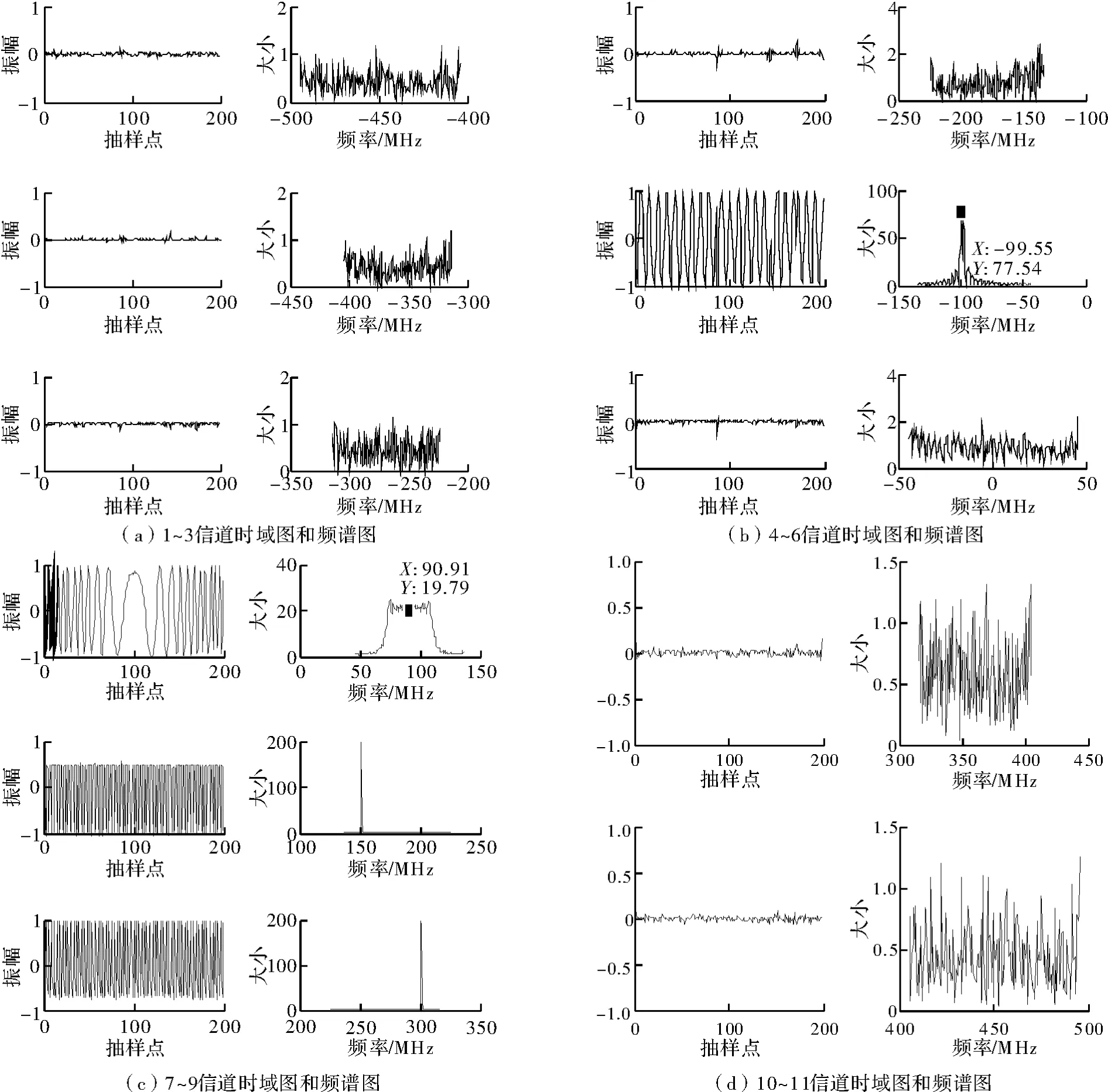
图3 11信道的信号时域图和频谱图

仿真参数选择:信道数D为11;采样率为990 MHz;信号脉宽为2.2μs;信噪比为20 dB;两个单音信号载频分别为150 MHz、300 MHz;调相信号载频为－100 MHz;线性调频信号中心频率为90 MHz，带宽为40 MHz。

由图3可知，信号落在5、7、8和9信道上，调相信号落在了第5信道，线性调频信号落在了第7信道，两个单频信号落在了8和9信道;其他信道上的能量很小;并且从图3(b)和图3(c)的标注也可以看出，调相信号和线性调频信号的中心频率偏差比较小，都在两个精度的范围内。从而说明信道化结构能够有效地分离多个同时到达的信号。可见，这种基于多相滤波的数字信道化算法，是一种高效的算法，对于高速采集的信号具有降速和下变频的作用，能够输出低速、下变频后的信号，这种低速信号使后续信号处理变得相对容易。

2.2 基于瞬时自相关的测频模型与仿真

利用信号的瞬时自相关函数来实现频率测量具有比传统方法更好的抗噪声性能［5］。计算瞬时自相关函数仅需对间隔m点的两个数作乘法，无需求和，因此具有较高的运算效率。设经过数字下变频和抽取后的复基带信号y(n)可以表示成如下正交形式［4］

其中，I(n)是同相分量;Q(n)是正交分量，可分别表示为

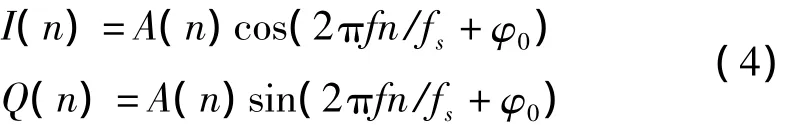
其中，A(n)为信号的包络;f为信号瞬时频率;fs为抽样频率;φ0为初始相位。信号y(n)的瞬时自相关函数可以表示为

由式(3)～式(5)可求得瞬时频率

其中，ΨR(n，m)= －arctan［sin(2πfm/fs)/cos(2πfm/fs)］。

由式(6)可以看出，瞬时自相关频率只与时延和输入信号频率有关［3］，和初始相位无关，并且只要满足≤fs/6m时就可以通过瞬时自相关函数的相位获得信号的无模糊瞬时频率。

基于上述理论分析，对经过数字信道化后的正弦信号，线性调频信号和调相信号进行瞬时自相关测频，并以单频信号为例在时延m取不同值时估计瞬时自相关测频的误差。

图4 时延m取不同值时瞬时频率估计及误差分析

仿真参数选择:在做基于瞬时自相关测频时，鉴于瞬时自相关算法的约束条件fs＞4·fmax·m的限制，之前选取的单频信号的载频不符合其约束条件，出现了频率模糊，因此这里将其中一个单频信号的载频改为10 MHz，使其落在第6信道，目的是为了在时延m取不同值时对其瞬时频率做误差估计。

如图4(a)所示，瞬时自相关算法能较准确地测出经信道化后的瞬时频率，且估计精度较高。图4(b)中的波形是经过放大后的波形，可以看出，在时延m取值越大时，其瞬时频率估计精度越高，主要原因是时延m越大，其抑制噪声的能力越强，测频精度改善的效果越明显，但时延m也不能过大，否则为避免频率模糊，需要相应地提高采样频率。

图4(c)是测频均方误差随信噪比和时延的变化情况，经分析可知，随着信噪比的提高，测量误差会减小，在信噪比＞20 dB时，不同时延情况下的测频均方误差均＜0.5 MHz，具有较高的测频精度。另外由于噪声的相关性差，信号的相关性强，求瞬时自相关函数后噪声会减弱，信号会加强，能在一定程度上起到抑制噪声的作用，提高测频精度，m越大这种现象越明显。

工程上m的取值不宜过大，一般在1～2之间，因为在这个范围内测频精度已经足够估计较为精确的频率，m值即使再大，估计精度也相差不明显，反而m值越大会增加计算量;m的取值不只对该测频模型有效，对其他测频模型也有效。

3 基于改进相位差分法的瞬时测频

3.1 传统的相位差分法

对输入连续复信号z(t)采样后变为离散复信号z(n)=A(n)ejφ(n)，对信号 z(n)并行分成两路进行操作［8］。其中一路做一个单位的延迟并取共轭，得到z*(n －1)=(A(n)ejφ(n－1))*，即 z*(n － 1)=A(n)e－jφ(n－1)，另一路信号保持不变;然后对两路信号做复乘，得到z(n)·z*(n－1)=a+j b，则可得到相位差，把相位差带入后向差分算子即可计算出信号的频率［6］。

相位差分法从理论上只需两个采样点即可估计出信号的频率，容易实现短数据实时测频的功能。

3.2 改进的相位差分法

传统的相位差分法测频有诸多劣势，估计精度较差，所以我们改进了传统的方法。根据不同时刻噪声的不相关性，利用多点平均，在一小段时间内对N个测频值取平均，其效果相当于测频精度的误差减小了N倍。

以4点平均为例进行说明。首先将输入来波信号X分别作1个单位、2个单位、3个单位、4个单位的时间延迟得到4路信号，分别为 X1，X2，X3，X4;然后从第4路开始对将每一路信号做共轭运算并与前一路信号相乘，得到相邻两路信号的相位差 Δφ1，Δφ2，Δφ3，Δφ4，根据公式便可得到测量的瞬时频率festi1，festi2，festi3，festi4;最后求出这 4 个频率值的平均值faver，该频率即为所估计的瞬时频率。由于不同时刻噪声的不相关性，根据误差公式可知，当对测得的频率取N点平均时，相当于估计误差相应减小N倍，从而测频精度得到提高。

以线性调频信号为例，分别采用无平均、4点平均、8点平均对频率进行测量;并相应的估计出测频精度，即测频误差曲线;图5是仿真结果。

图5 传统相位差分法与改进相位差分法的测频比较

仿真参数选择:采样率为300 MHz;信号脉宽为2μs;信噪比为20 dB;线性调频信号中心频率为100 MHz，带宽为50 MHz。

图5(a)是采用无平均的传统相位差分法的瞬时测频结果。图5(b)和图5(c)分别是平均点数为4和8时基于改进的相位差分法的测频的结果。图5(d)是3种测频后的估计误差。如图5(a)所示，传统相位差分法的瞬时测频在整个测频过程中频率波动较大。如图5(b)和图5(c)所示，采用多点平均的改进相位差分法测频频率波动较小且精度较高。如图5(d)所示，与传统相位差分法的瞬时测频相比，在同一噪声下，基于改进相位差分法的瞬时测频可以显著提高测频精度，减小均方误差。另外，当 SNR＞20 dB时，采用8点平均的改进相位差分法的测频均方误差已经＜1 MHz，该测频算法是可行的。实际应用中可以综合考虑信噪比，测频时间和测频精度要求等相关因素，来选取不同测频值的点数。

3.3 信道化测频和瞬时测频仿真数据对比

表1～表3为频率为10 MHz的单频信号在不同信噪比下做了100次MentoCarlo实验得到的信道化测频的仿真数据。其中，表1为在时延m=1时的测频数据;表2为在时延m=2时的测频数据;表3为在时延m=3时的测频数据。

表1 时延m=1时的测频数据及误差值

表2 时延m=2时的测频数据及误差值

表3 时延m=3时的测频数据及误差值

表4～表6是频率为10 MHz的单频信号在不同信噪比下做了100次MentoCarlo实验得到的瞬时测频仿真数据;其中表4为基于未做平均的传统相位差分的测频数据;表5为基于4点平均的改进相位差分的测频数据;表6为基于8点平均的改进相位差分的测频数据。

表4 基于未做平均的传统相位差分的测频数据及误差值

表5 基于4点平均的改进相位差分的测频数据及误差值

表6 基于8点平均的改进相位差分的测频数据及误差值

如表1～表6所示，信道化测频和瞬时测频在高信噪比时，在信噪比＞20 dB时，都具有较好的测频性能，尤其是信道化测频的精度更高;但在低信噪比时，在信噪比＜5 dB时，两者的测频性能都会下降，尤其是瞬时测频下降尤为明显，几乎完全不能测出信号的频率。然而瞬时测频的优点是测频速度快、时间短，而信道化测频的优点是能分选不同的信号并能有较高的测频精度。