一种基于最小二乘法的RTCP自动测量循环

黄玉彤 方跃炽 刘 沛 李兴岳 李耀东 杨立波

(科德数控股份有限公司，辽宁 大连 116600)

刀具旋转中心编程功能(RTCP)是五轴机床的重要基础功能，该功能可以让用户通过调整刀具和工件的相对姿态来改善切削条件，提高加工效率，是高档数控系统的标志性功能之一。

由于数控系统实现RTCP功能时，需要计算旋转轴旋转带来的线性轴偏差从而进行补偿，因此机床的RTCP精度直接受到机床相关几何尺寸测量精度的影响。

一般情况下，机床在出厂时的RTCP相关几何参数通过手工进行标定，这就带来了测量精度准确性和稳定性的波动。同时，机床需要在一定时间内进行RTCP参数的重新校正，这对测量工作耗费的时间提出了一个比较高的要求。目前，国外数控系统多通过使用测头的自动测量循环来实现机床RTCP相关参数的自动标定，例如西门子数控系统使用CYCLE996循环来进行RTCP参数的自动标定。RTCP相关参数的自动标定功能目前已经成为高档数控系统不可或缺的重要组成部分。

GNC60系列数控系统根据最小二乘法原理开发相应的方法来提高测量循环的计算精度，有效满足了自动测量循环的需求。

1 数学原理

1.1 最小二乘法

最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知数据，并使这些求得的数据与实际数据之间误差的平方和为最小。

如果数组X和数组Y之间存在如下线性关系[1]

式中：m代表有m个等式，n代表有n个未知数β，m>n；用向量方式表示为

Xβ=Y

显然，正常情况下，超越方程无解可言，因此我们将问题转换为使方程的值最小，即实测值与计算值之间误差最小问题。

1.2 最小二乘拟合圆的实际应用

给定两组数据X=[X1,X2,…,Xm],Y=[Y1,Y2,…,Ym],假设X和Y之间的关系可以用一个圆的方程表示为如下形式：

R2=(Xi-A)2+(Yi-B)2

令a=-2A,b=-2B,c=A2+B2-R2，则可转化为标准方程形式如下：

(i=1,2,…,m)

的最小值问题。

要求得最小值，只需使方程两边同时对系数a、b、c求偏导，并令所有导数方程为0，即可求得所需方程的系数。

同理，我们也可以将此方法扩展到空间上实现三组数据的所在球体的拟合，进而得到球心坐标和半径。

1.3 空间散点拟合平面的计算

给定3组数据X=[X1,X2,…,Xm],Y=[Y1,Y2,…,Ym]，Z=[Z1,Z2,…,Zm],可计算出三组数据的平均值构造的矢量为：

我们定义矩阵D有如下形式：

利用D构造三维方阵F：

我们可以求得矩阵F的3个特征值为λ1、λ2、λ3，取最小特征值所对应的特征向量为V=[V1,V2,V3]。

假设X、Y、Z所在的平面的标准方程为

aX+bY+cZ+d=0

根据上述计算所得参数，我们可求得

a=V1

b=V2

c=V3

d=-(a×A1+b×A2+c×A3)

此时求得的a、b、c也就是平面的单位法向量。

根据最小二乘原理，可求得X、Y、Z所在空间球的球心坐标A、B、C的值，进而计算球心到平面的距离如下：

根据法向量和球心到平面的距离，我们可求得平面所在圆心的坐标为

2 RTCP参数自动测量循环

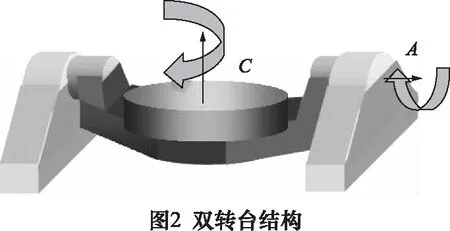
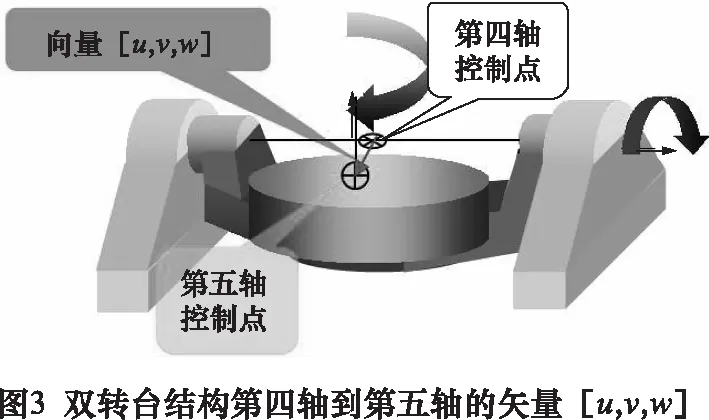
我们以双转台XYZAC结构的五轴机床(图2)为例，在机床坐标系下测量出AC的轴心坐标，可以计算得到机床坐标系下A轴轴心到C轴轴心的矢量和C轴轴心的坐标(图3)，即为需要标定的RTCP相关参数。

机床的RTCP参数自动标定方案：

首先放置标准球在转台上，放置位置为转台非圆心的任意位置。在保持C轴不动的前提条件下，转动A轴到10个不同位置如图4所示。数控系统使用测头自动测量得到标准球在相应A轴位置的10个机床坐标系下的XYZ坐标值，如表1所示。数控系统使用这10个数据点进行最小二乘法拟合计算得到圆心坐标值，作为A轴控制点的坐标值。

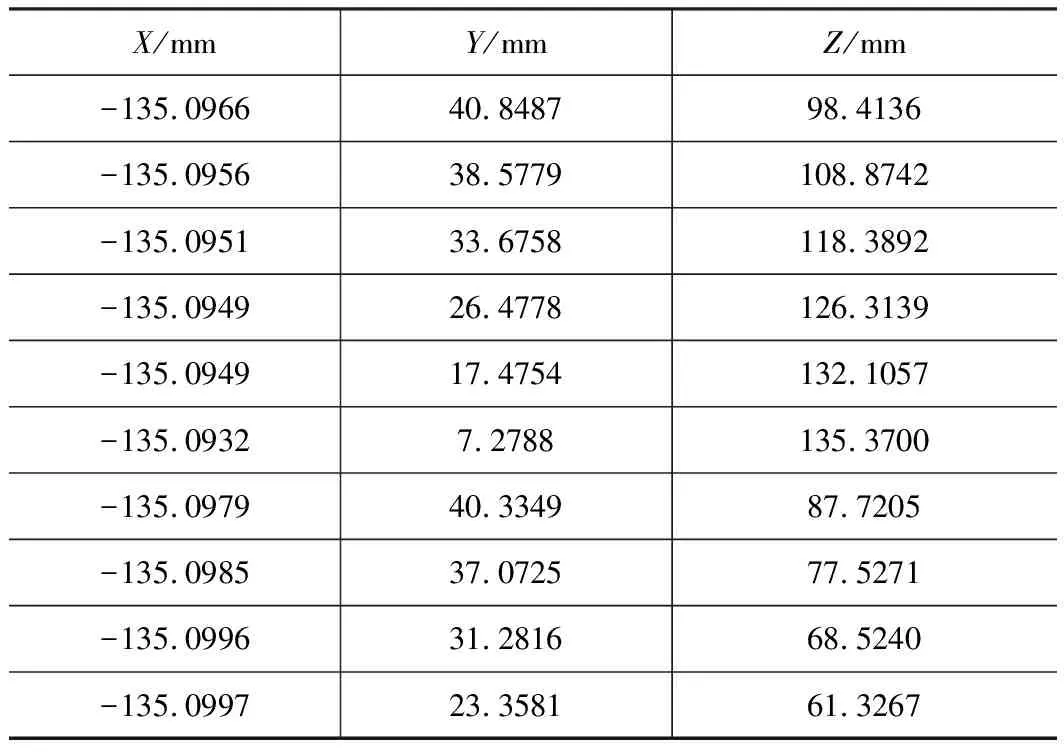
表1 转动A轴测量的数据点

然后，在A=0的状态下，转动C轴到10不同的位置，如图5所示。数控系统使用测头自动测量得到标准球在相应C轴位置的10个机床坐标系下的XYZ坐标值，如表2所示。数控系统使用这10个数据点进行最小二乘拟合计算得到圆心坐标,作为C轴控制点的坐标。

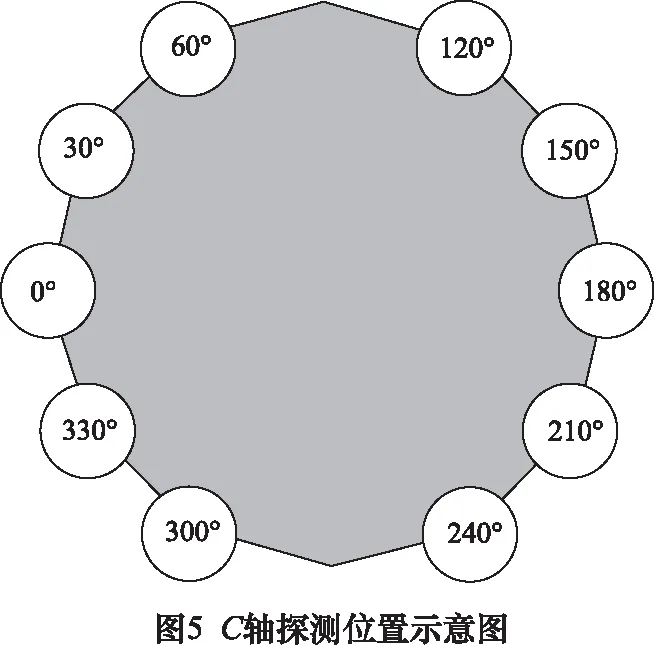
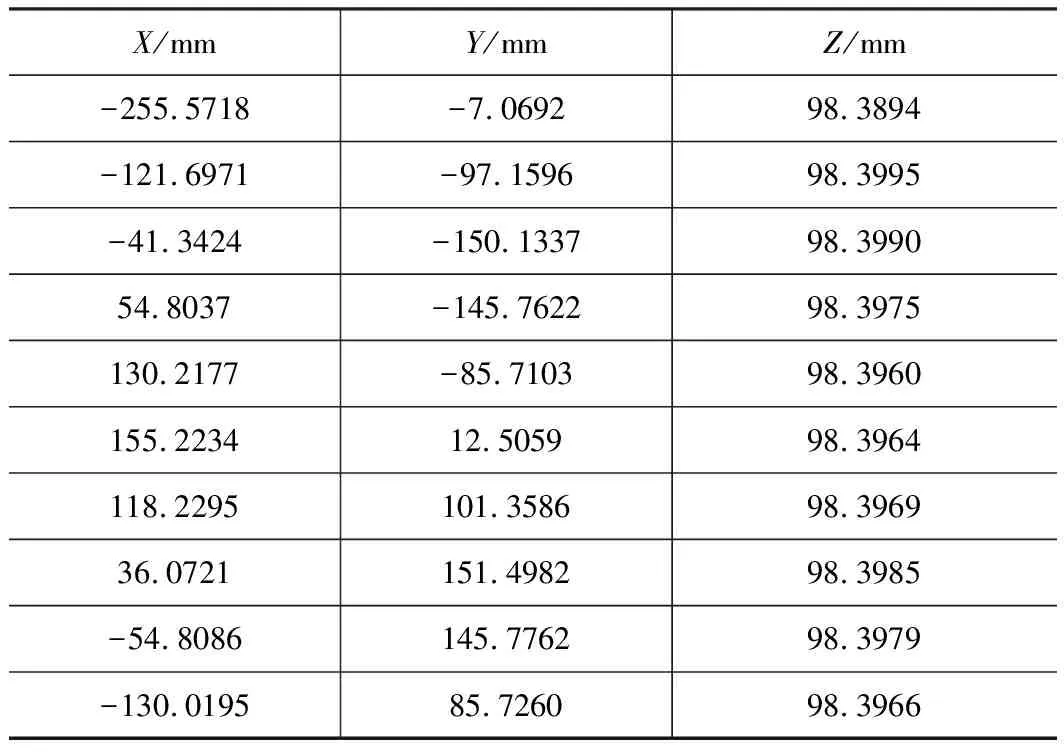
表2 转动C轴测量的数据点

3 实际机床的验证

在科德KMC600S U机床上使用自带的无线测头进行了RTCP参数自动测量循环的验证。

根据上述的RTCP参数自动标定方法，使用表1的数据可计算得到在机床坐标系下A轴的控制点坐标为[-135.096 8,-0.016 7,95.017 6]。使用表2的数据可计算得到在机床坐标系C轴控制点的坐标为[-31.430 2,-1.109 9,98.396 6]。两个点的坐标值相减可以得到A轴控制点到C轴控制点的矢量：

[U,V,W]=[-31.4302,-1.1099,98.3966]-

[-135.0968,-0.0167,95.0176]=

[103.6666,-1.0932,3.379]

矢量[U,V,W]和C轴控制点坐标[-31.430 2,-1.109 9,98.396 6]即为数控系统所需的RTCP相关几何参数。

4 结语

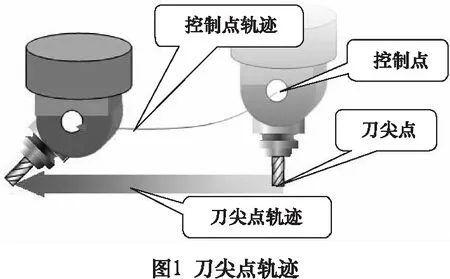
使用最小二乘法对RTCP测量数据进行拟合，可得到第四轴和第五轴控制点的坐标，进而求出RTCP所需的标定参数。可以更好更快地达到保证刀尖点按指令既定轨迹运动的目的。

通过将标准球装在主轴上，千分表架在机床台面上，开启手动RTCP功能，转动旋转轴，观察表的跳动量，作为机床RTCP动作的精度判别标准，如图7所示。

经过数据对比和机床测头测得的数据，测头补偿数据(表3和表4)准确性提高，补偿后，打表复检RTCP误差值不断减小，精度逐步提高。

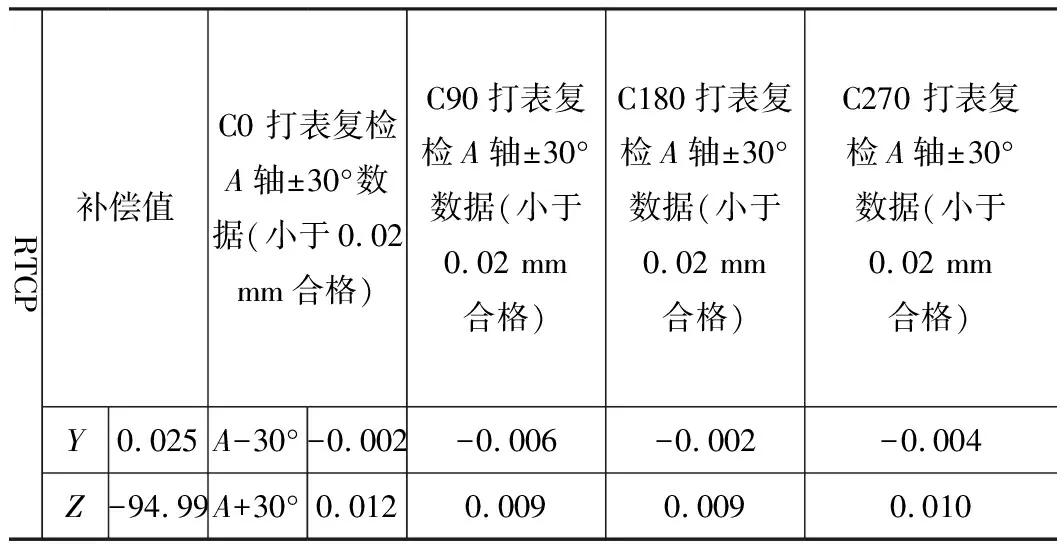
表3 原始数据

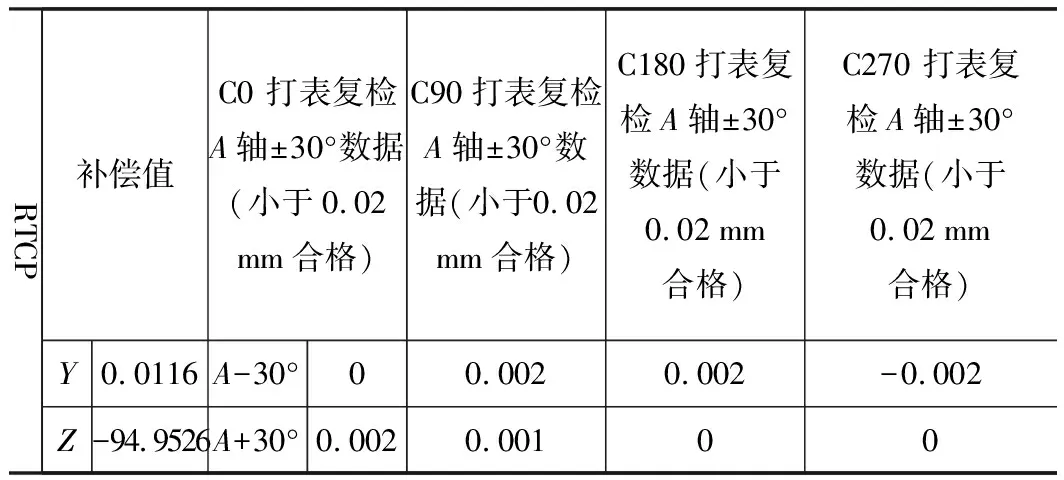
表4 补偿数据

经过打表检查机床RTCP精度后，再通过加工S形试件，反映机床的实际RTCP加工精度，如图8所示。

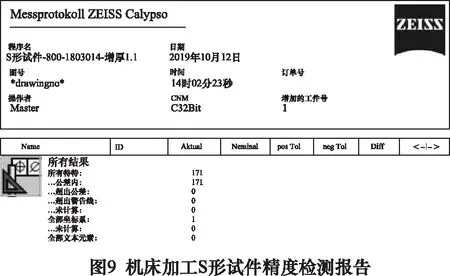
最终，通过三坐标的精度检测，满足试件加工的精度要求，报告如图9所示。

由机床的RTCP精度检测和实际S试件加工的精度检测报告证明该方法得到充分的验证，并已经在GNC60数控系统上进行应用。可以保证刀尖点轨迹的正确运动。