AccSMBO:一种基于超参梯度和元学习的SMBO加速算法
2021-01-05程大宁张汉平李士刚张云泉
程大宁 张汉平 夏 粉 李士刚 袁 良 张云泉
1(中国科学院大学 北京 100190)
2(中国科学院计算技术研究所 北京 100190)
3(智铀科技有限公司 北京 100190)
4(苏黎世理工大学 瑞士苏黎世8914)
5(纽约州立大学布法罗分校 纽约 14260)
随着机器学习技术的发展,自动机器学习技术成为了机器学习的关键技术之一[1],即AutoML技术.当前的机器学习模型的训练需要大量的超参,超参优化是AutoML的重要部分.
为了解决上述问题,超参优化成为了一个非常热门的研究方向.近年来研究者提出了不同的超参优化方法,如Hyperband算法SMAC算法、TPE算法等.这些算法将历史调参信息或者梯度信息作为输入,使用不同模型对最优超参进行预测,从而迭代求解出最优超参.
基于超参梯度的调优是超参调优的重要手段之一,现有的很多工作已经形式化定义了超参梯度并开发出了相关的调参算法.除了超参梯度,元学习也是现代超参调优的重要研究方向.传统元学习方法依照任务目标.机器学习模型和数据集的不同对最优调参任务进行分类,并记录其最优超参值.每次遇到新的机器学习任务时,都从原有的记录中寻找历史记录中这类情况的最优超参.此外,基于经验的人工调参是现有主流调参手段.相比于调参算法,人工调参可以在机器学习训练中的不同阶段灵活依照经验调参.
序列模型优化算法(sequential model-based opti-mization algorithms, SMBO)是现在最好的超参优化算法框架[2]之一.然而,作为黑箱优化算法的延伸,传统的SMBO算法不考虑已有的超参信息.非常显然的是,合理使用已知的超参信息可以加快黑箱调优算法的收敛速度,提升搜索到的超参的效果.
我们总结出机器学习使用的超参常常满足2个超参规律,这2个规律往往是在超参调优前可以得到的已知的超参信息:1)超参-效果之间的关系往往是充满“噪音”的单峰或者单调的函数.这种趋势上简单的函数意味着使用传统SMBO算法求解超参优化问题时,往往使用较少的采样点即可拟合出总体趋势.但是超参-效果之间的关系在局部上往往充满了“噪音”,这意味着过分依赖局部信息,如梯度,过分依赖局部信息会导致拟合函数对总体趋势的表述变形.2)最优超参的分布情况往往是不均匀的,即有些超参容易取特定的几个值.
基于上述相关的技术和我们总结的规律,针对SMBO算法,我们考虑2个问题:1)如何使用超参梯度加速调参速度,其中的难点是合理使用超参梯度信息的同时避免局部“噪音”带来的影响;2)如何使用元学习,替代人工调参中经验的成分进而加速调参.
本文提出了AccSBMO算法.AccSMBO使用3种方法来优化传统SMBO算法.
1) 基于第1个超参规律,我们设计了基于梯度的多核高斯过程回归模型来拟合观测值和观测梯度值.基于此,AccSMBO可以更快地建立完整有效的超参-效果模型(也称作响应面[3]).基于梯度的多核高斯过程回归模型具有良好的抗噪能力和较少的计算负载.
2) 基于第2个超参规律,AccSMBO使用meta-acquisition函数替代原本的获取函数.基于元学习数据集,AccSMBO寻找出现最佳超参概率较高的范围(称为最佳超参高概率范围),并使用EPDF(empirical probability density function)表述这一范围.在每次AccSMBO迭代中,AccSMBO算法基于EPDF提供的信息,在最佳超参高概率范围内选择预测最优值.
3) 同样基于第2个超参规律,我们在并行方法上设计的策略:在SMBO自然对应的并行算法中,为了充分使用并行资源,将更多并行计算资源用于探索最佳超参高概率范围,AccSMBO算法使用了基于元学习数据集的并行资源调配方案.这使得在计算超参效果的过程中充分利用计算资源,减少计算过程中同步操作的消耗,同时将计算资源倾斜在最佳超参高概率范围中.
上述3种方法加快了SMBO的收敛速度:在实验中,在不同数据集上,从迭代次数上,串行AccSMBO算法的收敛速度是SMAC算法速度的175%~330%,是HOAG算法的100%~150%;从绝对时间上,串行AccSMBO算法的收敛速度是SMAC算法的167%~329%,是HOAG算法的109%~150%.从绝对时间上,使用4个worker的并行AccSMBO算法的收敛速度是SMAC算法的322%~350%,是HOAG算法的145%~316%.从调优结果上,AccSMBO算法和SMAC算法在所有数据集上都找到了最优效果超参,HOAG算法在小规模数据集上未能收敛.
1 相关工作
近年来,自动机器学习工具相继被开发出来,如谷歌的AutoML,Auto-Weka,AutoSklearn等[4].这些工具使用了不同的超参优化算法.
在上述的应用中,研究人员通常在所有参数空间使用网格搜索,但随着超参数量的增加,这种搜索很快变得令人望而却步.
贝叶斯优化算法[2-5]是最常用的用于超参数调优的黑箱优化算法.贝叶斯优化算法通过假设损失函数的先验分布,然后根据新的观测值不断更新该先验分布.每一个新的观测值都是根据一个获取函数计算得来,这个函数负责维持整个探索过程的开发和探索平衡(exploitation and exploration trade off),使得新的观测值能带来更好的结果,或者有助于获得更多关于超参-效果函数的信息.
随机优化方法是现在最常用的超参调优方法,例如网格搜索、随机搜索、启发式算法和神经网络算法[6],但是这类算法效率低下.
傅里叶分析法是近几年发力的超参调优算法,如Harmonica[7]算法.傅里叶分析法也叫作低阶布尔函数多项式拟合法,这类方法首先随机选取抽样点,再使用正交函数组拟合这些采样点[8-10],进而使用拟合函数预测最优超参值.
决策理论方法考虑的是在现有超参候选集中使用最少的资源选出最佳超参,这类算法在机器学习模型的训练中逐步寻找该模型可能的效果下限,早停效果不好的机器学习模型的训练[11].这种算法最常见的是Hyperband算法[12].
在用于超参调优的贝叶斯优化算法[2,4,13]中,SMBO算法[2]框架使用最为广泛.SMAC[2](sequential model-based algorithm configuration),TPE[14](tree-structured parzen estimator)和基于高斯过程的SMBO算法[15]是当前效果最好、求解速度最快的SMBO算法实现.
随着计算平台的发展,并行计算环境逐渐成为了机器学习计算环境的主流.并行贝叶斯调优算法也逐渐成为了研究热点[16-19].
如何使用元学习(metalearning)[20]和超参梯度[21-23]加速自动调参优化过程是AutoML领域中讨论最多的话题之一.
2 研究背景
2.1 问题定义
本文使用形式化定义超参优化[4]问题:
给定一个由参数λ所影响的学习算法A(λ),和数量有限的数据集D={(x1,y1),(x2,y2),…,(xm,ym)},超参优化是寻找最优超参λ使超参-效果函数f取到最小值的任务.f需要由算法A(λ)和由数据集D产生的训练集Dtrain、验证集Dvail来计算得出.对超参优化问题的表述可表达为

(1)
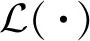
2.2 算法背景
2.2.1 SMBO算法及其最优实现
SMBO算法是用于超参调优的黑盒优化算法框架.

算法1.SMBO算法.
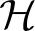
Repeat
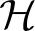

④λ←从③中的超参集中选出最优超参;
⑤ 计算f(λ);
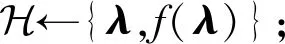
Until消耗完给定计算资源;
许多研究者提出了不同的算法来填充SMBO算法框架.表1总结了现有效果较好的算法实现.

Table 1 State of the Art Algorithm for SMBO Algorithm Frame表1 SMBO算法中不同步骤可选择的算法
元学习是提升SMBO算法效果的重要手段.基于元学习方法,SMBO可以在第1轮迭代到第2轮迭代中取到最优或者次最优的超参值.但是,为了通过元学习取得较好的超参初始值,经常需要花费较多成本构建足够大的元学习数据库.
为了较好地反映出原函数f(λ)的趋势,不同研究提出了不同的响应面模型,但是这些模型并没有考虑如何合理使用梯度信息.在这些模型中,最常使用且效果最好的响应面模型是随机森林和高斯过程[13].使用随机森林和高斯过程的SMBO算法实现的是SMAC算法.因此本文实验的主要benchmark是SMAC算法.
现有效果最好的AC函数是EI(expected improvement)函数[3],EI函数使用期望下降值作为输出,EI函数是最为常用的AC函数的选择.因为我们的加速方法并没有涉及AC函数的选择,所以在实验中使用EI函数作为AC函数.
算法1的第④步的主要目的是从有限个超参中使用最少的资源选择出效果最好的超参.这一步中最好的算法是Hyperband算法和intensify process.因为加速算法不涉及如何在这一步选择最优超参,因此在实验中,AccSMBO算法在这一步使用intensify process算法.
2.2.2 代
在SMBO算法中,本文称一轮循环为一代(epoch).在每一代中,SMBO算法都需要做相同的工作:构建模型—选择超参—计算超参效果—写入历史,从而SMBO算法在每一代花费的时间基本相同,因此SMBO算法中的一代是测量SMBO算法性能的最小单位.
在本文的实验中,除了以时间作为衡量指标的实验外,还会增加以代作为实验衡量指标的实验,基于2点原因:
1) 因为算法在代码实现和运行平台上的不同,每代所花费的时间在不同情况下也不尽相同,而当初始值和参数设置几乎一致时,调优过程几乎是稳定的,所以在读者复现本实验时,横坐标为代的实验结果可以用较少代价得到复现.
2) 更重要的是,绝大多数算法,如d_KG算法[23]和Hyperband算法[12]的理论结果、理论分析所用的指标均为迭代次数,即代数.所以使用代作为横坐标可以更好地对应理论结果.
高斯过程是现有最好的响应面的选择之一[27].基于高斯过程的SMBO算法是最常用的SMBO算法实现之一[15].
本文中,设置λ包含了d个不同的超参.k(·,·)是内核函数(协方差函数).
本文中定义向量
f=(f(λ1),f(λ2),…,f(λn))T,
其中,f维度为n.
定义矩阵Mλ=(λ1,λ2,…,λn)T,其维度是d×n.
定义维度为n×n的内核矩阵K(Mλ,Mλ):
定义K(λ*,Mλ)形式为
K(λ*,Mλ)=(k(λ*,λ1),k(λ*,λ2),…,k(λ*,λn)).
m(λ*)=γK(λ*,Mλ),
γ=K(Mλ,Mλ)-1f.
协方差函数形式为
var(λ*)=k(λ*,λ*)-
K(Mλ,λ*)K(Mλ,Mλ)-1K(Mλ,λ*).
2.2.4 超参梯度
很多工作都提供了基于超参梯度的优化方法[21,22].超参的梯度可以定义和计算[22]:

现有很多基于超参梯度的优化方法都是基于梯度下降.
2.2.5 元学习数据库
元学习(metalearning)是加速SMBO算法的重要手段.依照分类或者回归任务的不同,数据集特征的不同和目标函数的不同,元学习可以提供针对不同情况的最优或者次优的参考超参.元学习数据集记录了在不同情况下的这些最优超参.SMBO算法可以将元学习提供的参考超参作为初始值,进一步搜索得到更好的超参,从而加快超参搜索速度.
尽管元学习在AutoML中取得了巨大的成功,对于大多数情况,元学习只有在元学习数据集庞大的基础上才能取得足够好的效果.当元学习数据集较小时,元学习对AutoML的提升有限.
2.2.6 并行SMBO算法
作为贝叶斯优化算法的一种,SMBO算法也可以先天在并行环境中得到加速.现在最优的贝叶斯优化算法是2018年提出的异步并行贝叶斯优化算法[16].这种优化算法使用异步并行的方法避免了集群间同步的开销,在工程上受益.这种异步并行的SMBO算法是可以实现在当前主流机器学习框架-参数服务器上的.异步并行的SMBO算法在算法2中给出.
算法2.异步并行SMBO算法.
Worker端:
Repeat
① 计算从server接收预测最佳超参λ;
② 计算λ对应的f(λ);
③ 将(λ,f(λ))推回server;
Until计算资源耗尽.
Server端:
① 将λ1,λ2,…,λk给worker1,worker2,…,workerk,使得worker1,worker2,…,workerk开始计算f(λ1),f(λ2),…,f(λk);
Repeat
② 从workeri中接受一个(λpre,f(λpre))组;
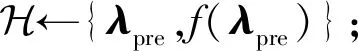
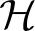

⑥λnext←从⑤中的超参集中选最优超参;
⑦ 将λnext发给workeri计算f(λnext);
Until计算资源耗尽;
3 出发点和主要思想
对于大多数超参,超参—性能函数f(λ)经常呈现2种模式:1)f(λ)的全局变化趋势简单,f(λ)在全局上经常呈现为单调函数或单峰函数.但是,超参的效果局部变化趋势是不稳定的,即充满了噪音,如图1所示.图1中展示了在决策树和GBDT模型中不同超参对模型效果(log loss)的f(λ).图1具体呈现了模式1).2)最佳超参的分布不是均匀分布.实际调参时,调参人员经常会提前知道一些先验的、合理的范围,即最佳超参高概率存在的范围.很明显,元学习数据集可以反映这些信息.通过总结Auto-Sklearn中元学习模块使用的数据集,图2展示了在F1范式多分类任务中一些参数的频度统计情况与其拟合的概率密度分布函数.图2展示了最佳超参分布不均的特点,同时展示了如何通过函数拟合统计值得到EPDF函数.
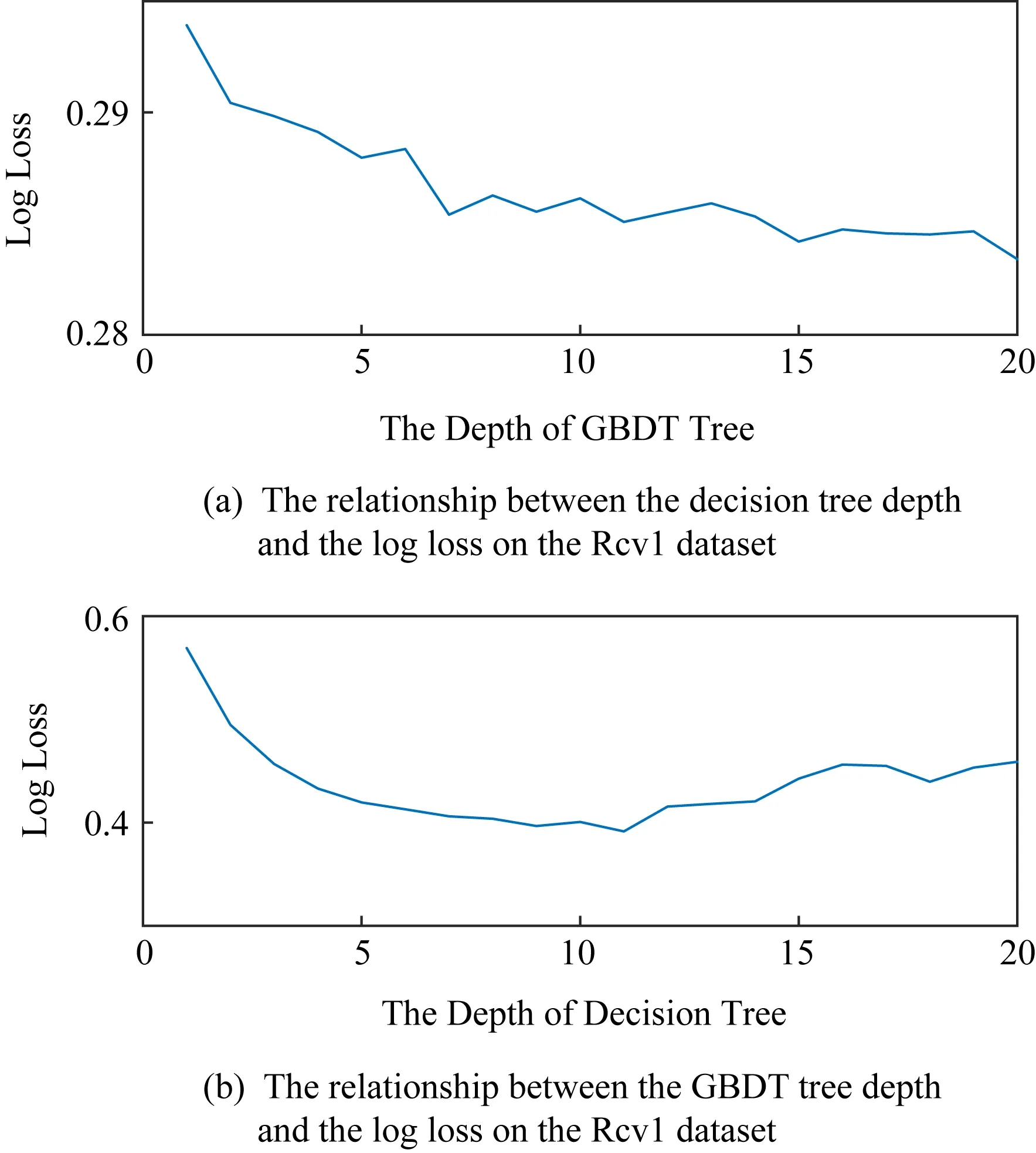
Fig. 1 Some of those performance functions are close to unimodal functions or monotonic functions图1 f(λ)曲线在全局上经常呈现为单峰函数或者单调函数
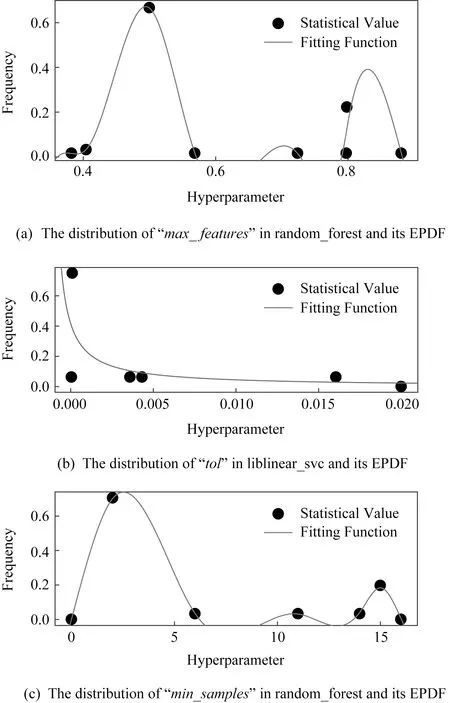
Fig. 2 The frequency and its EPDF of hyperparameter value for F1 norm multi-class task on sparse dataset图2 稀疏数据集下F1范式多分类任务中超参分布情况及其EPDF
为了在SMBO算法中充分利用模式1)、模式2),我们提出了AccSMBO算法,串行AccSMBO在算法3中给出.异步并行AccSMBO算法在算法4中给出.
AccSMBO使用了2种方法提升了传统串行SMBO算法的效果和一种资源调度方法提升并行SMBO算法的效果.1)AccSMBO使用了基于梯度的多核高斯过程,AccSMBO使用的高斯过程可以最大程度上利用梯度信息,同时可以避免精细拟合梯度信息而导致噪音对拟合过程的负面作用;2)在迭代过程中,AccSMBO使用元学习数据集调整AC函数,即metaAC函数(meta-acquisition functions).metaAC函数可以在最佳超参高概率范围中有较高输出,使得AccSMBO算法将更多的搜索资源放在最佳超参高概率范围中,加快搜索到最佳超参的效率;3)根据元学习数据集,我们优化了并行AccSMBO算法.使在最佳超参高概率范围中的超参使用更多的计算资源,加快搜索到最佳超参的效率.
算法3.串行AccSMBO算法.
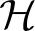
Repeat
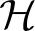
③ 使用元学习数据集和AC函数计算metaAC函数;

⑤λ←从④中的超参集中选出最优超参;
⑥ 计算f(λ);

Until消耗完给定计算资源;
算法4.异步并行AccSMBO算法.
Worker端:
Repeat
① 计算从对应的栈中接收弹出的预测最佳超参λ;
② 计算λ对应的f(λ);
③ 将(λ,f(λ))推回server;
Until计算资源耗尽.
Server端:
① 将λ1,λ2,…,λk+m给workerk+1,workerk+2,…,workerk+m,使得worker1,worker2,…,workerk+m开始计算f(λ1),f(λ2),…,f(λk+m);
Repeat
② 从workeri中接受一个(λpre,f(λpre))组;
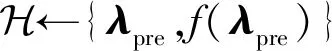
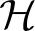
⑤ 使用元学习数据集和AC函数计算metaAC函数;

⑦λnext1,λnext2,…,λnextq←从⑤中的超参集中选q(q>2)个最优超参;
⑧ 分别判断λnexti的优先级并压入stackfast或者stackslow中;
Until计算资源耗尽;
4 AccSMBO算法
4.1 基于梯度的多核高斯过程
4.1.1 数学符号
本节主要介绍后文中使用的额外的数学符号.
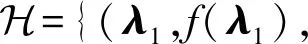






本文中,将矩阵的组合简写为
Km:n=(Km;Km+1;…;Kn).
4.1.2 基于梯度的多核高斯过程回归
本文设计了一种新的基于梯度的高斯过程回归方法,这种算法在算法5中给出.
算法5.基于多核高斯过程回归算法.

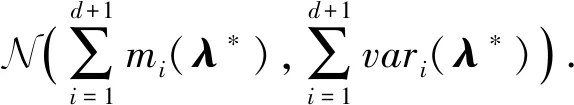
① 使用最小二乘法求解式(5)中的α和β:

(2)
②m(λ*)=K2:n(λ*,Mλ)α+K1(λ*,Mλ)β;
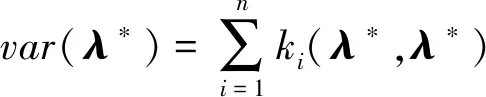
4.1.3 均值函数
在传统的高斯过程回归中,均值函数m(λ)是使用内核函数作为基底对观测点的拟合函数.

f=K1(Mλ,Mλ)α1+K2(Mλ,Mλ)α2+…+
Kd+1(Mλ,Mλ)αd+1,
(3)

(4)
通过式(3)、(4)可解得α1,α2,…,αd+1,则
4.1.4 方差函数
多核高斯过程的方差反映了预测点λ*与观测点λi之间的距离.对于使用ki(·,·)作为内核的高斯过程,其方差函数的计算方法为vari(λ*)=ki(λ*,λ*)-Ki(Mλ,λ*)Ki(Mλ,Mλ)-1Ki(Mλ,λ*).因为高斯过程的和依旧为高斯过程,和的高斯过程的方差是不同高斯过程方差的和,所以多核高斯过程回归的数学形式为
4.1.5 抗噪、约近和计算负载的减少
虽然径向基核函数(radial basis function, RBF)满足了拟合梯度的要求:提供了足够多线性无关的内核函数,但计算负载的减少和抗噪能力的增加也是考量的重点之一.正如第3节中提到的,从整体上,f(λ)相对简单,但曲线的局部充满了噪音.梯度反映的是曲线的局部信息,而不是f(λ)曲线的总体趋势.对梯度信息的精确拟合会对高斯过程回归产生负面影响,并且增加计算量:如当历史超参的梯度因为噪音与总趋势相反时,梯度信息的精确引入会对高斯过程回归产生非常显著的负面影响,如图3所示.
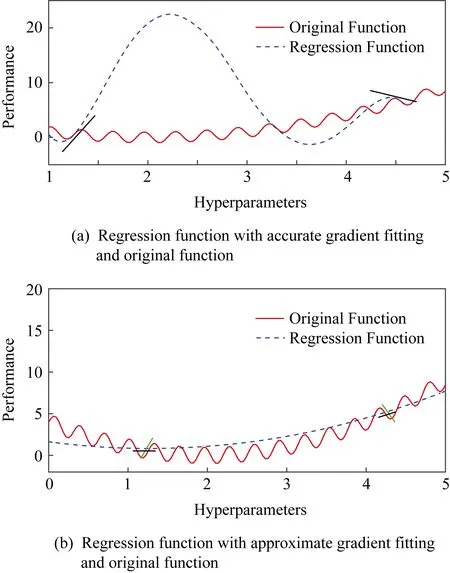
Fig. 3 Regression function with different accurate gradient and original function图3 使用不同精准度的梯度的拟合函数与原函数
AccSMBO算法可以通过减少核函数的数量来减少梯度噪音带来的影响.在实践中,噪音越多,使用的内核数量就越少.在求解方程时,式(3)(4)的地位是不同的.在大多数情况下,噪音对梯度方程的影响会更大,如图3所示.因此,我们期望α和β可以满足式(3),然后使用最小二乘法来求解式(4)除此之外,减少内核可以减少计算的负载.
因此,考虑到f(λ)曲线的性质和计算负载,上述基于梯度的多核高斯过程回归更适合于解决超参优化的问题.
4.2 metaAC函数
现有SMBO算法都是在使用者对目标函数毫无所知的情况下设计的.但是在真实情况下,算法使用者对超参都有一些了解.元学习数据集可以反映出这些信息.合理使用这些信息可以提升超参调优的速度.基于这些信息,本文提出了metaAC函数对SMBO算法进行加速.
4.2.1 metaAC函数及其收敛性
使用metaAC函数需要2个步骤:1)为了使得metaAC函数在最佳超参高概率范围的输出较高,需要根据元学习数据集总结出最佳超参高概率范围.2)依照最佳超参高概率范围,在保证收敛性的前提下调整AC函数.
最佳超参的概率密度分布函数是最佳超参高概率范围的表达方式之一.AccSMBO算法使用最佳超参的概率密度分布函数对AC函数进行调整.AccSMBO根据元学习数据集中的信息构建一个经验概率密度分布函数:首先,根据元学习数据集中的信息统计出不同超参的频率;然后,使用函数依照频率分布的信息拟合得到概率密度分布函数p(λ)(简写为EPDF).
构建最佳超参的概率密度分布函数并不要求元学习数据集包含不同情况下所有的最优超参值,只需要元学习数据集能够反映出最优超参分布的趋势即可.此时p(λ)就可以表达出最佳超参高概率范围信息.p(λ)的输出区域越高,则这一超参越有可能成为最优超参.
在设计metaAC函数时,metaAC应具有2个性质:1)在迭代优化的过程中,p(λ)输出高的区域应具有更高的优先权,这样有更大概率更快地找到最优超参.2)随着算法的进行,p(λ)的影响应该递减.过度依赖p(λ)会严重破坏AC函数的开发和探索平衡(exploitation and exploration trade off),从而导致随着迭代地进行AccSMBO算法无法描绘出目标函数的全局形式.
基于上述的性质,本文设计了metaAC函数:
metaAC(λ,epoch,p(λ),AC(λ))=
AC(λ)×(rate×p(λ)×e-epoch+1-rate×e-epoch),
其中,rate∈[0,1].rate主要用于描述元学习数据集是否足够完整和算法使用者想多大程度依赖于元学习数据集进行加速.元学习数据集越大越完整时,rate应越大.
metaAC函数实际上是传统AC函数的调整,而且可以看到随着迭代地进行,metaAC函数将会收敛于传统的AC函数.换句话说当在资源充足的情况下,metaAC函数的收敛性证明等同于未被调整过的AC函数的证明,即metaAC是可以保证算法收敛的.
在实际的生产中,遇到的最优超参在最优超参高概率范围内的情况更多一些.从图4(a)和图4(b)中可以看到,metaAC函数比起AC函数更侧重于搜索最优超参高概率范围,从而起到加速算法的效果.

Fig. 4 The change of AC function to metaAC function图4 从AC函数调整到metaAC函数
4.2.2 元学习的缺陷和metaAC的优势
元学习是当前提升超参调优的重要手段.但是元学习技术存在2个问题:1)当前元学习技术只能给超参调优提供最优/次优的初始值.元学习技术不能在调参过程中对调优算法产生影响.2)元学习数据集一定要非常大.如果元学习数据集较小,对于元学习数据集中没有被记录的任务,元学习就难以提供较好的参考超参.同时,因为AC函数会进行开发探索平衡,在提供较好的初始值之后,AC函数会选择在未探索区域中进行探索,而往往未探索的区域存在最优超参的可能性比较低,如图4(a)所示,对于没有被采样过的区域[3,6],因为没有被探索过,AC函数的输出更高.
metaAC函数可以克服上述的2个缺点:1)metaAC函数参与到了自动调优的过程中;2)metaAC函数的构造并不需要非常完整的元学习数据集.metaAC函数只需要元学习数据集反映出整体的趋势即可.
4.3 异步并行AccSMBO算法
并行算法的高效优化一直是并行计算领域关注的重要问题.传统对贝叶斯优化算法的并行加速是一个成熟的领域.但是基于第3节中固有模式和元学习数据集,可以进一步加速异步并行AccSMBO算法.
因为最佳超参在最佳超参高概率范围中出现的概率较高,因此,将更多资源投入到最佳超参高概率范围中,基于EPDF提供的最佳超参高概率范围,异步并行AccSMBO算法可以将更多资源用于探索最佳超参高概率范围中的参数,将f(λ)在最佳超参高概率性范围中的情况尽快描绘出来.
AccSMBO使用了图5所示的算法.在设计并行资源调度算法时,AccSMBO设置2个栈stackfast和stackslow.新产生的预测点包含了更多关于f(λ)的信息.因此总是优先计算最新更新的预测点,即使用栈数据结构.每次worker计算λ时,都从对应的栈中弹出的最新的λ用于计算效果.不同的worker使用异步并行的方法进行并行计算.异步并行极大地减少了同步操作带来的巨大计算开销,是现在最好的并行模式之一.

Fig. 5 The parallel workflow of AccSMBO图5 AccSMBO的并行工作模式
为了并行加速SMBO,AccSMBO将更多的计算资源放在最佳超参高概率范围中的预测超参,即将最佳超参高概率范围中的预测超参放在高优先级队列中.但是考虑到算法收敛性,即保证开发和探索平衡(exploitation and exploration trade off),这种资源分配的不平衡应该随着迭代的进行而逐渐减弱.基于此,使用和metaAC函数同样的设计思路,AccSMBO使用Value函数完成上述目的.
首先AccSMBO需要依照传统挑选参数的算法对候选参数集中超参的挑选顺序付给初始优先级,如intensify process或者Hyperband算法.其中优先级越高,输出越大.
例如,λ1,λ2,…,λk按照1,2,…,k的顺序被Hyperband选出,则pri(λi)=i,pri(λ)越高,优先级越高.即:
pri(λ)=选择算法选出λ的顺序.
基于pri(λ),这里使用metaAC函数的设计思路设计Value函数:
Value(λ,epoch,p(λ),pri(λ))=
pri(λ)×(rate×p(λ)×e-epoch+1-rate×e-epoch).
基于Value函数进行降序排序之后得到的序列作为候选超参的优先级.选取10%的低优先级超参进入stackslow栈,其余超参放入stackfast栈中.
异步并行AccSMBO算法的优化本质是对传统异步并行SMBO算法的调整.随着算法的逐步进行,算法5中的算法会退化为传统异步并行贝叶斯优化算法,即能保证算法收敛.
与metaAC函数的加速原理一样,实际问题中,调参人员遇到的最优超参在最优超参高概率范围内的情况更多一些.AccSMBO侧重于搜索最优超参高概率范围,从而起到加速算法的效果.
5 实 验
在本文中,实验使用HOAG算法的实验框架[22]进行实验.
5.1 问题设置
5.1.1 数据集
首先,本实验选择不同规模的数据集进行训练,包含了小规模数据集(OpenML数据库中的Pc4数据集[29])、中型规模数据集(LibSVM数据库中的Rcv1数据集[30])、大规模数据(LivSVM数据库中的Real-sim数据集[22])进行实验.这些数据集的具体情况在表2中给出.
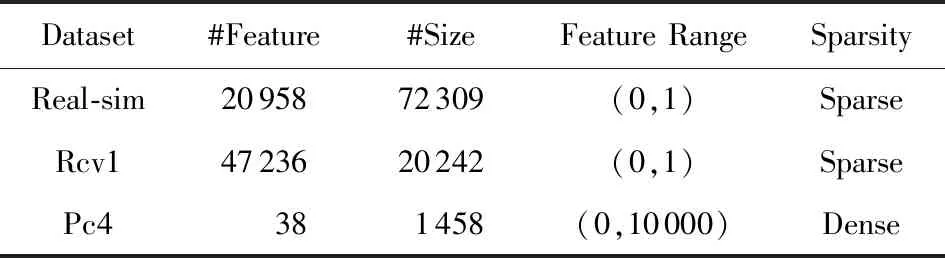
Table 2 Dataset Information表2 数据集信息
在实验中,本实验抽取30%的数据作为验证集,剩下的数据作为训练集.
5.1.2 目标问题
在实验中使用超参调优算法搜索逻辑回归模型中2阶正则参数.本实验选择这个参数作为实验参数是因为这个参数较容易求其超参梯度[21].在这个实验中,外层优化的目标为log loss,这里选择log loss是因为log loss克服了传统0-1损失带来的非凸问题和不连续问题[21].内层优化目标h(λ)是2阶正则化的logistic损失函数.目标函数的形式化表达为
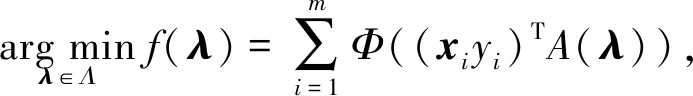
(5)
其中,Φ(t)=ln(1+e-t).在求解内层优化问题时,本实验使用了一种拟牛顿法:L-BFGS(limited-memory BFGS)算法,作为优化算法[31].其中L-BFGS算法代码经过了工业级代码优化,使用在相关广告CTR预测产品中.
5.1.3 内核函数
在实验中,超参的维度是1;因此本实验选择2个内核:高斯径向基函数和3阶径向基函数,即:
和
在本实验中,需要对矩阵K2求逆矩阵,基于对精准度的考虑,本实验选择高斯径向基函数对应的矩阵进行求逆矩阵操作.
5.1.4 元学习数据集
现有唯一开源的元学习数据集是AutoSklearn中的元学习数据集.此元学习数据集由OpenML数据集库构建.为了使实验更有说服力,实验中随机删除了这个数据集中20%的内容,并将这份数据集命名为半元学习数据集.半元学习数据集不能用于提供最佳参考超参.但是,因为半元学习数据集保留了整体超参分布的趋势,所以,半元数据集仍然可以用于构建metaAC函数.
5.1.5 算 法
本实验比较了5种现有的超参优化方法.为了使收敛过程更清晰,所有算法在选择初始值时关闭了元学习功能,并将初始值都置为1.
1) SMAC算法.SMAC算法是现有最好的SMBO算法实现之一.SMAC算法被使用在了AutoSklearn和Auto-Weka等自动调优工具中.在每一步中,AC函数选出4个超参作为备选超参.再使用intensify process从4个超参中选择效果最好的超参.本实验选择EI函数作为AC函数.
2) AccSMBO算法.AccSMBO算法代码是使用AutoSklearn代码修改而来.在实验中,设置rate=1.为了使得p(λ)更准确,本实验中,AccSMBO算法先将任务按照目标函数(log loss)、任务(二分类)和数据集特性(稀疏稠密)分类,统计分类后超参的分布情况.与SMAC算法一样,每代AC函数选择4个超参作为备选超参.在使用intensify process从4个超参中选择效果最好的超参.本实验选择EI函数作为AC函数.
3) 网格搜索.网格搜索是现在最常用的超参搜索方法之一.在实验中,网格搜索算法从区间[0,1]中均匀取出20个超参,每一轮从1开始,逐个计算一个超参的效果.
4) 随机搜索.随机搜索是现在最常用的超参搜索方法之一.在实验中,随机搜索算法从区间[0,1]中随机取出20个超参,每一轮计算一个超参的效果.
5) HOAG(hyperparameter optimization with approximate gradient)算法.HOAG算法是现在最优的使用梯度求解最优超参的算法.每一代,超参都会朝着梯度下降的方向进行调整.本实验直接使用开源的HOAG算法代码作为实验代码.在实验过程中为了保证算法收敛,实验设置εk=10-12.为了保证算法的收敛速度并且保证算法能够收敛到最小值,本实验预先采样了f(λ)曲线中的点,基于采样点的梯度估测在实验中步长最大为10-3.
6) 并行AccSMBO算法PaccSMBO.多线程AccSMBO算法.在实验中,并行AccSMBO算法使用4个worker组成的系统.在算法设置上,多线程AccSMBO算法与串行AccSMBO算法一致.在并行设置上,3个worker分配给stackfast,1个worker分配给stackslow.为了使不同worker具有不同的初始值,不同worker从[0,1]间网格地抽取使用初始值,即初始值为0.25,0.5,0.75,1.实验中,这种算法被称为PaccSMBO.
上面的5个算法分别代表了常用的搜索算法(随机搜索、网格搜索),基于梯度的算法(HOAG算法)和其他SMBO算法实现(SMAC算法).
5.2 实验环境和实验信息
本实验的实验服务器硬件环为:
服务器使用2核Intel®Xeon®CPU E5-2680 2.88 GHz,共有24个内核.同时服务器使用最大内存为60 GB.
服务器使用网卡为Intel Corporation I350 Gigabit Network Connection.
本实验的实验服务器软件环境为:
操作系统为CentOS 7.5.1804系统,C/C++编译器版本为gcc 7.3.
Python版本为Python 3.7.5,SMAC的版本为SMAC-0.8.0,参数服务器使用MXNet(版本为1.1.0)中的参数服务器模块.
5.3 实验结果和分析
在串行算法的比较中,从代数上看,串行Acc-SMBO算法的收敛速度最快,同时搜索到了最好的超参,而SMAC找到了次优的超参.串行AccSMBO算法的收敛速度是SMAC的330%.由于当数据集规模较小时,f(λ)曲线不稳定,f(λ)曲线的梯度信息充满了噪音,不能够指示曲线的走向.因此会导致HOAG算法的收敛速度减慢.在本实验中,HOAG并没有达到收敛.对于并行的AccSMBO算法(PaccSMBO算法),尽管从代数上PaccSMBO算法没有占有优势,但因为是4个worker同时运行,所以绝对时间上少于串行AccSMBO算法:串行AccSMBO算法使用3代达到收敛,PaccSMBO算法使用9代达到收敛,平均每个worker运行时间为2代.从绝对时间上看,串行AccSMBO的收敛速度是SMAC的329%,由于通信的损耗,并行Acc-SMBO算法(PaccSMBO算法)几乎同时与串行AccSMBO算法收敛.

Fig. 6 Algorithm iteration performances on thedifferent datasets图6 不同算法在不同数据集上的迭代性能
在Pc4实验中,由于HOAG算法使用精确的梯度作为优化方向,在这种情况下无法找到最佳的超参.黑箱优化算法在这里显示了它的优势,因为它减少了曲线中的“噪声”的影响,更快地逼近梯度.图6(b)和图7(b)显示了Rcv1数据集的实验结果.同样地,在串行算法的比较中,从代数上看,串行AccSMBO算法的收敛速度最快,并找到了最佳的超参.在Rcv1数据集中,f(λ)曲线特性相对稳定,接近单峰函数,所以HOAG算法找到的超参和收敛速度是次优的.AccSMBO算法的收敛速度是HOAG算法的150%,是SMAC算法的收敛速度的175%.SMAC算法得到的结果和收敛速度几乎与随机搜索相同,因为SMAC需要更多的采样点来构建整个f(λ)的信息.并行AccSMBO算法(PaccSMBO算法)的收敛过程虽然在绝对的代数上比串行AccSMBO算法多,但是平均到每个worker,其消耗的代数会比串行AccSMBO更少,绝对时间会更快.从绝对时间上看,串行AccSMBO算法是HOAG收敛速度的150%,是SMAC算法的167%.PaccSMBO算法的收敛速度是HOAG算法的316%,是SMAC算法的350%.
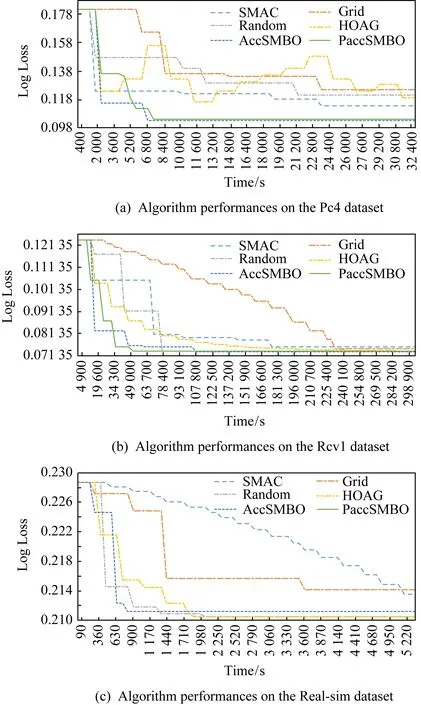
Fig. 7 Algorithm time performances on thedifferent dataset图7 不同算法在不同数据集上的时间性能
图6(c)和图7(c)展示了不同算法在Real-sim数据集上的实验结果.在串行算法的比较中,从代数上看,HOAG算法和串行AccSMBO算法都得到了最快的收敛速度并找到最佳超参.串行AccSMBO算法的收敛速度是SMAC算法的240%.并行AccSMBO算法(PaccSMBO算法)在收敛的代数上虽然在绝对的代数上比串行AccSMBO算法多,但是平均到每个worker,其消耗的代数会比串行AccSMBO更少,绝对时间会更快.从绝对时间上看,串行AccSMBO算法的收敛速度是HOAG算法收敛速度的109%,是SMAC算法收敛速度的260%.PaccSMBO算法的收敛速度是HOAG算法的145%,是SMAC算法的347%.
6 结 论

