一种面向边缘计算的高效异步联邦学习机制
2021-01-05芦效峰廖钰盈PietroLioPanHui
芦效峰 廖钰盈 Pietro Lio Pan Hui
1(北京邮电大学网络空间安全学院 北京 100876)
2(剑桥大学计算机实验室 英国剑桥 CB3 0FD)
3(香港科技大学计算机科学与工程学院 香港 999077)
机器学习已经逐步地改变我们生活、学习、工作的方式,其在语音、图像和文本识别[1],语言翻译等方面都取得巨大突破.谷歌、Facebook和苹果等大型公司从用户端收集大量训练数据,实现大规模的深度学习网络.虽然深度学习的实用性是不可否认的,但其使用的训练数据却可能涉及严重的隐私问题:数百万人的照片、视频被集中收集,这些数据被大公司永远地保存,用户既不能删除这些数据,也不能控制这些公司如何使用数据.其次,图像和视频中很可能包含大量敏感信息[2],如面孔、车牌、电脑屏幕、其他人的对话等.互联网巨头垄断这些“大数据”,独享数据背后巨大的经济效益.
众所周知,随着训练数据量的增大,多样化的增多,机器学习所训练的模型会变得更好.然而,在许多领域,尤其与医学相关的领域,法律规定不允许共享与个人相关的数据.自2017年6月1日《中华人民共和国网络安全法》开始实施,个人信息安全被列入重点保护范围,国家对隐私条款提出了明确的要求,进一步完善了对个人信息的保护.因此,相关行业的研究人员只能对属于他们自己机构的数据集进行分析和挖掘.如果单个组织(如特定的医疗诊所)所拥有的数据量不是非常大,并且相似度较高,多样化不足,则在这样的数据集上进行机器学习,研究人员最终可能得到扩展性较差的模型,或者容易产生过拟合的结果.在这种情况下,数据的隐私和机密性的限制明显影响了机器学习的效果.
另一方面,目前全球物联网进入了第3次发展浪潮.2018年全球物联网连接数约为80亿个[3],这些物联网设备产生大量的数据.在传统云计算架构中,这些数据需要集中传输到云端进行处理,这会加大网络负载,造成传输拥堵和数据处理的延迟.因此,传统云计算已经不适用于边缘物联网设备过多的情况.于是,一种新型的计算模型应运而生——边缘计算[4].边缘计算是指在靠近物或数据源头的一侧,就近提供计算、存储等服务.相比数据集中式的云计算模型,边缘计算在网络的边缘处理数据,这样能够降低网络带宽负载、减少请求响应时间、提升电池续航能力的同时保证数据的安全性和私密性.
然而,面向边缘网络的联邦学习在实现中面临诸多挑战.首先,面向边缘网络的联邦学习中,因为任何一个独立的边缘设备所拥有的数据都是有限的,所以单独训练时,每个参与者的学习模型都容易陷入局部最优.其次,联邦学习中节点学习的梯度数据间接反映了训练样本的信息,攻击者能从有效的梯度信息反推出样本数据,需要降低梯度通信量来降低隐私泄露的可能性.
针对以上挑战,本文提出一种面向边缘计算的高效异步联邦学习机制(efficient asynchronous federated learning mechanism for edge network computing, EAFLM),可以实现在不共享数据的前提下对多方数据进行学习,实现更自由更高效的联邦学习.相比传统的分布式学习,EAFLM各节点独立地在自己本地的数据集上进行训练,在不影响准确率的前提下赋予参与学习者更多的自由度和隐私保护.使用其他参与者学习的模型来优化本地学习的模型参数,可以有效地帮助每个参与者逃避局部最优并使他们能够探索其他值,从而产生更准确的模型.
本文探讨了异步联邦学习的不同情况,对边缘节点异步联邦学习提出了双重权重的解决方案.异步联邦学习旨在为边缘学习节点提供更自由的学习方式,且降低高自由度带来的精度损失.本文的主要贡献有3个方面:
1) 区别于现有的分布式学习系统,提出一种更适合边缘网络中离散节点协作学习的异步联邦学习机制,使节点在不共享隐私数据的前提下从数据中进行学习.
2) 在前人工作的基础上设计了一种阈值自适应的梯度压缩算法,在将梯度通信次数压缩至原通信次数的8.77%时,测试集上准确率仅降低0.03%.
3) 为了适应边缘节点在进行模型训练时间上的随机特性,对异步联邦学习进行深入的探索,提出了双重权重的方法来解决异步学习带来的性能降低问题.
1 相关工作
许多研究者在分布式机器学习方面做了大量工作,已经有基于云的大规模分布式系统投入使用.许多系统支持多种数据处理方案,包括模型并行和数据并行[9-10].
常见的分布式架构中包含数据中心,该数据中心一般以参数服务器的形式存在.参数服务器允许大量的学习节点在共享的全局神经网络模型上进行协作学习[11-12].这一研究领域专注于如何设计高效的服务器架构,快速处理大小为109~1012的向量.目前分布式学习的学习节点都是电脑等存储和计算较强且网络连接稳定的设备,对于诸如移动手机等性能较为波动的设备则少有关注.
联邦学习架构的出现吸引了许多学者的关注,其中关于Non-IID数据集和数据不平衡问题[13]是其中一大研究重点.而关于节点学习模式方面的研究一直都集中于同步学习算法,如McMahan等人[5]的联邦学习平均算法采取同步训练的方法;联邦学习中的隐私保护如差分隐私[8]和安全聚合[14]都需要在设备上进行同步操作,所以本质上还是属于同步训练的范畴.此外,研究人员开始尝试在车对车通信[15]和医疗应用[16]等领域实现联邦学习.
由于联邦学习需要与大量的学习节点进行梯度交互,而这些交互通信不仅带来巨大网络通信带宽,还存在安全隐患.有研究表明,可以通过从共享的梯度数据中获取隐私训练数据[17],研究者首先随机生成一对“虚拟的”输入和标签(dummy data and label),然后执行通常的前向传播和反向传播.从虚拟数据导出虚拟梯度之后,他们没有像传统优化那样更新模型权重,而是更新虚拟输入和标签,以最大程度地减小虚拟梯度和真实梯度之间的差异.当攻击结束后,私人数据便完全暴露了出来.值得注意的是,整个过程不需要训练数据集的任何额外信息.文中还给出一些能有效防止隐私泄露的方法,其中包括梯度量化和稀疏化.数据显示,当压缩率大于20%时,梯度压缩能有效地防止样本信息泄漏.
梯度量化和稀疏化不仅能保证样本数据的隐私安全,还能减轻网络的负载,克服分布式学习模型中的通信瓶颈[18].
梯度量化将梯度量化成低精度值以降低通信带宽.Frank等人[19]提出1-bit SGD(stochastic gradient descent)以减少梯度传输数据大小,并在传统语音应用中实现10倍加速.Dan等人[20]提出了另一种称为QSGD(quantized SGD)的方法,它平衡了准确度和梯度精度之间的权衡.类似于QSGD,Wen等人[21]开发了使用3-level梯度的TernGrad.这2项工作都展示了量化训练的收敛性.但是TernGrad仅对CNN进行了实验,QSGD也仅计算了RNN损失的精度.DoReFa-Net[22]尝试量化整个模型,包括梯度,使用1 b的权重和2 b的梯度量化.
Strom等人[23]使用阈值来实现梯度稀疏化——仅发送大于预先定义的恒定阈值的梯度.但是,在实践中阈值是难以选择的.因此,Dryden等人[24]分别选择了固定比例的正梯度和负梯度;Aji等人[25]提出了gradient dropping,使用单一绝对值阈值对梯度进行稀疏化.为了保持收敛速度,gradient dropping需要添加一个标准化层[26];gradient dropping可节省99%的梯度交换,同时在机器翻译任务中仅导致0.3%的BLEU损失;同时,Chen等人[27]提出根据局部梯度活动自动调整压缩率,并在数学上进行了证明,实现了对于完全连接层的200倍压缩,卷积层的40倍压缩,而在ImageNet数据集上降低的Top-1精度可忽略不计.Chen等人[28]提出了LAG(lazily aggregated gradient),自适应地对梯度进行计算并跳过部分梯度通信,以减少通信带宽并减轻服务器压力.基本原则是检测变化缓慢的梯度,并对这些梯度进行压缩.LAG很有参考价值,但对优化的问题进行了限制:优化问题是凸问题且是Lipschitz平滑的.
本文提出的EAFLM中的梯度压缩属于梯度通信稀疏化的范畴,但与前文提到的方案不同,在本文中无需探索一个最优的梯度阈值,因为寻找最优阈值的工作是困难的,且不同问题对应的阈值也是不同的,限定梯度阈值也会使得异步联邦学习框架的扩展性降低.
如果将学习对象扩散到边缘节点,同步训练变得难以实现且不切合现实需求.虽然也有少数学者采用了异步学习方法,但仅是将异步作为一种正则化方法[29],缺少对异步联邦学习进行详细系统的研究,而且在大多数研究中各异步联邦学习参与节点所处的学习轮数是相差无几的,实质上还是当作同步联邦学习研究的.异步联邦学习中各节点学习轮数相差较大,甚至学习进程是完全错开的,这跟同步联邦学习情况是截然不同的.联邦学习过程由并联到串联的转变,不仅增加了总体学习时间,降低学习效率,还影响人工智能模型的精度,而这类型的异步联邦学习问题目前仍缺乏关注.本文对这类型的异步联邦学习问题进行了研究,降低了由异步联邦学习带来的精度损失.
2 一种面向边缘计算的高效异步联邦学习机制
2.1 联邦学习机制
联邦学习(federated learning)是一种新兴的人工智能基础技术,其设计目标是在保障终端数据和个人数据安全的前提下,在多参与方或多计算节点之间开展高效率的机器学习.其中,联邦学习可使用的机器学习算法不局限于神经网络,还包括随机森林等重要算法.
如图1所示,联邦学习机制由1个参数服务器和多个边缘节点组成,参数服务器负责收集各参加节点上传的梯度,根据优化算法对模型各参数进行更新,维护全局参数;参与节点独立地对本地拥有的敏感数据集进行学习.每轮学习结束后,节点将计算的梯度数据上传至参数服务器,由服务器进行汇总更新全局参数.然后节点从参数服务器下载更新后的参数,覆盖本地模型参数,进行下一轮迭代.整个学习过程中,节点只与参数服务器通信,除了共同维护的全局参数外节点无法获取有关其余节点的任何信息,保障隐私数据的机密性.
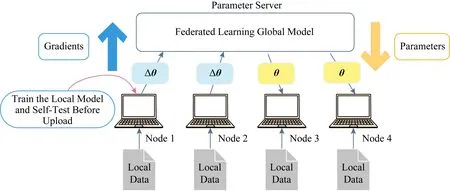
Fig. 1 Schematic diagram of the federal learning mechanism图1 联邦学习机制示意图
2.2 结构介绍
面向边缘网络的联邦学习需要与多个边缘学习节点进行模型数据的交互,这带来高昂的通信代价.经研究发现分布式SGD中99.9%的梯度交换是冗余的,当参与学习的边缘节点数量增多时,这些冗余的梯度所需要的通信成本是不可忽视的,而且会给予参数服务器较大的通信压力,跳过节点的部分通信能有助于减轻通信负荷.且在联邦学习中,节点在执行梯度通信前会停止训练直至获得返回的最新参数,因此,梯度压缩还有助于减少联邦学习的总体模型训练时间.
图2所示为面向边缘网络计算的高效异步联邦学习机制框架图,框架分为参数服务器层和边缘节点层,其中阈值自适应模块处于边缘节点层,异步联邦学习模块横跨2层.

Fig. 2 Asynchronous federated learning mechanism foredge network computing图2 面向边缘网络计算的高效异步联邦学习框架
阈值自适应模块分为自适应阈值计算和梯度通信压缩2个子模块,分别负责根据最新参数变化计算阈值和使用阈值对不符合的梯度通信进行压缩.
由于边缘节点具有高度自由性,因此强迫所有节点同时进行训练变得不切实际.异步联邦学习则分为4个子模块:参数更新、梯度修正、双重权重计算和节点学习状态监控.节点学习状态监控子模块负责监控节点学习状态如学习所处的轮数与样本数量等;双重权重计算子模块根据节点学习信息计算对应的样本权重和参数权重,具体计算方法在第4节进行介绍;梯度修正子模块将节点上传的梯度根据双重权重进行修正;而修正完的梯度则被用于参数更新子模块进行全局参数更新.
阈值自适应模块与异步联邦学习模块不是相互独立的,自适应的阈值计算需要获取更新后的参数,并与历史参数进行比较.而压缩后的梯度通信影响了节点学习状态,进而影响双重权重的计算.
3 阈值自适应梯度压缩
3.1 阈值自适应梯度压缩原理说明
梯度压缩是指对节点与服务器之间的梯度通信进行压缩,即压缩单个节点与参数服务器的通信次数.在前人的工作中,无论是简单地引入通信压缩率,还是根据固定阈值作为梯度检查的判别条件,都存在诸多不足之处.因为不同学习过程中梯度变化程度是不同的,简单地根据压缩率随机选取压缩的节点容易忽略拥有较大信息量的梯度,对全局模型训练造成影响;而固定阈值则会对梯度通信进行过度压缩,在训练的后期造成模型波动不易收敛的结果.
在EAFLM中,节点自动适应模型训练过程中每轮梯度的变化,计算出合适的阈值来对梯度通信进行压缩.只有符合条件的节点才能获取对应轮次的与参数服务器通信的资格,否则在本地累计梯度信息,进行下一轮学习迭代,最终梯度会累计足够的信息量上传到参数服务器.无论节点是否获得该轮的通信资格,在下一轮学习结束后都要进行梯度检查,即梯度检查是贯穿节点的整个学习过程.
3.2 梯度压缩自检式数学推导
本文对梯度压缩中的自检表达式进行研究,并在数学上进行了推导验证.
表1对本文所涉及的符号进行解释:

Table 1 The Meaning of the Symbol表1 公式中符号的表示含义



(1)
“懒惰”节点的定义可以说是阈值自适应梯度压缩的关键部分,不同的定义不仅会导致被忽略的信息量的不同和算法的压缩率,还会影响模型的准确率.在本文中,“懒惰”节点集合ML满足:
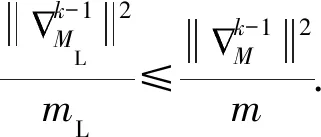
(2)
设更新参数的优化算法为梯度下降算法(gradient descent),即:

(3)
其中,α是学习率.将式(3)代入式(2)可得:

(4)
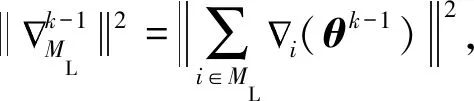
(5)
若节点i∈ML满足式(6),则式(2)一定能被满足:
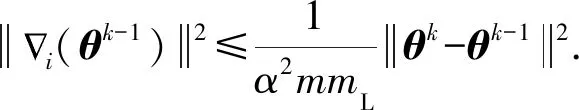
(6)
由于集合ML的总数无法事先获取,所以为了简化问题,我们引入比例系数β来衡量集合ML的节点总数,即mL=βm.整理式(6)可得:
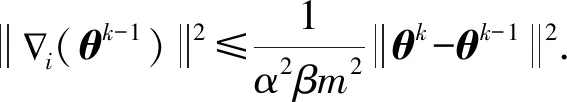
(7)
θk-θk-1的获取是困难的,但由于学习过程中参数变化趋于平滑,因此本文将θk-θk-1近似为
(8)

将式(8)代入式(7)可得:
(9)
式(9)为节点进行梯度检查的自检表达式,即节点在1轮学习结束之后执行自检操作.需注意的是,不满足式(9)则与参数服务器通信;满足则跳过本轮通信,本地累计梯度,继续执行下一轮学习.
相较于传统联邦学习,本文的方法对网络带宽等设备配置的依赖性较小.因为带宽影响了节点传输时间,较低的带宽会导致节点每轮学习时间的增大,从而延长总体学习时间,因此若要控制总体学习时间,则需对带宽配置进行限制.但经梯度压缩后的联邦学习中梯度通信次数减少,受带宽影响的轮数也随之降低,因此理论上,本文的方法对带宽等配置的需求与未压缩的传统方法来比较小,能更好地适应带宽有限的网络.
4 面向边缘网络的高效异步联邦学习
EAFLM面向的对象是高度自由的边缘节点,有许多因素都会引起异步学习,如加入学习的时间不同、节点的计算力不同(相同训练任务所需的时间不相同)、梯度压缩、由各种外部因素导致的学习中断等.本文提出参数权重来解决异步联邦学习问题.
4.1 异步联邦学习存在的问题
异步联邦学习中节点存在学习样本不均、学习进度各异等问题.如图3所示,图3中直线表示当前时间,浅色部分表示已经完成的学习任务,深色带底纹部分表示还未进行的学习任务.所有节点的学习总轮数是相同的,与时间线交差的部分表示当前所处的迭代轮次.图中的各个节点是处于学习的不同阶段,如节点1处于学习进程的50%,若总轮数为1 000轮,则节点1处于第501轮.
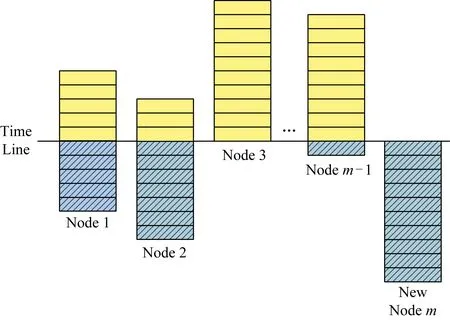
Fig. 3 Asynchronous federated learning图3 异步联邦学习
样本数量可以一定程度上反映样本多样性,基于高复杂度数据训练的模型具有更好的扩展性.而模型训练的过程可以理解为模型的“学习”的过程,一般地,随着时间的推移,模型越接近问题的最优解.如图3中,这些节点与学习问题最优解的距离是不同的,因此这些差异较大的的节点对参数服务器中的全局参数进行平等的更新显然是不合理的.我们引入双重权重来解决异步学习中节点学习状态不均衡的问题.
4.2 双重权重修正的异步联邦学习
面向边缘网络计算的高效异步联邦学习机制的权重分为2部分:样本权重和参数权重.样本权重是由节点的样本数量与总样本数量的占比决定,而参数权重则受梯度的目标参数与当前全局参数在时间上的相近程度所影响.
定义1.样本权重.代表一个节点所拥有的样本与总节点的样本总数的占比大小.
n个学习节点的集合为N={N1,N2,…,Nn},其中每个节点对应的样本数用Di表示.节点i的样本权重可由节点的样本数与总样本数求得:

(10)

定义2.参数权重.表示节点优化的参数与当前的全局参数在时间先后顺序上相差的程度.
从参数服务器的角度看整个联邦学习是一次次的参数优化更新,不间断地有节点向参数服务器提出下载最新参数的请求,又不停地有节点上传新的梯度以更新参数,简化的过程如图4所示:
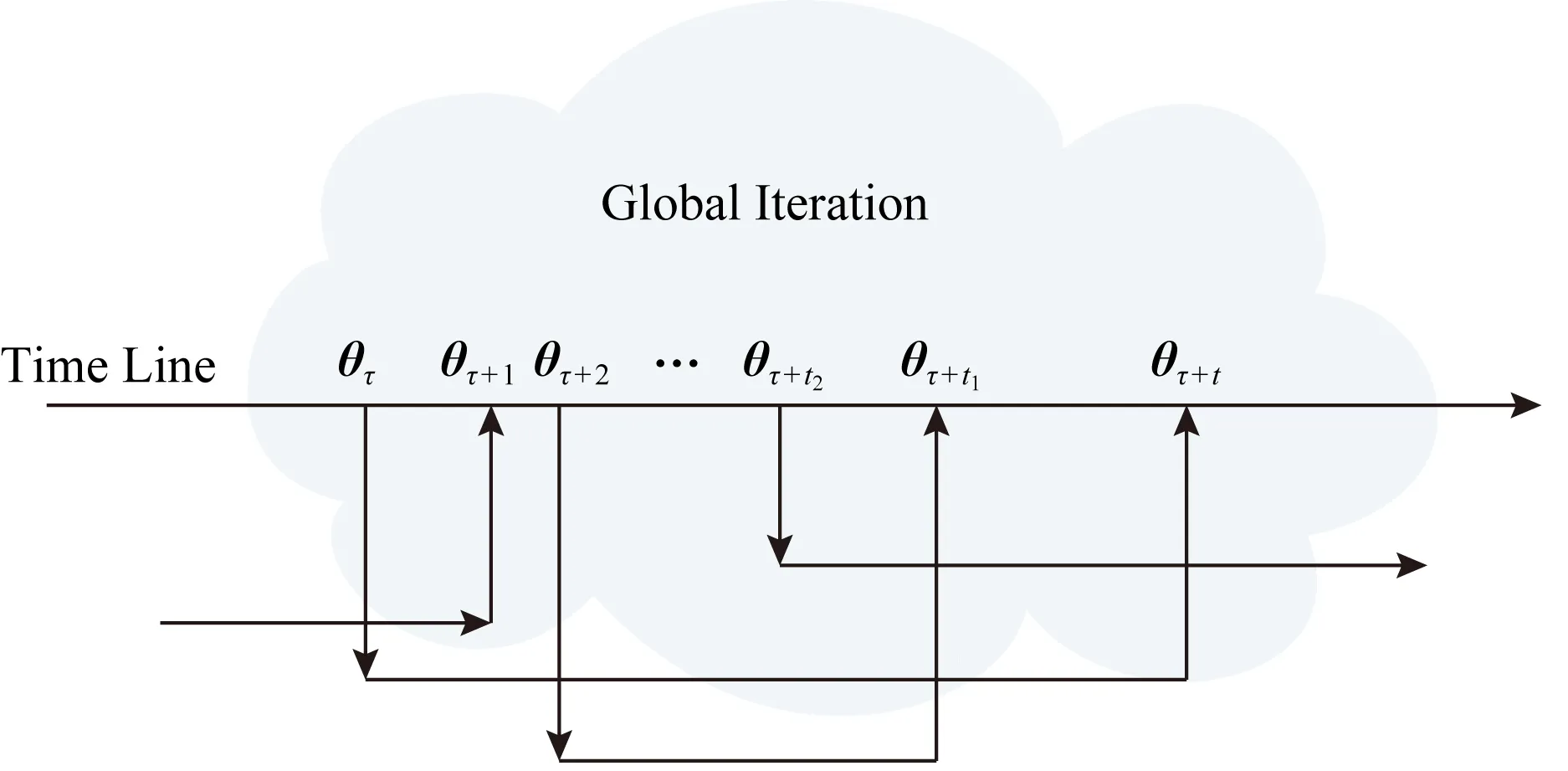
Fig. 4 Asynchronous federated learning and parameters staleness图4 异步联邦学习与参数陈旧度
每个节点在下载最新参数到上传对应的梯度之间的时间内都有其他节点的上传操作穿插其中.在图4描述的参数优化过程中梯度具有一定的陈旧性,令参数陈旧度为
μstaleness=Iupload-Idownload.
(11)
在图4的例子中,在节点下载和上传梯度的时间间隔内,其他节点会上传新的梯度,参数服务器会进行梯度的更新,参数陈旧度表示了节点在完成一次迭代学习中参数服务器经过了几轮更新,这一定程度地反映了节点的计算能力.为了使陈旧度越大的节点其参数权重越小,且衰减的过程相对平缓,本文选择底数小于1的指数函数作为参数权重的衰减函数:
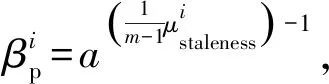
(12)
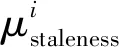
双重权重修正为

(13)
其中,θ是原始模型参数,θ′是修正后的模型参数.
在异步学习过程中,边缘节点提交的梯度在参数服务器上要经过双重权重的修正才能参与全局模型优化.修正后的梯度根据具体的优化算法更新全局参数,优化结束后,节点获得最新的参数并将其覆盖本地参数,进行下一轮迭代学习.
异步联邦学习对于网络性能的波动也具有很好的适应性,当某个节点的网络质量变差时,势必会影响节点学习的进程,造成各个节点学习进度各异.相较于传统联邦学习,基于双重权重修正的异步联邦学习对这些进度各异的节点贡献的梯度根据其学习程度进行修正,减小如网络性能波动造成的学习精度的影响,对性能不稳定的网络具有一定的鲁棒性.
5 实验结果
5.1 实验配置
为了模拟实际场景,我们搭建如下实验环境:计算力较强的GPU服务器作为参数服务器,负责大部分计算工作;其余多台电脑模拟边缘网络中的单个学习节点,各自独立地进行联邦学习,带宽为1 Mbps.参数服务器与节点之间的通信使用Thrift框架.每台电脑本地存放部分数据(在我们模拟的实验中,每个节点的数据占总数据量的0.2%),独自根据本地数据训练神经网络模型.本文研究的对象是多个边缘设备节点,这些节点的计算力各不相同,通过加入停顿间隔时间来模拟这些算力不同的设备.为了更好地模拟实验场景,这些电脑上的联邦学习都由一台独立的电脑统一控制.
实验环境如图5所示,其中Order表示m个节点启动顺序,Interval表示节点从相邻2轮学习间隔停顿的时间.在初始化阶段,管理节点根据节点总数生成乱序序列Order(如图5中的{4,1,6,9,…,5}),并对应生成随机序列Interval(如图5中的{16.20,46.46,62.97,325.62,…,24.048}(s)).初始结束后,管理节点根据Order:Interval序列对启动对应节点.
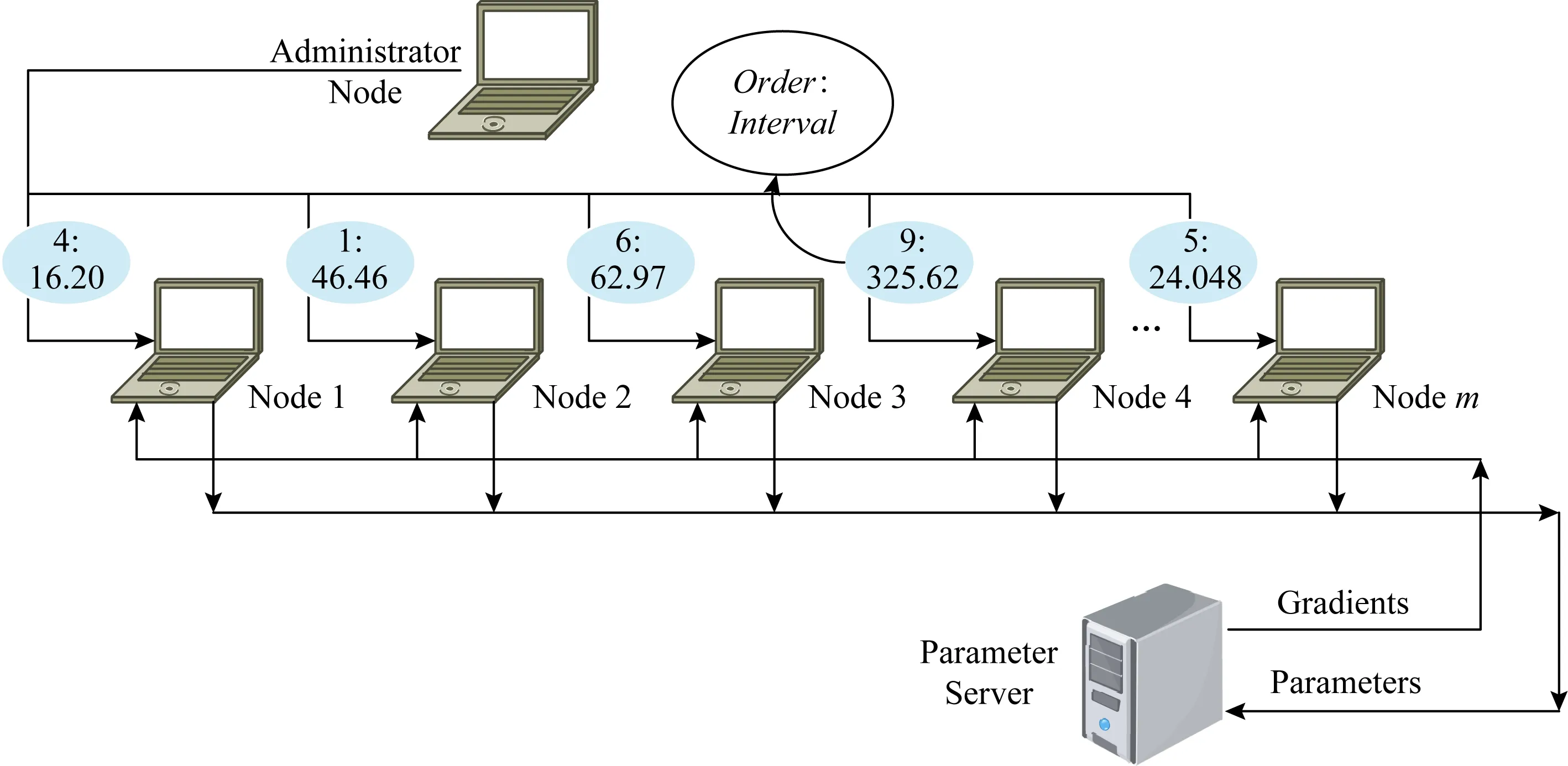
Fig. 5 Experiment configurations图5 实验配置
5.2 实验指标
实验部分采用的评价指标为准确率(accuracy,Acc),压缩率(compression ratio,CR)和压缩平衡指数(compression balance index,CBI),其中准确率Acc是指Top-1 Accuracy.
压缩率CR反映梯度压缩的压缩程度,压缩率越小,压缩程度越高.

(14)
一般地,压缩率的减小会导致准确率的逐渐降低.如何在2个指标中权衡,做出最佳决策成为难题.因此本文引入压缩平衡指数CBI,表示梯度压缩综合效果,
CBI=α1×Acc+α2×(1-CR),
(15)
其中,α1,α2是用于衡量Acc和CR重要性的2个可调节参数,α1+α2=1,α1>0,α2>0.若在现实情况中,Acc优先级高于CR,则可设置α1>α2;反之,则α1<α2;若两者优先级相同,则α1=α2.CBI值越高表示梯度压缩综合效果越好.
5.3 梯度压缩实验
我们在MNIST数据集上评估EAFLM的梯度压缩性能,MNIST数据集是一个手写体数据集,共有6万个训练样本和1万个测试样本.本文对格式为32×32的图像进行归一化,使得数字位于图像的中心.
在这部分实验中共有3个学习节点,节点训练的模型结构参考了Tensorflow官网中的Tutorial,我们未对模型结构进行调整.模型结构为3层MLP模型,每层的神经元个数分别为256,256,10.本次实验将数据集平均分为3份,学习节点随机获得其中的1份.在每次实验中,节点都会重新获取新的数据.我们对不同参数β分别进行实验,并对最终结果求平均值.
补充说明:本文的研究重点是联邦学习框架中的通信,未对模型结构和优化算法进行过多研究,因此本文实验中出现的过拟合等问题其背后的原因及解决方案不属于本文研究范围.同样地,准确率等实验指标仅是为了对比各方法的性能,不对模型的优劣进行评估.且由于不同方法的对比实验采用相同的配置,实验中的指标仍具有可用于比较的价值.EAFLM不对学习模型进行限制,因此在现实运用中使用者可以根据实际学习问题对模型结构和实验参数进行调整.
5.3.1 梯度压缩实验分析——压缩率及准确率
表2表示不同β取值对压缩率及准确率的影响.从整体上来看,随着β值的减小,压缩率也逐渐减小,即压缩程度增大.而随着梯度通信逐渐被压缩,准确率也随之降低.从表2中也可看出数据存在一定的波动,这是由于不同对比组的实验设置(如样本序号和初始模型参数)的不同导致模型训练结果存在个体差异,且实验模型参数初始值不同也是造成数据小范围抖动的原因之一.但明显地,在β∈[0.1,0.2]区间时,压缩率存在明显的上升,而在β∈[0.2,1]区间内,压缩率上升幅度较小,因此在图8中,我们着重展示的是β∈[0.1,0.2]区间.
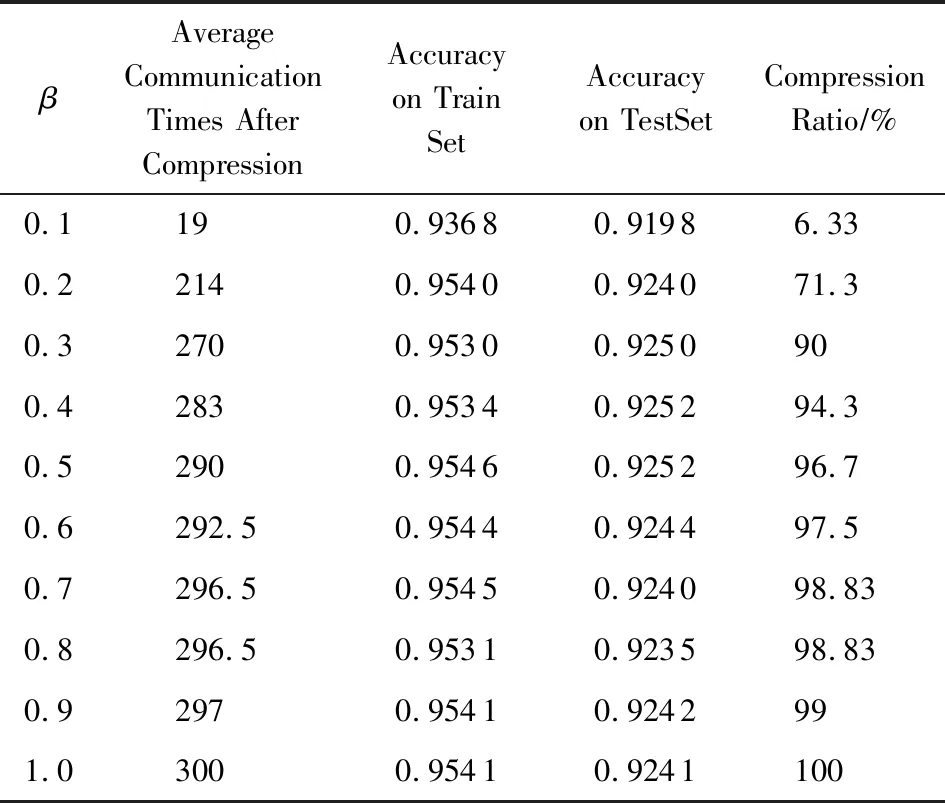
Table 2 Compression and Accuracy Under Different β表2 不同β值下的压缩率及准确率
图6为10组不同超参数(样本序号和停顿间隔时间)下对比实验的结果,图6(a)浅色细线条和图6(b)浅色细线条分别为10次实验中在测试集和训练集上的具体数据波动,对应的图6(a)深色加粗线条和图6(b)深色加粗线条为测试集和训练集10次实验的平均数据.

Fig. 6 Different β values and model accuracy on data sets图6 梯度压缩中不同β取值在数据集上的准确率
在图6中,10组实验数据虽然在个体上存在波动,但总体上呈现出随着压缩率的增大,准确率随之上升,这也可从对应的深色加粗线条看出.有趣的是,图6(a)中可看出,在β∈[0.14,1]区间内(对应图6(b)的区间则为β∈[0.13,1]),梯度压缩对准确率的影响不大,且出现了波动,这是因为所选的学习模型已达到最大的学习效果.明显地,冗余梯度通信对达到饱和学习的模型的增益较小,梯度压缩有助于提高联邦学习的性能.在图7中,随着β的增大,梯度通信次数在不断增大,压缩率也随之增大.

Fig. 7 Different β and communications times图7 梯度压缩中不同β取值对通信次数的影响
5.3.2 梯度压缩实验分析——压缩平衡指数
为了选择最佳β值,本文对β∈[0.1,0.2]区间中的实验数据计算CBI值,计算结果如图8所示.结合图8可以发现本文实验中最佳β值为0.1.
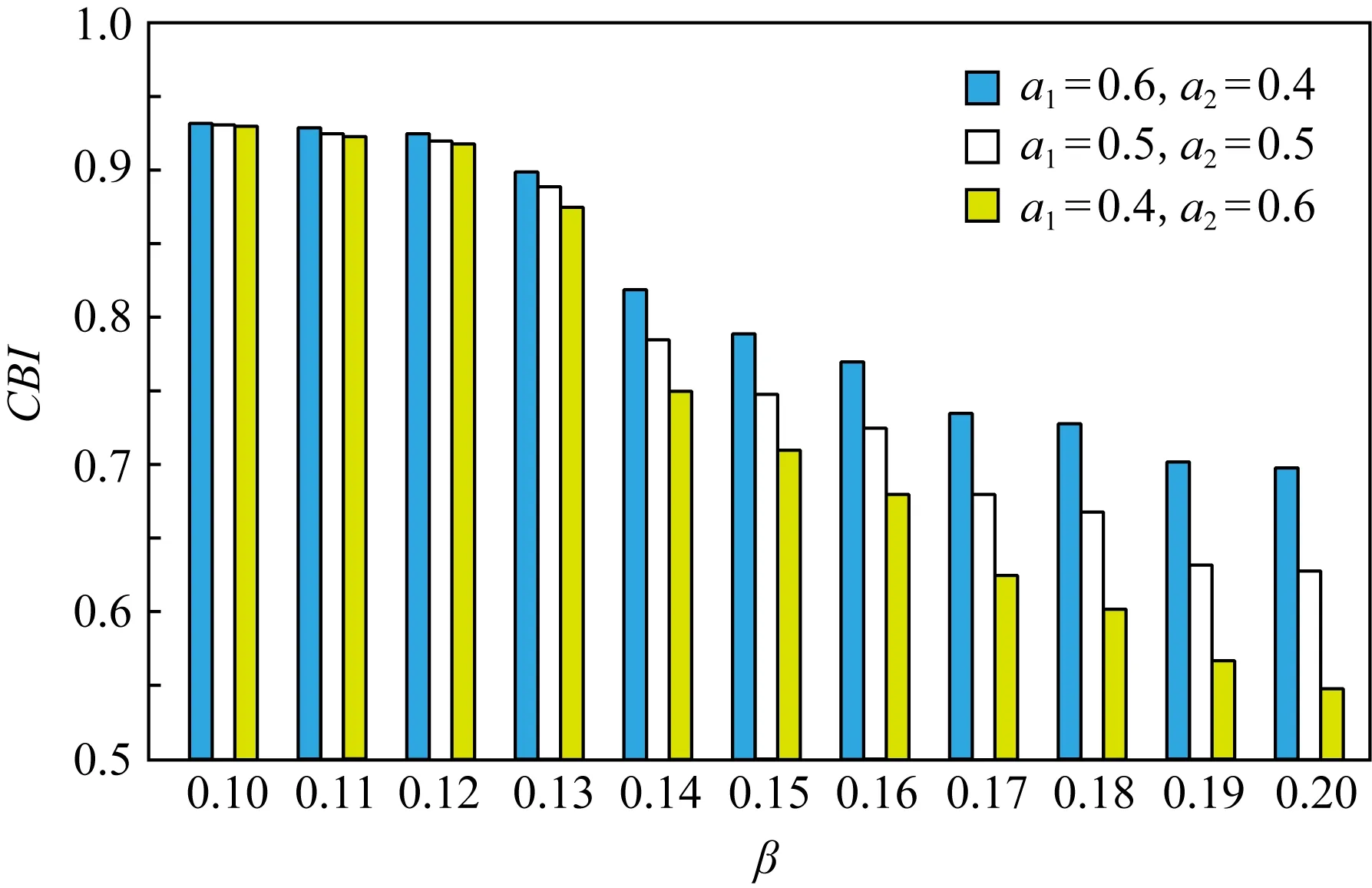
Fig. 8 CBI of different β values in gradient compression图8 梯度压缩中不同β取值下的CBI值
我们对Chen等人[28]的工作(LAG)做了对比实验,表3从准确率、压缩率、压缩平衡指数3个方面展示了EAFLM中阈值自适应梯度压缩算法与LAG算法的性能比较.从表3可看出LAG的压缩率比β=0.1和β=0.11 EAFLM的压缩率低,压缩程度较高.但无论是在训练集还是测试集上,准确率都比EAFLM低.为了进一步比较两者性能,我们取3组不同的a1,a2组合计算CBI.从表3可看出,除了在a1=0.4,a2=0.6时,LAG的CBI比β=0.11 EAFLM高,其余两者情况下,EAFLM性能都高于LAG,β=0.1的EAFLM更是3种情况下都优于LAG.且在EAFLM中,根据不同的实际需求调节β的取值,以达到最佳的压缩程度.
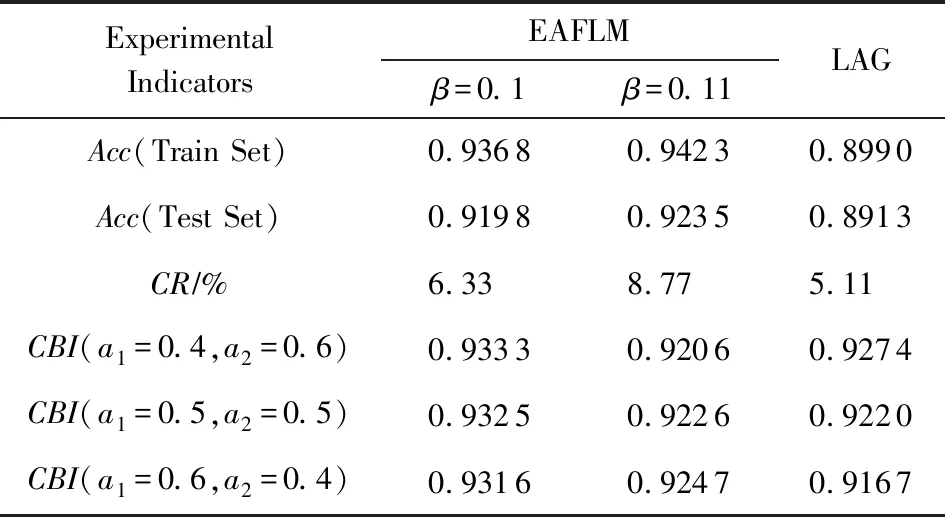
Table 3 Performance Comparison Between Different β Values of EAFLM and LAG表3 不同β值下的EAFLM与LAG的性能对比
5.4 异步联邦学习
为了使异步学习实验效果更加显著,异步学习这部分的实验数据采用Cifar10数据集,CIFAR-10数据集由10个类的60 000个32×32彩色图像组成,每个类有6 000个图像.有50 000个训练图像和10 000个测试图像.我们将训练集平均分为500份,每次实验开始前,节点随机从中挑选一份数据进行训练为了模拟异步联邦学习,学习节点的数量增加到10个.除此之外,本实验在图5的基础上增加停顿时间,即每个节点在1轮训练结束后停顿一段时间.停顿时间序列由管理节点生成.同样地,本次实验采用了Tensor-flow官网Tutorial中的卷积网络代码,模型结构为5层卷积网络模型.由于异步联邦学习对象是高自由度的边缘设备,这些节点无法像服务器等设备一样稳定、长时间地训练网络模型.因此为了模拟这种情况,我们将训练轮数设置为500轮.学习轮数的减小使得实验中总体的准确率都不高,这可以通过调参等方法来提高准确率,这里不予过多讨论.实验中设置的超参数数值仅供参考,实际运用中仍需根据具体问题进行设置调整.
我们分别随机选取5组不同的超参数组(子样本集序号、停顿时间)进行3个对比实验,分别是节点训练中无停顿(对应表4中的Synchronous)、节点训练中有停顿(Asynchronous)和在双重权重下的训练中有停顿(EAFLM).在我们查阅的文献范围内,没有发现其他学者针对异步联邦学习进行算法上的改进,因此本文无法与更多方法进行对比实验.
表4为3种算法在训练集和测试集中的5组不同超参数组合实验的平均准确率.从表4可看出异步学习比同步学习具有较好的性能,这可以理解为异步类似于一项正则化处理,能一定程度防止学习的过拟合.在训练集上,对比同步联邦学习和异步联邦学习,EAFLM机制实现了5.1%和4%的准确率提升;而在测试集上,EAFLM的准确率分别提升了0.36%和0.15%.

Table 4 Asynchronous Experiment Performance on Data Sets表4 异步实验在数据集上的准确率
5.5 综合实验分析——梯度压缩与异步联邦学习结合
综合实验部分仍然采用与异步联邦学习部分相同的实验配置,我们选取了5种不同β值下的EAFLM与异步联邦学习进行对比实验,其中异步联邦学习是无梯度压缩和权重修正.表5从准确率、压缩率、压缩平衡指数3个方面展示了EAFLM与异步学习算法的综合性能比较.从表5可以看出,当β=0.5时,在准确率方面,异步联邦学习与EAFLM基本相当,但异步联邦学习在压缩和综合性能方面都比EAFLM差.在压缩率方面,β∈[0.2,0.5]下的EAFLM都相差不大,但EAFLM在β=0.1时,CR=75.1%,即相对于异步联邦学习算法来说,EAFLM进一步节省了24.9%的通信成本,但在训练集和测试集上的准确率仅降低10.5%和3%.在3组不同的a1,a2组合计算的CBI中,不同β取值下的EAFLM都比异步联邦学习高,因此,本次实验结果显示EAFLM的综合性能比异步联邦学习有所提高,其中β=0.1时,EAFLM的综合性能达到最优.
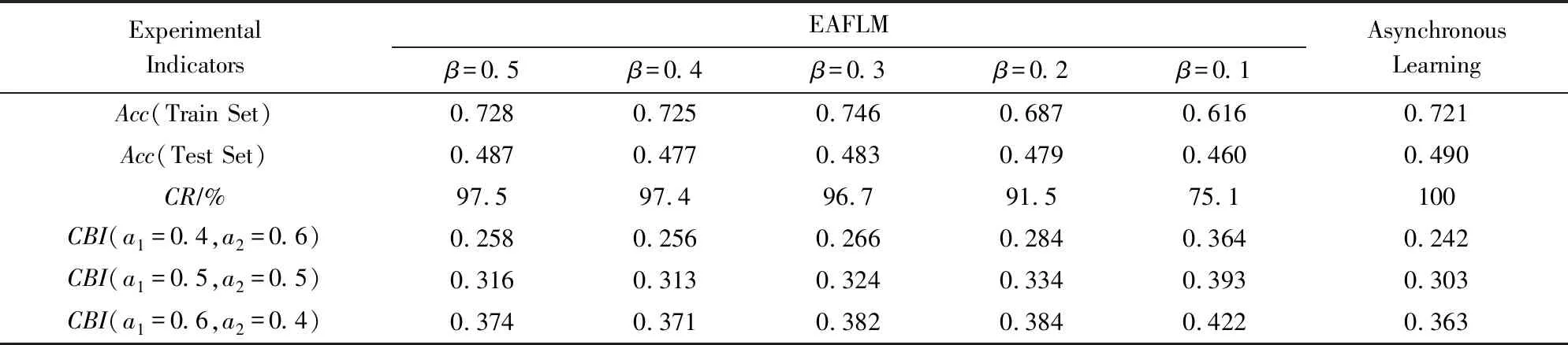
Table 5 Performance Comparison Between Different β Values of Comprehensive EAFLM and Asynchronous Federated Learning表5 不同β值下的综合EAFLM与异步学习的性能对比
6 总 结
本文提出一种面向边缘网络计算的高效异步联邦学习机制(EAFLM)可以满足在不共享隐私数据的前提下对多方数据进行学习的这个现实需求,以实现更自由高效的联邦学习.EAFLM在不影响准确率的情况下赋予参与学习者更多的自由度和隐私保护.参与者在本地对拥有的数据集进行学习,在1轮训练之后,参与者根据自检条件来检查本轮是否满足与参数服务器通信的条件,若满足则将梯度上传至参数服务器.所有节点都是异步地执行以上步骤,不用等待其余节点,也无须同步学习轮次.整个学习过程中,节点只与参数服务器通信,除了共同维护的全局参数外节点无法获取有关其余节点的任何信息.
本文从阈值自适应梯度压缩和异步学习2大方面对EAFLM进行阐述,并进行相关实验.我们提出的阈值自适应梯度压缩算法,可以自适应模型训练过程中每轮梯度的变化,计算出合适的阈值来对梯度通信进行压缩.由于梯度数据间接反映了节点样本信息,攻击者能从有效的梯度信息反推出样本数据,减少梯度通信能有效地降低隐私泄露的可能性.测试集上,本文实现了将梯度通信压缩至原通信次数的8.77%时,准确率仅降低0.03%.
在异步联邦学习中,节点存在学习样本不均、学习进度各异等问题.这些差异较大的节点对参数服务器中的全局参数进行平等的更新显然是不合理的,因此我们引入双重权重来解决异步学习中节点学习状态不均衡的问题.实验表示在训练集上,对比同步联邦学习和异步联邦学习,EAFLM机制实现了5.1%和4%的准确率提升;而在测试集上,EAFLM的准确率分别提升了0.36%和0.15%.
我们的工作也存在不足之处,在阈值自适应梯度压缩中,执行梯度检查是牺牲单个节点本地计算时间来减少全局通信时间的典型例子.在众多神经网络学习中,学习迭代的轮数都是较大,轮数上万也并不少见,因此每轮结束都对梯度进行检查带来的计算时间无疑也是不容忽视的.为了缓解本地计算量,我们可以在上文描述的梯度压缩的基础上增加一个“免检”机制,这有助于减轻梯度检查带来的计算工作.在未来的工作中,我们将进一步对“免检”机制进行研究.
