钢-混结合梁桥主梁顶升施工时双柱式花瓶桥墩空间受力分析

熊振明

(武汉市政工程设计研究院有限责任公司，湖北 武汉 430015)

随着我国社会经济水平的高速发展，人们对桥梁美观要求越来越高，在市政桥梁建设中，花瓶墩的应用也越广泛，但是由于花瓶墩墩顶的支座作用边缘线越过墩底线等特点，受力比较复杂，不再满足梁式结构平截面假定，特别是双柱式花瓶墩，国内外现有对双柱式花瓶墩的研究分析较少，在国内的市政桥梁设计和施工中，很容易引用JTG 3362-2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[1](下文简称《规范》)中的拉压杆模型来计算此类桥墩系杆力，且施工时由于受条件限制的影响也很容易选择在墩顶进行顶升，为准确运用拉压杆模型适用条件和明确施工措施中的利弊，故有必要结合工程实例对此类型桥墩做进一步三维有限元受力分析。

以下以探明施工过程中产生裂缝为切入点，借助有限元的实体分析，重点分析双柱式花瓶墩在成桥状态和顶升状态时的受力特点，通过文中的计算方法算得的结果同《规范》中拉压杆模型计算结果做对比，得出结论后，简要交待裂缝分析结果并采取适当处理措施。

1 概 述

某高架桥是市区内通往对外窗口区域的重要快速通道，桥梁全长为3061.3 m。共分两个标段，本标段主线高架桥长2034 m，共布设26联95跨。主线高架桥标准段桥宽为22 m和18 m两种，均为双向四车道。本文论述分析的部分为该标段的第14联，该联上构跨径布置为40+59+40 m三跨连续变高度钢-混凝土结合梁，全联长139 m。边支座处梁高1.8 m，中支座处梁高3.5 m，单箱三室，两侧悬臂长度为3.5 m，桥梁宽22 m，本次分析的受该梁影响的下构桥墩为第51号墩(中央墩)，为该梁的中支点。

该桥墩采用钢筋混凝土双柱式花瓶墩，墩柱直线段横截面为1.6 m×2.0 m，为矩形截面，截面的四个边角设半径为0.1 m的圆弧倒角，横桥向墩柱的上端外侧采用弧线加宽至2.1 m形成花瓶形，其顶部设1.8 m(宽)×1.2～1.6 m(高)的横系梁连接。支座间距为5.5 m，墩高H为12.43 m，承台尺寸：6.8 m×6.8 m，承台下设置双排直径为1.5 m的桩基共4根，桩长42 m。桥墩结构如图1所示。

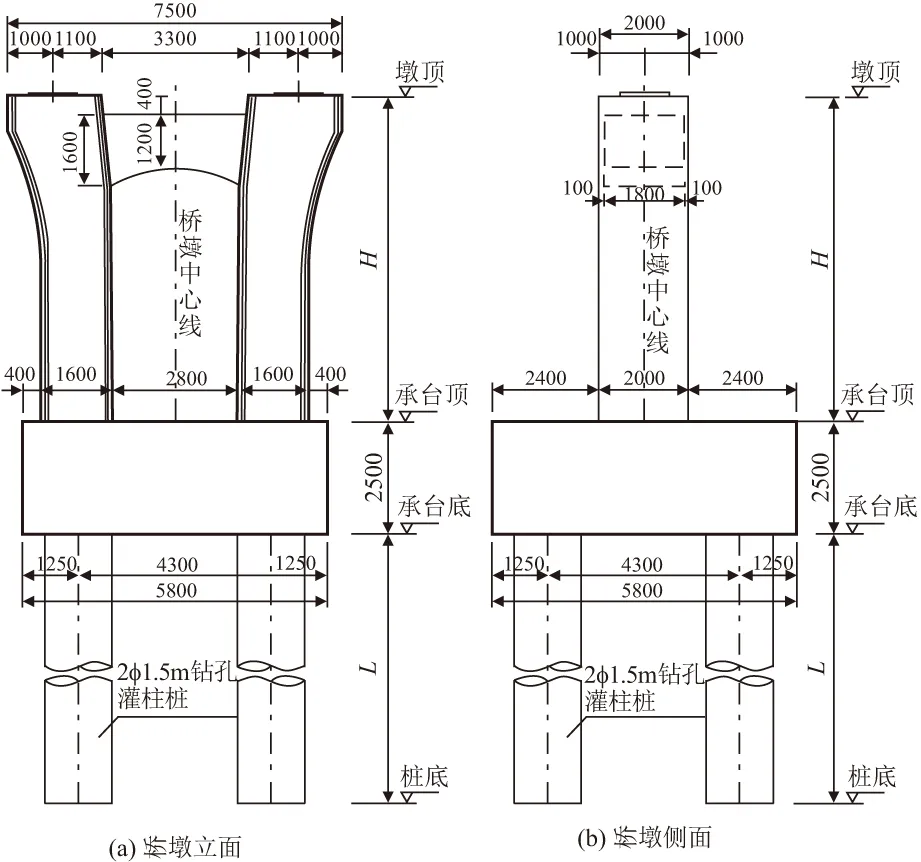
图1 桥墩结构/mm

在施工过程中，为在该钢-混结合梁中支点处的混凝土桥面板提供预压力[2]，在中支点处将梁临时顶升。由于在承台上搭设临时支架钢管作为顶升的临时支撑点时，其位于梁底正下方，吊机等架设器械无足够的工作空间，故在墩顶垫石两侧临时安装千斤顶，再借助钢垫板重复式垫高的方式使梁顶升。另由于千斤顶布置空间不够，将垫石纵桥向两侧均凿除部分，共安装了4个千斤顶(如图2a所示)，同时在该墩的另一柱顶同一位置也如同设置，并由电脑同步控制进行顶升。达到顶升高度后，千斤顶卸载，上部荷载均转移至两处临时钢垫板上(如图2b所示)。详见图2所示现场施工照片。当主梁顶升到位后，此时钢板下墩顶靠内侧混凝土表层出现竖向裂缝，局部裂缝长度达约10 cm。可能存在局部应力过大，或在复杂的墩顶受力中此处受到较大的拉应力而导致的开裂，因为该墩的受力配筋均满足《规范》要求，故有必要用更精细的三维有限元模拟做进一步验算。

图2 现场施工照片

2 有限元分析

由于花瓶墩受力复杂，初等梁理论已不再适用，本文采用大型空间结构分析软件Midas FEA软件对桥墩进行空间受力分析。

为明确该桥墩在施工过程中由于墩顶支撑点的位置和荷载作用不同而引起的受力变化，先分析桥墩在成桥状态下的受力特点。

2.1 模型建立

利用该软件建立桥墩的有限元模型进行三维非线性分析。以横桥向为x轴，顺桥向为y轴，竖向向上为z轴，桥墩混凝土采用8节点六面体实体单元模拟[3,4]，建模时不考虑普通钢筋作用，假设桩基底约束为固结约束。墩顶支座垫石与墩顶刚接。模型共分实体单元29400个。成桥状态下单个支座反力为14900 kN，支座垫石尺寸为1.3 m×1.3 m，模型中支点反力的反向作用力以3D单元面法向面力的形式模拟施加到支座垫石上，面压力P为8816568.05 N/m2，如图3所示。

图3 成桥状态下有限元模型

2.2 成桥状态下桥墩受力分析

对模型的墩柱、系梁、垫石材质赋予混凝土标号为C40，承台桩基混凝土标号为C35，经计算得到整个桥墩各实体单元应力值，其中最大主拉应力云图如图4所示。

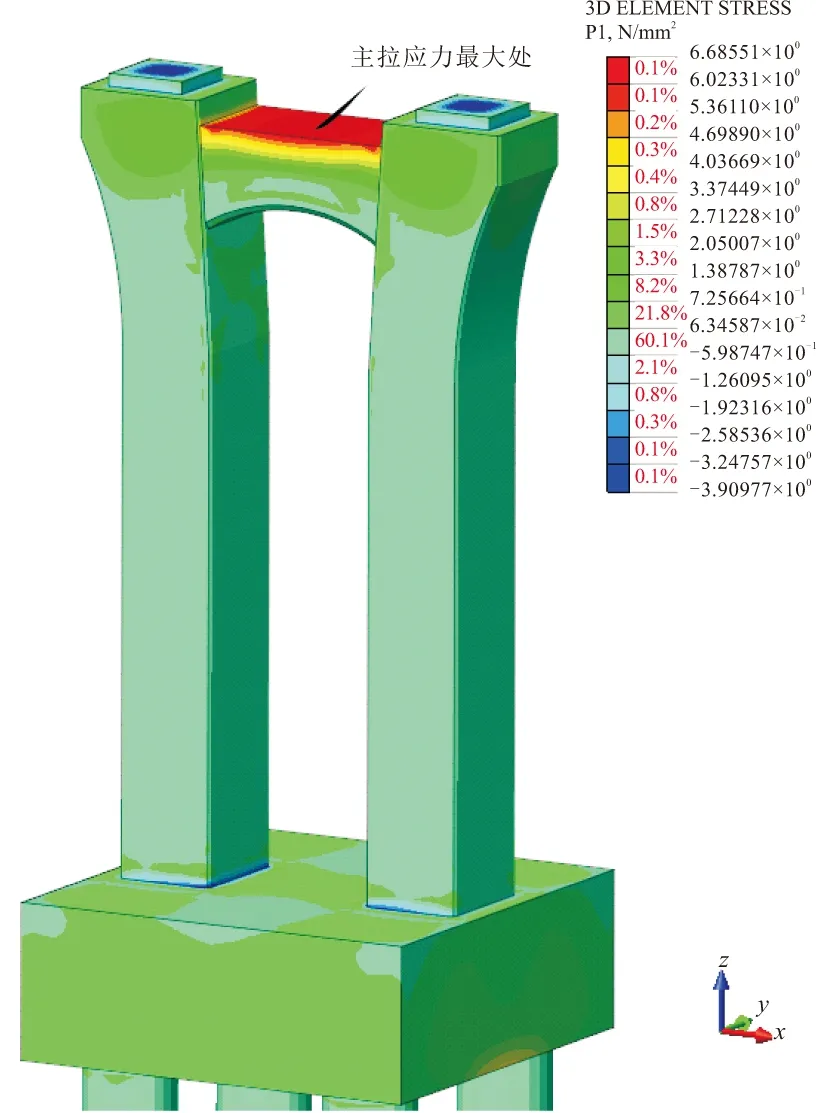
图4 全桥墩主拉应力云图

从图4可以看出，最不利位置基本出现在墩顶，故本文只对墩顶位置进行受力分析，其它构件的受力不做详述。现通过实体单元计算的应力进行积分求出截面内力，再根据求出的内力进行配筋并验算[3,4]。另外由于受压区受力不作控制设计，故只考虑受拉区受力。根据桥墩受力特点，桥墩横向拉应力在系梁对称轴剖面顶处值最大[4]。中心断面顶缘最大主拉应力为6.686 MPa，该处最大名义拉应力为6.653 MPa，向下逐渐减小，在距离顶缘0.646 m位置拉应力为0。墩顶沿x轴方向局部正应力云图如图5所示。

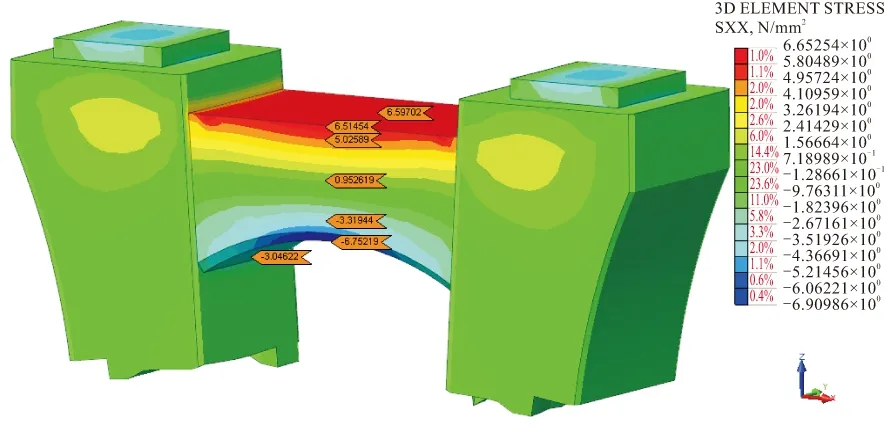
图5 墩顶局部正应力云图

墩顶系梁对称轴处墩顶至应力为0的各截面的横向正应力数据详见表1。

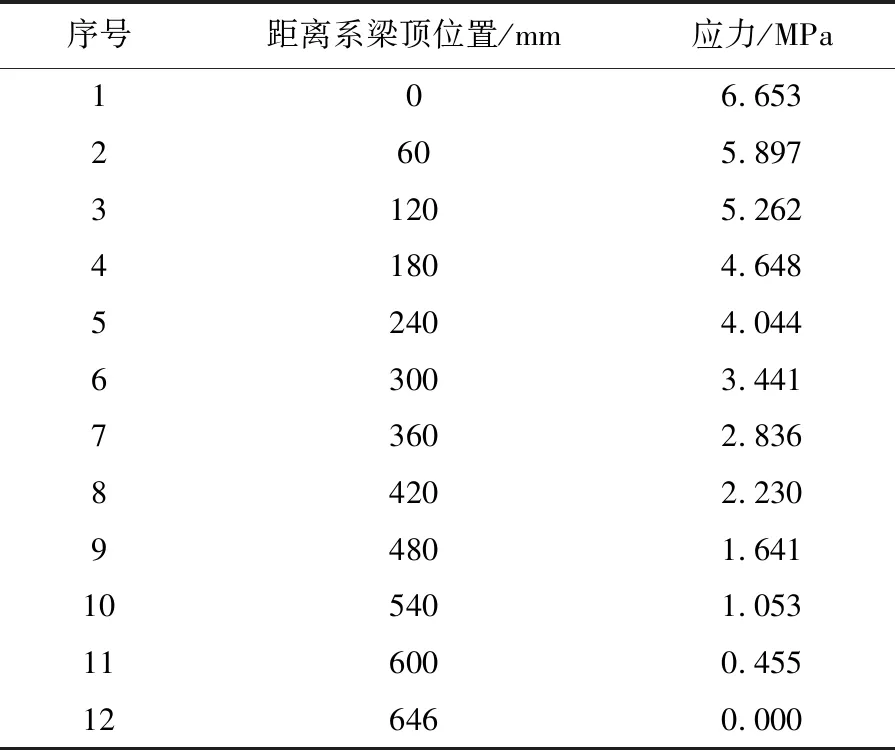
表1 墩顶系梁对称轴处横向正应力

从该截面的受力特点可以看出，距离系梁顶0.646 m范围内混凝土承受拉应力，其数值随距离墩顶高度的增加而减小；距离墩顶0.646～1.2 m范围内混凝土承受压应力，其数值随着距离系梁顶高度的增加而增大，最大压应力为6.733 MPa。

2.2.1 成桥状态下桥墩配筋验算

桥墩选取系梁对称轴处最不利的位置截面为典型局部构件进行配筋验算。

根据表1，绘制墩顶系梁对称轴处横向拉应力图，如图6所示。

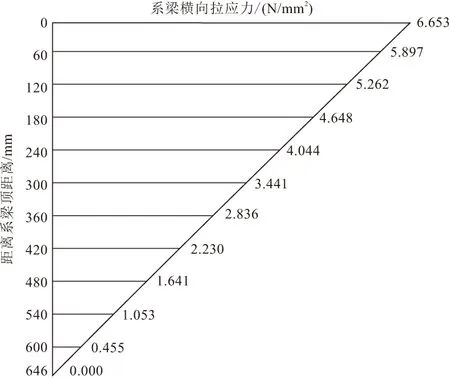
图6 系梁对称轴处横向拉应力

对该拉应力图进行积分，求得该系梁横向拉力值。Nd=A×b=2082.046×1800=3747682.8 N(A为应力图面积；b为系梁厚度)。通过配置钢筋来抵抗开裂，假设系梁横向拉力全部由钢筋来承担，将横向拉力除以钢筋控制应力(钢筋控制应力取180 MPa)，从而求得所需的钢筋面积As，As=3747682.8/180=20820.46 mm2，需配置34根直径28 mm的HRB400钢筋。

而系梁在该处截面主要抗拉的实际配置钢筋有46根直径28 mm的HRB400钢筋，将此钢筋建入模型，并假设钢筋和母单元之间是完全粘结没有滑移的，验算得到配筋后系梁顶混凝土最大名义拉应力为1.34 MPa，小于C40混凝土抗拉强度设计值1.65 MPa，故满足受力要求。

再根据花瓶墩顶“D区”[5]类似于“深梁”的受力特点，可考虑采用《规范》中的拉压杆模型来计算其系杆力作对比，根据以上实体计算所得的应力迹线，结合其受力变形图，按照杆件中心尽量与应力迹线重合的原则绘制杆件，建立的拉压杆模型如图7所示，在工程实例中，图中的压杆处有少数设置了撑梁[6]，但大多数考虑到桥下通车净空需求等原因不设置撑梁，此时压杆与传统意义上的压杆不同，其作用在混凝土外部，是“虚压杆”，压杆力仍难在此处存在，只是压杆力的平衡是通过墩柱抗弯来实现的[6]。据《规范》第8.4.7条规定，系梁顶部横向受拉用抗拉承载力公式考虑：γ0Tt,d≤fsdAs，Tt,d=0.45Fd(2s-b′)/h(式中:γ0为桥涵结构重要性系数；Tt,d为墩顶横向拉杆力内力设计值；fsd为普通钢筋抗拉强度设计值；As为拉杆中普通钢筋面积；Fd为墩顶竖向力设计值；s为双支座的中心距；b′为距离墩顶高度为h的位置处，墩帽的横向宽度；h为墩顶横向变宽度区段的高度)，其中，γ0=1.1，s=5500 mm，h=4000 mm，b′=6000 mm，fsd=330 MPa，可算出受拉钢筋面积需As≥27937.5 mm2，即需45根直径28 mm HRB400的钢筋。与以上实体有限元计算结果差异较大，此时拉压杆模型并不能准确计算双柱式花瓶墩的系杆力。另根据《规范》第6.4.3～5条进行裂缝宽度验算，而系梁该处截面主要抗拉的实际钢筋有46根直径28 mm的HRB400钢筋，将该系梁按偏心受拉构件考虑，根据以上条规中的公式Wcr=C1C2C3σss[(c+d)/(0.36+1.7ρte)]/Es(式中:C1为钢筋表面形状系数；C2为长期效应影响系数；C3为与构件受力性质有关的系数；σss为钢筋应力；c为最外排纵向受拉钢筋的混凝土保护层厚度；d为纵向受拉钢筋直径；ρte为纵向受拉钢筋的有效配筋率；Es为钢筋的弹性模量)，算得裂缝值为0.0976<0.2 mm，满足《规范》要求。

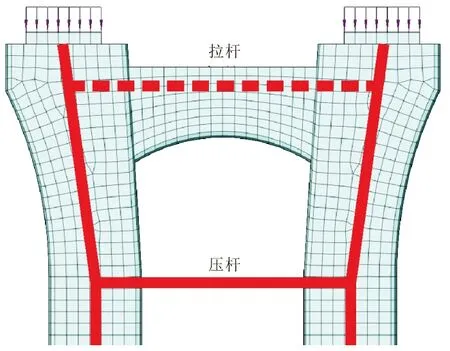
图7 拉-压杆模型

2.2.2 成桥状态下桥墩配筋验算结果

该桥墩墩顶实际设置了一层加强钢筋网，在单墩四周也设置了钢筋网，支座垫石设置了3层钢筋网以抵抗局部应力。经实体分析核算，在成桥状态，该桥墩各部位均满足受力要求，无开裂现象出现的可能。桥墩在成桥状态下受力分析结果表明：(1)《规范》中的拉压杆模型并不适用于其系梁拉杆力计算，可适用于独柱式花瓶墩计算[1,7,8]；(2)此时桥墩系梁的顶缘受拉应力，而底缘受压应力。

2.3 在墩顶顶升状态下桥墩受力分析

在以上桥墩的有限元模型中，建立局部实体单元模型模拟临时钢垫板，该模型尺寸为1.9 m(长)×0.35 m(宽)×0.8 m(高)，假设附加构件支座垫石不参与墩顶受力，但保留垫石与墩顶交叉单元面边线，用8节点六面体划分三维单元网格，建模时不考虑普通钢筋作用，模型共有实体单元29586个。卸载成桥状态下支座垫石上的荷载，同时在该临时钢垫板模拟单元上施加3D单元面法向面力，面压力P为16541353.38 N/m2(临时钢垫板支反力为11000 kN)。图8为墩顶顶升时有限元模型。

图8 墩顶顶升时有限元模型

从桥墩整体受力的主拉应力云图(图9)中能看出，随着墩顶作用荷载大小和位置的不同，与成桥状态对比，桥墩受力趋势发生较大的变化。墩顶系梁底部受拉而顶部受压，与成桥状态受力趋势相反。其对称轴截面底缘出现最大拉应力为4.526 MPa，向两边逐渐减小，而顶缘处压应力为3.992 MPa。

图9 顶升状态下墩顶局部正应力云图

在临时钢垫板下靠墩顶内侧下方出现的拉应力最大是在纵桥向，且在20 cm高度范围内的拉应力为0.486～0.711 MPa，将墩顶钢筋网及墩柱钢筋单元建入模型后计算，此处横桥向未出现拉应力，纵桥向最大拉应力为0.18 MPa，均小于C40混凝土抗拉强度的设计值1.65 MPa，故排除了文中开头描述的可能出现较大拉应力的情况，理论上不应出现裂缝。

将桥墩选取受力最不利的系梁对称轴处截面为典型截面进行配筋验算。现通过实体单元计算的应力进行积分求出截面内力，依据所得内力值进行配筋并验算。根据计算结果，墩顶系梁对称轴处各截面的横向正应力数据见表2。

由表2可知，距离系梁底0.542 m范围内混凝土承受拉应力，其数值随距离墩底高度的增加而减小，最大拉应力为4.217 MPa；距离墩底0.542～1.2 m范围内混凝土承受压应力，其数值随着距离系梁底高度的增加而增大，最大压应力为3.992 MPa。

2.3.1 顶升状态下桥墩配筋验算

桥墩选取系梁对称轴处最不利的位置截面为典型局部构件进行配筋验算。根据表2，绘制墩顶系梁对称轴处横向拉应力图，如图10所示。对该拉应力图进行积分，求得该系梁横向拉力值，Nd=A(应力图面积)×b(系梁厚度)=1058.95×1800=1906110 N。此时需要配置钢筋来抵抗开裂，假设系梁横向拉力全部由钢筋来承担，将横向拉力除以钢筋控制应力(钢筋控制应力取180 MPa)，从而求得所需的钢筋面积：As=1906110÷180=10589.5 mm2。需配置17根直径28 mm HRB400钢筋。

表2 墩顶系梁对称轴处横向正应力

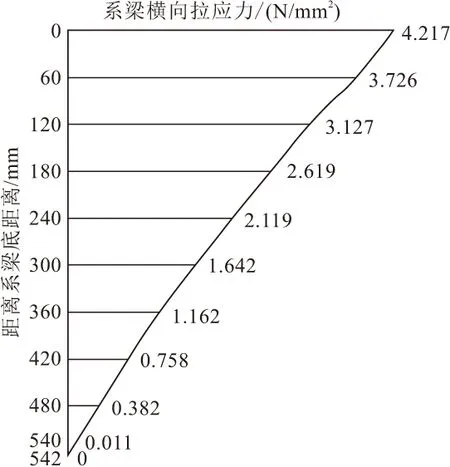
图10 顶升状态下系梁对称轴处横向拉应力

在此顶升状态时，桥墩受力趋势的变化较大，实际墩系梁顶受压，而底部受拉，与《规范》列出的各种拉压杆模型受力趋势不相符，故该《规范》算法也不适用于顶升状态时的双柱式花瓶墩系杆力的计算。

根据实体单元计算出系梁对称轴处的总拉力计算结果值，依据系梁底缘的实际配筋情况按偏心受拉构件模型进行裂缝验算。而系梁该处截面主要抗拉的实际钢筋有18根直径28 mm的HRB400钢筋，根据《规范》条规中的公式Wcr=C1C2C3σss[(c+d)/(0.36+1.7ρte)]/Es算得裂缝值为0.064<0.2 mm，满足《规范》要求。

2.3.2 顶升状态下桥墩配筋验算结果

根据以上在桥墩顶升状态时桥墩顶部的计算结果分析，临时钢垫板下墩顶内侧出现的裂缝，并非受到较大拉应力而引起的开裂。在墩顶顶升后，据现场仔细观察该桥墩系梁底也并未出现任何裂缝[9]，与本文中计算及验算结果相符。桥墩实际配筋情况均满足两种工况下的受力要求。

桥墩在顶升状态下受力分析结果表明：(1)在墩顶内侧设置临时钢垫板做支撑点对桥墩的受力改变较大，桥墩受力复杂，即便施工措施可以更加简单，但建议在条件允许的情况下尽量不在桥墩顶内侧顶升，以免改变构件受力后，某些部位配筋不足而引发安全隐患的可能；(2)顶升状态下桥墩系梁的顶缘受压而底缘受拉。

3 对施工中出现现象的处理措施

根据以上综合分析，桥墩在顶升过程中各结构均满足受力要求，理论上不应出现上述的开裂现象。据现场仔细观察发现，在施工过程中，由于临时钢垫板放在凹凸不平的墩顶表面，在钢垫板上施加荷载后，墩顶边上较突出的部分混凝土骨料承担了荷载，于是产生了较大的局部应力，再加上施工中局部混凝土净保护层不够，导致该处混凝土表层开裂。应将墩顶找平并抹一层水泥砂浆使钢垫板与墩顶表面充分均匀接触，故将该开裂的表层混凝土凿除后，按《规范》要求重新浇筑一层混凝土表层即可。

4 结 语

常用的双柱式花瓶墩墩顶受力类似于“深梁”，《规范》中的拉压杆模型难以准确计算其系梁的横向受力，而顶升状态时墩顶受力也不满足拉压杆模型条件，故该类型桥墩建议采用实体有限元等其它可靠的方法进行分析。

由于在墩顶处顶升主梁时对墩顶的受力影响较大，建议今后类似结构尽量避免在该处顶升，而采用其它更好的方法。

建议根据桥墩上部结构主梁的施工工艺情况，加强该类型桥墩系梁底部的钢筋配置，以便满足施工过程中的受力要求。