嵌岩钻埋式预制管桩基础受力机理
2021-01-05邹进涛李大海
彭 武,黄 天,邹进涛,李大海,方 晴
(1.黄冈强源电力设计有限公司,湖北 黄冈 438000;2.华中科技大学 土木与水利工程学院,湖北 武汉 430074;3.湖北省电力勘测设计院有限公司,湖北 武汉 430040)
输电线路工程沿山丘地区走线的趋势愈发明显,由于地形与复杂地质条件的制约,山区输电线路若采用常规的基础型式设计、施工往往受到多因素制约。比如挖孔桩基础人工挖孔施工效率低,孔下作业安全风险大;灌注桩基础机械钻孔采用的施工机具庞大,不方便转场,且施工道路修筑费用高。近来,一种新型微孔桩基础,如图1(图中l1为桩长)所示,采用微型预制管桩作为桩体,结合后注浆工艺,通过先钻孔(钻孔直径比管桩外径大100 mm)居中放置管桩,再在管桩桩侧注浆,将桩与浆液组合形成的锚固体与围岩紧密结合的方法,充分发挥钻孔桩和预制桩的优势,具有桩径小、所需作业面小、挖孔扭矩力小以及承载能力高的优点,适合在山区输电线路推广使用。而目前对该新型基础的设计主要是参照普通桩和嵌岩桩进行的。胡岱文等[1]通过对大量嵌岩桩原位测试桩数据的分析与研究,得出结论:嵌岩桩的承载力主要是由桩岩嵌固力来承担的;明可前[2]通过大量试验得出,当嵌岩深度为4倍桩径时,其承载力发挥最好;张建新等[3]提出,嵌岩桩单桩容许承载力的计算公式由嵌岩桩的桩土侧阻力、桩岩侧阻力以及桩端阻力三部分共同组成;刘洋[4]分析了嵌岩桩竖向承载力影响因素,认为分项综合设计法更符合嵌岩桩的承载力特点。
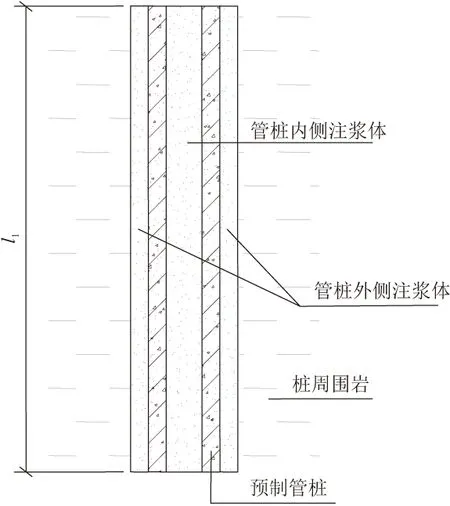
图1 钻埋式预制管桩
综上,嵌岩桩计算公式以经验和半经验公式为主,试验的普遍性较低,代表性不强,设计方法和参数取值也不尽相同[5~7],究其原因是缺乏对其受力机理的研究。
本文针对这种新型钻埋式预制管桩基础,采用荷载传递理论,借鉴已有岩石结构面剪切强度的方法,研究其受力机理,推导弹性和塑性破坏下桩身位移、侧阻力及轴向力随深度变化的解析式,以期为设计计算提供一些理论参考。
1 锚固变形受力研究
假定预制管桩与管桩外侧注浆体组成的锚固体与围岩之间的剪应力与剪切位移满足图2所示的本构关系[8,9],据此建立力学模型,并根据局部变形理论[10],推导锚固体受力平衡条件下的力学平衡微分方程,求解荷载传递的函数关系。
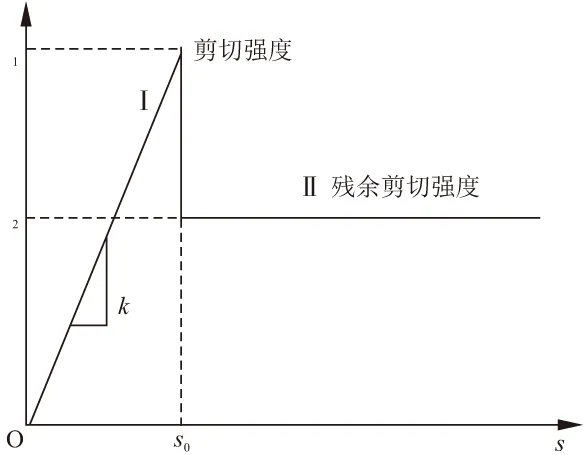
图2 锚固体-围岩界面剪应力本构模型
q=uτ(z)=kss(z)
(1)
(2)
式中:q为单元长度上的剪应力;u为锚固体周长;τ(z)为锚固体与围岩间的剪应力;s(z)为z处的位移;s0为锚固体弹性极限位移;ks为锚固体的剪切模量;τr为残余剪切强度。
张喜涛等[11]的研究表明,锚固体的剪切模量ks由围岩的剪切模量K1、管桩外注浆体的剪切模量K2和管桩的剪切模量K3组成,其表达式为:
(3)
根据锚固体-围岩界面(图3)的本构关系,锚固体弹性极限位移s1与锚固体-围岩界面极限黏结强度τ0相关,计算公式可简化为:
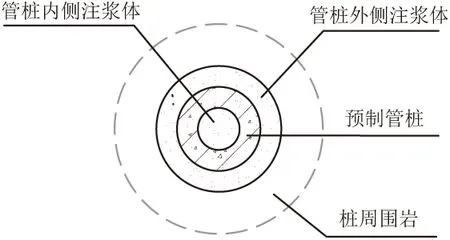
图3 锚固体-围岩截面
(4)
根据工程经验,锚固体-围岩界面极限黏结强度τ0可按表1选取[12]。

表1 水泥浆胶结注浆体同围岩间的黏结强度

表2 水泥浆胶结注浆体同混凝土的黏结强度[9]
通过对比表 1,2可以发现,注浆体与围岩之间的黏结强度远小于注浆体与混凝土之间的黏结强度,且现场试验发现,现场破坏一般发生于外侧注浆体与围岩界面上。
根据静力平衡条件:
(5)
联立式(1)(5)得到桩身轴力P(z)与桩侧剪应力的关系为:
dP(z)=uτ(z)dz
(6)
距锚固段始端间隔为z处围岩与锚固体的轴向应变εz和s(z)的关系为:
(7)
根据荷载传递理论,联立式(6)(7),对锚固体任一截面有:
(8)
Aa=Ab+Ag+Ac
(9)
EaAa=EbAb+EgAg
(10)
式中:Ab,Ag,Ac分别为管桩、管桩外注浆体和管桩内填充浆液的横截面面积;Eb,Eg分别为管桩、管桩外注浆体的弹性模量。
如图4所示,设作用于管桩顶部的荷载为Pd,相应的位移为sd,桩长为l1。在桩顶位移条件下,求解过程如下:
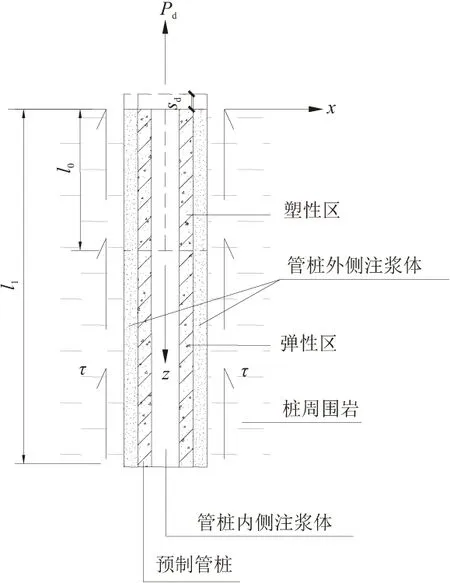
图4 桩侧摩阻力计算简图
(1)当桩顶作用荷载,围岩处于弹性状态(s(z)≤s0)时,将式(2)中τ(z)=ks(z)代入式(8),解得:
s(z)=C1eηz+C2e-ηz
(11)
(12)
式中:C1,C2为系数。
由轴力连续条件有:
(13)
解得:
(14)
(15)
(16)
(2)桩顶在荷载作用下,桩周上部塑性破坏,破坏区的深度为l1,Δs(z)>s0;下部处于弹性状态,其深度范围为l1~l1,此时Δs(z)≤s0。
根据锚固体-围岩界面本构关系,当作用在桩体与岩体界面上的剪应力超过界面极限黏结强度时,界面出现塑性破坏,会发生“脱黏”,脱黏段的剪应力即为界面残余强度,作用在脱黏段上的剪应力会重新分配和调整[14],如图5所示。
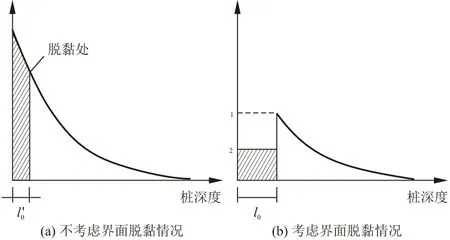
图5 桩侧剪应力沿桩体分布特征
由边界条件τ(z)|z=l′0=τ0,代入式(15)有:
(17)
解得名义脱黏长度l′0和实际脱黏长度l0:
(18)
(19)
根据何思明等[15]的研究,脱黏段的变形量可按下式计算:
(20)
所以:
(21)
1)在破坏区(s(z)>s0),将式τ(z)=τr代入式(8),解得:
(22)
式中:C3,C4为系数。
由边界条件:
(23)
可得:
(24)
(25)
(26)
Pl0=Pd-uτrl0
(27)
2)在弹性区(Δs(z)≤s0),将式τ(z)=ks(z)代入式(8)。
假定桩身轴力破坏区和弹性区的分界面上连续,有:
(28)
解得:
(29)
(30)
(31)
根据以上分析可知,作用在钻埋式预制管桩上荷载大小的不同,有两种侧阻力分布模式:
(1)当作用的荷载较小时,桩身处于弹性阶段,锚固体-围岩界面上的侧阻力按式(15)呈指数函数分布,侧阻力不超过锚固体-围岩界面极限黏结强度;
(2)当作用的荷载较大时,锚固体-围岩界面上的侧阻力分布为两段:桩身上部出现塑性区,此范围内锚固体-围岩界面上的剪应力超过界面极限黏结强度,锚固体-围岩界面会发生脱黏破坏,脱黏段的剪应力为界面残余强度;桩身下部处于弹性阶段,此范围内锚固体-围岩界面上的侧阻力按式(30)呈指数函数分布。
2 算 例
为验证本文提出模型的正确性,在此给出一个算例。
已知钻埋式预制管桩采用PHC200,桩径为0.2 m,管桩内外侧均采用高强水泥浆注浆,且外侧注浆层厚度为0.05 m,桩长为5.5 m,周围岩体为强风化片麻岩。计算所需的相关参数见表3。

表3 桩体参数
根据文献[11]的研究,围岩的剪切模量K1=5 GPa、管桩外注浆体的剪切模量K2=6 GPa、管桩的剪切模量K3=10 GPa。
图6为本文计算的桩顶位移和现场试验加载后桩顶位移分布曲线。从图中可以发现:本文计算结果和试验结果吻合良好;当桩顶上拔力不超过250 kN时,桩顶位移随上拔力线性增加,此时桩身处于弹性变化,当桩顶上拔力超过250 kN时,桩身出现塑性变形。
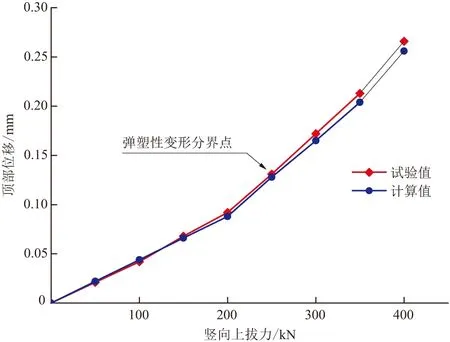
图6 理论计算和试验加载下的桩顶位移
图7~9分别给出了在不同上拔荷载作用下的桩身变形、桩侧剪应力、桩身轴力分布曲线。可以发现,当Pd=200 kN时,桩身处于弹性范围内,桩侧剪应力呈指数规律递减。当Pd=300 kN或Pd=400 kN时,桩身出现塑性脱黏区,且上拔荷载越大,脱黏区的范围也越大;塑性脱黏区的侧阻力为界面的残余强度,剪应力均匀分布,即150 kPa,弹性区域的剪应力呈指数规律递减。

图7 不同上拔荷载作用下桩身变形分布曲线
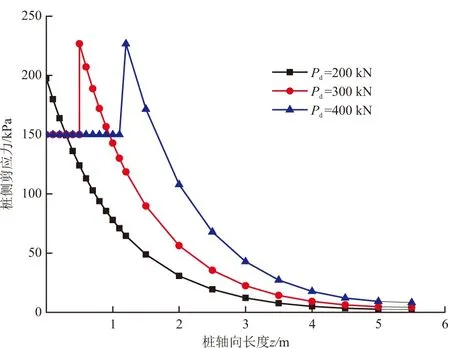
图8 不同上拔荷载作用下桩侧剪应力分布曲线
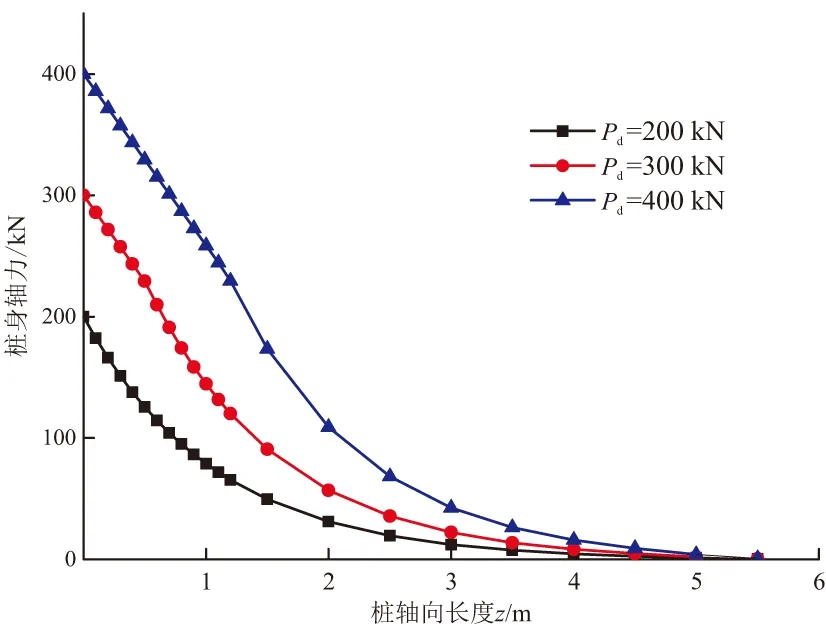
图9 不同上拔荷载作用下桩身轴力分布曲线
3 结 论
本文根据锚固体-围岩界面摩阻力分布规律,基于荷载传递理论,分析了钻埋式预制管桩与桩侧注浆形成的锚固体的受力机理,研究了锚固体在上拔荷载作用下桩身变形、桩侧阻力及桩身轴力的分布规律,得到以下结论:
(1)锚固体在上拔荷载作用下,锚固体-围岩界面分为弹性区和塑性脱黏区。
(2)当上拔荷载较小时,锚固体处于弹性区;当上拔荷载较大时,锚固体出现塑性脱黏区,且上拔荷载越大,塑性脱黏区的范围也越大。
(3)弹性区锚固体侧阻力呈指数规律递减,塑性脱黏区侧阻力均匀分布。
