中国汽车产业及其影响因素关系的研究—基于VAR模型的脉冲响应和方差分解

2021-01-05李洪庆王军雷康凯刘磊

汽车文摘 2021年1期

李洪庆王军雷康凯刘磊

（中国汽车技术研究中心有限公司，天津 300300）

主题词：汽车产业 VAR模型脉冲响应函数方差分解

1 引言

自1953 年中国第一汽车制造厂在长春开工建设以来，中国汽车产业走过了67年的历程，初步形成了大中小企业、主机厂和供应商、研发和生产销售3大联合体系。汽车产业是国民经济和社会发展重要的战略性、支柱性产业，也是制造强国建设重要的标志性产业，对带动产业结构调整、推动制造业转型升级发挥着重要作用。随着我国将汽车产业上升到国家战略层面，作为世界汽车产业的重要组成部分，汽车产业的发展关乎到经济的稳定和制造强国的建设。

近年来很多学者发表了一些关于汽车产业相关的研究：杨随[1]在对我国汽车产业生产布局深入研究后，发现随着省区专业化的不断提高，相对应的地理集中度呈现“扩散—集中—扩散”的趋势。王瑞晋等人[2]基于地理科学的基础理论，揭示了我国汽车产业布局的时空变化规律，分析了汽车产业发展现状，并提出相应的对策。贺灿飞等人[3]指出中国工业总体呈现“内陆—沿海—内陆”集聚特征，和改革开放以前相比，中国工业呈现出较为明显的聚集趋势。贺正楚[4]对我国2006～2015年31个省域汽车制造业进行研究，指出影响汽车制造业区域布局的主要因素有科技创新水平、劳动力成本、税收政策。巫细波[5]认为整车带动、政策引导、集聚经济、资源分布及空间成本等因素对汽车产业空间布局有重要影响。邓若冰等人[6]基于空间计量经济学的研究视角，探讨了我国2001～2003年省域汽车工业集聚和经济增长的空间关系。

从这些研究可以发现，学者主要是对汽车产业及其影响因素进行探讨，而对汽车产业与这些影响因素之间关系的探讨尚存在空白，在汽车产业发展的过程中，汽车产业的时序变化和社会经济、资源环境、生产研发能力等因素密切相关。基于以上考虑，以期作出以下2方面分析：一方面使用脉冲响应函数来研究汽车产量与其影响因素长期相互动态影响，另一方面运用方差分解研究汽车产量与其影响因素在相互冲击中的相对重要性。

2 数据说明和模型简介

2.1 VAR模型介绍

向量自回归模型（VAR）是自回归模型（AR）的拓展，1980年由Sims提出[7]，常用于预测相互联系的时间序列及分析随机扰动项对变量系统的动态影响。VAR 模型把每个内在变量看成是所有内在变量的滞后值的函数来构造模型，是基于数据的统计性质由多元时间序列变量组成的“向量”自回归模型。p阶VAR模型的数学表达形式记为VAR(p)，具体公式如下：

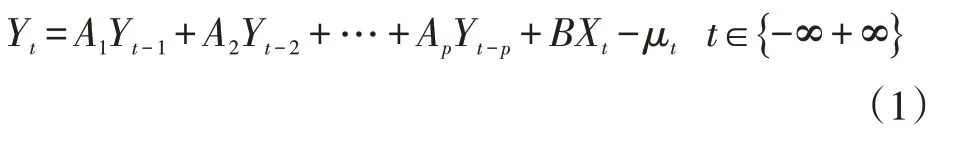
式中，Yt为k维内生变量向量；Xt为d维外生变量；μt是k维扰动向量；A1,A2，…，Ap和B是待估系数矩阵，p是滞后阶数。VAR模型转化为矩阵为：

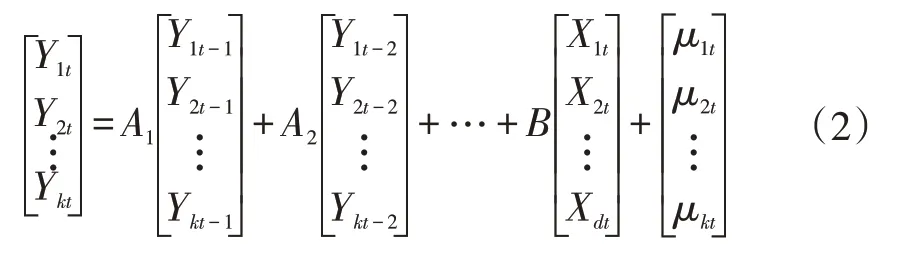
2.2 数据来源

论文中的研究数据主要从中国统计局和《中国汽车工业年鉴》[8]获取，根据确定的指标体系选择1983～2018 年中国汽车产量及其相关影响因素统计数据。以中国汽车生产数量作为因变量，用汽车产量（y）来表示。数据共涉及全国31 个省、市、自治区，由于制度差异，没有纳入分析香港、澳门和台湾3 个地区的数据。

2.3 指标体系构建

汽车产业是1个技术资金密集、关联波及范围广、带动能力强劲的支柱产业。本文以汽车生产水平作为被解释变量，用汽车产量来表示。在选择解释变量时，借鉴了国内外学者关于时空演变的研究成果。同时又针对中国的具体情况，从社会经济、资源环境、生产研发能力3个方面构建了中国汽车生产时序变化的计量经济模型（表1）。此外，中国汽车生产还受到政策因素的影响，由于政策因素在VAR模型中无法有效量化，运算过程中会产生虚拟变量，影响模型准确性，所以本文选取具有政策意义的汽车行业完成固定投资代替。

表1 时间序列影响因素指标体系

居民消费水平（x1）

居民消费水平和国民生产总值（GDP）、居民储蓄和居民人均收入等多个经济因素息息相关，能够很好地反映居民整体消费能力，具有极为重要的社会经济意义。故本文引入居民消费水平来分析其对中国汽车生产的影响。

汽车工业总产值（x2）

汽车工业总产值是衡量汽车工业发达程度和规模总量的重要指标。工业总产值的计算价格有2种：一是不变价格，另一个是现行价格，由于本文研究跨度36年，所以如果采用不变价格会影响模型精准性，故本文所有数据采用的均是现行价格。

汽车进口数量（x3）

中国汽车进口数量从1983 年的2.24 万辆到2018年的113万辆，增长50.4倍，汽车进口数量的逐年增加会冲击本地汽车的生产。本文把汽车进口数量引入到影响因素的分析中。

汽车行业完成固定资产投资（x4）

汽车行业固定资产投资是指在一定时期内建造和购置固定资产的工作量以及与此有关的费用变化情况，从固定资产投资角度可以来探讨汽车行业宏观经济走势及行业政策方向。所以本文将把汽车行业完成固定资产投资纳入指标体系。

工程技术人员数（x5）

汽车产业是技术人才密集型行业，行业的整体进步需要人才的积累和技术水平的提高，而且工程技术人员还关乎着企业的创新成果转化。因此本文引入工程技术人员来分析对中国汽车生产的影响。

全员劳动生产率（x6）

全员劳动生产率可以衡量劳动力要素的投入产出效率，是劳动力积极性、企业管理水平、生产技术水平的综合体现，是考核企业和行业的重要经济指标。故本文把全员劳动生产率引入到影响因素的分析中。

3 实证分析与估计结果

3.1 平稳性检验

建立VAR模型的基础是验证变量是平稳的，否则会出现伪回归现象，即建立的回归模型在经济意义上没有因果关系。本文采用单位根检验方法（ADF）验证时间序列的平稳性。为了保证回归参数估计量具有良好的统计性质，消除异方差，对居民消费水平、汽车工业总产值、汽车进口数量、汽车行业完成固定资产投资、工程技术人员、全员劳动生产率和汽车产量分别取对数为lnx1，lnx2，lnx3，lnx4，lnx5，lnx6，lny，结果显示7个变量均为非平稳序列，因此对变量进行一阶差分，结果显示序列平稳，数据水平为一阶单整，记为D(lnx1)，D(lnx2)，D(lnx3)，D(lnx4)，D(lnx5)，D(lnx6)，D(lny)。检验结果如表2所示。

3.2 滞后阶数的确定

一般情况下，解释变量和被解释变量的因果关系不会在同一时期发生，通常会有时间滞后性，所以模型滞后阶数（Lag）的确定对模型的可靠性和准确性十分关键。结合表3可以看出：除了施瓦兹准则（SC）准则显示最后滞后阶数为1，似然比检验（LR）、最后预测误差（FRE）、赤池信息准则（AIC）、HQ 信息准则均显示最优滞后阶数为2，故本文选取滞后2 期为最优滞后阶数。

3.3 格兰杰因果检验

格兰杰因果关系是为了检验时间序列变量之间在统计上的时间先后顺序，即x的前期变化能否有效地解释y的变化，如果x的前期变化能有效地解释y的变化，即认为x是y的格兰杰原因，相反，不是y的格兰杰原因，选取滞后2期作为最优滞后期。

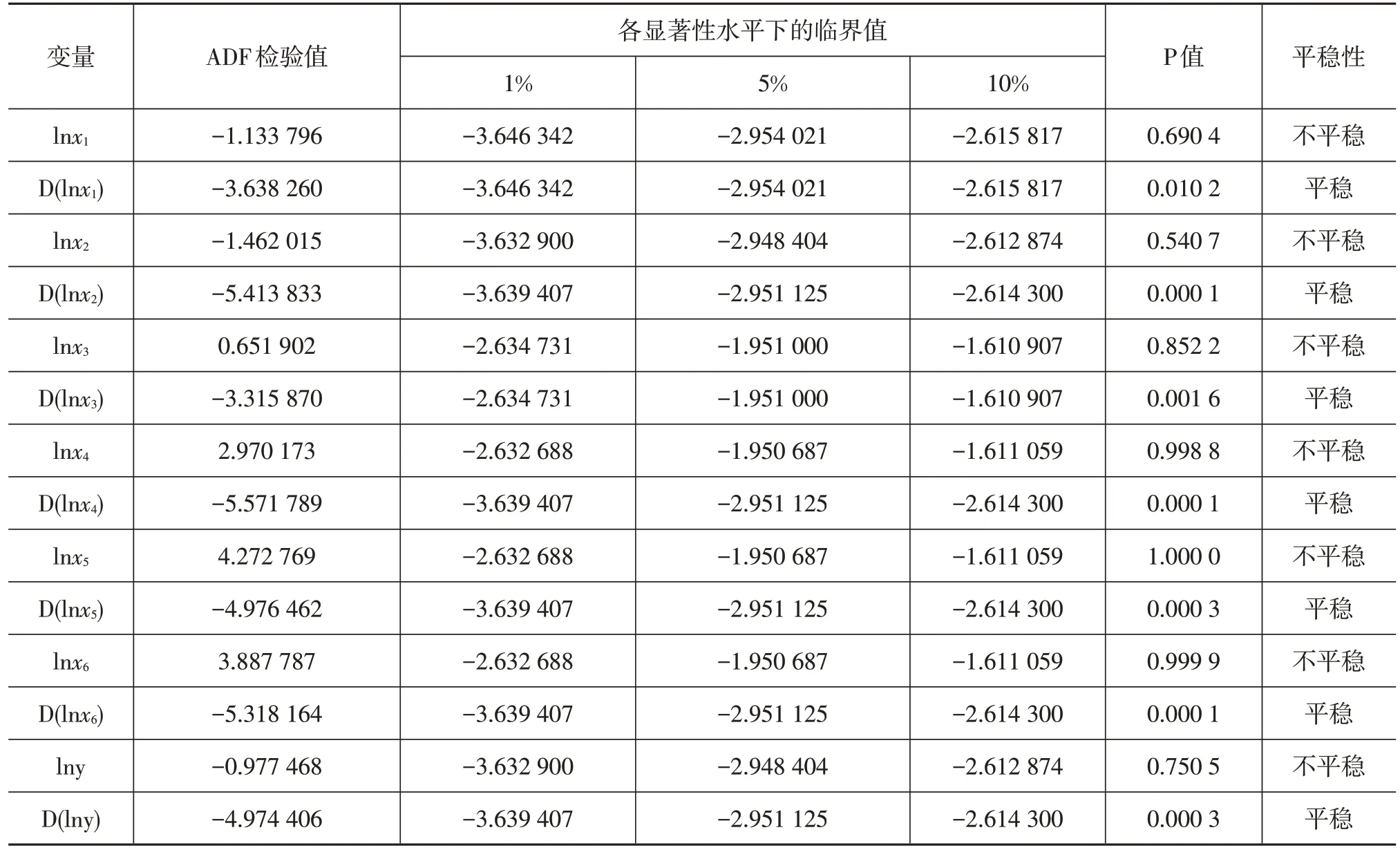
表2 变量的平稳性检验结果

表3 VAR模型滞后期选择标准

由表4 可以得出，居民消费水平（x1）是汽车产量变化的格兰杰原因，说明随着居民生活水平的提高，人们对于汽车产品的需求逐渐增强，同时汽车产量变化也对居民生活水平有显著影响；汽车工业总产值（x2）不是汽车产量变化的格兰杰原因，即当年汽车工业总产值的滞后作用对汽车产量变化无显著影响；汽车进口数量（x3）不是汽车产量变化的格兰杰原因，然而汽车产量变化是汽车进口数量的格兰杰原因；汽车行业固定资产投资（x4）对汽车产量变化的影响较小；同样，工程技术人员数（x5）也不是汽车产量变化的格兰杰原因；全员劳动生产率（x6）是汽车产量变化的格兰杰原因，说明企业劳动力积极性、企业管理水平、生产技术水平的提高可以显著影响汽车产量的变化；汽车工业总产值、汽车进口数量、汽车行业固定资产投资、工程技术人员数分析结果虽然不是汽车产量变化的格兰杰原因，但是他们可以影响汽车产量的变化，只是影响程度较小，下面将用脉冲响应函数、方差分解来分析这些变量之间更为复杂的关系。

表4 格兰杰因果检验结果

3.4 VAR模型稳定性检验

在进行脉冲响应分析与方差分解分析之前必须对VAR 模型进行稳定性检验，一般采用使用AR根图表(AR Roots Table／Graph)，如果模型所有根的模数都在单位圆内，说明模型是稳定的，否则不稳定。由图1可知本文被估计模型有部分模数在单位圆边缘，较难判断其模数是否小于1，所以采用AR 根图和AR 根表结合来分析。

图1 VAR模型稳定性检验

从图1 和表5 可以看出，被估计模型所有模数都位于单位圆内，说明所建立的VAR 模型是稳定的，可以继续进行脉冲响应分析与方差分解分析。

表5 VAR模型稳定性检验

3.5 脉冲响应函数

脉冲响应函数主要用于研究动态系统内变量之间的关系，它是1种因果性分析方法[9]。具体来说，脉冲响应函数是用来衡量随机扰动项的1 个标准差冲击对变量系统的动态影响，能够清晰直观的刻画出变量之间的相互关系，横坐标表示冲击作用的滞后期数，纵坐标表示汽车产量的响应程度，选择分析期长度为10期，实线表示脉冲响应函数计算值，上下的虚线为正负2 倍标准差置信带。脉冲响应函数分析结果如图2所示。

从图2（a）可以看出，当本期给居民消费水平1个正向冲击后，居民消费水平的冲击会对汽车产量带来负面影响。当冲击后在第2期内影响最大，后逐渐减弱，在第8期达到第二次影响峰值。看似这一结论不符合实际，但是仔细思考可以看出，当在一定时间段内居民消费水平过度提高时，会在一定程度上透支消费者的需求，比如2009年的《汽车行业调整振兴规划》即汽车下乡政策公布后，迅速释放消费者需求，导致在2011 年和2012 出现汽车销量增长疲软，所以产量相对减少也在情理之中。

图2（b）显示，对汽车工业总产值1 个正冲击后，会给汽车产量带来正面影响，在第4期达到最大，随后影响逐渐减弱。这是因为汽车产业是1 个长期性产业，作为产业革命的核心，它具有相当长的产业链，包括上游的钢铁、玻璃等，中游的整车制造，以及下游的汽车销售及服务等。当本期的汽车工业总产值达到一定值，在一定程度上反应了汽车行业全产业链的快速发展，自然会带动汽车产量的增长。

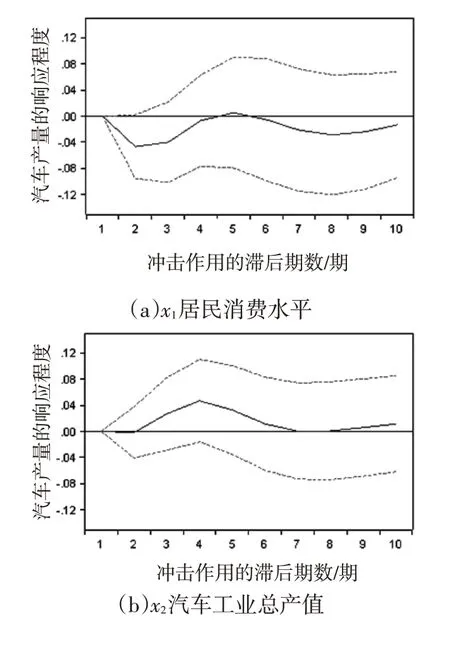
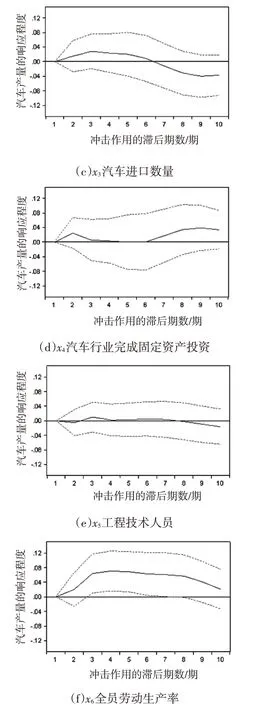
图2 各自变量冲击对汽车产量的脉冲响应函数（实线表示脉冲响应函数计算值，上下虚线为正负2倍标准差置信带）

图2（c）表明，汽车进口数量在前6期对汽车产量是正向影响，这是因为汽车进口数量的增长反映出汽车市场需求的增加，第6期后产生负向效应，是由于汽车进口市场的繁荣在一定程度上影响了国内汽车市场。

从图2（d）个图可见，汽车行业固定资产情况的冲击对汽车产量有正向的影响，在第2期影响最大，后逐渐减弱，从第7期后开始重新增强，并趋向平稳。这是由于随着汽车行业固定资产的增加，体现出国家及地方政府对汽车行业的支持，目前我国31个省市区中，有28个省区把汽车产业确立为支柱产业。

图2（e）表明，工程技术人员数的正向冲击对汽车产量的影响力较弱，这和中国汽车销量主要由市场需求带动有分不开的关系。

从图2（f）可知，给全员劳动生产率1 个标准差大小的冲击后，汽车产量有显著正向影响，在第4期达到最大，后缓慢趋于平稳。随着劳动生产率的逐渐提高，汽车行业整体生产效率稳步提升。

3.6 方差分解

脉冲响应函数主要用来衡量每1个变量产生的冲击是如何影响另1个变量的，方差分解是脉冲响应分析的重要补充手段，可以进一步分析影响内生变量的结构冲击的贡献度。对解释变量和被解释变量进行方差分解，研究各变量的贡献度，选择分析期长度为10期，图3为VAR模型方差分解图，其中横纵坐标分别表示滞后期数和解释变量对汽车产量变化的方差贡献率。

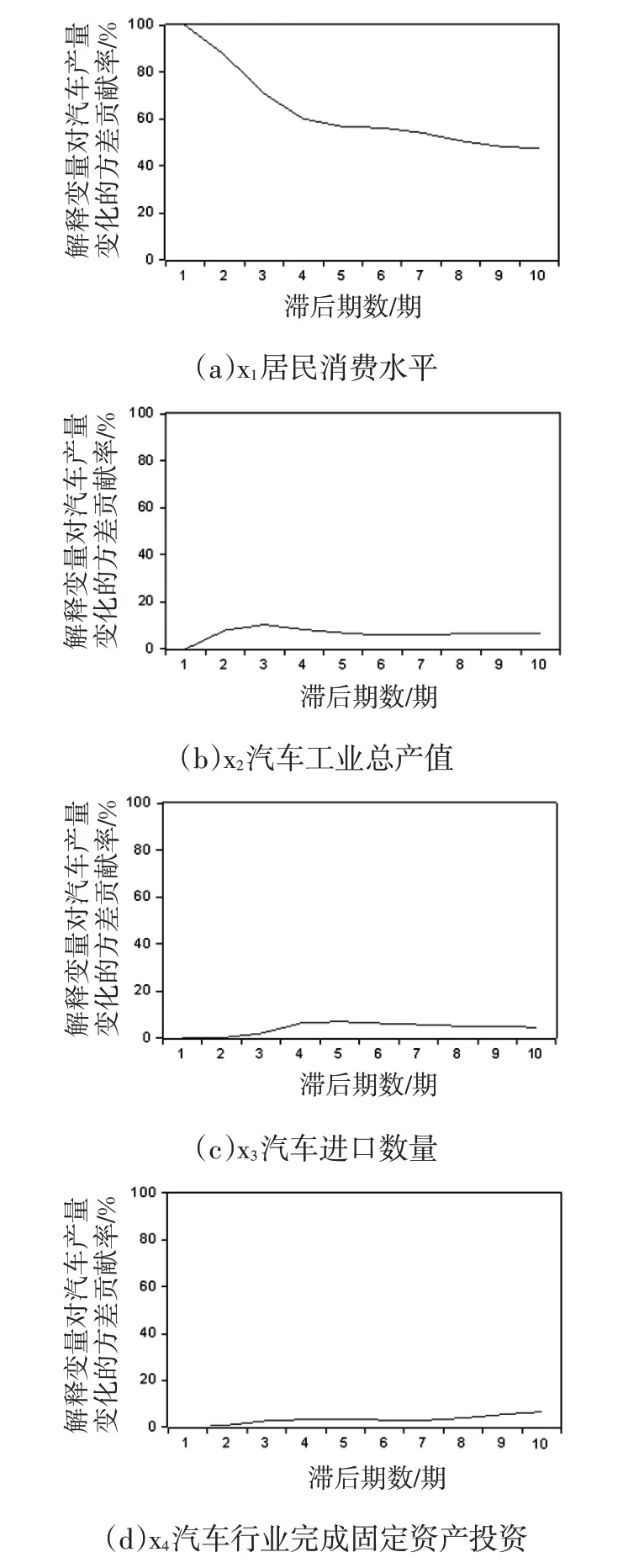
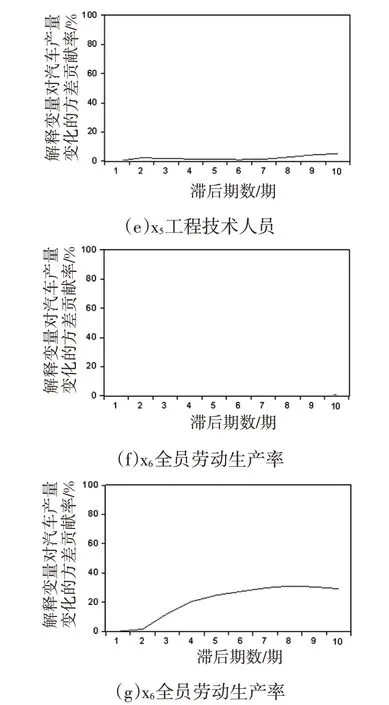
图3 VAR模型方差分解

从图3可以看出，汽车产量变化从第1期到第4期对自身的方差贡献率由100%降到了60%，后逐渐缓慢下降。全员劳动生产率从第1期的0逐渐上升，在第8期达到最大值31%，后趋于稳定，工程技术人员贡献率一直在0附近，其它变量贡献率为6%左右。由此可见，汽车产量自身的变化对汽车生产影响程度最大，其次为全员劳动生产率，然后依次为汽车进口数量、居民消费水平、汽车行业固定资产投资、汽车工业总产值、工程技术人员数。