一种抑制单相电网直流偏置的新型锁相环

辛志远，黄晓辉

（1.中国核工业电机运行技术开发有限公司，北京 100043；2.南京赫曦电气有限公司，江苏南京 211100）

0 引言

随着化石燃料等不可再生能源的减少以及人们环保意识的增强，可再生能源（如太阳能、风能等）也获得了更加广泛的应用和发展[1]。锁相环（Phase-Locked Loop，PLL）是实现电网同步以及单相并网系统闭环控制的关键。锁相环能否准确检测相位角以及频率将直接影响电能质量及其单相并网系统的可靠性[2]。

如何解决锁相环输入中存在的直流偏置是一个具有挑战性的问题。直流偏置会导致所估计的基频相位偏差和频率振荡[3]。直流偏置产生的方式有多种，如：电压传感器测量误差[4]，A/D 信号处理环节引入[5]，以及电网故障[6]。直流偏置在逆变器电压中产生的误差，违反了标准IEEE 1547—2003 和IEC61727 的要求[7-8]。为了解决直流偏置带来的不良影响，许多学者已经提出了几种解决方案：在文献[9]中，采用线性小信号状态空间模型分析了直流偏置对基于常规同步参考坐标系（Synchronous Reference Frame，SRF）的锁相环产生的影响进行了定量分析。给出了SRF-PLL 固有的带宽与直流偏置变化的关系。随着输入直流偏置的增大，所提出的方案的带宽必须相应的减小，然而这大大的影响了动态性能。文献[10]通过延迟的方法提取了输入信号和α 轴输出信号之间误差，得到一个分量，然后经过一个积分器进行处理，最后从输入信号中减去估计出的直流分量。文献[11]提出了一种控制同步d 轴电压的直流偏置误差为零的补偿算法。首先利用积分器估计直流偏置误差，然后通过调整PI 控制器来消除直流偏置。这种方法的稳态和瞬态响应良好，计算量小。但是，其硬件要求高。文献[12]提出了一种基于二阶广义积分器（Cascade Generalized Integrators，CGI）的固定频率的级联型锁相环来抑制输入的直流偏置。第一个二阶广义积分器（Second Order Generalized Integrator，SOGI）的α 轴输出作为第二个SOGI 块的输入。第二个SOGI 块的αβ 轴输出作为嵌入式SRF-PLL 的输入。然而，SRF-PLL 的带宽会影响动态响应以及其谐波抑制能力。在文献[13]中，提出了一种改进的SOGI 锁相环，通过在正交信号发生器（Orthogonal Signal Generator，QSG）中加入第三个积分器及其输出来消除输入的直流分量。它可以在不增加系统复杂性的情况下提高性能，但在实际应用中必须提供输入信号的基频和相序，这大大限制了其应用。

为解决上述问题，本文保留了传统二阶广义积分器的优点，针对其不可以抑制直流分量的缺点，结合全通滤波器，提出了一种新方法。本文首先论述了SOGI 锁相环法的基本原理，阐述了其在抑制直流偏置方面的局限性，然后提出了ESOGI（Enhanced SOGI）改进算法，并给出了实验结果。

1 基于二阶广义积分器的传统锁相环

1.1 正交信号的生成

与三相电网环境不同，在单相电网环境下由于相间电压缺失现象，无法直接通过Clark 变换构造正交向量，多数情况下借助正交信号发生器构建所需的标准正交信号ugα和ugβ。静止的α-β 坐标系的方法主要有移相（延时）法、数字积分法、数字微分法等[14]。但由于移相（延时）法不具有抑制谐波能力，传统的基于Hibert 变换及基于Park 变换的正交信号生成方法的结构复杂，数字化实现困难。而二阶广义积分与以上两种方法相比，不仅具有谐波抑制能力，而且易于实现，得到学者越来越多的重视。

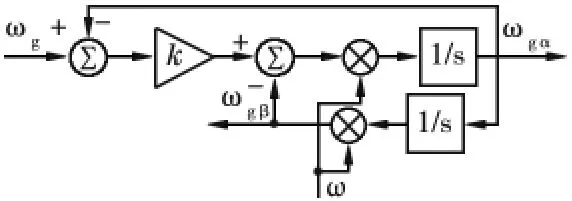
图1 传统二阶广义积分结构

根据图1，可以得到二阶广义积分在s 域的闭环传递函数为：

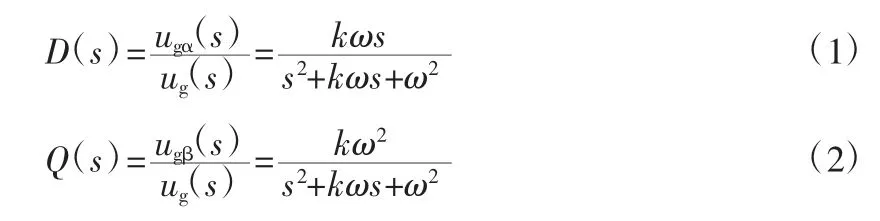
当k=1、ω=100π 时，可得二阶广义积分器（SOGI）的波特（bode）图（图2）。

从图2 的波特图可以看出，经过D（s）处理后，输入的50 Hz 的交流信号会产生90°的滞后相移，且其幅值不会产生改变，但是对于直流分量无衰减作用；而Q（s）具有带通滤波特性，在50 Hz 谐振处信号幅值不变，并且对低频分量与高频分量的信号具都有衰减作用。

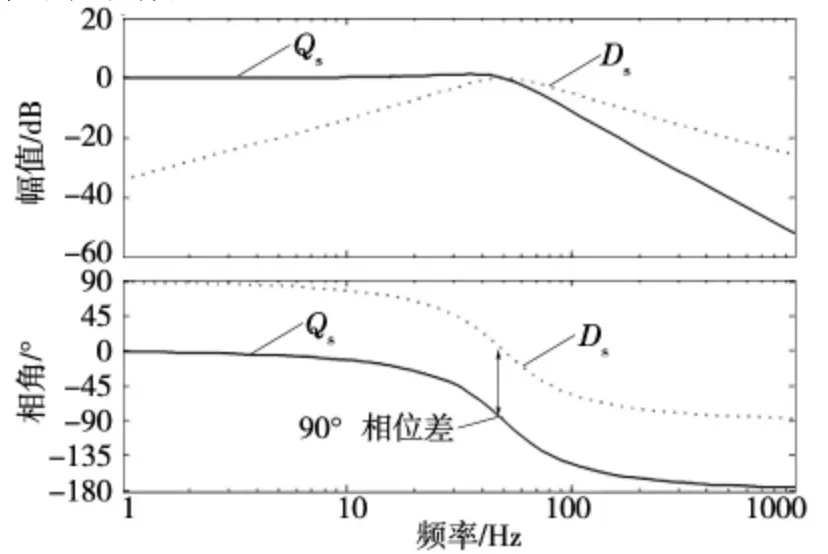
图2 基于SOGI 的正交信号生成波特图

1.2 单相锁相环原理

基于同步参考帧的锁相环如图3 所示。uα和uβ为通过坐标变换产生的两个正交信号，可以描述为:

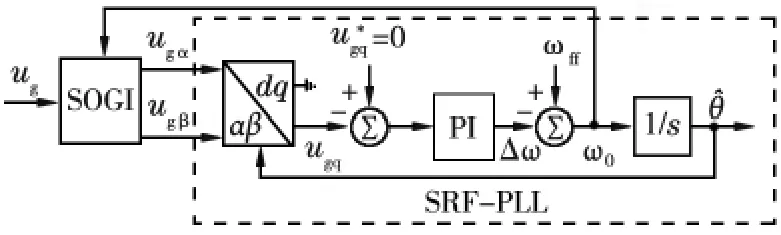
图3 基于同步参考帧的单相锁相环结构示意

其中，Um为电网电压的幅值，θ 为电网的相位。θ 可以表示为θ=ωgt+φ，其中ωg和φ 分别为电网电压的初始角频率和相位。

Park 变换（αβ→dq）可以定义为：

图3 中，ωff为前馈电网角频率，在本文中通过赋值使其等于电网角频率，即100π rad/s（50 Hz）。假设相位角和频率估计正确，传统单相锁相环的输出正是电网电压的基波分量。但是实际电网中存在的直流分量，相位突变以及谐波分量往往对锁相环产生不良影响。其中，由于直流分量的低频性，往往更难得到有效抑制。

1.3 直流偏移的影响

直流偏移存在于输入信号中，可能是由于系统临时故障测量以及转换过程的结构和限制而产生的。输入信号中存在直流偏置分量，可能导致锁相环估计的相位和频率的基频产生误差。

由图2 可知，在二阶广义积分器中D（s）具有带通作用可以消除输入信号中的低频和高频分量，然而Q（s）具有低通作用，无法消除输入信号中的直流分量。因此，当输入电压包含直流分量时，α 轴和β 轴电压可以表示为：

其中，Udc代表输入电压中包含的直流分量。通过同步参考系变化，d 轴和q 轴电压可以表示为：

d 轴和q 轴电压通过化简可以表示为：

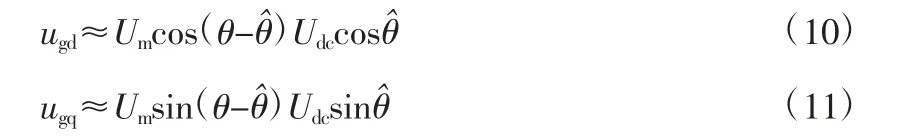
从式（10）和式（11）可知，当相位误差足够小的时候，同步d轴电压和同步q 轴电压具有相同的频率分量。从图3 可知，q 轴电压作为SRF-PLL 的输入，q 轴电压的畸变导致锁相环系统中电网相位和电网频率的畸变。本文将直流偏置抑制作为主要目标，以减小估计的电网相位和电网频率的畸变。

2 改进型单相锁相环

为避免电网电流直流分量对谐波电流检测的影响，必须对单相电网电流的直流分量进行抑制。图4 为增强型二阶广义积分器的结构图，该结构在二阶广义积分的基础上，增添了一个全通滤波环节，以达到滤除直流分量的目的。

图4 中，ugα、ugβ与输入ug的关系可由式（1）与式（2）表示，而去除直流分量后的输出信号ug0与输入信号ug的关系可表示为:

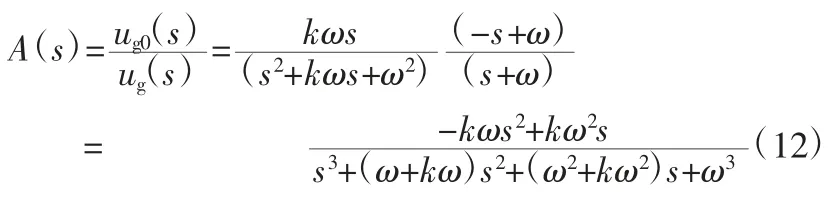
根据式（10），取k=1，当ω=100π 时，可得到波特图（图5）。

由图2 的波特图可知，D（s）对信号的带通作用，对直流分量有天然的滤除作用，而正交分量ugβ需滤除其直流分量。由图5 可知，改进后的A（s）既能满足对信号产生相位差90°的要求，又具有带通作用，可以滤除直流分量。

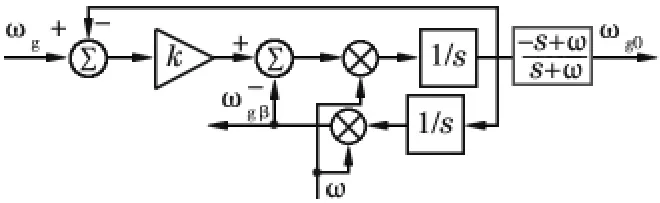
图4 增强二阶广义积分结构

传递函数中k的取值不同，传递函数的带宽也会发生变化。如果k 值增大，传递函数的滤波效果会更好，但对动态响应的时间也会随之增加。从而选择合理的k 值滤波效果和动态响应时间这两个因素之间的权衡，在本文取中k=1。

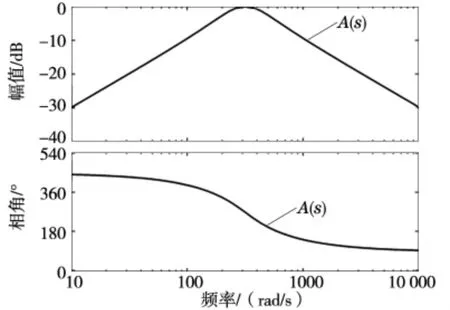
图5 基于增强型SOGI 的正交信号生成波特图

3 SOGI 的离散化

为了方便数字控制，需要实现传递函数的离散化。以式（1）和式（2）为例，选择双线性变换方法进行离散化，因为前向欧拉法和后向欧拉法在50 Hz 下无法提供准确的90°相位差。

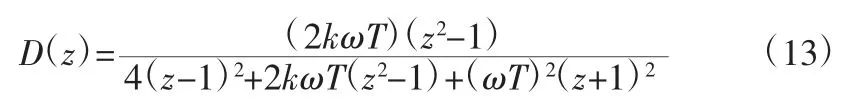
其中，T 是采样时间，k 是阻尼系数。经过化简可得D（n）：

其中，x 和y 为系统的输入和输出信号，n-1 和n-2 分别表示前一时刻和前两时刻的采样结果。参数a0、a1和b0可以写为：

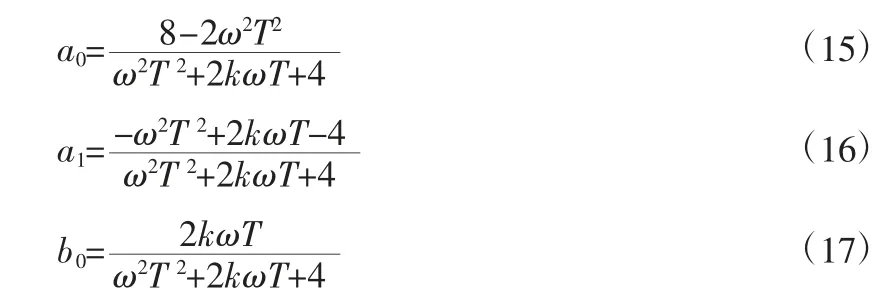
同理，Q（n）可以表示为：

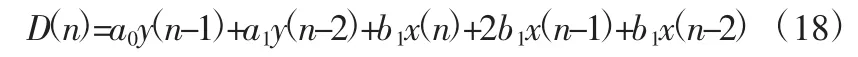
4 实验验证

本节研究在DSP（Digital Signal Processing，数字信号处理）环境下进行，对SOGI-PLL 和ESOGI-PLL 的性能进行了有效评估。在整个仿真过程中，采样频率固定在20 kHz，电网频率设置为50 Hz。本文设计了3 个测试实验。

实验l：电网电压相位跳变+90°。

实验2：电网电压含有20 V 的直流分量。

实验3：电网电压含有10%谐波分量。

霍尔电压传感器测量单相电网电压，然后通过内部ADC（Analog-to-Digital Converter，模数转换器）将检测到的模拟信号发送给DSP。经过DSP 处理后，通过DAC（Digital-to-Analog Converter，数模转换器）模块输出实验结果。

图6 展示了在实验1 所模拟的条件下，SOGI-PLL 和ESOGI-PLL 的实验波形对比。在开关点时刻，输入电压发生10%直流偏移的变化。由于输入信号添加直流偏置，这导致在SOGI-PLL 输出的uβ包含直流偏置信号。此时锁相环输出的追踪信号也将产生误差。在输入信号含有相同直流偏置条件下，ESOGI 的实验波形见图6b）。然而，由ESOGI 生成的ugα和ugβ为无偏置的正弦波和余弦波，表明输入直流偏置已被ESOGI 结构消除。

图7 展示了实验2 所模拟的条件下，SOGI-PLL 和ESOGI-PLL 的实验对比结果。图中可以清楚地看到，当电网电压ug在开关点处发生突变时（相位跳变45°），ESOGI-PLL 完成锁相的稳定时间远小于SOGI-PLL。SOGIPLL 大约需要15 ms（图7a）中的t1），而ESOGI-PLL 只需要7 ms（图7b）中的t2）。从以上实验结果可以看出，ESOGI-PLL 的动态响应时间比SOGI-PLL 短得多。因此，ESOGI-PLL 能够更快地完成相位的追踪。

图8 为实验3 所模拟的条件下SOGI-PLL 与ESOGIPLL 的实验对比结果。从开关点开始，输入电压受到谐波分量的污染，总谐波失真（Total Harmonic Distortion，THD）为10%。可以看出，SOGI-PLL 和所提出的ESOGIPLL 都具有抑制谐波分量的能力，而改进后的SOGI 能保持低通滤波特性和带通滤波特性，所以足以消除直流偏置以及电网电压谐波的不利影响。

由以上实验结果可以看出，即使是相角跳变、直流偏置或谐波分量，它们对ESOGI-PLL 输出结果的影响也很小。

图6 电网电压包含直流分量时的实验结果

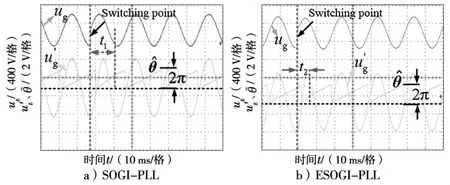
图7 电网电压发生相角跳变时的实验结果

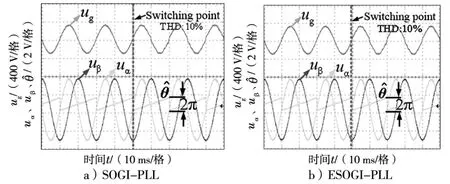
图8 电网电压包含谐波时的实验结果

5 结论

针对传统的锁相环无法消除输入端直流电压偏移的现状，本文提出了一种基于SOGI 和全通滤波器的单相锁相环。首先分析了传统锁相环以及改进型锁相环的传递函数，揭示了直流偏置产生影响的机理。然后，在电网电压发生畸变的条件下，进行了实验验证和比较。可以得出结论，即使在直流偏置、相位突变以及谐波分量影响的情况下，ESOGI-PLL 也能够很好的锁定电网相位。此外，由于结构简单，所提出的ESOGI-PLL 可以很容易地在微控制器中实现。