网络Meta分析研究进展系列（二）：网络Meta分析统计模型及模型拟合软件选择

张天嵩，孙凤，董圣杰，杨智荣，武珊珊，田金徽

Meta分析可以定量、科学地整合研究结果，已在许多科学领域取得显著成果[1]，在医学领域中常可用于比较不同干预措施有益还是有害。在临床中，针对同一种疾病常存在多种干预措施，医师决策时需根据所有可获得的证据对不同干预措施进行全面比较，但在实际情况下，干预措施的疗效间往往缺乏可靠证据或尚无直接比较证据，该问题可能需要通过两种途径解决：一是开展同时评估多种干预措施利弊的随机对照临床试验，但存在诸多困难，可行性较差；二是通过网络Meta分析（network meta-analyses，NMA）在一个证据体中同时评估多个干预措施，通过合成直接和间接比较的证据，可获得证据体中任一对比较的干预措施之间更为精确的相对效应估计，并根据测量结局（如有效性和安全性）的优劣进行排序[2]，由于NMA的上述优势，越来越多方法学团队聚焦于直接和间接证据整合理论和方法，自Lumley[3]提出NMA的概念及Meta回归分析策略以来，基于不同的学术观点，已有多个研究团队提出各自的NMA模型和分析策略，如贝叶斯分层模型、频率学方法、图论法等[4]，并可由诸多强力软件实现[5]，如WinBUGS、R、Stata、SAS、Stan等。本文通过文献梳理NMA相关理论进展，对NMA统计模型、建模策略、分析策略和统计软件进行总结，并给出选择建议和注意事项。

1 建模数据

1.1 观测数据和缺失数据大多数NMA统计模型（如经典Lu & Ades模型[6]），均以观测到的数据（observed data）建模；而Zhang等[7]认为，一般情况下，纳入NMA中的每个研究只是对所有干预措施中感兴趣的子集（如2个或3个干预措施）进行比较，因此表示成为典型“研究×干预措施”矩阵的数据结构非常稀疏，并以一项NMA研究[8]为例说明这一问题。该研究共纳入117个随机对照研究来比较12种新型抗抑郁药物的疗效，其中114个是两臂研究，3个是三臂研究，很显然是具有显著缺失的不完全块结构数据。如果忽略了非完全随机产生的缺失数据，仅依赖观测到或未观测到的数据信息，则估计会产生偏倚[9]。Zhang等建议可以从不完全数据中获得附加信息，把研究中未观测到的臂作为缺失数据，然后借用其他研究中观测到的相关信息，基于马尔可夫链蒙特卡洛（Markov chain Monte Carlo，MCMC）算法填补，从而建立了一种新的缺失数据框架建模方法[7,9]。

1.2 数据类型与效应尺度选择与经典Meta分析相同[10]，根据测量结局的不同，NMA的数据类型一般也分为二分类数据（dichotomous data）、连续型数据（continuous data）、有序数据（ordinal data）、计数数据（count data）和时间事件数据（time-to-event data）等五大类。二分类数据是NMA中最常用的数据类型，一项调查研究表明[11]，共纳入186个NMA研究，其中测量结局数据类型报告为二分类数据者111个（60%）、连续型数据者53个（28%）、时间事件数据者17个（9%）、有序数据者5个（3%）；二分类数据效应量选择比值比（odds ratio，OR）者66个（35%）、危险比（risk ratio，RR）者44个（23%）、危险差（risk difference，RD）者0个（0%）、同时报告OR、RR、RD者1个（1%），连续型数据效应量选择均数差（mean difference，MD）者43个（23%）、标化均数差（standardized mean difference，SMD）者9个（5%）、均数比（ratio of means，RoM）者1个（1%），时间事件数据效应量选择风险比（hazard ratio，HR）者17个（9%），计数数据效应量选择率比（rate ratio，RR）者5个（3%）。

目前尚无明确的选择效应量的理论原则可供参考。一般认为，根据不同测量结局数据类型，从可解释性和数学特性等角度考虑，选择合适的效应尺度[11]。以二分类数据为例，因OR具有良好的数据特性，Coory等[13]推荐在间接比较中选择使用OR，一些学者则推荐使用RR[14]，Caldwell[11]则认为OR有时会因呈现大的效应量出现错误解释，建议采用HR（如果事件时间研究的结果是二分类数据，也可由四格表计算出HR）。

建议在进行NMA时，可以基于各种因素合理选择效应量：①测量结局数据类型；②干预效应的可交换性及可加性，在进行Meta分析时，效应尺度假设观测到的干预效应是线性可加并假设在研究间是可交换的[15]；③科学依据，如有时获益危险比（RRb）和损害危险比（RRh）可能提供不同量级和方向的结果[11]，再如在合并不同基线风险的研究时，选择RR、OR和RD等不同效应量可能会影响干预排序等[16]；④直接比较的研究间异质性，如RD比RR、OR更容易出现异质性等；⑤必要时可选择不同效应量，作为敏感性分析。

1.3 数据格式NMA中待分析的数据，按格式一般分为标准化数据（normalized data）和非标准化数据（non-normalized data）两种，适用于不同建模模型和拟合模型软件要求。前者又称为长数据或窄数据，是每个研究中每个臂占一行，主要变量有研究名称、每个臂发生事件人数和总人数；后者称为短数据或宽数据，是每个研究占一行，主要变量有研究名称、所有干预措施的事件发生数和总人数。

因为NMA部分相关术语没有完全统一，为了便于后续讨论，在此我们介绍和区别几个术语：①干预（treatment）和臂（arm）：前者是指待评估的药物或医疗设备，而后者是指关于单个研究中被随机分配到的药物或医疗设备的患者资料（组）。②参照干预（reference treatment）和基线干预（baseline treatment）：前者是指标准对照干预如安慰剂，可用于与其他阳性干预进行比较；后者是指在每个研究中被指定为对照臂的干预。两者在大多数情况下相同，但也可能不同。③设计（design）：是仅指某试验中相比较干预措施组合，如Hasselblad[17]研究分析过的“AHCPR Smoking Cessation Guideline Panel”戒烟数据中共含有24个研究，有“未干预（No intervention）”、“自助（Self-help）”、“个体辅导（Individual counselling）”、“小组辅导（Group counselling）”等四种干预措施，假设分别以A、B、C、D表示，则Gritz 1992研究中含有干预措施A、B，则称为AB设计；Cottraux 1983研究中含有干预措施A、C、D，则称为ACD设计，依次类推，该概念在设计×干预交互模型（designby-treatment interaction model）中非常重要。

2 统计模型

2.1 基本原理假设NMA中共含有S个研究，T个干预措施，N个直接配对比较，干预措施k相对于干预措施c（中k,c=1,2,…,T）的相对效应为μck，实际上并不需要计算所有μck，只需要估计部分基本参数即可，基本参数μt（t=1,2,…,T-1）表示（-1）个相互独立的合并干预效应。简单方法，通过选择T个干预措施中某一个为参照（如A），则每个μt代表干预措施t相对于A（t=1,2,…,T；t≠A），所以，NMA需要估计所有μtS，因此，所有其他比较（功能参数）的合并效应则可以通过一致性等式μck=μAk-μAc=μk-μc获得。

2.2 主要的统计模型简单的网络结构为由A、B、C三个干预措施构成的星形结构，假设有“A vs. C”和“B vs. C”直接比较的证据，则可以通过校正间接比较（adjusted indirect comparison，AIC）方法按NMA一致性等式获得“A vs. B”的证据，即是最初用NMA统计分析的Bucher法。后来逐渐发展起来并在当前最为流行的NMA数据统计分析模型如层次模型、多元Meta分析模型、Meta回归模型、两步策略线性模型等都是基于NMA基本原理中一致性等式，最小化需要待估计的参数数量，虽然模型各异，实质上是等效的[18]，基本上是广义线性模型的拓展，没有优劣之分。在实际中，应根据软件实现模型的能力及研究者专业知识和技能来选择的相应的模型，基于此，本文主要介绍两种最为流行的结构模型（structural models）：层次模型和多元Meta分析模型。

2.2.1 层次模型层次模型（hierarchical models）是NMA最常用的数据分析模型[11,18]，由Lu与Ades[6]、Salanti[19]、Dias[20]等提出并不断完善，建模灵活、易于扩展，是目前众多贝叶斯NMA的基础，核心为广义线性模型（generalized linear model，GLM），可以通过不同的连接函数拟合服从二项分布、正态分布、泊松分布等指数分布的数据。英国国家健康与临床研究所（National institute for health and clinical excellence，NICE）决策支持机构（Decision Support Unit，DSU）制作的技术支持文档（Technical Support Documents，TSDs）中提供了层次模型针对不同数据类型的贝叶斯NMA代码，有兴趣的读者可以从DSU官网（nicedsu.org.uk）上下载学习。

设有N（i=1,2,...,N）个研究，每个研究有k（k=1,2,...,K）个干预措施（臂），第i个研究中的干预措施组合为Di（即是前文所谓的设计），第i个研究第k个臂中感兴趣的参数为ηik，该参数可由不同度量模型（measurement model）用来描述数据，对于二类数据，以pik表示第i个研究第k个干预措施组事件发生概率，总人数ηik，发生的事件人数为rik，rik服从二项分布：rik～Binomial（pik,nik），而概率。

层次模型有两种建模策略，第一种为Ades、Salanti、Dias等提出的基于对比（contrastbased）模型[21-23]，指定每个研究中的臂bi作为基线参照，则有nik=μibi+δibik（k=Di）。式中μibi称为研究截距，是固定效应，针对二分类数据表示第i个研究中臂bi的发生事件（戒烟数据中戒烟成功）比数的自然对数。δibik表示第i个研究中臂k（k=Di）相对于bi比较的特定比较效应，相应为比数比的自然对数（lnOR），当k=bi时，δibik=0；若k≠bi，则随机效应模型为模型中μ1k关键参数，表示如果以干预措施1为参照干预，对于k＞1（表示在1之后）的臂k与1比较的平均干预效应，显然μ11=0。若为固定效应模型，则有δibik=μbik=μk=μbi。

A systematic literature search was conducted using Pubmed and EMBASE with the terms of “complete mesocolic excision”, ”CME”, “anatomy of CME”, “laparoscopic CME” as well as “colon surgery”. Many related studies were found and we summarized and presented the findings with our clinical experience.

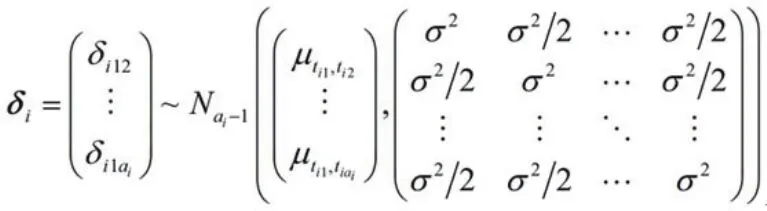
式中ai（ai=2,3…）表示第i研究的臂的数，μti1tik=μ1tik-μ1ti1；由δi的方差-协方差矩阵可知，对于任意两个臂之间的协方差为σ2/2。根据多元正态分布的条件分布公式可得每一个δi,1k条件分布为：

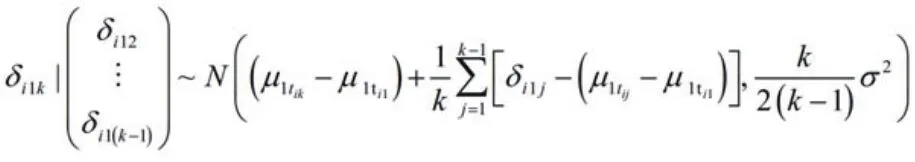
第二种为Hong[9]、Hawkins等[23]提出的基于臂（arm-based）建模策略。仍假设有N（i=1,2,...,N）个研究，每个研究有k（k=1,2,...,K）个干预措施（臂），第i个研究中臂的总数为K，s[k]表示研究中臂k，t[k]表示该臂施加给患者的干预措施，dt表示干预措施t相对于参照干预（t=1）的干预效应，显然有d1=0，臂k事件发生数与未发生数的比值对数为ηk，μs[k]表示参照干预的研究特定测量结果，根据异质性假设不同可分为固定效应模型和随机效应模型[23]：一是，假定不同随机效应方差发生个体干预措施水平则为具有干预措施特定方差随机效应模型（Random treatment effects with treatment-specific variance），ηk=μs[k]+δs[k],t[k]，式中；二是，假定所有比较间随机效应方差相同，则为共方差随机干预效应模型（random treatment effects with common variance），ηk=μs[k]+δs[k],t[k]，式中；二是，如果研究间无异质性，则为固定效应模型ηk=μs[k]+dt[k]。

2.2.2 多元Meta分析模型多元Meta分析模型（multivariate meta-analysis model）由White等[25]在Salanti等工作基础上提出，假设整个网络中含有T个干预措施，研究i均为两臂研究，其观察效应为yi，设T-1个基本参数μt表示tA间比较的效应，为每个研究中的系列子集，随机项为δi，随机误差为εi；如果某些研究中不含参照干预措施A，可采用数据填补技术给予臂A一个极小的数据信息，NMA中所有比较均可通过基本对比来表达，每个研究中报告一个或多个测量结局yitA=yit，则一致性模型为。该模型适合任意测量结局，如MD、SMD、lnRR、lnOR等。可以看出，对于比较组不含臂A的研究，通过数据填补变为至少含有三臂的研究，因此在每个研究中不同干预措施间的满足方差－协方差的多元正态分布[26]。

设计×干预交互模型基于本模型发展而来[25,27]，衍生出固定效应和随机效应不一致性模型等。仍假设某NMA网络含有T个干预措施A，B，C等等，令A作为共同参照，首先，假设纳入Meta分析的研究中均含有A（对于不含臂A的研究，可通过数据填补）；令d=1，2……，D表示设计类型，假设在第d个设计（d=1至D）第i个试验（i=1至nd）中，干预措施J（J=B，C，……）与A比较的结果为可表示任一测量结局，如MD，SMD，logRR，logOR等等，则不一致性模型为[28]：

模型中，δAJ表示J与A间对比的总效应，可视为固定参数，为感兴趣的参数。表示异质性，是指同一设计真实治疗效应的变异，一般视其为随机效应该模型对Σ无约束，作为非结构化模型，在模型中，J-A对比研究间方差为K-J对比（J，K≠A）研究间方差为不同对比研究间方差确实各异。对于Σ还存在两种可能的结构化异质性模型，在全结构化异质性模型中，假设所有干预对比有相同的研究间方差τ2，考虑J-A对比研究间方差，对于所有J允许ΣJJ=τ2，考虑K-J对比研究间方差，同样允许ΣJK=τ2/2（J≠K），因此有Σ=τ2P(0.5)，此处P(ρ)为矩阵，其对角元素等于1，远离对角元素等于项表示设计间不一致性，一般作为固定效应处理[25]，也可以作为随机效应模型处理[28]，假定ωd： ～Nc(0,Σω)，式中Σω为矩形矩阵，其对角线数值为对角线外其他数据为在一致性模型中，设表示研究内误差，假设εdi：N(0,Sdi)，而假定Sdi已知。

NMA中同质性假设和一致性假设是两个非常重要的假设。基于同质性假设衍生出固定效应模型（fixed-effect model）和随机效应模型（random-effects model），基于一致性假设衍生出一致性模型（consistency model）和不一致性模型（inconsistency model），这些不同的模型体现在结构模型中，在实际应用中，可以结合数据特点、模型特点及拟合数据的不同模型拟合优度来选择。

2.3 建模策略虽然NMA统计模型有多种，但建模策略即是NMA的度量模型（measurement model）分为两种：基于臂（arm-based，AB）和基于对比（contrast-based，CB），为了避免引起术语混淆，本文采用AB似然和CB似然，两者的主要区别有：①两者假设不同，Shuster[29]介绍了Meta分析中研究随机（studies at random，SR）和效应随机（effects at random，ER）两种随机效应方式，前者假设纳入Meta分析中的每个研究是独立的，后者假定每个研究的效应是随机的。CB似然需要ER类假设，而AB需要SR类假设[7]。②两者估计方法不同，CB似然采用近似正态来产生每一相对干预合并效应量及其方差；而AB似然则可直接对每个臂的绝对效应如ln（odds）建模[30]。③AB似然处理随机干预效应为臂水平治疗反应的变异[23]。

3 分析策略

贝叶斯统计学与经典统计学是统计学两个主要学派，两者对概率定义有所区别，而NMA也主要有贝叶斯和频率学两大分析策略。

3.1 贝叶斯分析框架贝叶斯统计综合了未知参数的总体信息、样本信息及先验信息，根据贝叶斯定理，获得未知参数的后验分布，进而对未知参数进行统计推断，因其灵活性强，广泛应用于科学研究中。贝叶斯NMA全面考虑了参数的不确定性，可以用直接概率来描述这些参数（如，一种干预措施优于另一种干预措施的概率）。贝叶斯NMA中主要采用MCMC和集成嵌套拉普拉斯近似（integrated nested Laplace approximations，INLA）两种算法，在使用MCMC算法时要注意几个主要问题[2]：

一是对模型中的参数合理指定先验分布。先验分布可以允许利用先验信息确定，但在先验信息或知识缺乏的情况下，常用的处理方法[31,32]：对绝对或相对效应测量（位置参数）选择指定无信息或模糊正态先验分布；根据测量结局类型，对研究间异质性标准差τ（尺度参数）指定为弱信息通常是均匀先验分布。在NMA文献中[32]，无论是固定效应模型还是随机效应模型，对所有研究中每个干预效应（如μib）和基本参数（如假定以A为参照，dAB,dAC,K）通常指定的先验分布为正态分布Normal(0,103～5)；对于随机效应模型中，研究间异质性标准差τ的先验分布指定为均匀分布uniform(0,2～10)，如果配对比较的研究稀疏，则可以指定半正态分布HN（0.5）或HN（1）[33]。二是若在后验分布中使用马尔科夫蒙特卡罗链模拟，则判断检验马尔科夫链收敛十分重要；需要指出的是，与MCMC算法相比，INLA算法费时短且不需要收敛性诊断。三是通常使用偏差信息准则（Deviance information criterion，DIC）对模型进行比较并评估其拟合度，公式为：DIC=pD+D-，式中，pD又称为参数的有效数量，D-用于测量模型复杂程度， 用于测量模型的拟合优度，由偏差D(θ)度量。DIC值越小说明模型越好，一般认为不同模型的DIC的差值在3个或以上单位即为重要差异[2,20]。四是贝叶斯模型因其复杂性和指定先验分布潜在的主观性，可能会影响到研究的结果。

3.2 频率学分析框架频率学分析框架广泛应用经典Meta分析中，但近年来涌现出的Meta回归及多元Meta分析等NMA模型和方法等，均可由频率学分析框架实现，且具有计算速度快、不需要为参数指定先验、可避免蒙特卡洛误差分析、可由Stata、R、SAS等通用软件轻松实现等优点，也得到广泛应用[2,26]。在NMA中，频率学分析方法的估计和推断常是基于最大似然（maximum likelihood）等算法[21]。频率学分析框架是观察数据在假设参数值的样本分布下的概率，得到的参数估计比贝叶斯方法更间接[34]。

因为NMA许多技术及相关统计软件，最初建立和开发时均基于贝叶斯方法，当前大多数NMA文献都是采用贝叶斯分析框架；同时，相对于频率学方法，贝叶斯方法在处理复杂或稀疏数据时更有价值[34]，因此，在NMA的数据分析时，建议首选贝叶斯方法，以频率学方法作为敏感性分析，但对于非统计学专业研究者而言可能会存在不少困难。

4 统计软件

可实NMA的软件或程序大体可以分为三类：一是，贝叶斯统计分析软件，如WinBUGS、OpenBUGS、JAGS、Stan等，可以实现贝叶斯NMA；二是，通用分析软件，如Stata、R、SAS等，既可以实现贝叶斯NMA，也可以实现频率学NMA；三是NMA专用分析包或程序，如ADDIS、GeMTC 、ITC、某些Excel插件如NetmetaXL和MetaXL等。决定进行NMA后，需要根据数据类型、效应量、证据类型等情况确定合适的统计模型和分析框架，然后再选择合适的计算软件，具体如表1所示[2,26]。

根据建模数据、软件功能特点及易用性等方面考虑，建议WinBUGS、Stata、R等三个主要NMA软件两两配合使用或三者联用：

（1）WinBUGS是NMA中最为常用的软件包[34,35]，但对于初学者而言，学习和理解其模型代码是一个挑战，且该软件在数年操作、数据注释和绘图制图等方面的功能有所欠缺[35]。建议使用JAGS，它是一个采用MCMC算法拟合贝叶斯层次模型的程序，与BUGS语言同源，但与OpenBUGS和WinBUGS有些小差异，并可由其他软件如R调用。

（2）Stata软件的mvmeta命令和network组命令均可拟合多元Meta分析模型[2,26]，其中mvmeta功能强大，但在数据预处理、模型参数设置、结果图示化等方面，需要一定的数学及统计学技能，初学者不易掌握；network组命令提供了数据准备、数据分析、绘制相关图形、干预措施效果排序等功能，特别是最新版本可通过调用mvmeta命令或WinBUGS软件等实现频率学及贝叶斯NMA，分别拟合，操作方便，建议使用network组命令。这两个命令均可在联网情况下，在Stata命令输入窗口键入命令：net from http://www.homepages.ucl.ac.uk/～rmjwiww/stata/，按提示完成安装，具体使用方法，可以阅读相关文献[2,26,36]。

（3）R软件除了有通过调用WinBUGS（如R2WinBUGS）、OpenBUGS软件（R2OpenBUGS、BRugs、rbugs）、JAGS软件（如R2jags、rjags、runjags）、Stan软件（如rstan）进行NMA的扩展包外，还有gemtc、pcnetmeta、bnma、netmeta等几个NMA专用包。gemtc包基于层次模型、采用对比似然建模策略，但因检查出的错误未及时修改而于2020年5月28日从R综合档案网络（comprehensive R Archive Network,CRAN）镜像仓库中移除。pcnetmeta包是基于臂建模策略[36]，通过调用JAGS软件，可以对二分类数据、连续型数据、计数数据等不同数据类型进行NMA，如针对二分类数据，可以计算绝对风险（absolute risk，AR）、RD、lnOR、lnRR、OR、RR等效应量，指定Probit连接函数建模[37,38]。bnma包用于拟合Dias[20]提出的层次模型，基于对比策略建模，通过调用JAGS软件进行NMA，但不需要用户编写JAGS代码和设定初始值等，使用方便。

表1 网络Meta分析模型及常用实现软件

5 结语

本文针对典型数据的NMA主流统计模型进行了梳理和介绍，并给出相关的选择和使用建议，不正之处，敬请斧正。NMA作为一种新技术和方法发展迅速，在实施时会面临着更多的挑战，一些重要问题尚未完美解决，如，NMA满足同质性、相似性（可传递性）、一致性等假设的证明问题；效应调节因子影响干预效应大小、干预措施疗效排序等问题。总之，NMA可以对多个干预措施的有效性和安全性等进行比较，是一种具有广阔前景的技术和方法，但研究者在应用时也必须注意其不足之处。