重庆兴隆隧道在流固耦合作用下围岩稳定性研究

王 锋，张雨浓，朱宝强，侯云乾，李志军，刘春树，王述红

(1.中交隧道工程局有限公司， 北京 100020；2.东北大学 资源与土木工程学院， 辽宁 沈阳 110819)

随着我国社会经济发展进入的一个新的历史性的阶段，我国的交通运输业也将进入一个新的发展时期。在我国除西北地区，每年的年降水量为400 mm～1 600 mm之间，地下水水位较高且地下水极为丰富，隧道的软岩通常是处于富水状态，在“山城”重庆极为明显。在隧道的修建及运营过程中，因为其地质的复杂性及不确定性，施工过程中的涌水以及运营过程中水的渗流造成的围岩损伤，是隧道需要解决的安全问题。富水地层隧道承受的主要是地层压力和水荷载[1]。尽管隧道设置排水沟，但是在排水装置下，由于应力场-渗流场耦合作用的影响以及对于围岩及支护结构的共同承载作用，在任何一种排水方式下，支护结构上的荷载确定是很困难的，对需要考虑水压力的隧道，除了考虑作用在结构上的围岩压力外，还需要考虑静水压力和围岩传导过来的渗透体积力[2]。对于渗透体积力可分为水势梯度成比例的渗透动压力和与体积成比例的浮力[3-5]。郭鸿雁等[6]以某富水隧道为依托,借助FLAC3D软件通过流固耦合数值分析了围岩无注浆条件下隧道外水压力随排水量的变化规律,进而提出了基于结构安全的隧道外水压力取值和地下水排放标准；李明等[7]根据室内土工试验数据,建立三维有限元模型,基于流固耦合和不耦合效应,分析对比了富水大断面黄土隧道采用CRD法和双侧壁导坑法施工时的初期支护受力和变形特征、地表沉降及孔隙水压力场分布特征；徐建国等[8]研究了不同围岩等级、埋深条件下,考虑流固耦合效应时,隧道开挖后围岩渗流场、应力场、位移场及塑性区的分布特征,探讨了流固耦合效应对围岩稳定性的影响。与非耦合条件下计算结果的对比分析表明,流固耦合效应对开挖后的围岩稳定性具有较显著的影响。陈明奎[9]以某下穿库区铁路隧道为依托工程,对比分析有无渗流场作用和不同水深条件下,隧道结构应力变化规律以及围岩变形、塑性区和渗流场的变化特性,同时还考虑隧道加固圈厚度和渗透系数对围岩稳定性的影响。 本文以重庆兴隆隧道为例，对围岩的稳定性进行流固耦合研究。

1 工程概况

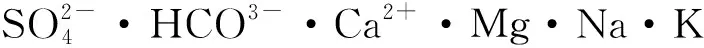
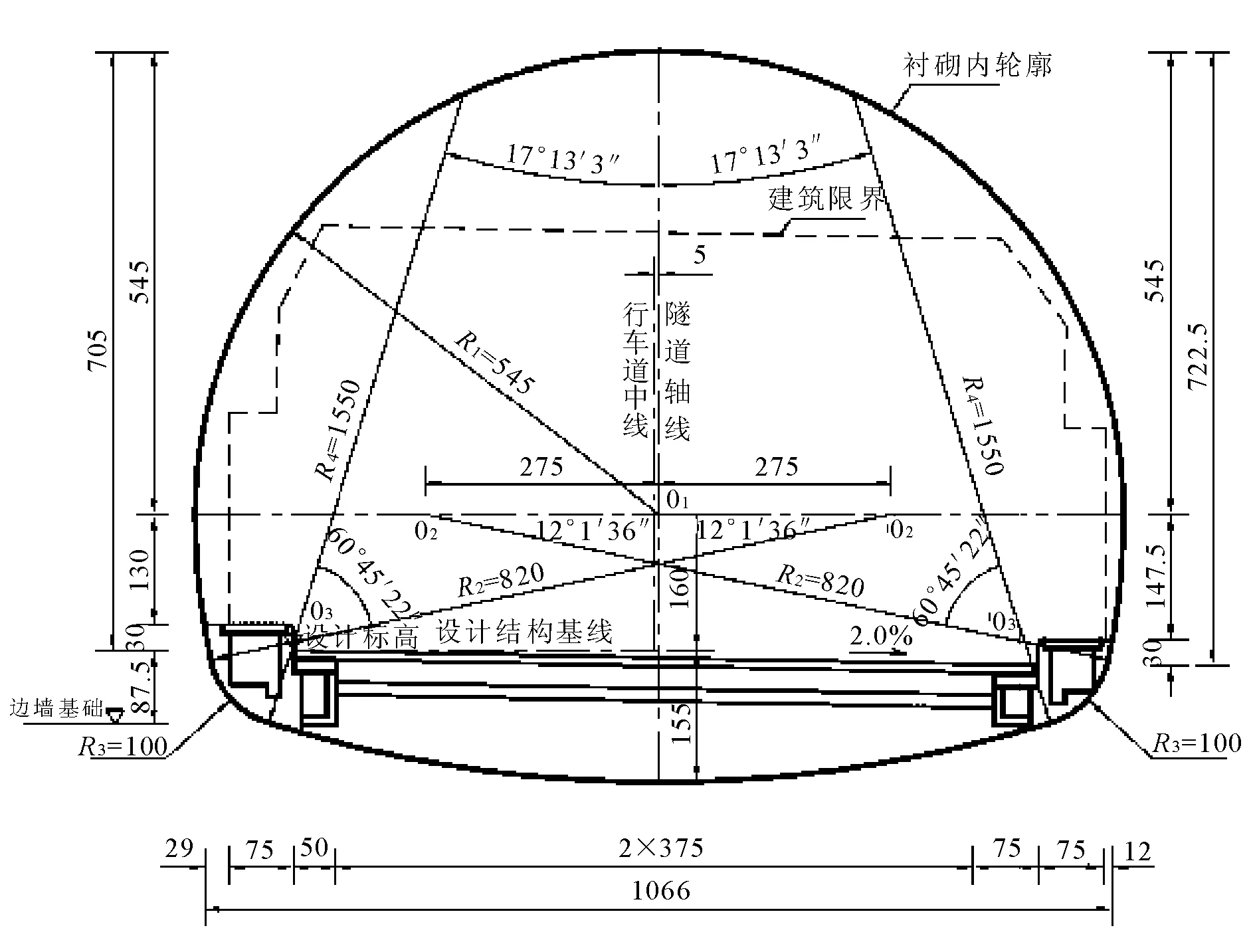
图1 兴隆隧道模型设计图(单位：cm)

2 基于流固耦合模型的隧道围岩稳定性研究

2.1 隧道流固耦合模型计算的基本假定

渗流场模型假定：

(1) 将隧道的围岩假设为各向同性、均质的等效连续渗透介质。

(2) 在隧道为开挖前，隧道内的孔隙水处于静止的状态，在水库以下的岩体处于饱和状态，在隧道完成开挖后，隧道的围岩处于稳定渗流状态。

(3) 隧道围岩地下水流服从Darcy渗流定律。

应力场基本假定：

(1) 计算中围岩采用Mohr-Coulomb弹塑性本构模型。

(2) 隧道的围岩初始应力场部考虑其应力场，仅考虑其自身重力。

2.2 隧道涌水量预测方法比较及计算

兴隆隧道的富水段围岩稳定性与隧道围岩上方的水库含水率及水库距离隧道拱顶位置有关，常规的隧道涌水量计算方法共有4种方法[11-14]。

(1) 经验公式法：

Qs=L×K×H(0.676-0.06K)

(1)

其中主要采用实际工程抽水、压水等实验资料来确定经验公式中水文地质的参数。

式中：K为隧道围岩渗透系数，m/d；L为隧道涌水段的计算长度，m；H为水头至隧道横断面等价圆中心的距离，m。

(2) 地下水动力法：

① 经验公式：

Q0=L(0.0255+1.9224×H×K)

(2)

② 古德曼公式：

(3)

式中：d为隧道横断面等价圆的直径，m；Q0为隧道通过涌水地段的最大涌水量，m3/d。

K、L、H的含义与公式(1)的含义相同。

(3) 简易水均衡法：

在确定研究范围内的大气降水量和计算范围内的地表补给面积，简易水均衡法计算的是平均涌水量，是考虑大气降水的全部或部分涌入隧道，其计算公式为：

Qcp=(1000·F·α·R)/365

(4)

式中：Qcp为隧道的平均涌水量，m3/d；F为计算范围内的地表补给面积，km3；R为在一定范围内的大气降水量，mm；可以通过当地的气象局确定；α为大气降水入渗系数。

(4) 裘布依理论公式：

(5)

式中：Qs为隧道的正常涌水量，m3/d；R为隧道涌水地段的引用补给半径，m；h为隧道内排水沟假设水深，m；r为隧道洞身横断面等价圆的半径，m。

K、L、H的含义与公式(1)的含义相同。

结合以上公式计算求解及现场实际测量，得到重庆兴隆隧道涌水量为1 940 m3/d。

2.3 隧道围岩流固耦合模型建立

2.3.1 岩土体的渗流应力耦合方程

岩土体的初始孔隙率为：

(6)

式中：v0为岩土体初始总体积；vs为岩土体初变形后总体积。

对岩土体进行不能压缩的假设，则岩土层被扰动后的土体孔隙率为：

(7)

对于小变形问题：

(8)

联立式(6)、式(7)、式(8)可得到：

(9)

在平面应变中，εz=0，所以单位体积应变：

εv=εx+εy

(10)

根据本构方程：

(11)

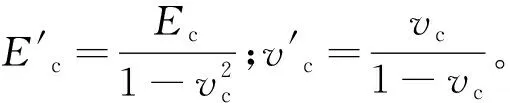
根据渗流力学中的Kozeny-Carman方程：

(12)

式中：L为常量；R为水力半径；K为渗透系数；n为孔隙率，将式(9)代入式(12)可以得到：

(13)

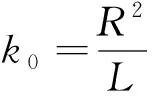
2.3.2 渗流场的控制方程

渗流场在计算时利用Darcy渗流法则，在单位面积下的渗流量公式为[15-16]：

q=k·i

(14)

式中：q为单位面积的渗透力；k为Darcy定律的渗透系数；i为水力坡度。

渗流场在计算时采用的基本方程公式如下：

(15)

式中：H表示总水头；kx、ky、kz分别表示x、y、z方向上的渗透系数；Q表示渗流场的流量；Θ表示渗流场的体积含水率；t表示时间。

隧道围岩渗流场中，稳定的渗流状态中流入和流出的量不随时间发生变化，即围岩的体积含水率不随时间变化，得到公式为：

(16)

岩土体特性的变化及隧道围岩应力状态的变化将影响着隧道围岩体积含水率的变化。体积含水率的变化与孔隙水压力的变化关系如下：

∂Θ=mw∂μw

(17)

式中：mw为阻流系数。

另外总水头可视为压力水头和位置水头之和，即:

(18)

式中：Hw为总水头；μw为孔隙水压；γ为水的重度；z为标高。

联立式(14)—式(18)可得：

(19)

当标高一定时，对时间求导后函数为零，即变为下式：

(20)

隧道围岩为二维模型，其渗流只有x、y两个方向，则根据式(20)可得到二维的渗流方程：

(21)

2.3.3 应力场的控制方程

对应力场控制方程进行方程整理，依据弹塑性力学相关理论，可求得岩土体应变场的控制方程。求解有效应力影响下的土体的平衡方程为：

σij,j+Fi-(αδijp)，j=0

(22)

式中：σij,j为应力张量；α为Biot系数；p为孔隙水压力；Fi为土体的体积力分量。

岩土体变形的几何方程为：

(23)

式中：εij为应变张量；u为位移。

岩土体应变场的本构方程采用弹塑性本构方程，本构方程的增量表达式为：

(24)

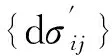
假设岩体只发生孔隙变形，则孔隙度与体积应变的关系为：

(25)

式中：体积应变εv=εx+εy+εz；φ0为初始孔隙度。

通过对有效应力方程和弹塑性本构方程的联立得出应力与应变的关系方程，该方程表示出应力场是通过应力的改变影响岩体的应变而作用于渗流场的。

2.4 隧道围岩流固耦合模型有限元分析

2.4.1 兴隆隧道耦合模型建立

兴隆隧道下穿水库段，水库位于隧道顶部30 m处。本文采用COMSOL Multyphysics有限元数值模拟软件对隧道施工完成后，隧道流固耦合隧道围岩稳定性分析。隧道假设为半径为5 m的圆形隧道，即r0=5 m，隧道水头高为30 m，即ha=30 m，其模拟比例及网格划分如图2所示。

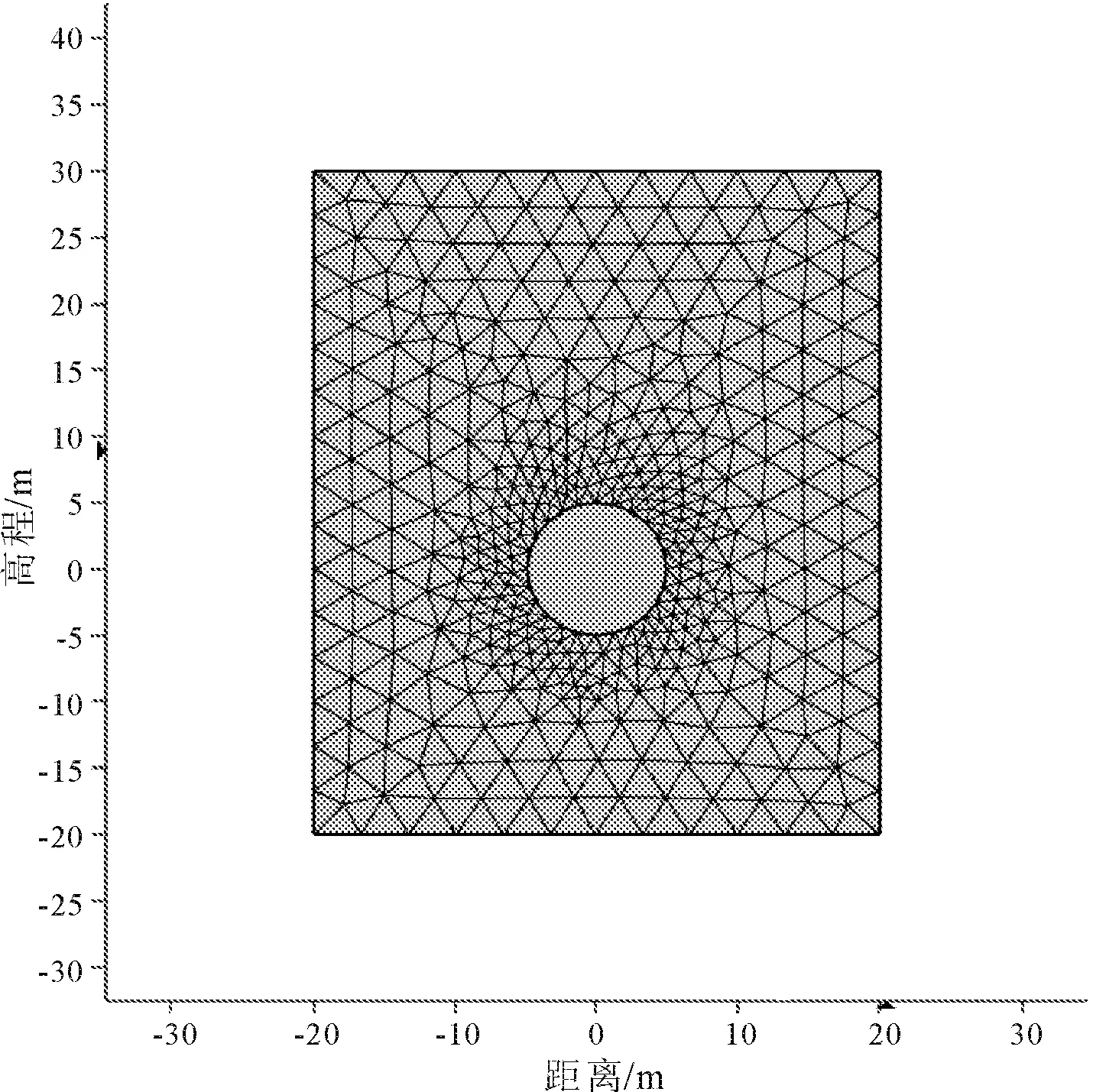
图2 兴隆隧道有限元模拟示意图

兴隆隧道围岩主要分为强风化泥岩、中风化泥岩、强风化砂岩及中风化砂岩，具体的物理性质参数如表1所示。

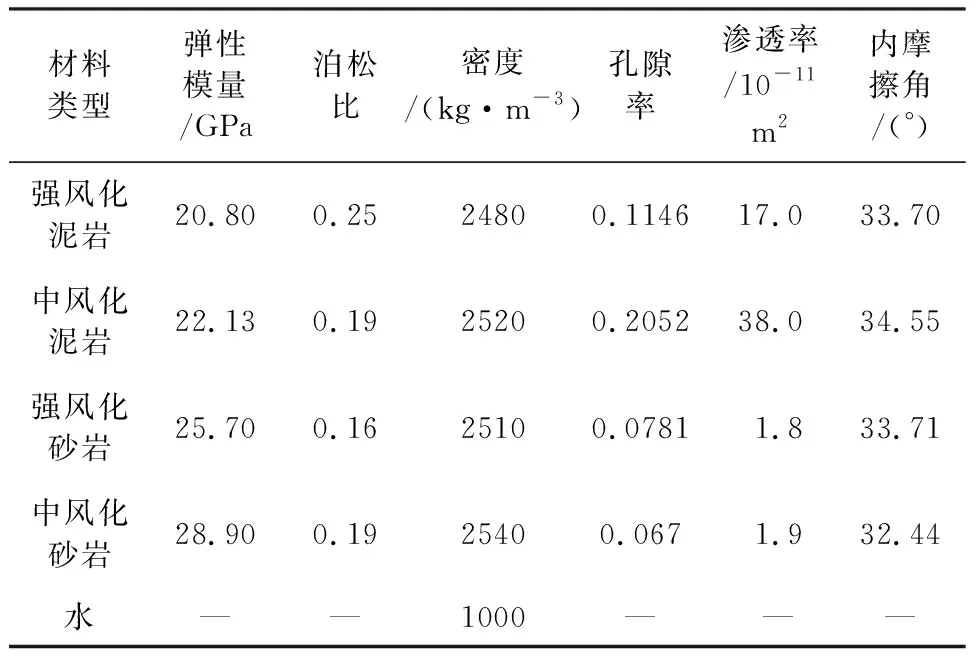
表1 兴隆隧道围岩物理性质参数

2.4.2 流固耦合计算结果分析

隧道在施工完成后由于上部水库作用发生隧道围岩的流固耦合，计算隧道流固耦合围岩所承受的压力，其中图3表示隧道施工完成后发生渗流时，隧道围岩的受力情况。

图3 隧道围岩受力示意图(MPa)

选取隧道中三个点进行围岩受力分析，其坐标点如4图所示，得到如图5所示的曲线示意图。

图5中横坐标表示运算的时间步，纵坐标表示的是测试位置所承载的压力变化。可以得到，三个位置的压力变化速率大致相同，但承载的压力不同，在流固耦合发生一段时间后，所承载的压力不再发生变化保持稳定。

图5中可以得到，在以圆形隧道为模型的隧道底部受到的压力最大，其次为隧道的拱腰处受到的压力，隧道在拱顶处所受到的压力最小。其中拱底受到的压力为3.87 MPa，拱腰处受到的压力为3.19 MPa，拱顶处受到的压力为2.34 MPa。

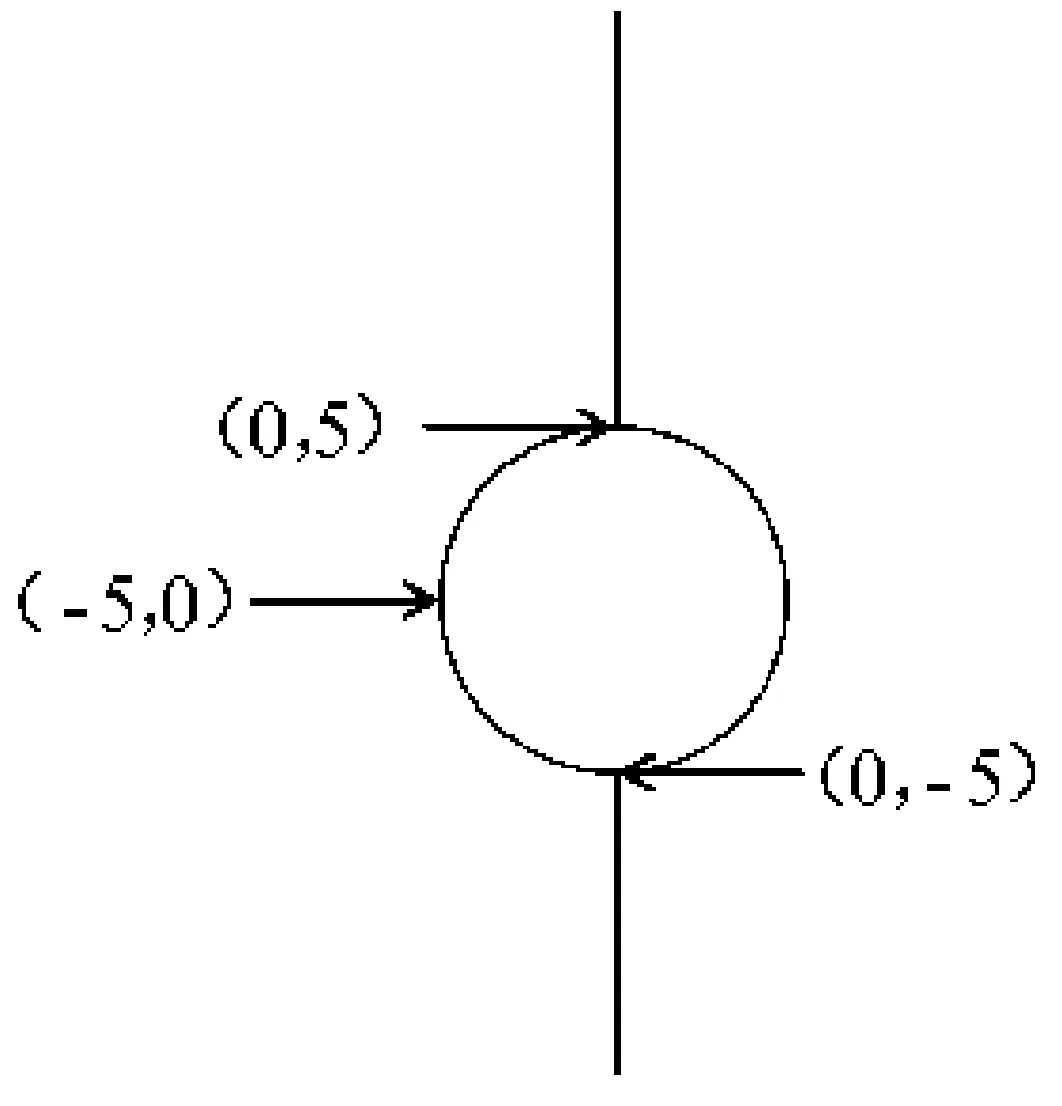
图4 隧道围岩受力测试点示意图

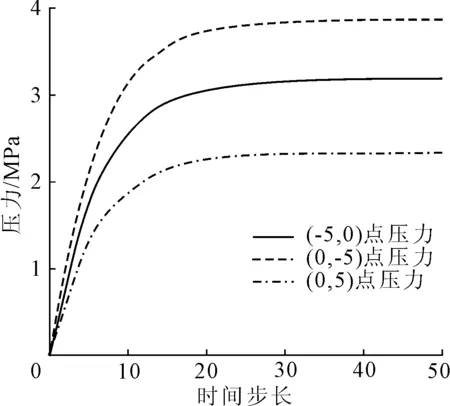
图5 隧道围岩受力测试点曲线示意图

改变水库距隧道顶部的距离，判断水头的高度变化对隧道各个位置所受的压力大小的影响，分别将水头高度设置为30 m、20 m及10 m，求在不同的水头高度下所承载的压力。

从图6中可以得到，对于(-5，0)测试点即位于隧道拱腰处的测试点，水头高度的变化对于此位置所受的压力产生变化，但变化不大。L1、L2及L3分别表示隧道在顶部距离水库底部30 m、20 m及10 m水头高度下所受的压力，其数值分别为3.19 MPa、3.09 MPa及2.99 MPa。

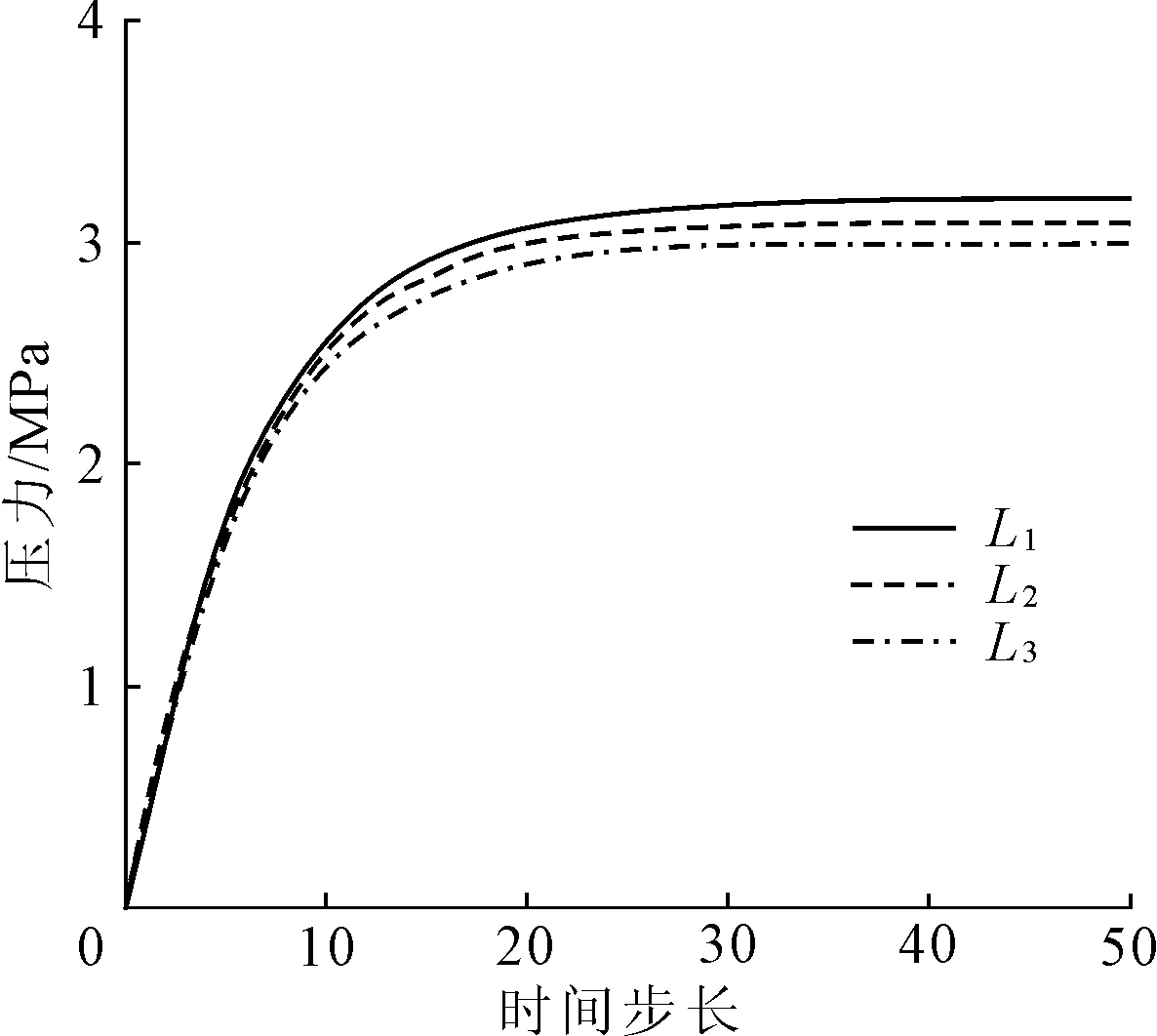
图6 隧道(-5，0)测试点在不同水头高度作用下受力变化示意图

从图7中可以得到，对于(0，5)测试点即位于隧道拱顶处的测试点，水头高度的变化对于此位置所受的压力产生变化，变化同样不大。在L1、L2及L3分别表示隧道在顶部距离水库底部30 m、20 m及10 m水头高度下所受的压力，其数值分别为2.34 MPa、2.24 MPa及2.14 MPa。

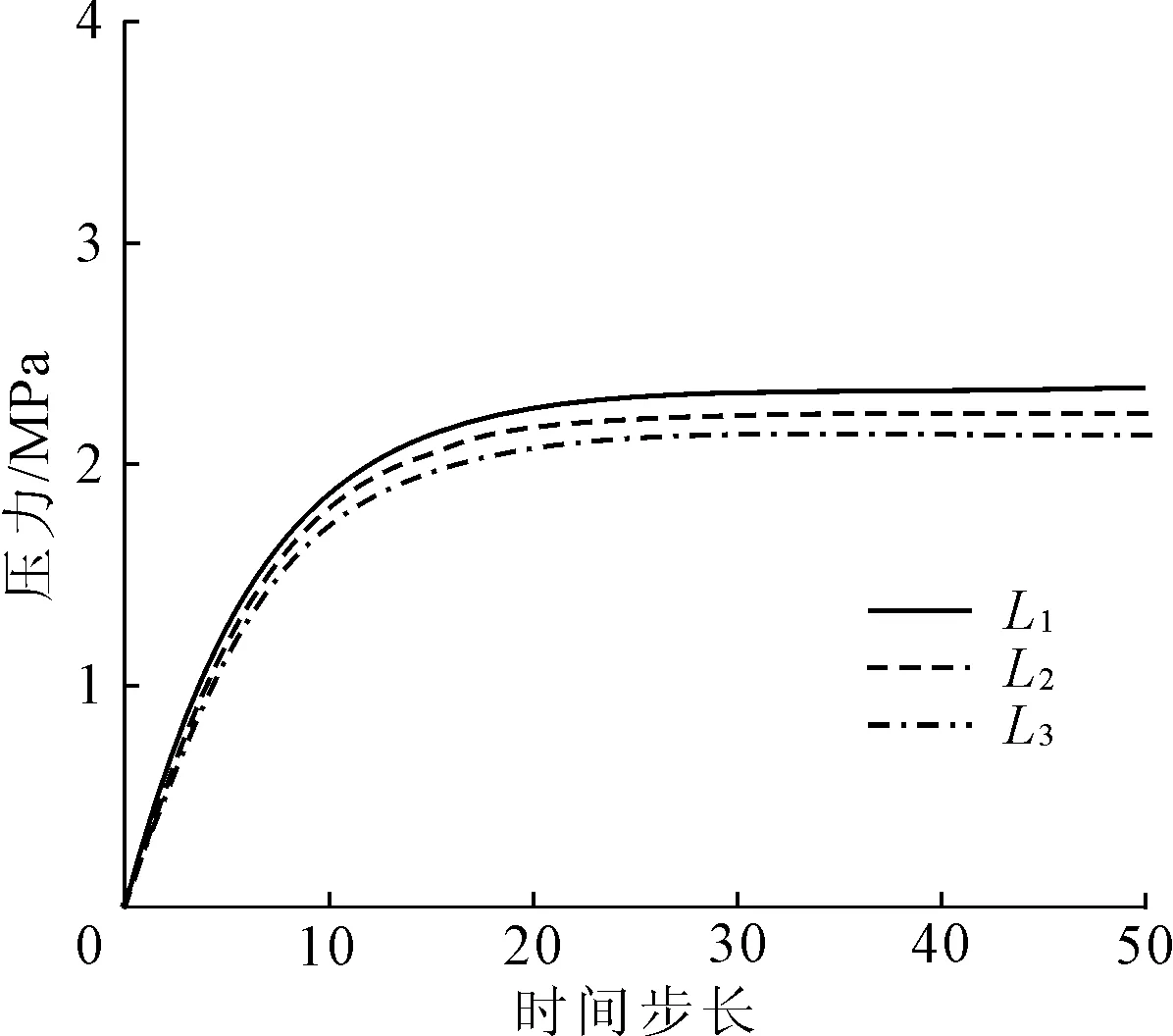
图7 隧道(0，5)测试点在不同水头高度作用下受力变化示意图

从图8中可以得到，对于(-5，0)测试点即位于隧道拱底处的测试点，水头高度的变化对于此位置所受的压力产生变化。L1、L2及L3分别表示隧道在顶部距离水库底部30 m、20 m及10 m水头高度下所受的压力，其数值分别为3.84 MPa、3.77 MPa及3.67 MPa。

图8 隧道(-5，0)测试点在不同水头高度作用下受力变化示意图

3 结 论

(1) 针对重庆兴隆隧道，因其下穿的水库存水量大，造成隧道围岩的涌水量巨大，根据计算及实际测量，得到涌水量平均数值为1 940 m3/d。在实际工程中，应将测量所得涌水量与计算值相比较得到隧道涌水量的最优解。

(2) 按照隧道的实际工况，对隧道的不同位置所承载的压力利用有限元软件进行计算，得到结论，隧道的拱底承载的压力大于拱腰及拱顶位置的压力，数值分别为3.87 MPa、3.19 MPa及2.34 MPa。可以得到在实际工程中，不同位置的围岩损伤程度不同，拱底位置应进行保护。

(3) 根据不同水头高度进行参数分析，发现隧道的各个位置都随水头的高度升高承载的压力变大，其变化速率大致相同。