半无限封闭含水层非稳定渗流的“浸润锋面”最大距离研究

刘 茂，郭 华，王双峰，张 鹏

(四川省地质工程勘察院集团有限公司，四川 成都 610072)

半无限单一均质土层的渗流问题研究的较多，现阶段理论也较成熟，但是对于半无限封闭含水层的渗流问题相对研究的较少，且大部分都是研究坝体的渗流问题。毛昶熙等[1]基于堤身浸润线呈斜直线向前推进的假定，推导了不透水地基和透水地基(双层和多层)上的堤防非稳定渗流浸湿距离L的简化计算公式，但此公式中采用的补给系数受多种影响因素的影响；吴世余[2]推导了双层地基(下为砂层、上为黏性土的覆盖层)的非稳定渗流方程及在特殊条件下的解析解；我国《堤防工程设计规范》[3](GB 50286—2013)假设浸润线锋面近似呈直线状，推导了不透水层地基浸润线锋面t时刻的最大距离公式；针对透水地基的浸润线锋面研究较少，且理论也不成熟，谢斯塔克夫假定上游斜体的渗流全部垂直下渗进入到地基(透水层)而给出了渗流量的计算式，但与实际情况误差较大[4]，王韦等[5]假定上游斜体有部分渗流进入地基(透水层)给出渗流量的计算式，前人研究都是围绕着渗流量进行研究，缺乏对坝体浸润线锋面的相关研究，对透水层地基的浸润线锋面的研究鲜见报道。

前人关于透水地基坝体的相关渗流研究的较多，且大多为稳定渗流问题，还有主要是针对渗流量进行研究，浸润锋面研究的更少，且没有很好的简易公式，本文借鉴透水地基均质坝体结构思想，参考岸坡的双元结构，提出了“半无限封闭含水层结构”的概念，即：上为半透水层(黏性土)下为透水含水层(粉砂层)的地质结构被河流切割而形成。随着计算机的发展，数值法在地下水分析中被广泛使用，本文采用数值法进行非稳定渗流的研究，数值法主要包括有限差分法、有限元法、边界元法、离散元法和流形元法等[6-7].本文利用Autobank有限元程序，采用二维渗流理论和相关的有限元理论，借鉴坝体渗流研究中的“浸润锋面”概念，针对半无限封闭含水层非稳定渗流的浸润锋面最大距离的影响因素进行了一系列的研究，为具有该结构岸坡的渗流规律提供一定的参考意义，为控制岸坡渗流提供一定依据。

1 理 论

1.1 渗流理论

二维渗流的一般控制微分方程为[8]：

(1)

式中：H总为总水头；Kx为x方向的渗透系数；Ky为y方向的渗透系数；Q为施加的边界流量；θ为单位体积含水率；t为时间。

对于有自由面的非稳定渗流，可采用平均渗流水深H的方式，即：由于微元流量流入流出差额使自由水面升降的水的体积平均分配于高度H上，得到以给水度表达的二维渗流控制微分方程，即为Boussinesq方程[9-10]，具体方程如下：

(2)

给水度除与渗透系数密切相关外，还与土的紧密度和介质的几何性质有关[4，11]，本文给水度计算采用南京水利科研院的给水度公式，公式为：

μ=1.137n(0.0001175)0.067(6+lgk)

(3)

式中:μ为给水度，或含水层的自由孔隙率；k为渗透系数,m/d；n为体积孔隙率。

1.2 有限元理论

对控制方程应用加权余量的伽辽金方法，可以得到二维渗流的有限元方程[8,12]：

(4)

式中:[B]为梯度矩阵；[C]为单元渗透系数矩阵；[H]为节点水头矩阵；〈N〉为插值函数向量；q为穿过单元边界的单元流量；τ为单元厚度；t为时间；λ为存储项，对瞬态顺流等于mwγw；A为在单元面积上的求和符号；L为在单元边界长度上的求和符号。

2 模型建立

假设条件：① 各含水层均质、各向同性、土层水平且侧向无限延伸; ② 渗流为二维流且服从达西定律；③ 河水位上升为瞬时完成，不考虑入渗补给；④ 初始潜水位与河道的初水位(h0)水平[13]；⑤ 渗流模型底部透水性可忽略不计(或者采取很小的值)。

依据以上假设条件，具体模型如图1所示。

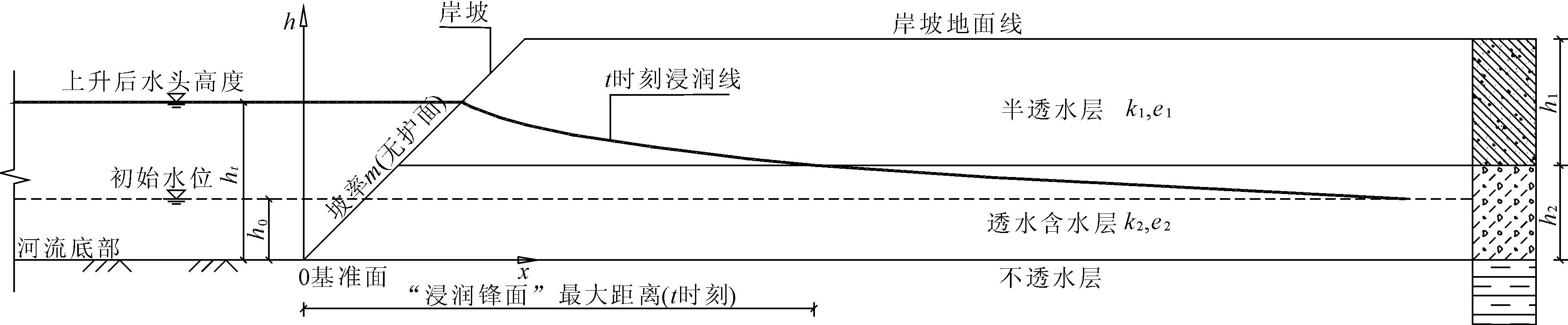
图1 河道切割形成的半无限密闭含水层结构

鉴于三角形单元能较好地适应渗流场复杂的边界形状和非均质土层分布，因此，单元采用常用的三角形单元，本文模型划分的网格密度为3.03，基本上能满足模型的精度要求。

3 浸润锋面最大距离影响因素分析

3.1 渗透系数的影响

本渗流模型采用直立岸坡，含水层渗透系数k2分别取0.002 m/s，0.004 m/s和0.006 m/s，孔隙率e2=0.335，相对弱透水层渗透系数k1分别为0.000 04 m/s、0.000 08 m/s、0.000 16 m/s、0.000 40 m/s、0.000 80 m/s，孔隙率e1=0.395，初始水位为12 m，瞬时上升的水头为28 m，计算的非稳定渗流浸润锋面距离见图2和图3。

图2 不同持续时间的浸润锋面最大距离与渗透系数k1关系曲线

由图2可知，短时间渗透，随着上部半透水层的渗透系数增大呈凹曲线型式，上部半透水层渗透系数越小下降越快，随着渗透系数增大，浸润锋面最大距离呈近直线增长，且斜率越来越大；较长时间渗透，随着上部半透水层的渗透系数增大基本上呈线性增长趋势(渗透系数极小的除外)；随着下部透水层渗透系数的增大，凹曲线下降部分的历时越来越短。

图3 不同渗透系数的浸润锋面最大距离随渗流时间关系曲线

由图3可知，浸润锋面最大距离受下部透水层的渗透系数控制，受上部半透水层的渗透系数影响很小。短时间渗透，浸润锋面最大距离随下部透水层渗透系数增大呈减速增长趋势，长时间渗透，浸润锋面最大距离随下部透水层渗透系数增大呈指数趋势增长，短时间和长时间渗透的界定时间为60 h。

3.2 透水含水层厚度的影响

本渗流模型采用直立岸坡，透水含水层渗透系数k2=0.004 m/s，孔隙率e2=0.335，相对弱透水层渗透系数k1=0.000 04 m/s，孔隙率e1=0.395，初始水位为12 m，瞬时上升的水头为28 m，含水层厚度取0.5 m～20.0 m，计算的非稳定渗流浸润锋面距离见图4、图5和图6。

由图4可知，浸润锋面最大距离随透水含水层厚度增厚呈现先增大再减小最后趋于线性增长的趋势。

初始水位低于下部透水层底面时，下部透水层厚度小于等于初始水位与透水层顶的距离的一半时，浸润锋面最大距离随土层厚度呈上凸幂函数增长。下部透水层厚度大于初始水位与透水层顶距离一半的1/2～3/4时，渗流时间小于24 h时，随着下部透水层厚度增大，浸润锋面最大距离减小，渗流时间大于24 h时，随着下部透水层厚度增大，浸润锋面最大距离呈现先减小再增大趋势，下部透水层厚度为初始水位与透水层顶距离一半的3/4～1时，浸润锋面最大距离呈近直线下降，且下降的速率随着渗流时间增长而增大。

初始水位高于下部透水层底面时，随着下部透水层厚度的增大，浸润锋面最大距离呈近线性增长，且随着渗透时间推移，增长速率增大。

图4 不同持续时间的浸润锋面最大距离与含水层厚度关系曲线

图5 不同含水层厚度的浸润锋面最大距离与渗流时间关系曲线(初始水位低于下部透水层底面)

由图5可知，初始水位低于下部透水层底面时，渗流时间小于24 h时，浸润锋面最大距离为下部透水层厚度等于初始水位与透水层顶的距离的一半；渗流时间大于24 h时，浸润锋面最大距离为下部透水层厚度等于初始水位与透水层顶的距离的3/4处。

下部透水层厚度小于等于初始水位与透水层顶的距离的一半时，浸润锋面最大距离随土层厚度增大呈近线性增长；下部透水层厚度大于初始水位与透水层顶的距离的一半时，浸润锋面最大距离随土层厚度增大呈上凸幂函数趋势增长。

由图6可知，初始水位高于下部透水层底面时，随着渗透时间的推移，浸润锋面最大距离呈上凸幂函数趋势增长，下部透水层厚度越厚，浸润锋面最大距离增长速率增大。

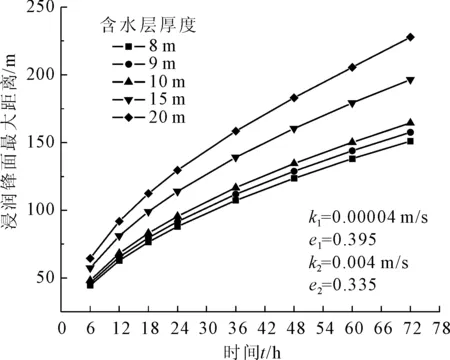
图6 不同含水层厚度的浸润锋面最大距离与渗流时间关系曲线(初始水位高于下部透水层底面)

3.3 初始水位在透水层位置的影响

本模型采用直立岸坡，透水含水层厚度为20 m，含水层渗透系数k2=0.004 m/s，孔隙率e2=0.335，相对弱透水层渗透系数k1=0.000 04 m/s，孔隙率e1=0.395。初始水位分别取12 m、13 m、14 m、15 m、16 m、17 m、18 m，瞬时上升的水头高度为28 m，计算的非稳定渗流浸润锋面距离见图7和图8。

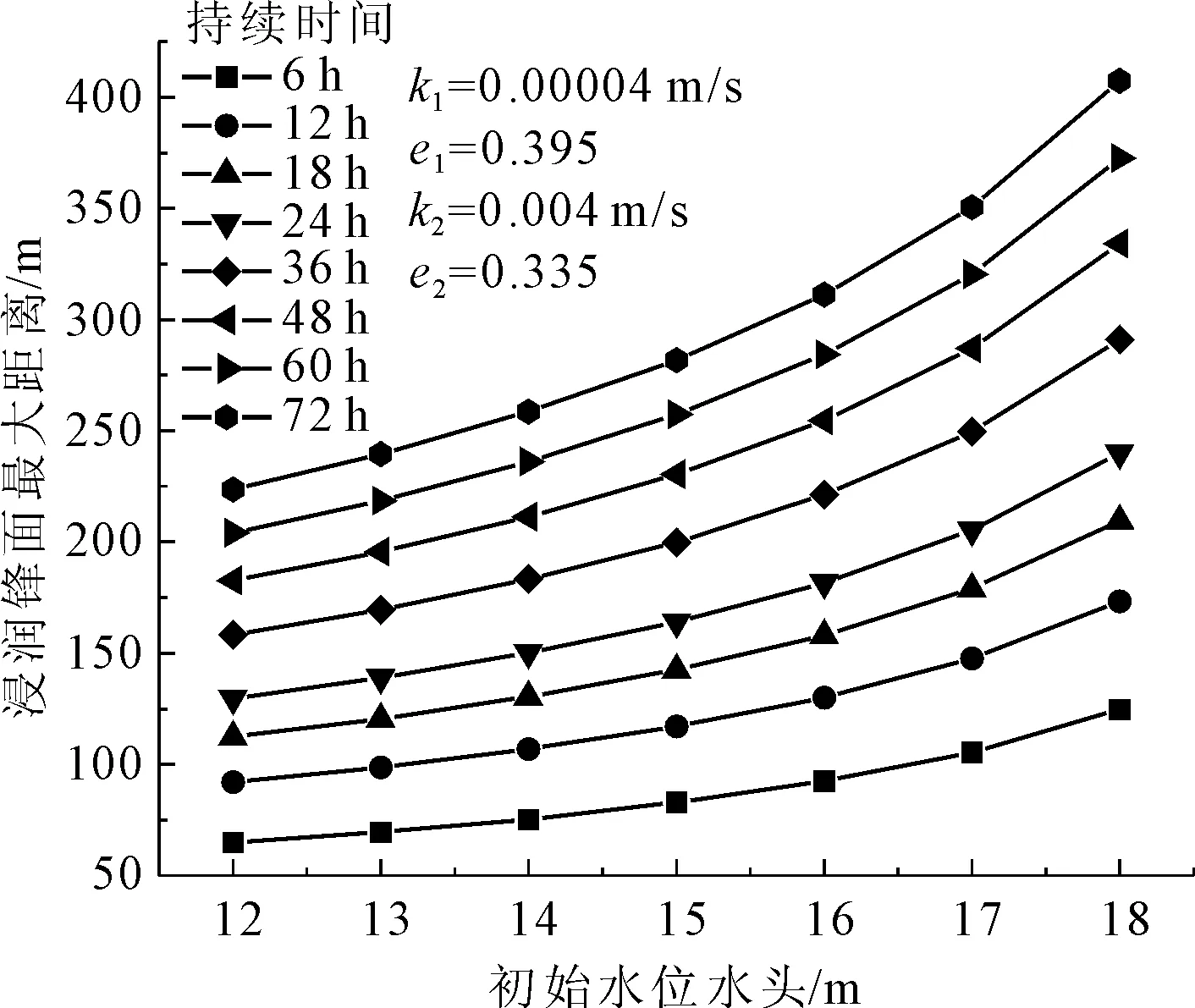
图7 不同持续时间的浸润锋面最大距离与初始水位关系曲线

由图7可知，浸润锋面最大距离随位于透水含水层的初始水位增高呈指数增长趋势，且渗流时间越长，浸润锋面最大距离增长越慢。

由图8可知，浸润锋面最大距离随渗流时间呈上凸幂曲线增长，且随着水头的增高，浸润锋面最大距离增长越快。

3.4 斜坡坡率的影响

本模型采用倾斜岸坡，透水含水层渗透系数k2=0.004 m/s，孔隙率e2=0.335，相对弱透水层渗透系数k1=0.000 04 m/s，孔隙率e1=0.395，初始水位分别取12 m，瞬时上升的水头高度为28 m，倾斜岸坡坡率分别为0.00、0.25、0.50、0.75、1.00，计算的非稳定渗流浸润锋面距离见图9和图10。

图8 不同初始水位的浸润锋面最大距离与渗流时间关系曲线

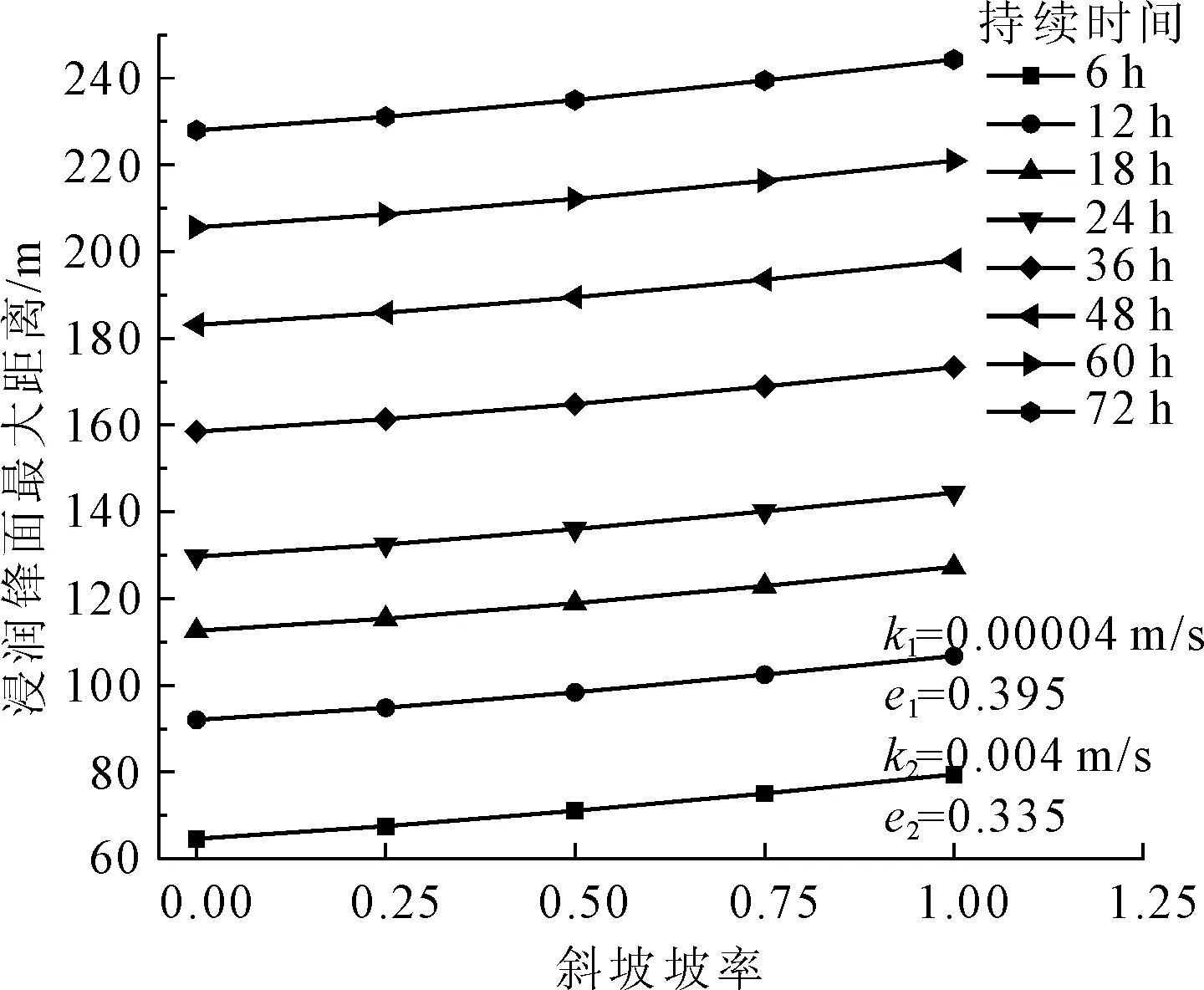
图9 不同持续时间的浸润锋面最大距离与岸坡坡率关系曲线

由图9可知，浸润锋面最大距离受斜坡坡率影响较大，随着岸坡斜率的增大呈近线性增长，且增长的斜率基本不随渗透时间变化。

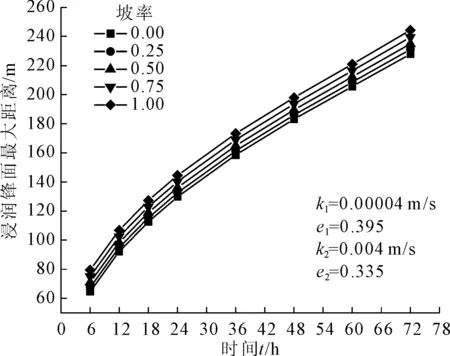
图10 不同岸坡坡率的浸润锋面最大距离与渗流时间关系曲线

由图10可知，浸润锋面最大距离随着渗流时间增长，基本呈上凸幂函数曲线增长，曲线形状基本不受斜坡坡率影响，但随着斜率增大而增大，增大的幅度基本一致。

3.5 水头高度的影响

本模型采用直立岸坡，透水含水层渗透系数k2=0.004m/s，孔隙率e2=0.335，相对弱透水层渗透系数k1=0.000 04 m/s，孔隙率e1=0.395，初始水位分别取12 m，瞬时上升的水头高度分别为21 m、22 m、23 m、24 m、25 m、26 m、27 m、28 m，计算的非稳定渗流浸润锋面距离见图11和图12。

图11 不同持续时间浸润锋面最大距离与水头关系曲线

图12 不同水头浸润锋面最大距离与渗流时间关系曲线

由图11和图12可知，浸润锋面最大距离随着水头高度的增大呈上凸幂函数增长，同一水头随着渗透时间的增长，浸润锋面最大距离增长越慢。

4 影响浸润锋面最大距离的因素分析

由以上影响因素分析可知，浸润锋面最大距离的影响因素本次考虑如下六个因素：透水层渗透系数、初始水位、透水层厚度、水头高度、坡率、渗流时间，每个影响因素都考虑5个水平，通过等水平正交试验设计[14-15]，采用L25(56)等水平正交表进行试验设计，利用极差分析法可以直观简便地分析实验结果，确定因素的主次，极差越大，该因素对实验结果的影响越大，正交试验设计的因素及水平见表1。

表1 正交试验设计的因素及水平

依据正交设计和极差分析可知：各个因素对浸润锋面最大距离影响大小顺序如下：水头高度>透水层渗透系数>透水层厚度>渗流时间>坡率>初始水位。

5 结 论

(1) 浸润锋面最大距离的影响因素主要有透水层渗透系数、初始水位、透水层厚度、水头高度、坡率、渗流时间六个影响因素。

(2) 浸润锋面最大距离受下部透水层的渗透系数控制，受上部半透水层的渗透系数影响很小；随土层厚度增厚呈现先增大再减小最后趋于线性增长的趋势；初始水位位于下部透水层范围内时，浸润锋面最大距离随初始水位增高呈指数增长趋势，且渗流时间越长，浸润锋面最大距离增长越慢；随着岸坡斜率的增大呈近线性增长，且增长的斜率基本不随渗透时间变化；随着水头高度的增大呈幂函数增长，且随着渗透时间的增长幂因素越来越大。

(3) 在未考虑复杂的水位变化过程的情况下，各个影响因素对浸润锋面最大距离影响大小顺序河渠边界如下：水头高度>透水层渗透系数>透水层厚度>渗流时间>坡率>初始水位。