状态反馈脉冲控制的福寿螺-水稻防控数学模型

2021-01-03曾夏萍梁志清庞国萍周泽文

四川师范大学学报（自然科学版） 2021年1期

曾夏萍，梁志清，庞国萍，周泽文

（玉林师范学院数学与统计学院广西高校复杂系统优化与大数据处理重点实验室，广西玉林537000）

0 引言

利用数学理论及方法研究有害物防治已经成为有害物种防治的一个重要内容.许多学者通过建立数学模型在有害生物综合治理研究方面做了大量工作［1-5］.在有害物的实际防控中，常常需要按有害物种的发展状态实施防控，当有害物种数量达到某一水平时实施杀害，这种杀害方式可用状态脉冲微分方程的理论进行研究［6］.有关状态脉冲微分方程的阶1 周期解的研究参见文献［6 -10］.这些学者的工作主要着眼于研究投放天敌、染病害虫或病毒的生物防治和喷洒农药杀虫剂（或微生物制剂）的害虫防控策略.

在一些特殊的生态环境，如稻田，福寿螺作为入侵生物，已经在农业生产方面产生了一系列的危害和影响，造成了近年来世界范围内水稻生产难以估量的损失.稻田福寿螺已成为我国局部水稻产区有害生物的重点防控对象，设法有效防治、控制稻田福寿螺的入侵和危害是一项刻不容缓的重大研究任务.防治福寿螺的同时，必须兼顾对水稻及其他稻田生物的保护，尽量避免使用高毒的化学农药，这方面的生态学者一致认为针对福寿螺生长于稻田的这种特殊生态环境，福寿螺防控应采用生物防控和物理防控［11-16］.物理防治以放茶麸或金腰箭提取物杀灭螺为主，生物防治以稻田中放养吃螺鱼类的鸭子为主，防止福寿螺的过度繁殖.文献［11 -16］针对福寿螺的防控做了许多工作.但对福寿螺防控的研究工作大多数是从生态角度及对有害物的防控手段等方面展开，属于定性的研究.用数学模型研究防治福寿螺和对水稻保护作动力学方面的研究目前还比较少.运用生物防控和物理防控综合防治控制福寿螺过度繁殖的数学模型研究目前也少见.

基于以上的生物学背景，本文利用数学理论及方法研究具有状态脉冲反馈控制的福寿螺-水稻的生态系统.在福寿螺-水稻的捕食与被捕食种群系统的基础上，通过在稻田中放养鸭子，结合福寿螺发展的“状态”脉冲喷洒茶麸水控制福寿螺过度繁殖的方法，建构具有脉冲状态控制的捕食与被捕食种群模型，利用微分方程几何理论及后继函数法对模型进行分析，获得在稻田中将福寿螺控制在水稻可以承受临界值范围之内的生物治理策略.

捕食与被捕食关系是学者一直关注的热点，具有Holing 功能性反应的捕食与被捕食模型形式如下

其中，g（x）为食饵种群的内禀增长率，dy为捕食者种群的死亡率，φ（x）为捕食者的功能性反应函数.

1 模型的建立

在捕食-被捕食系统的基础上，考虑具有状态反馈脉冲控制的福寿螺-水稻的生态系统，合理利用福寿螺净化水体，同时又防止其过度繁殖破坏水稻生长.因为考虑到2 种或多种方法结合使用效果会更理想，所以在模型（2）中引入福寿螺的生物防治，即在稻田中饲养鸭子，鸭子可以吃掉幼螺；物理防治，即当福寿螺超过一定的阈值时，脉冲喷洒一定量的茶麸水.多种方法配合使用，逐渐达到和保持福寿螺和水稻之间的种群动态平衡，取得持续控制福寿螺的结果，得到如下的具有状态脉冲控制的福寿螺过度繁殖防控数学模型：

捕食-被捕食模型可用于描述福寿螺-水稻的关系，福寿螺为被捕食种群，水稻为食饵种群，是福寿螺的生活资源.在模型（2）中，x表示水稻在时刻t的密度，y表示福寿螺在时刻t的密度.假设在福寿螺生长初期，使用稻田中饲养鸭子抑制福寿螺的增长，单位时间鸭子吃螺率为α（α∈（0，1）），福寿螺数量达到一定数量时会对水稻产生危害，这个数称之为临界值，记为h.当福寿螺数量达到时，采用喷洒茶麸水的脉冲方式降低福寿螺数量，杀死的福寿螺数量与种群数量成正比，记比例系数为p（p∈（0，1））.于是以福寿螺发展的“状态”，考虑生物杀螺和物理杀螺相组合的福寿螺防控措施，得到状态依赖的脉冲组合模型.

利用后继函数研究系统（2）周期解的存在性、唯一性和稳定性，寻找放养鸭子和喷洒茶麸水相结合的福寿螺防控策略.

2 预备知识

定义2.1［6］考虑状态脉冲微分方程称由状态脉冲微分方程（3）所定义的解映射所构成的＂动力学系统＂称为＂半连续动力系统＂，记为（Ω，f，φ，M），规定系统的映射初始点P不能在脉冲集上，P∈Ω =-M｛x，y｝，φ 为连续映射，φ（M）=N，φ 称为脉冲映射，这里M｛x，y｝和N｛x，y｝为=｛（x，y）∈R2：x≥0，y≥0｝平面上的直线或曲线.M｛x，y｝称为脉冲集，N｛x，y｝称为相集.

定义2.2（˜x，˜y）为状态脉冲微分方程的平衡态（奇点），若：

1）若（˜x，˜y）∉M｛x，y｝，有f（˜x，˜y）=0，g（˜x，˜y）=0；

2）若（˜x，˜y）∈M｛x，y｝，有f（˜x，˜y）= 0，g（˜x，˜y）=0，且α（˜x，˜y）=β（˜x，˜y）=0.

1）π（P，0）=P；

2）π（P，t）对P和t均连续；

3）（π（P，t1），t2）=π（P，t1+t2），单参数π（P，t）称为P的运动轨道.

定义2.4对状态脉冲微分方程（3）定义的半连续动力系统，映射f（P，t）：Ω→Ω 称其为自身映射，它包括2 个部分：

1）记下面方程初值为P的Poincarê 映射为π（P，t），有

如果f（P2，t）∩M｛x，y｝=Ø，则半连续动力系统初值为P的映射为f（P，t）=π（P，t）.

2）如果存在时刻t1使得f（P，T1）=H∈M｛x，y｝，脉冲映射φ（H）= φ（f（P，T1））=P1∈N｛x，y｝，且f（P2，t）∩M｛x，y｝=Ø，则半连续动力系统初值为P的映射为f（P，t）=π（P，T1）+f（P1，t）.

定义2.5［6］直线M为脉冲集，直线N为相集，如图1，在相集直线N上A点坐标为（xA，（1 -p）h），设由点A出发的轨线与脉冲集交于一点A′，点A′的脉冲相点A1在相集N上，坐标为A1（xA1，（1 -p）h），定义A1称为A的后继点，称g（A）=xA1-xA为后继函数.

图1 脉冲系统（2）的后继函数Fig. 1 Successor function of（2）

定义2.6阶1 周期解若相集N中存在点H，且存在t1使得f（H，t1）=H′∈M｛x，y｝，而且脉冲映射φ（H′）=φ（f（H，t1））=H∈N，则f（H，t1）称为阶1 周期解，其周期为T1，则轨道称为阶1 环.孤立的阶1 环为阶1 极限环，如图2.

图2 脉冲系统（2）的阶1 极限环Fig. 2 Order-1 limit cycles of（2）

定义2.7设Γ=f（P，t）是脉冲系统（2）的阶1 周期解.如果对任意的ε ＞0，存在δ ＞0 和t0≥0，使得对任意点P1∈U（P，δ）∩N｛x，y｝，当t＞t0时，有ρ（f（P1，t），Γ）＜ε，ρ为半径，则称脉冲系统（2）的阶1 周期解Γ为轨道稳定的.

引理2. 1后继函数是微分方程的连续解π（x，t1）与脉冲连续函数φ（x）的复合，这是2 连续函数的复合函数，故后继函数是连续的.

引理2.2（连续函数的零点定理）设g（x）是x∈［a，b］上的连续函数，若g（a）·g（b）＜0，则至少存在一点ξ∈（a，b），使得g（ξ）=0.

引理2.3（开区间套定理）如果：

引理2.4如果相集N上2 点A（xA，（1 -p）h）和B（xB，（1 -p）h），它们的后继点分别为A1（xA1，（1 -p）h）和B1（xB1，（1 -p）h）.若A和B两点的后继函数g（A）=xA1-xA和g（B）=xB1-xB互为异号，则在A和B之间至少存在1 个阶1 周期解.

证明由状态脉冲微分方程Poincarê 映射的定义，A1（xA1，（1 -p）h）是A（xA，（1 -p）h）的后继点，故存在t1使

于是，后继函数g（A）=xA1-xA.

又B1（xB1，（1 -p）h）是B（xB，（1 -p）h）的后继点，故存在t2使

于是，后继函数g（B）=xB1-xB.

由引理2.1，至少存在一点H∈（A，B）∈N｛x，y｝使g（H）=0，g（H）=c1-c=0，即H点的后继点为本身，由定义2.4 知，系统至少存在1 个阶1 周期解.

3 无脉冲作用下系统的分析

对于系统（2），在无脉冲作用下的子系统为

经简单的计算，系统（5）有一个平凡平衡点E1（0，0），系统有唯一的正平衡点E*（x*，y*），其中

下面讨论正平衡点E*（x*，y*）的稳定性.

在E*（x*，y*）变分矩阵为

因为TrJ（E*）＜0 恒成立，可知E*（x*，y*）局部稳定.

定理3.1系统（5）的正平衡点E*（x*，y*）局部渐近稳定，系统无闭轨，从而没有极限环.

证明取B=（xy）-1，则

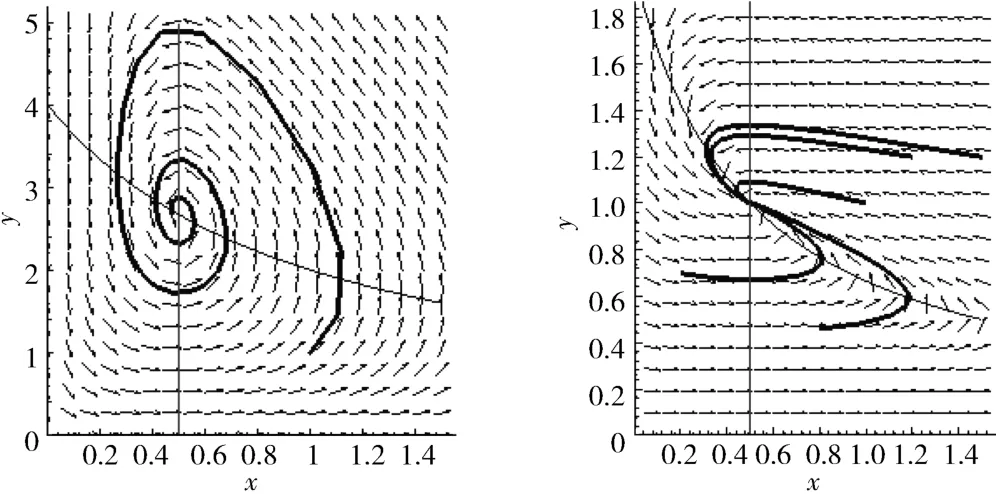
图3 系统（5）的系统的相图Fig. 3 Phase diagram of system（5）

4 脉冲系统的定性分析

在没有脉冲作用下系统（5）的正平衡点E*（x*，y*）是全局渐近稳定的焦点或结点.下面利用微分方程几何理论及后续函数方法，按正平衡点E*（x*，y*）的类型研究脉冲系统（2）周期解的存在唯一性和稳定性.

4.1 E（x，y*）为焦点

情况1h≤y*.

定理4.1若h≤y*，则脉冲系统（2）存在唯一的阶1 周期解，且阶1 周期解是轨道稳定.

证明当h≤y*时，直线y=h在y=y*下方，如图4.

这是脉冲集在直角坐标系中为y=h轴在x轴右侧的集合.

这是脉冲集在直角坐标系中为y=（1 -p）h轴在x轴右侧的集合.

先证阶1 周期解的存在性.对N上的点A，过A的轨线交y=h于A′，脉冲到A1∈N，A1为A的后继点，且xA1＞xA，后继函数g（A）=xA1-xA＜0.

同理，图4 中B1为B的后继点，且xB1＜xB，后继函数g（B）=xB1-xB＜0.

由引理2.3得，在A与B之间∃H，使g（H）=0.H点对应的坐标为（xH，（1-p）h），此时过H的轨线交y=h后脉冲到H点，说明系统（2）存在阶1周期解.

图4 对h≤y*时，脉冲系统（2）阶1 周期解的存在性Fig. 4 Existence of order-1 periodic solutions of system（2）for h≤y*

再证唯一性.在A与B之间任意取两点I，J，不妨设I＜J，则xA＜xI＜xJ＜xB.过I的轨线交直线y=h于I1，脉冲后交直线y=（1-p）h于I+.过J的轨线交直线y=h于J1，脉冲后交y=（1-p）h于J+，如图5.

图5 对h≤y*时脉冲系统（2）阶1 周期解的唯一性Fig. 5 Uniqueness of order-1 periodic solutions of system（2）for h≤y*

由xI＜xJ得xI+＜xJ+.对后继函数g有

从而g（I）单调递减函数，故函数g（I）的根存在唯一，进而脉冲系统（2）的周期解存在唯一.

下面证阶1 周期解得轨道稳定性.

设从A1出发的轨线交直线y=h于点A2，脉冲后到直线y=（1 -p）h的点A3，从A3出发的轨线交直线y=h于A4，脉冲后到直线y=（1 -p）h的A5，如此继续下去得到2 个序列：

同理，从点B1出发的轨线交直线y=h于点B2，脉冲后到直线y=（1 -p）h的点B3，从B3出发的轨线交直线y=h于B4，脉冲后到直线y=（1 -p）h的点B5，如此继续下去得到2 个序列，见图6.

上面的序列满足如下条件：

于是

图6 序列｛A2n-1｝，｛A2n｝，｛B2n-1｝，｛B2n｝Fig. 6 Sequences｛A2n-1｝，｛A2n｝，｛B2n-1｝，｛B2n｝

在H的左边附近任取一点Q0（xQ0，（1-p）h），不妨设Q0在A1与H之间，从而xA1＜xQ0＜xH.由｛xA2n+1｝的单调递增性得：存在n0，使得xA2n0+1＜xQ0＜xA2n0+3，从Q0出发的轨线交脉冲集于Q′0，相点为Q1（xQ1，（1-p）h），易知相点Q1在A2n0+3到A2n0+5之间，从而xA2n0+3＜xQ′0＜xA2n0+5.从Q1出发的轨线交脉冲集于Q′1，相点为Q2（xQ2，（1-p）h），易知相点Q2在A2n0+5到A2n0+7之间，从而xA2n0+5＜xQ′2＜xA2n0+7.如此进行下去得一个点列｛Qk｝，k=0，1，2，…，见图7，满足以下条件：

在H的右边附近任取一点P0（xP0，（1 -p）h）.不妨设P0在H与B1之间，从而xH＜xP0＜xB1.由｛yB2n+1｝的单调递增性得：存在n0，使得xB2n0+3＜xP0＜xB2n0+1，从P0出发的轨线交脉冲集于，相点为P1（xP1，（1 -p）h），易知相点P1在B2n0+5到B2n0+3之间，从而xB2n0+5＜xPQ0＜xB2n0+3.

从P1出发的轨线交脉冲集于P′1，相点为P2（xP2，（1-p）h），易知相点P2在B2n0+7到B2n0+5之间，从而xB2n0+7＜xP′2＜xB2n0+5.如此进行下去得一个点列｛Pk｝，k=0，1，2，…，见图7，满足以下条件：

由两边夹定理得

图7 轨线走向及序列｛Qk｝、｛Pk｝Fig. 7 Sequences｛Qk｝，｛Pk｝

综上可得，由P、Q的任意性知阶1 周期解是轨线稳定的.证毕.

情况2h＞y*，有如下结论.

设直线y=h与过点A的轨线LA相交的一个交点为Ah，记从Ah至A的轨线段为LA hA，由直线y=h、x轴、y轴及LA hA围成的区域为G，如图8.

图8 区域GFig. 8 Region G

定理4.2若h＞y*，则∃p*∈（0，1），使得：

1）当0 ＜p＜p*时，轨线最终趋向于E*（x*，y*）；

2）当p≥p*时，脉冲系统（2）存在唯一的阶1周期解，且是轨道稳定的.

证明先证p*∈（0，1）的存在性.

图9 p*的存在性Fig. 9 The existence of p*

从A′出发的轨线LA达到A，脉冲后又回到A′，从而形成周期解.记过A′且平行x轴的直线LA′：y=hA′.由函数y=（1 -p）h关于P的单调连续性，存在∃p*∈（0，1），使hA′=（1 -p*）h.

当p＜p*时，直线y=（1 -p）h在y=（1 -p*）h的上方，此时从初值出发的轨线与y=（1 -p）h可能相交也可能不交相.若轨线与y=（1 -p）h没有相交，即没有发生脉冲，轨线最终趋向于E*（x*，y*）.若轨线与y=（1 -p）h相交，即发生脉冲，则最后一次与x=xq的交点在A′与A之间，轨线最终趋向于E*（x*，y*），如图10.

图10 当p ＜p*时，轨线趋于E*Fig. 10 Trajectory tendency to E*for p ＜p*

当p=p*时，在脉冲的作用下轨线LA在直线y=（1 -p*）h与y=h之间的部分与AA′构成一个阶1 周期解.当p＞p*时，从初始点（x（0，y（0））∈G0出发的轨线与脉冲集的交点在点A右侧.

在图11 中，从C出发的轨线交脉冲集于点C′，相点为C1，C1为C的后继点，且xC1＞xC，后继函数f（C）=xC1-xC＞0.

同理，图11 中的B1为B的后继点，且xB1＜xB，后继函数f（B）=xB1-xB＜0.

由引理2.3 知脉冲系统（2）存在阶1 周期解存在.

图11 当p ＞p*时，系统（2）阶1 周期解的存在性Fig. 11 Existence of order-1 periodic solutions of system（2）for p ＞p*

用定理4.1 的方法可证得阶1 周期解的唯一性和稳定性.

4.2 E（x，y*）为结点

情况1h≤y*，有如下结论.

定理4.3如果h≤y*，则脉冲系统（2）存在唯一的阶1 周期解，且阶1 周期解是轨道稳定的.

证明当h≤y*时，

记脉冲集

记相集

如图12，过A′作y=（1 -p）h的垂线，垂足为A1，记A1坐标为（xA1，（1 -p）h）.

图12 E*为结点时，系统（2）阶1 周期解的存在性Fig. 12 Existence of order-1 periodic solutions of system（2）for the node of E*

过A1的轨线L1交y=h于A2，脉冲后交y=（1 -p）h于A3，记A3坐标为（xA3，（1 -p）h），则A3为A1的后继点，且xA3＞xA1.于是，后继函数f（A1）=xA3-xA1＞0.

过B的轨线L2交y=h于B′，脉冲后交y=（1 -p）h于B1，坐标为（xB1，（1 -p）h），则B1为B的后继点，且xB1＜xB，于是，后继函数

由连续函数的介值定理，在点A1与B之间存在点H，使f（H）=0.H点对应的坐标为（xH，（1 -p）h）.过H的轨线交y=h后脉冲到H点，说明阶1 周期解存在.

用定理4.1 的方法可证得阶1 周期解的唯一性和稳定性.

情况2h＞y*.

因E*（x*，y*）是结点，故轨线至多经过若干次脉冲后趋于E*（x*，y*）.如图13.

图13 结点的轨线趋势Fig. 13 Trajectory tendency for the node

5 数值模拟及其生物意义

对脉冲系统（2）进行数值模拟

情形1 取b=1，a=0.4，c=0.1，δ =0.5，β =0.5，则系统的正平衡点E*是稳定的焦点，其中x*=0.5，y*=2.7.

1）取h=2.5，p=0.3，则h≤y*，脉冲系统（2）存在阶1 周期解，如图14.

图14 对h≤y*，脉冲系统（2）的相位图及时间序列Fig. 14 Phase portrait and time series of system（2）for h≤y*

其中，x（0）=0.893 5，y（0）=2.5.

2）取h=3.32，则h＞y*，存在p*，p=p*=0.475时脉冲系统（2）存在阶1 周期解，如图15.

图15 当p=p* =0.475 时，脉冲系统（2）的相位图及时间序列Fig. 15 Phase portrait and time series of system（2）for p=p* =0.475

其中，x（0）=0.5，y（0）=3.32.

3）取p=0.65，则p＞p*，脉冲系统（2）存在阶1 周期解，如图16.

图16 对p ＞p*，脉冲系统（2）的相位图及时间序列Fig. 16 Phase portrait and time series of system（2）for p ＞p*

其中，x（0）=0.87，y（0）=3.32.

4）取p=0.3，则p＜p*，轨线至多脉冲若干次最终趋向E*，如图17.其中，x（0）=0.85，y（0）=2.

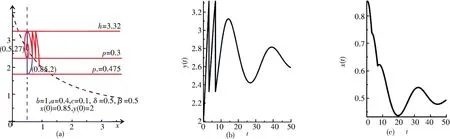
图17 对p ＜p*，脉冲系统（2）的相位图及时间序列Fig. 17 Phase portrait and time series of system（2）for p ＜p*

情形2 取b=0.5，a=1，c=1，δ =0.15，β =0.5系统的正平衡点E*是稳定的结点，其中x*=0.5，y*=1.

1）取h=0.9，p=0.3，则h≤y*，系统（2）存在唯一的阶1 周期解，如图18.

图18 对h≤y*，脉冲系统（2）的相位图及时间序列Fig. 18 Phase portrait and time series of system（2）for h≤y*

其中，x（0）=0.7，y（0）=0.9.

2）取h=1.2，p=0.4，则h＞y*.

3）系统（2）轨线至多脉冲若干次最终趋向E*，如图19.

图19 对h ＞y*，脉冲系统（2）的相位图及时间序列Fig. 19 Phase portrait and time series of system（2）for h ＞y*

其中，x（0）=1.3，y（0）=1.15.

4）系统（2）没有脉冲，轨线最终趋向E*，如图20.

图20 对h ＞y*，脉冲系统（2）的相位图及时间序列Fig. 20 Phase portrait and time series of system（2）for h ＞y*

其中，x（0）=0.6，y（0）=0.6.

6 结论及生物意义

1）无脉冲系统有全局渐进稳定的正平衡点E*（x*，y*），其中E*满足条件

2）周期T的长度由y=（1 -p）h与y=h的宽度λ决定，p越大，λ越大，阶1 周期解越长.用后继函数的方法获得系统阶1 周期解的存在性、唯一性和轨道渐近稳定性，只要h≤y*，脉冲系统（2）均存在唯一阶1 周期解且轨道稳定.特别地，当正平衡点E*是稳定的焦点时，存在p*，当p＞p*时，脉冲系统存在唯一阶1 周期解.脉冲系统的阶1 周期解是轨道稳定的.阶1 周期解的周期T随着p增大而增大，如图22.

结论表明：在稻田中插一些毛竹引诱成年螺集中附着产卵，然后对卵进行集中销毁，喷射茶麸水可有效防控福寿螺，茶麸水可通过脉冲控制喷射强度来控制杀螺的时间间隔.