一类含时滞和非线性扰动项的不确定随机微分大系统的稳定性
2021-01-03李树勇
易 玲, 李树勇
(四川师范大学 数学科学学院,四川 成都610066)
含时滞的不确定随机微分系统广泛应用于物理、化学、生物学、工程等领域,由于时滞和随机因素的影响,导致系统不稳定或震荡,因而,含时滞的不确定随机微分系统的稳定性分析受到学者们大量的关注,一系列的结果被建立[1-9].通常,学者们用Lyapunov 泛 函 法[1-5]、Lyapunov - Razumikhin法[6]或线性矩阵不等式法(LMIs)[7-9]研究含时滞的随机微分系统解的稳定性,然而Lyapunov泛函或函数构造较困难.因此,学者们致力于寻求其他的易于判别含时滞随机微分系统稳定性的技巧.最近,Wang 等[10]利用非负矩阵、随机卷积和不等式技巧研究了一类具有时滞的非线性随机偏微分方程的稳定性,建立了这个系统解的吸引域和稳定性的判别定理.受他们思想的启发,本文通过建立常数变易公式,利用非负矩阵性质和不等式技巧,研究一类含时滞和非线性扰动项的不确定随机微分大系统的吸引性和稳定性,得到判断这个系统吸引性和稳定性的充分条件,所得结果易于验证且没有要求非线性扰动项范数有界,扩大了稳定性的判别范围.
1 基本准备
本文中,Rn表示n维的欧式空间,R表示n维非负的欧式空间. ∀a∈Rn,定义‖·‖=I表示n×n维的单位矩阵,(Ω,F,P)是给定的完备概率空间,{Ft}t≥t0是(Ω,F,P)上给定的σ-代数流,满足通常条件.w(t)是定义在其上的一维实值布朗运动,E(·)表示期望.对τ >0和正整数m,Cm≜C([-τ,0],Rm)表示从[-τ,0]到Rm的连续函数空间,其上定义范数为‖φ‖τ=其中φ=(φ1,…,φm)T∈Cm.对p≥2,定义表示满足E‖ζ‖p<∞的Rm值F 可测的随机过程ζ 的集合,Cm)表示满足的Cm值F可测的随机过程 的集合.分别定义范数


本文考虑含有时滞和非线性扰动项的不确定随机微分大系统Σ,它由如下子系统Σi(i=1,2,…,N)组成:

定义1.3假设齐次泛函微分方程

其中,x∈Rm,L(t,xt)=A(t)x(t)+B(t)x(t-τ),A(t)和B(t)是m×m的连续矩阵函数.则称矩阵Φ(t-s)是齐次方程(5)的基本解矩阵是指Φ(t-s)满足

由文献[11]的定理3. 1,方程(5)的基本解矩阵存在.
引理1.1[12]对于如下随机微分系统

证明由(6)式,i=1,2,…,N,得
dΦi(t)=[Ai(t)Φi(t)+ Bi(t)Φi(t -τ)]dt.令ηi(t)=Φi(t)yi(t)(i=1,2,…,N),其中yi(t)满足
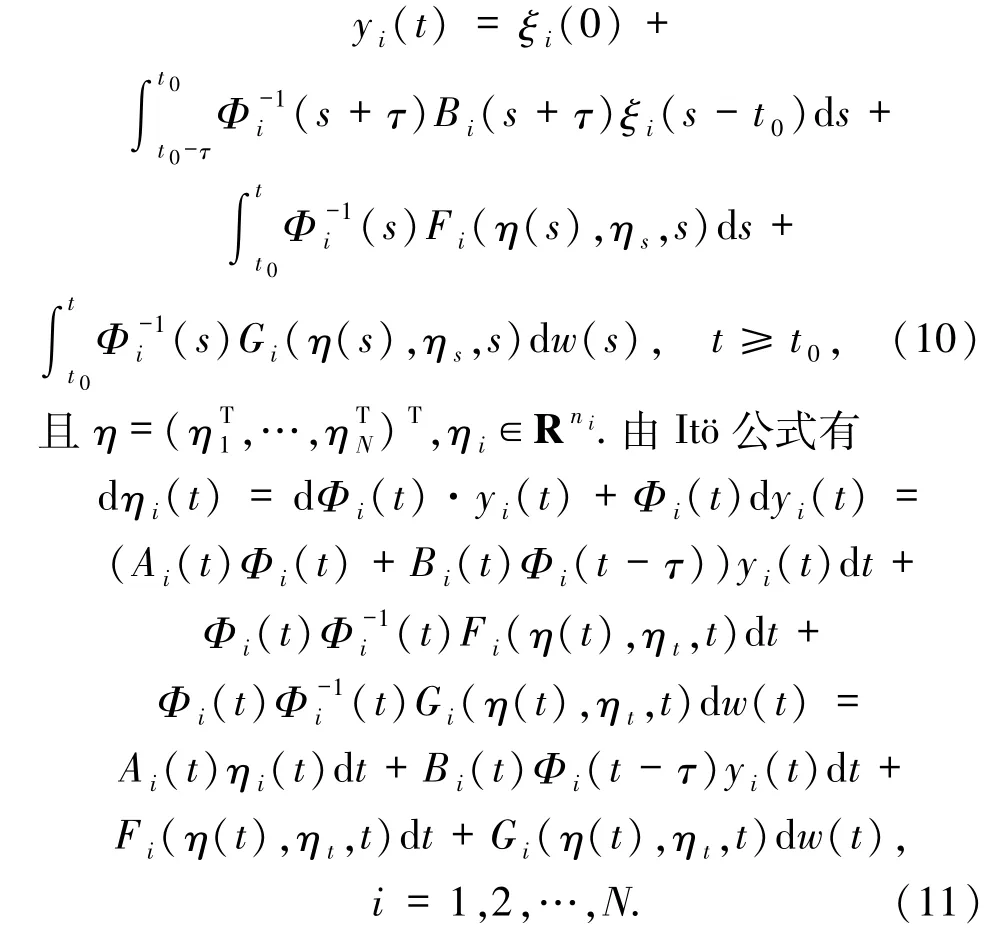
与系统Σ对比,只需要证明

事实上,由(6)式有
Φi(t -τ- s)=0,s∈[t -τ,t],所以

同理
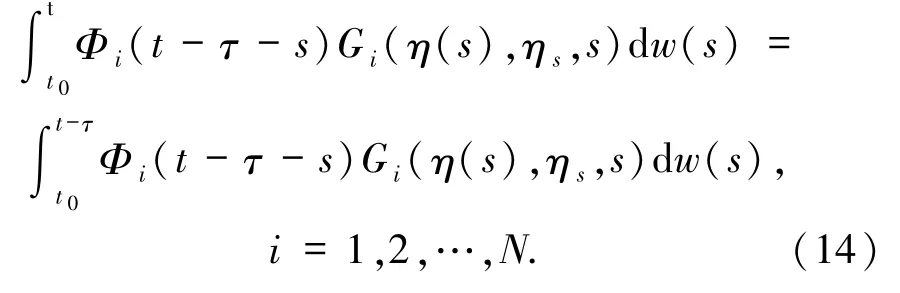
因此
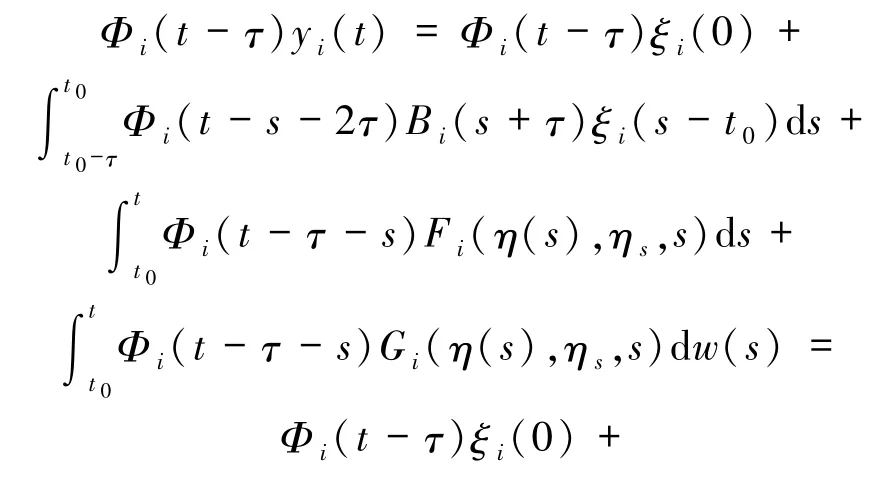
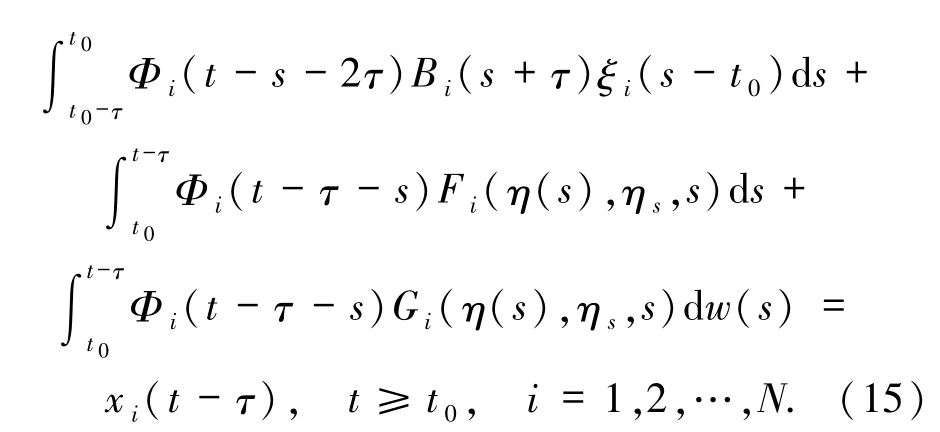
从而(12)式成立,即η(t)是系统Σ 的具有初始函数ξ的解.另一方面,由于系统Σ 的解唯一存在,所以x(t)=η(t),即(9)式成立.
2 主要结果
定理2.1对于系统Σ,假设:
(H1)存在向量函数H(φ)=(h1(φ),…,hN(φ))T和K(φ)=(k1(φ),…,kN(φ))T,且hi(φ),ki(φ):RN+→R+是连续单调不减的凹函数,使得

(H2)设Φi(t)(i=1,2,…,N)是齐次方程(8)的基本解矩阵,满足

并存在常数Mi≥1 和μi>0 使得

(H3)存在一个常向量z=(z1,…,zN)T≥0使得

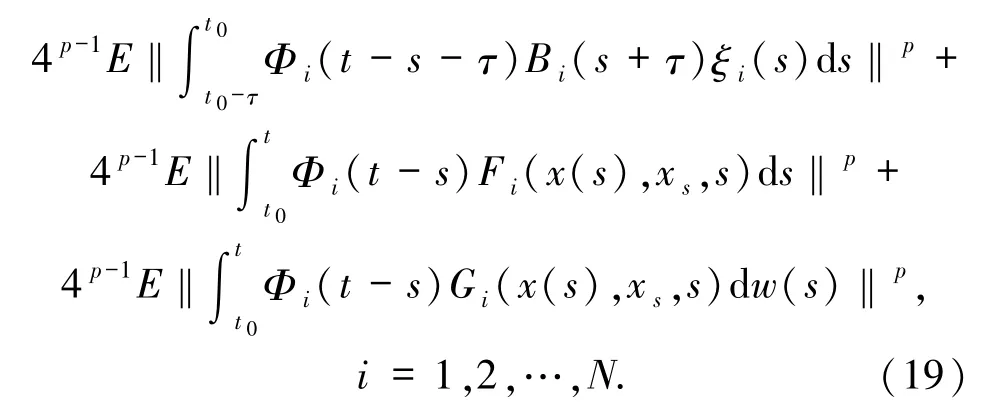
现在,对(19)式右边分别进行估计.首先,由条件(H2)有

再次,由条件(H1)和(H2)、BDG不等式[12]和Hölder不等式有
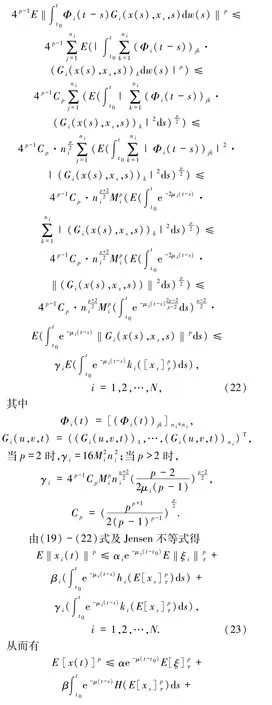

与(28)式矛盾.因此,(27)式成立.令ϵ→0,则(26)式成立.
定理2.2假设定理2.1 中所有条件成立.令向量函数

根据上极限的定义和(32)式,∀ϵ >0,∃T1>t0使得对任意的t≥T1,有
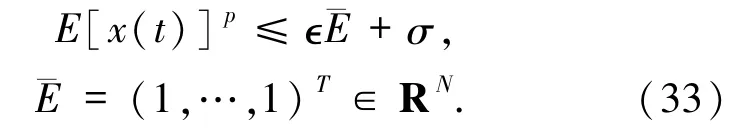
另一方面,由广义积分性质的定义,∃T2>t0使得

(35)式两边求上极限得

令ϵ→0+,则
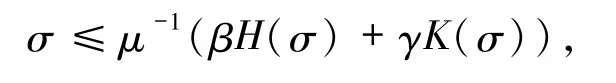
所以Ξ(σ)≥0,σ∈Ω0,即S是系统Σ 的p-阶矩吸引集.
由函数Ξ(y)的定义,易知集合


3 例子
例3.1考虑如下的一维时滞的随机不确定微分方程
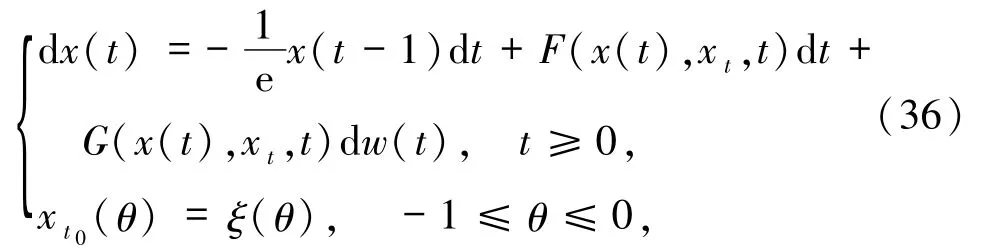
其中,xt(θ)=x(t+θ),-1≤θ≤0.
假设F和G满足

因为齐次确定方程


所以有Ξ(y)=(Ξ1(y),Ξ2(y))T,其中


