多段迭代制导对零窗口发射的适应性研究
2020-12-31吕建强王晋麟
吕建强,王晋麟,徐 帆
(北京航天自动控制研究所,北京,100854)
0 引 言
卫星发射窗口是指可供火箭发射的时间集合,包括发射日期和发射时刻[1]。从卫星轨道上划分,发射窗口定义为异面窗口和相位窗口[2],其中相位窗口主要受发射时刻和火箭飞行时间影响[3]。零窗口发射要求火箭不仅把卫星送入预定轨道,还必须满足相位要求。
发射窗口由卫星任务与星上设备要求所决定[1,4,5],在某些情况下,需要火箭具有零窗口发射能力,例如交会对接、探月任务等。长征七号运载火箭采用迭代制导实现了准确入轨[6],对零窗口发射要求具备一定的适应能力。长征七号是二级火箭,采用单级迭代制导方案,对于多级或者多飞行段的火箭,可以采用多段迭代制导方案,通过适当的设计,可以提升火箭对零窗口发射的适应性。
1 制导方法
理想情况下,运载火箭在指定时刻起飞,按照理论时间飞行即可满足入轨要求,但是由于各种原因,火箭并不能在指定时刻起飞,例如设计弹道时并不知道从点火到起飞的精确时间。实践中一般通过制导设计来克服起飞时间偏差问题。
运载火箭在大气层内飞行时,一般采用摄动制导。摄动制导需要事先计算标准弹道,克服飞行中各种干扰带来的偏差,而干扰是未知的,所以飞行时长是未知的,单纯的摄动制导难以适应零发射窗口的要求。
中国新一代火箭在大气层外飞行时,基本采用迭代制导方法[6],迭代制导是以最优控制原理为基础,通过在线计算入轨点,解析计算出飞行程序角[6],调整飞行轨迹,实现精确入轨。通过对入轨点的自适应调整,迭代制导可以满足一定条件下的零窗口发射要求。
迭代制导指令程序角cxφ 、ψcx,由式(1)计算得到[6,7]:
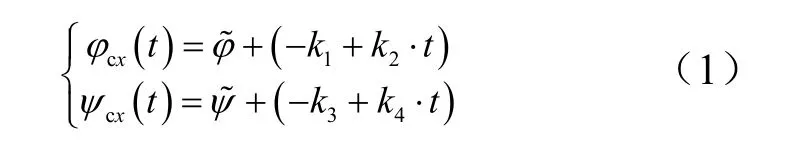
速度约束:
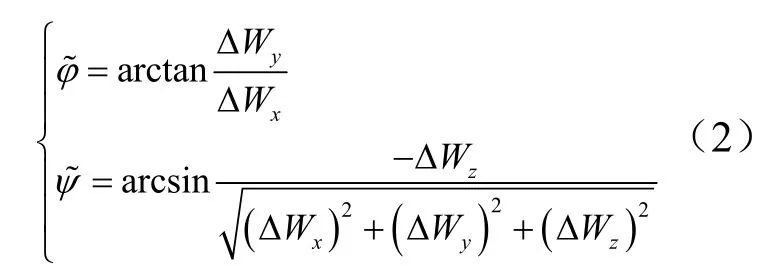
式中 Δ Wx, ΔWy,Δ Wz为发动机产生的速度增量在箭体系的分解。
位置约束:
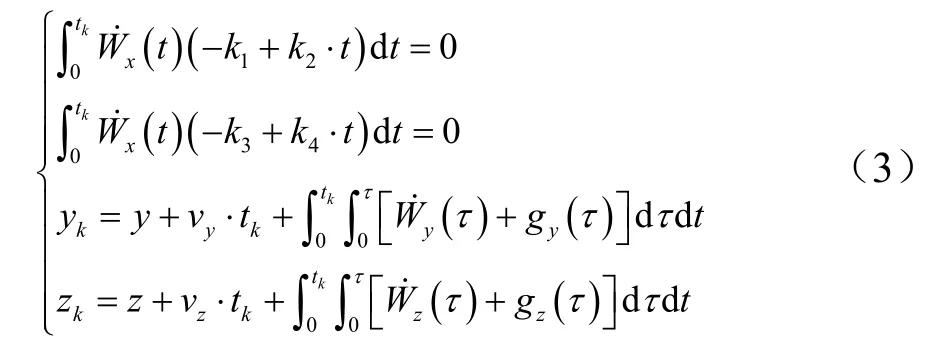
火箭飞行时控制6 个轨道根数 a , e, i , Ω ,ω ,τ 中的5 个参数,τ 由起飞时间保证,要控制的5 个量与时间相关的是Ω ,因此本文主要讨论多段迭代制导对升交点经度的控制。
2 单段迭代对零窗口的适应性
假设起飞时刻偏差是一个较小的时间,目标轨道的其它量不变。理论起飞协调世界时(Coordinated Universal Time,UTC)为t理论,实际起飞UTC 时刻为t实际,起飞时刻偏差为

地球自转角速度为ω,目标轨道的升交点经度为

3 多段迭代对零窗口的适应性
以3 段迭代制导的火箭为例,发射高轨卫星通常采用具有中间轨道的发射轨道[8],典型的一种弹道设计是飞行过程中具有停泊轨道和转移轨道[9],见图1。
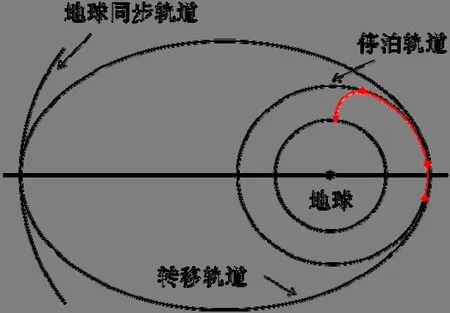
图1 飞行轨迹和轨道示意Fig.1 Illustration of Motion Trajectory and Orbit
多级火箭制导方法按照大气层内摄动制导,大气层外迭代制导设计,迭代制导二级飞行段、三级一次飞行段和三级二次飞行段,存在3 个不同的目标轨道。
如果存在起飞时间偏差 Δt ,则3 个目标轨道的升交点经度同时存在偏差,其中最终目标轨道的偏差如图2 所示。

图2 起飞时间偏差带来的轨道偏差Fig.2 Orbit Aberration Caused by Launch Time Deviation
针对零窗口的发射要求,设计方案为:
a)方案1:补偿二级飞行目标轨道、三级一次飞行目标轨道、三级二次飞行目标轨道;
b)方案2:补偿三级一次飞行目标轨道和三级二次飞行目标轨道;
c)方案3:补偿三级二次飞行目标轨道。
二级飞行目标轨道是一种亚轨道,考虑残骸落点要求、对入轨精度影响、安全性问题,二级不适合改变目标轨道参数,只有方案2 和方案3 可行,其中方案3 与单级迭代制导对零窗口适应性相同,假设起飞偏差为Δ1t ,方案2 和方案3 入轨精度仿真对比见表1。

表1 方案2 和方案3 的入轨精度对比Tab.1 Comparison of Accuracies of the Second Method and the Third Method
方案2 和方案3 区别在于飞行时间的差异,见表2。

表2 方案2 和方案3 的飞行时间对比Tab.2 Comparison of Flight Period of the Second Method and the Third Method
在入轨精度方面,两种方案都能满足要求,升交点经度偏差较不补偿时大大减小。其中方案3 的入轨精度比方案2 差一些,对于一定的起飞偏差仍然能够适应,且留有足够的余量,仅对三级二次的目标轨道参数补偿足够使用。
在飞行时间方面,方案2 的总飞行时间偏差小0.203 s,对应的三级推进剂约为3.9 kg。
综合考虑,可以根据任务需求从方案2 和方案3中选择任意一种。
对有限级的运载火箭来说,随着中间轨道数目的增加,轨道控制也变得更为复杂[8]。复杂带来了更多的控制维度,对于起飞延迟带来的升交点经度偏差,在一定条件下,可以通过调整滑行段时间来补偿。例如三级一次不补偿的情况下,停泊轨道的升交点经度发生变化,但停泊轨道必然有一个点可以满足升交点经度,改变滑行时间,仍然可以控制三级二次目标的升交点经度。
滑行段补偿机理是改变滑行时间,直接控制转移轨道面,弥补迭代制导对轨道面控制能力弱的问题,利用迭代制导轨道面内控制能力强,自行调整程序角适应各种变化。
假设起飞偏差为Δt2,对上述方案仿真的入轨精度见表3。

表3 调整滑行时间的入轨精度Tab.3 Accuracy of Changing Non-thrust Period
起飞延迟 Δt ,则滑行段减少 Δt 时间,可以完全补偿掉,仿真结果表明改变滑行时间可以减少起飞延迟带来的升交点偏差。
迭代制导升交点经度补偿和停泊轨道滑行时间调整综合使用,可以增加三级火箭对零窗口发射的适应能力。
设起飞延迟 Δ t,三级二次迭代制导补偿Δ t32,滑行时间补偿Δ thx,且满足 Δt =Δt32+Δ thx,仿真结果见表4、表5。

表4 不同补偿方案入轨精度对比Tab.4 Comparison of Accuracies of Different Methods
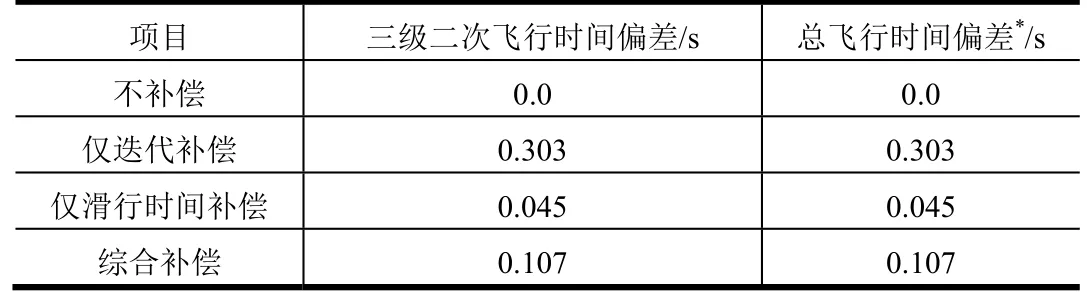
表5 不同补偿方案飞行时间对比Tab.5 Comparison of Flight Period of Different Methods
从仿真结果看,迭代补偿和滑行时间补偿互不影响,且对入轨精度影响程度相同,各项指标均可以满足要求。
只修改迭代制导目标,迭代制导会产生比较大的偏航程序角,如果目标改动,容易导致迭代失败;调整滑行时间,不会对三级二次之前的迭代制导产生影响,但是会影响三级二次关机时的纬度,如果调整太多,会导致三级二次难以入轨。所以对于零窗口发射的需求,可以将多段迭代制导调整目标轨道参数与改变滑行段时间长度的方法共同补偿起飞延迟带来的升交点经度偏差,这样可以在一定程度上增加制导对零窗口发射的适应性。
需要注意的是改变滑行时间会带来其它参数的变化,因而只能在小范围内变化。一般在弹道设计时,停泊轨道是用来满足转移轨道关机点的纬度的,滑行时间的改变,对纬度影响较大,需要考虑卫星用户对三级二次关机点纬度的要求,这一般靠弹道设计保证,制导设计只能在弹道设计基础上进行微调来适应干扰。
4 结束语
本文比较了多段迭代制导和单段迭代制导对零窗口发射要求的适应性,对于多段迭代制导的火箭,提出了将调整迭代制导目标轨道参数和控制滑行时间共同补偿起飞延迟带来的升交点经度偏差的方法,仿真结果证明了该方法的有效性。
