两种基于前馈神经网络的飞行器气动参数辨识方法
2020-12-31颜楚雄童轶男宋加洪
颜楚雄,童轶男,宋加洪
(北京航天长征飞行器设计研究所,北京,100076)
0 引 言
飞行器气动辨识在飞行器系统建模与仿真、飞行器控制系统设计以及故障诊断与分析等方面起着重要作用[1]。相较于风洞试验与数值计算方法,气动辨识方法能够获取飞行器真实飞行状态下的气动数据[2]。
常用的飞行器气动参数辨识方法包括极大似然法及其改进方法,如输出误差法和方程误差法等。这些方法需要建立飞行器的气动模型以及合理估计待辨识参数的初值。若模型建立不准确则会导致气动数据拟合结果不理想。若参数初值估计不合理,则容易导致陷入局部最小值[3]。
近年来,人工智能技术迅速发展,尤其是神经网络技术的日益成熟,给飞行器气动辨识提供了一种新的方法。神经网络有着以任意精度逼近任意函数的能力,因此可以避免气动建模过程,而且在气动参数估计过程中,不需要估计初值;在检验气动参数辨识结果时,不需重构飞行轨迹。国内外学者分别利用各类神经网络开展了气动辨识方面的研究,并且利用Delta法及其改进方法辨识各类气动参数[4~6]。但是这类方法属于有限差分方法,对气动参数的求解属于一种近似方法。
因此,本文建立3 层前馈神经网络,推导了神经网络输出参数对输入参数导数的表达式。提出利用前馈网络神经的导数特性[7],求解神经网络输出对输入导数的方法,从而求得相应气动参数。随后,针对某型飞行器纵向运动进行仿真,使用3 层前馈神经网络替代飞行器气动模型的建立过程,分别使用所推导的导数法与Delta 法辨识气动参数。最后,分析了测量噪声对辨识结果的影响。
1 前馈神经网络建立
神经网络能够从训练样本中进行学习,是一种自适应的学习方法。本文使用的为多层前馈神经网络,由三类层组成,分别为输入层、隐藏层和输出层[8],包含信号的正向传播与误差的反向传播两个过程组成。
1.1 信号的正向传播
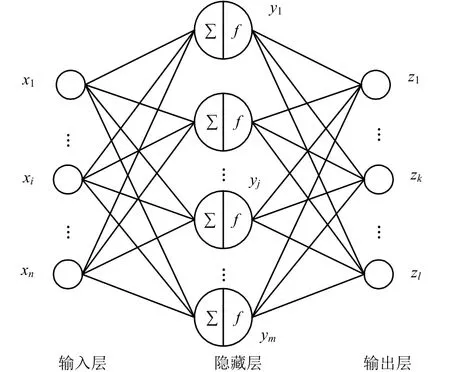
图1 神经网络示意Fig.1 Schematic of Neural Network
由图1 可知,神经网络可以看成一个非线性函数,其输入值与预测值可看作该函数的自变量与因变量。当输入节点数为n,输出节点数为l 时,神经网络就相当于从n 个自变量到l 个因变量的函数映射关系。
对于输出层z,其表达式为
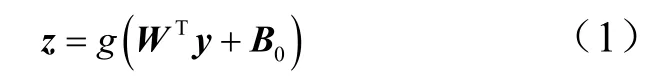
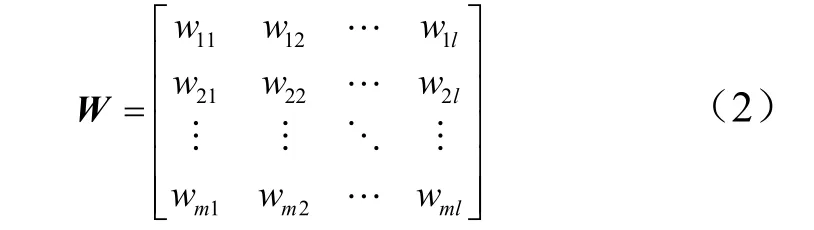
式 中 g ( · )为 激 活 函 数; y 为 隐 藏 层 神 经 元,W 为隐藏层到输出层的权值矩阵;wjk表示隐藏层第j 个神经元对输入层第k 个神经元之间的连接权值,则W 可以被写为
阈值 B0表达式为
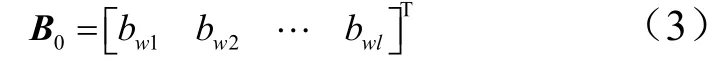
输出层y 可以写为

式 中 f ( · )为 激 活 函 数; x 为 输 入 层 神 经 元,V 为输入层到隐藏层的权值矩阵, vij表示输入层第i 个神经元对隐藏层第j 个神经元之间的连接权值,可写为
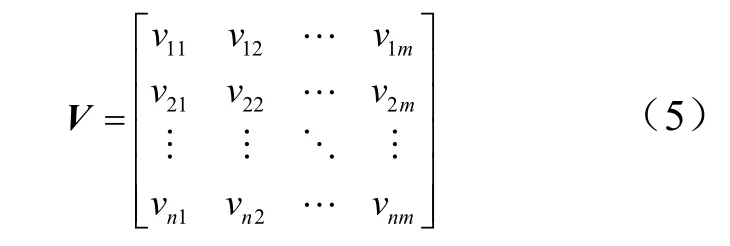
阈值1B 为
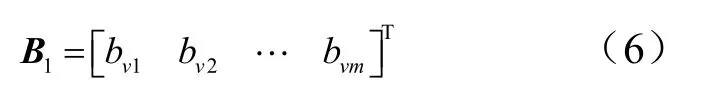
上述含有3 层的前馈神经网络,其表达式为
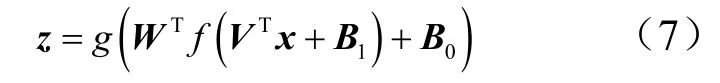
本文激活函数 f ( · )与 g ( · )分别选为tanh 函数与线性函数。 f ( · )可以表示为

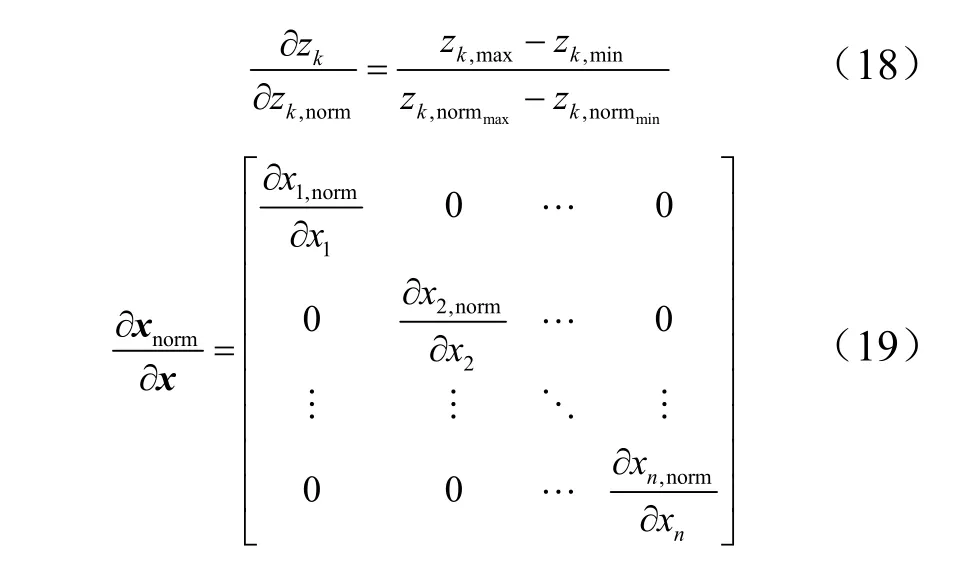
同时,为消除各维数据间的数量级差别,将输入与输出分别归一化,使得输入参数同等重要,避免数量级差别较大而造成网络预测误差较大,并且能够缩短训练时间。输入层的归一化方法为
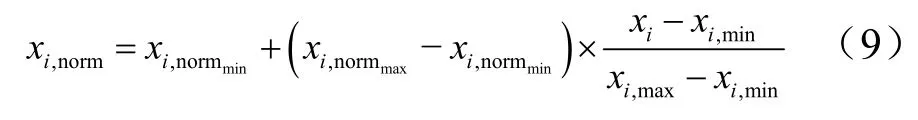
1.2 误差反向传播
误差的反向传播,即首先由输出层开始逐层计算各层神经元的输出误差,然后根据目标函数误差来调节各层的权值和阈值,使修改后的网络的最终输出能接近期望值。
本文神经网络目标函数采用均方误差和的指标衡量。对某一次训练例( xk,zk)而言,其均方误差为
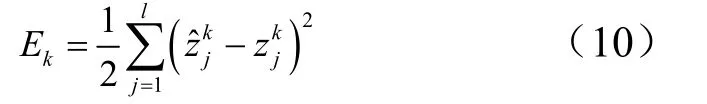
则所有训练例的总误差为
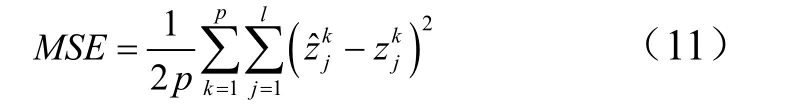
式中 p 为训练样本数。
本文神经网络的训练方法采用L-M 训练方法,L-M 算法是一种改进的高斯牛顿法[9],其形式如下:
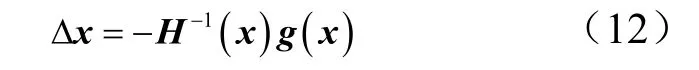
式中 H ( x )为函数的Hessian 矩阵; g ( x )为梯度。
此时,梯度与函数的Hessian 矩阵可以表示为
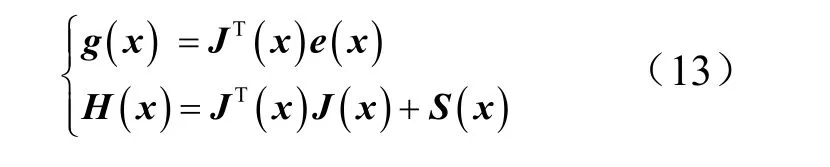
式中 J ( x )为函数的雅克比矩阵:

通过上述计算,Levenberg-Marquardt 算法通过对Hessian 矩阵的近似逼近,计算每一步的Δx 以更新x,其中Δx 为
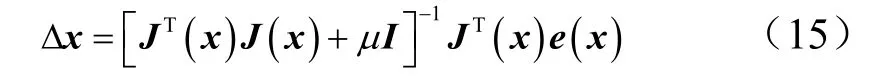
式中 μ 为比例系数;I 为单位矩阵。
应用该方法对所有数据重复进行反向误差传播算法,调节各层的权值和阈值,完成对神经网络的训练。
2 气动参数辨识方法
在训练结束后,所得到的神经网络就完成了对函数的映射。本文通过导数法与Delta 法两种方法对飞行器气动参数进行辨识。
2.1 导数法
借鉴类似于梯度下降策略中,求解输出误差对权值与阈值导数的思路,利用链式法则,求解神经网络输出对输入的导数,进而求得相应气动参数[7,10]。
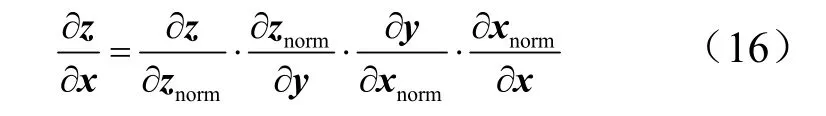
下面分别讨论上述各式的表达式。

其中,第k 项可以写为
其中,第i 项可以写为
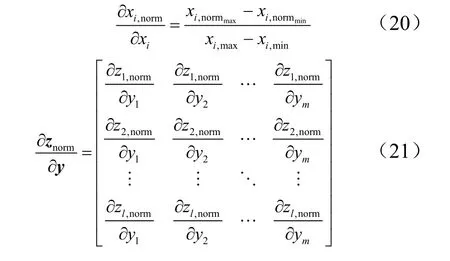
由于 g ( · )为线性函数,式(21)则可被简化为
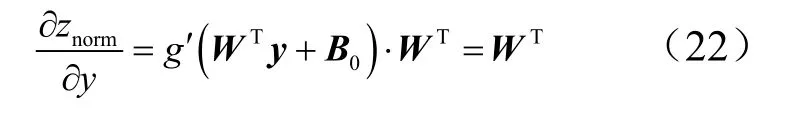
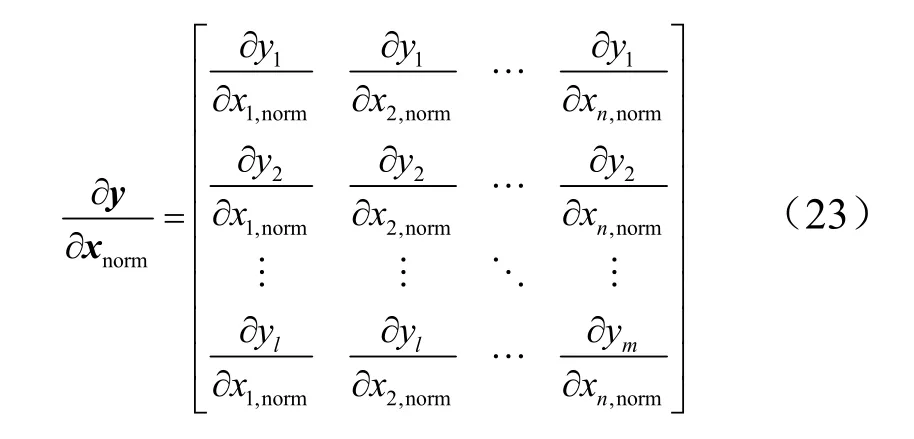
且
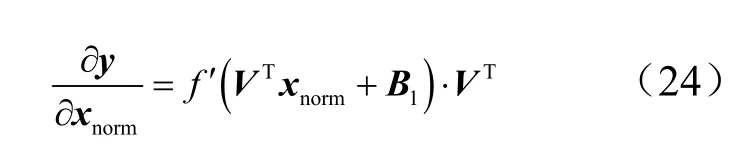
其中, f ′ ( x)根据式(4)可得:
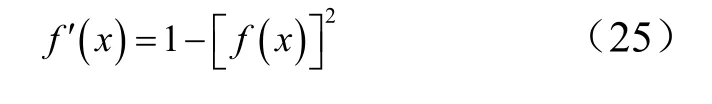
把式(17)、式(19)、式(22)以及式(24)代入式(16),即可通过导数法,完成前馈神经网络输出对输入的求导。当以气动系数作为神经网络的输出,以状态变量或者控制变量作为输入时,便可利用该方法对所有飞行试验数据求解气动参数。将所有数据点气动参数的平均值作为该参数的估计值并计算该参数的标准差。
2.2 Delta 法
Delta 法是一种有限差分方法,其思路为在输入层其他量不变的前提下,微小的改变某个状态变量或者控制变量将引起输出量的变化,两者的比值将是所求的气动导数[6]。对于力矩系数 CMα,利用训练好的神经网络,在其他输入不变的情况下,给α 分别增加或减少一个 αΔ ,得到α+αΔ 和α+αΔ 相对应的俯仰力矩与,则该系数可以写为

利用Delta 法,对一组飞行试验中所有数据点求取气动参数,将所有点的平均值作为参数的估计值,并计算该参数的标准差。
3 仿真结果分析
3.1 飞行仿真
本文针对某型飞行器纵向气动特性进行辨识。首先,建立飞行器动力学模型,仿真飞行数据由以下运动方程给出,其形式如下:

式中 Vx1,Vy1为体轴系上的速度分量;q 为俯仰角速率;ϑ 为俯仰角;m 为飞行器质量;g 为重力;S 为参考面积;Jz1为转动惯量;c 为参考长度; CA为轴向力系数;CN为法向力系数;CM为俯仰力矩系数;q∞为来流动压, q∞=ρ V2/2,其中:ρ 为大气密度;V 为飞行器飞行速度,
飞行器飞行总体参数如表1 所示。

表1 飞行器飞行参数Tab.1 Flight Parameter of Vehicle
轴向力系数CA,法向力系数CN与俯仰力矩系数CM的模型如下所示:
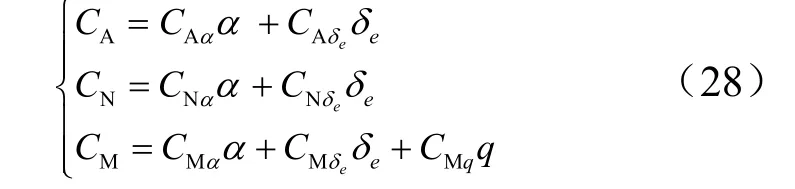
为了达到更好的辨识效果,仿真的激励信号采用偶极方波,其飞行状态如图2 所示。法向力系数 CN与俯仰力矩系数 CM的真值对于气动辨识而言是未知的,可由下式解算得:
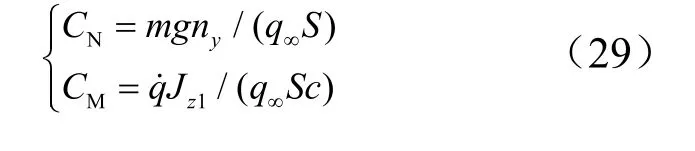
式中 ny为法向过载;为俯仰角加速度。
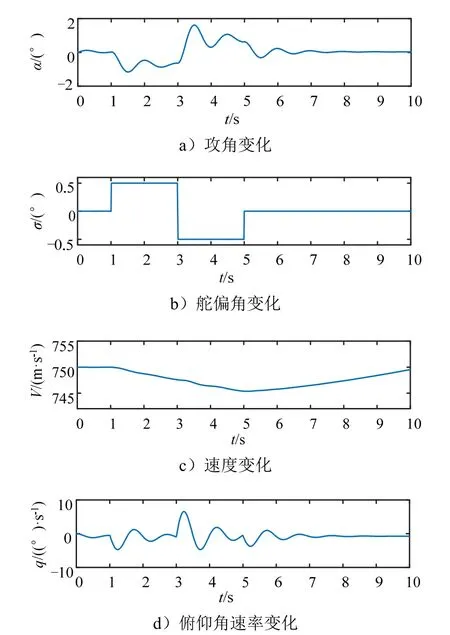
图2 飞行历程Fig.2 Flight Course
3.2 辨识结果
本文利用3.1 节得到的飞行仿真数据作为辨识原始数据,使用前馈神经网络方法对纵向气动特性进行辨识。以α、 δe及q 作为输入量,以法向力系数 CN与俯仰力矩系数 CM作为输出量训练神经网络。训练结束后,神经网络就形成了对气动模型的映射。随后,利用上文所述导数法和Delta 法求解气动参数。
图3 与图4 是利用神经网络辨识后的法向力系数CN及俯仰力矩系数 CM与测量值的对比情况。由图3、图4 可以看出辨识结果与真值拟合效果较好。
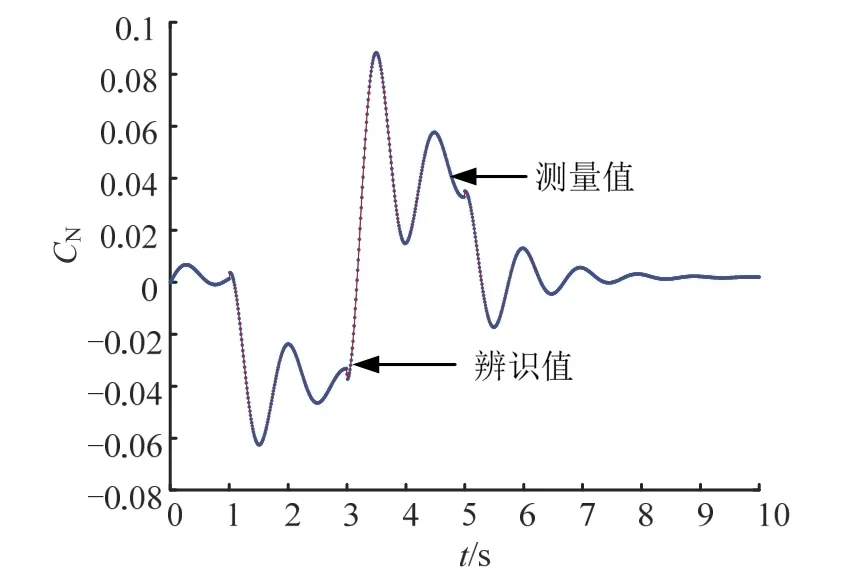
图3 法向力系数辨识结果Fig.3 The Identification Results of Normal Force
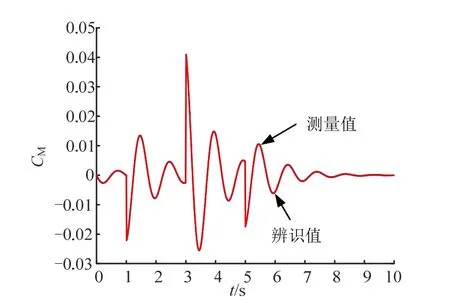
图4 俯仰力矩系数辨识结果Fig.4 The Identification Results of Pitching Moment
表2 为使用导数法和Delta法对气动参数进行辨识的结果。由表2 可知,在无噪声的情况,两种方法都能够很好的辨识出气动参数,结果与真值十分接近,同时,各项气动参数的标准差都较小,说明本文所提出的导数法与Delta 法都能够从飞行试验数据中辨识出气动参数,且具有较高可信度。
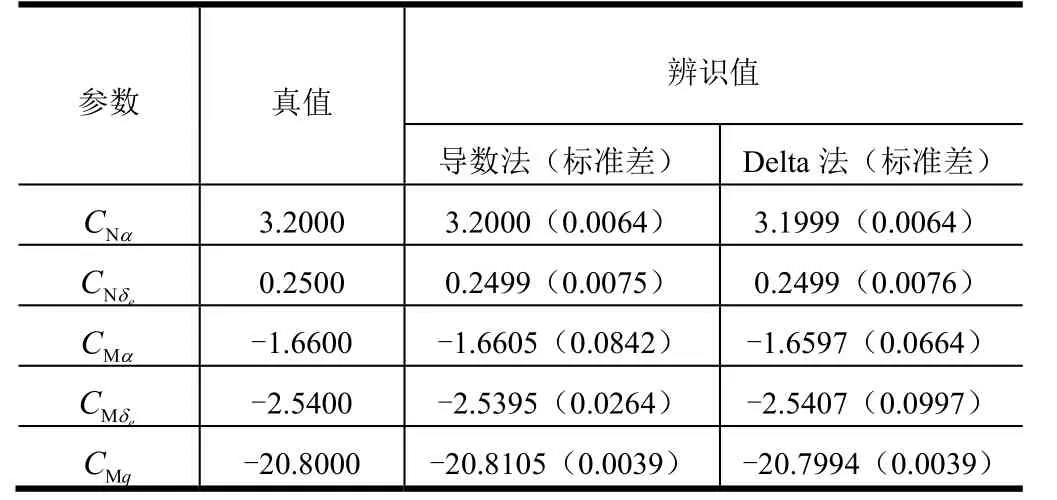
表2 无测量噪声时气动参数辨识结果Tab.2 The Results of Aerodynamic Parameter Identification with No Noise
为了分析测量噪声对参数辨识的影响,在仿真飞行数据中加入2%的白噪声。表3 为在测量噪声影响下的气动参数辨识结果,由表3 可知,该方法在一定测量噪声影响下,参数辨识方法依然能够较好地辨识出气动参数,具有一定的鲁棒性,但同时可以看出其标准差进一步增大,说明了测量噪声对辨识方法会增加其结果的不确定性。
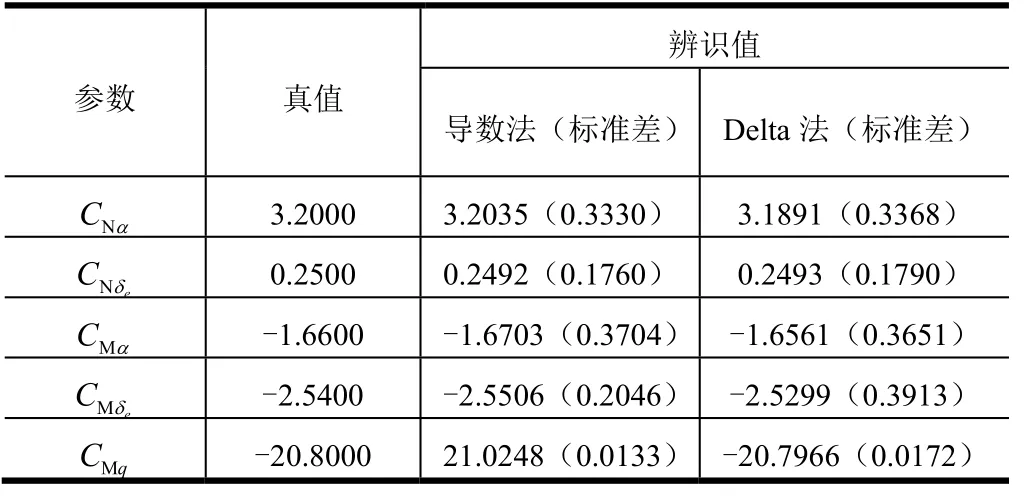
表3 有测量噪声时气动参数辨识结果Tab.3 The Results of Aerodynamic Parameter Identification with White Noise
对比表2 和表3 结果可以发现,相较于Delta 法,导数法所辨识出来的结果更接近于真值,而且其标准差也普遍较小。这是由于导数法利用了神经网络的导数特性,在求解中没有任何近似,所以得到了更精确的结果,而利用Delta 法对气动参数的求解是一种近似方法。因此,导数法在求解气动参数时更具优越性。
4 结束语
本文使用神经网络方法对飞行器法向力系数与俯仰力矩系数进行辨识。该方法避免气动模型的建立与辨识过程中的初值估计。利用前馈网络神经的导数特性,推导了求解法向力系数与俯仰力矩系数对各输入的导数法。利用该方法和Delta 法求解各气动参数,并得到相应标准差。通过与真值对较,神经网络辨识结果具有较好的拟合效果,求解的各气动参数接近真值,标准差较小。在测量噪声的影响下,上述方法具有一定的鲁棒性。通过比较,导数法比Delta 法在求解气动参数时更加接近真值,拥有更小的标准差。本文的方法还能够为今后对非线性气动特性的辨识提供一种可行的方法。
