紧凑型地波超视距雷达海杂波区目标检测影响因素研究

2020-12-30王祎鸣纪永刚

山东科学 2020年6期

王祎鸣，纪永刚

(1.自然资源部第一海洋研究所，山东青岛 266061；2.哈尔滨工业大学，黑龙江哈尔滨 150001；3.中国石油大学(华东)，山东青岛 266580)

目前，业务化运行的海上目标监测地波超视距雷达均为大型阵列式，依靠庞大的天线阵孔径，可以有效抑制照射范围以外的干扰与噪声(包括海杂波、射频干扰、大气噪声)，提高目标回波的信噪比和目标参数的估计精度。但大型阵列式地波超视距雷达系统接收天线阵尺寸大多在几百米至几千米，需占用大量稀缺的海岸线资源，限制了该系统的推广应用。因而小型海态探测类地波超视距雷达如SeaSonde、WERA及OSMAR等[1-3]的研究团队，开展了对目标探测功能的研发，同时目标探测类地波超视距雷达的研制方也进行了雷达系统的小型化设计。自然资源部第一海洋研究所联合哈尔滨工业大学、中国海洋大学以及中国石油大学等单位，研发了占地面积小、设备小型化和低功耗的紧凑型地波超视距雷达系统CORMS[4-7]。研究并发展紧凑型地波超视距雷达(high frequency surface wave radar,HFSWR)及其目标探测技术，对推广地波超视距雷达在海洋监视监测与海洋权益维护中的应用具有重要意义。

但是，地波超视距雷达回波中掺杂着大量的海杂波，严重影响了对船只目标的检测性能[8]，尤其是对海杂波区及其周边目标，海杂波对目标谱产生的遮盖作用进一步降低了对目标的检测能力，在系统紧凑型设计和小型化后，往往形成目标检测盲区[9]。为突破传统意义上的目标检测盲区，了解和掌握海杂波的产生机理及对回波的调制作用，以及其在雷达回波的时域、多普勒域以及联合域的特征[10-12]，从而区分海杂波与目标特性的不同，是后续处理的基础。目前，海杂波对目标检测的影响因素如海况、船只散射截面积(RCS)等已有研究[8-9]，但对海杂波区内及其临近目标检测的影响因素研究尚待开展。本文针对海杂波导致的目标检测盲区的特殊性，研究雷达积累时间的优化选取以及海杂波区目标与海杂波的关联关系，并结合紧凑型地波超视距雷达CORMS实测数据分析两者的雷达回波特性差异，为加深对海杂波特有规律的认识，实现海杂波区的目标检测提供依据。

1 紧凑型地波超视距雷达及信号积累时间分析

1.1 紧凑型地波超视距雷达系统

以自然资源部第一海洋研究所主持研制的紧凑型地波超视距雷达系统CORMS为例，该系统由单极子双鞭发射天线、偶极子接收天线、全固态发射机以及接收和信号处理机组成，系统实物见图1。雷达系统采用一发多收体制，各子系统采用紧凑化设计。在雷达发射端采用低功率固态发射机和双鞭天线，通过双天线实现端射的方式在空间形成发射方向图，增强辐射功率，提高探测距离和指向性。在接收端采用无需地网的小型化偶极子天线阵列和全数字化接收和信号处理机，降低天线阵占地面积。

图1 紧凑型地波超视距雷达系统CORMS

CORMS雷达采用线性调频中断连续波信号形式，系统参数：中心频率为4.7 MHz，带宽为60 kHz，扫描周期为0.123 s，平均功率为200 W。

1.2 信号积累时间分析

图2为地波超视距雷达检测海面目标的示意图，其中距离雷达R的船只目标以航速v由A点航行至B点，船只航向与雷达径向的夹角为θ0，目标方位变化量为Δθ。地波超视距雷达检测目标过程中，通过相干积累增强船只目标的信杂噪比，在保持目标为给定的雷达距离分辨率ΔR内且不受距离走动或多普勒拖尾[13]的情况下，适当延长积累时间有利于目标的检测。

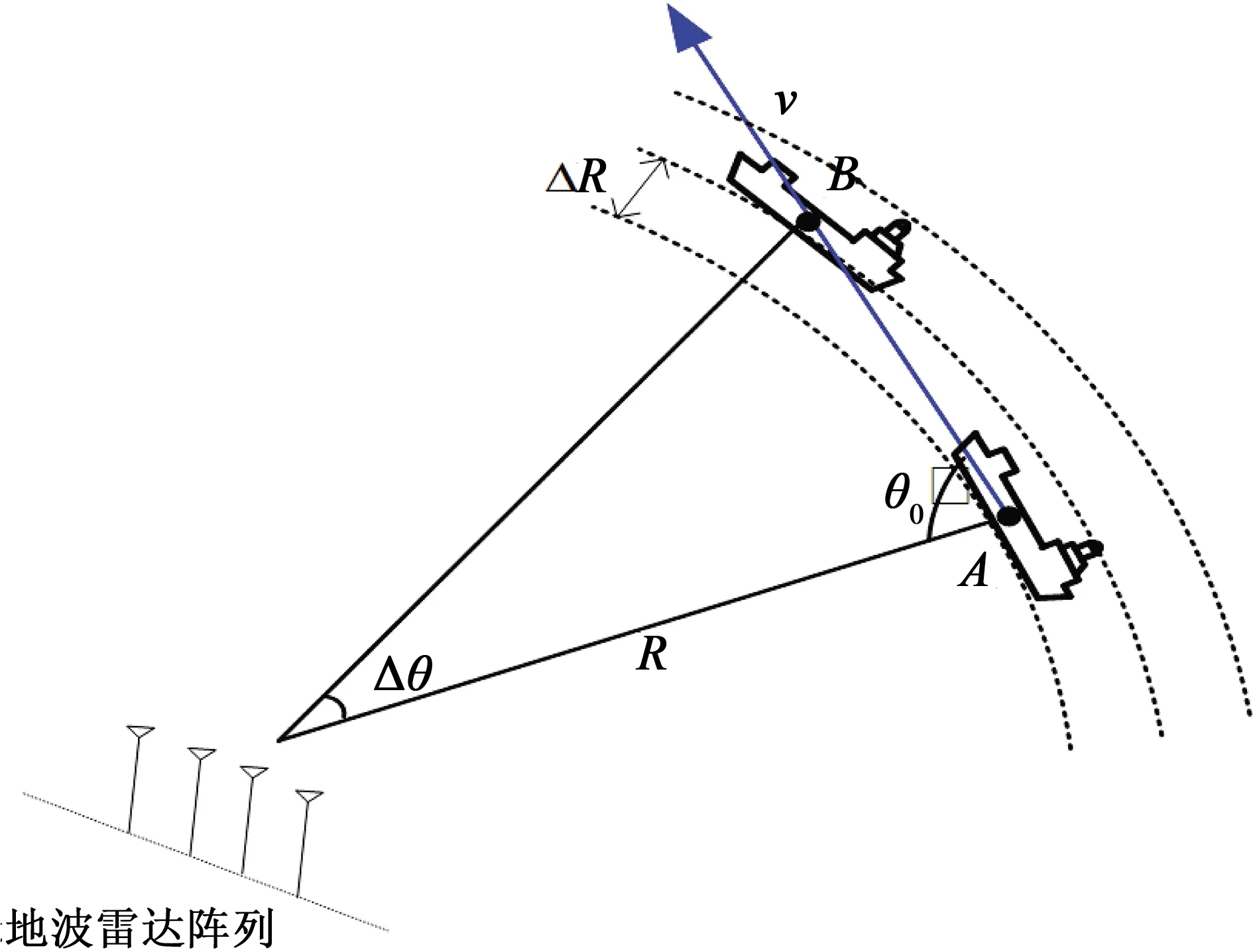
图2 地波超视距雷达检测航行船只示意图

为避免距离走动和加剧多普勒拖尾效应，雷达的积累时间受到船只航速、航向以及雷达距离分辨率的约束。该积累时间T与距离分辨率(或雷达带宽)及船只航速航向的关系为

T=ΔR/(vcosθ0)=C/(2Bvcosθ0)，

(1)

其中，C为光速，B为雷达带宽，vcosθ0为径向速度。

结合公式(1)，分别取雷达带宽30、60和100 kHz，以及目标径向速度5～40 kn，得到雷达最大可积累时间的变化规律(图3)。可见，随着雷达带宽的增加，径向速度落入海杂波区(12～15 kn)的目标最大积累时间由13.9 min降为4.1 min，海杂波区外高速目标最大积累时间由4.17 min降为1.2 min，可得平均积累时间由12.4 min降为3.7 min。但是，探测条件尚有很多不可控因素，如目标机动、散射截面变化、海浪散射变化等，且海杂波区内和海杂波区外目标的可积累时间也有所不同。因此，上述分析为相干积累时间的拟定划定了最大的取值范围。实际应用中，由于海杂波的时间相关性通常小于80 s，因此在兼顾整体雷达探测结果的前提下，平均积累时间保证了各种航速的目标相对海杂波均能得到更好的积累。以CORMS带宽为例，积累时间取5 min。

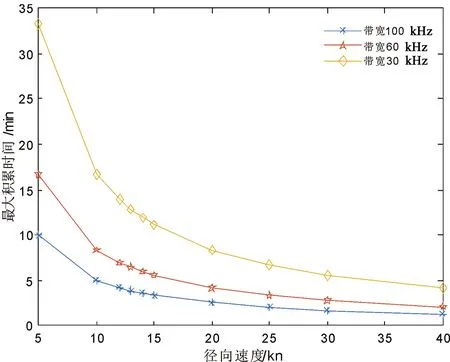
图3 目标最大积累时间与径向速度的关系

2 目标与海杂波区的关联分析

2.1 目标航速航向与海杂波区的关联分析

在目标方位与雷达径向一致时，两者方位夹角为0°，此时船只航行速度即为相对雷达的径向速度。目标在雷达回波距离-多普勒谱中表现为点状形式，其中回波距离为目标到雷达的直线距离，多普勒为目标径向速度导致的多普勒偏移。目标航速航向的改变将导致其径向速度vr随距离以及径向夹角产生相应的变化，表示为

vr=vcosθ0。

(2)

不同的目标径向速度又决定了其回波能否落入海杂波区，图4给出了目标径向速度与航行状态的关联图，图中虚线为雷达中心频率为4.7 MHz时的海杂波上下界。可见随径向夹角的增大，目标径向速度逐渐降低，其中目标航速越高，航向的变化越易导致其落入或驶出海杂波区。海杂波多普勒区对应的径向速度为12～15 kn，表明航行速度大于12 kn的目标均存在落入海杂波区域内的可能性，以15 kn左右航行的目标落入海杂波区的可能性最大，由表1可见径向夹角覆盖量为38°。随着目标航行速度的增大，目标落入海杂波区所对应的径向夹角范围减小。另外，由海杂波Bragg频率计算公式[2]可以推知，随着雷达频率的升高，海杂波区将下移导致落入该区的目标速度最小值降低，增加船只落入海杂波区的概率。

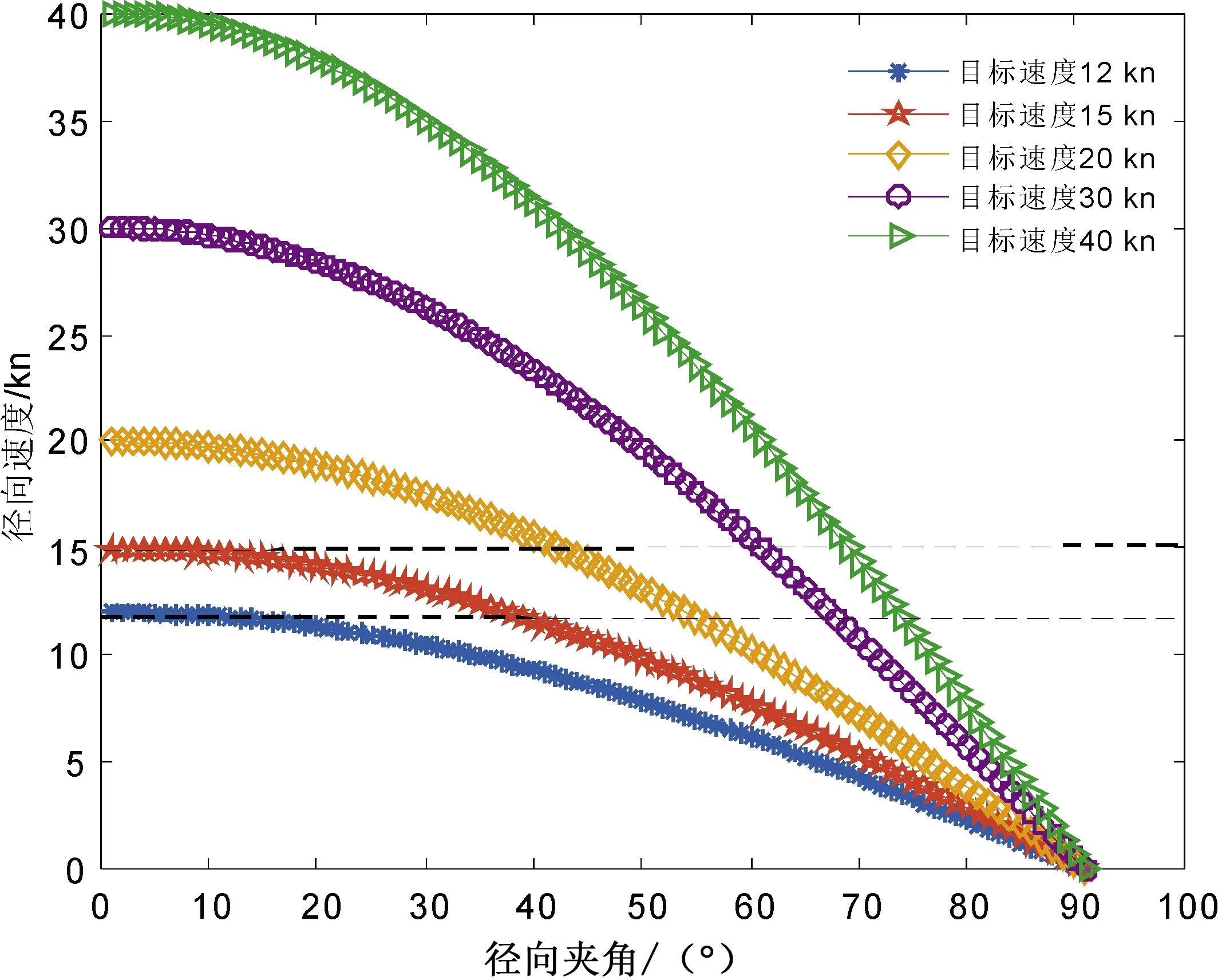
图4 目标径向速度与径向夹角的关系

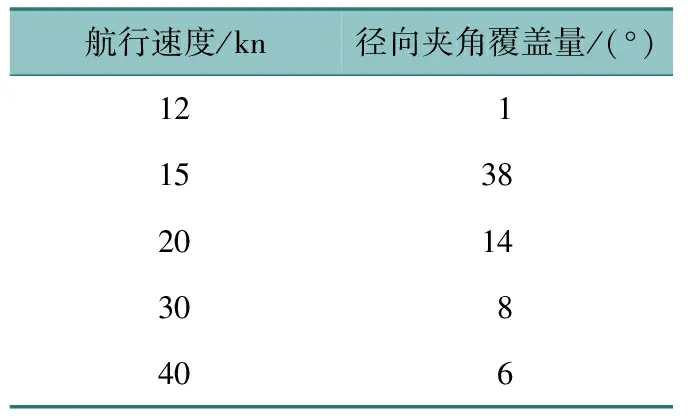
表1 海杂波区目标航行速度及对应的径向夹角覆盖量

2.2 海杂波区非机动目标驻留时间分析

在满足目标径向速度落入海杂波区的前提下，海杂波区非机动目标驻留时间与目标距离，方位变化量及航速、航向的对应关系可表示为

t=Rsin Δθ/{vsin(Δθ+θ0)}，

(3)

其中，θ0=arccos(vr/v)为满足径向速度为vr的目标航向。

以目标径向速度为12 kn为例，目标开始落入海杂波区，图5给出了其方位变化为1°且航向保持不变时，目标距离、速度与其在海杂波区驻留时间的关系。在近距离，目标在海杂波区驻留时间可小于4 min，随着目标与雷达的距离增大，其驻留时间逐渐增加，而随航速的增大目标潜在驻留时间降低。以距雷达150 km的目标为例，航速为13 kn的船只在海杂波区驻留时间最长，可达16.75 min，而30 kn或40 kn航速的船只目标驻留时间最短，约2～3 min。航速为15 kn和20 kn的船只在海杂波区驻留的时间至少为9.50 min和5.38 min。在远距离尤其是以13～15 kn速度非机动航行的船只，在雷达的积累时间内，难以驶出海杂波区。而从式(3)以及目标径向速度落入海杂波区的前提条件可得，非机动目标方位变化增加后，其在海杂波区内的驻留时间将进一步增加。

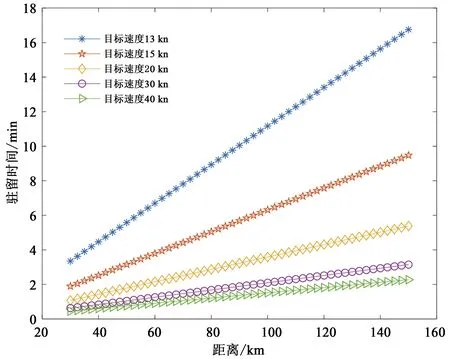
图5 海杂波区非机动目标驻留时间

3 实测数据分析

结合紧凑型地波超视距雷达的实测数据分析影响因素，图6给出了海杂波及目标多维联合分析结果。图6(a)为5 min信号积累后形成的距离-多普勒谱，可见海杂波为条带形状，几乎遍布所有距离单元，符合海杂波的大范围面目标特征，而目标表现为点状目标形式，并且海杂波条带中的目标难以直接解译。因此在后续分析中，将同步船只自动识别信息AIS投影[14]到CORMS坐标，用虚线表示，而海杂波区用实线框出。图6(b)为海杂波区的回波时频分布，由AIS信息可知该海杂波区内的船只目标航速、航向相对稳定，其径向速度介于12～13 kn，至少15 min难以驶出海杂波区，符合前述理论分析的结果，在此期间无法通过时频分析的检测方法发现。图6(c)为海杂波区的目标时间-距离分布，可见与海杂波多普勒重合的目标(径向速度12.39 kn)，其在时间-距离上与海杂波重合，在30 min或者更长时间内难以显现。然而，从图6(d)海杂波区目标的时间-空间分布可见，目标所在海杂波区的空间分布在时间维相对于雷达积累滑窗时间(1 min)不具有长时持续性。通过图6(e)～6(f)海杂波区外目标和无目标海杂波的时空分布表明，海杂波与目标在时空维具有较为明显差异，该差异可以由目标的航行特点和海浪传播的往复性解释。但当目标和海杂波在频率和距离上重合时，由于紧凑型地波超视距雷达的宽波束特点，两者回波方位如在同一宽波束内，则难以区分，需发展有效的波束内滤波方法提高海杂波区内目标的检测能力。

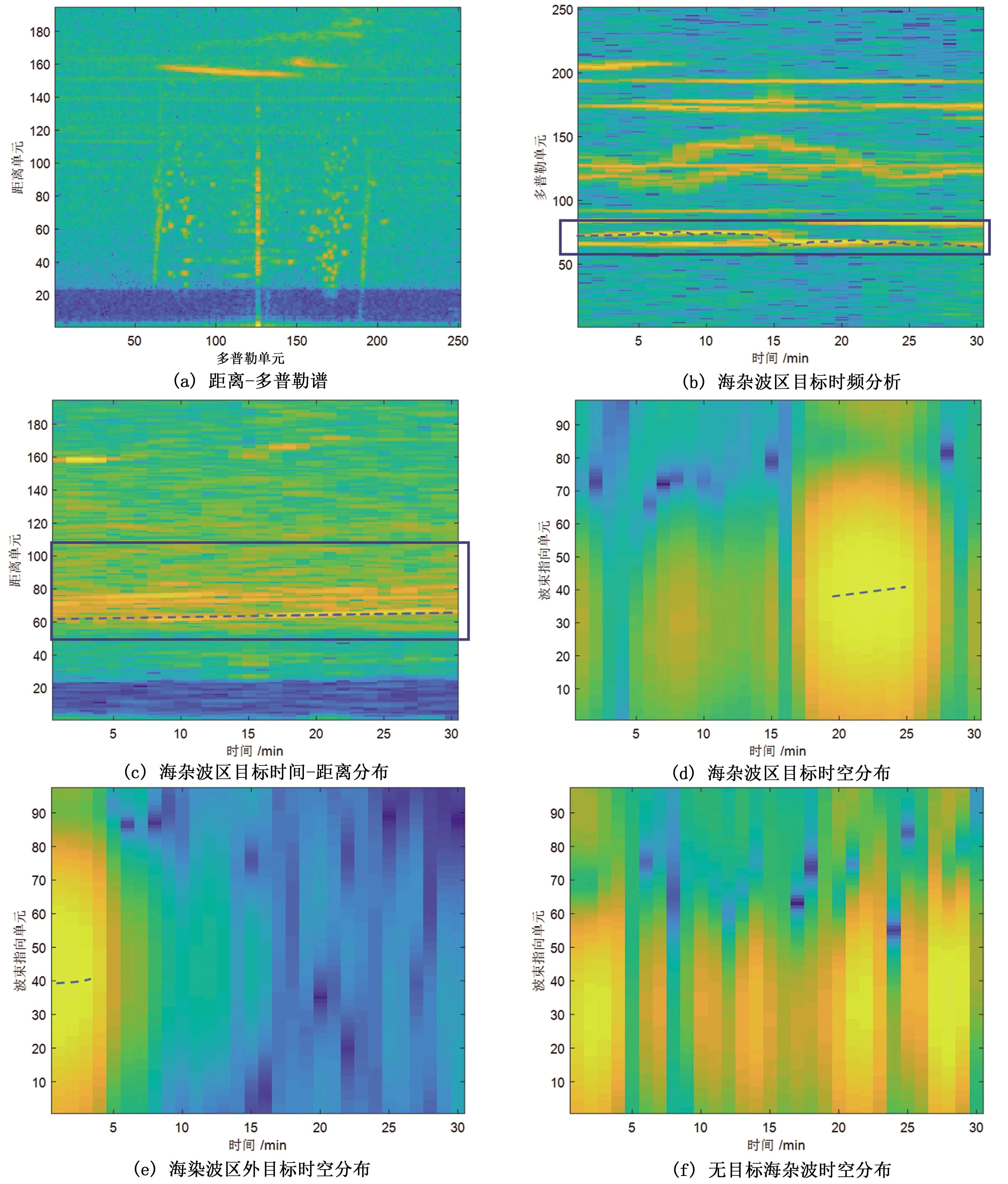
图6 海杂波及目标多维联合分析

另外，传统地波超视距雷达利用海水对垂直极化的高频电磁波衰减少的特点，均采用垂直极化发射-垂直极化接收的形式。但如在CORMS雷达接收端增加水平极化接收通道，可利用电离层杂波的极化通道差异显著提高电离层干扰的抑制性能。而海杂波和目标间的极化特性是否存在差异还没有理论证明，在此从实测数据统计方面加以讨论。极化域信息体现在不同极化通道之间的幅度和相位关系，即极化角和极化角相差，定义为[15]

γ=tg-1|xV(t)|/|xH(t)|，

(4)

η=arg(xV(t))-arg(xH(t))，

(5)

其中，xV(t)和xH(t)分别代表垂直极化和水平极化信号, arg(…)代表信号相位。

(2)若CP(a)＞1,则P∗(G)的连通分支个数为k(P∗(G))=s1(P)-s1(Φ(P))+1.

图7及图8分别给出了垂直极化、水平极化接收的回波距离-多普勒谱和相应的极化角及极化相差谱。图7中横向条带为电离层干扰，可以发现垂直极化距离-多普勒谱中海杂波和目标回波较强，而水平极化距离-多普勒谱中电离层干扰更强。表明海杂波和目标与电离层干扰的极化角具有较明显的区别，而极化相差尚难以直接解译出明显的不同，相关差异需通过统计量化体现。在此，通过对电离层干扰、海杂波以及目标的极化角和极化相差分布等极化特性进行分析。从图8极化角概率密度统计分布可见，电离层干扰的极化角主要集中在14°～50°，目标的极化角位于67°～84°且以79°左右居多，海杂波的极化角处于78°～86°且以82°左右为主。由极化相差概率密度分布可得，电离层干扰的极化相差主要集中在153°～228°，海杂波的极化相差位于35°～143°，目标的极化相差处于110°～274°。

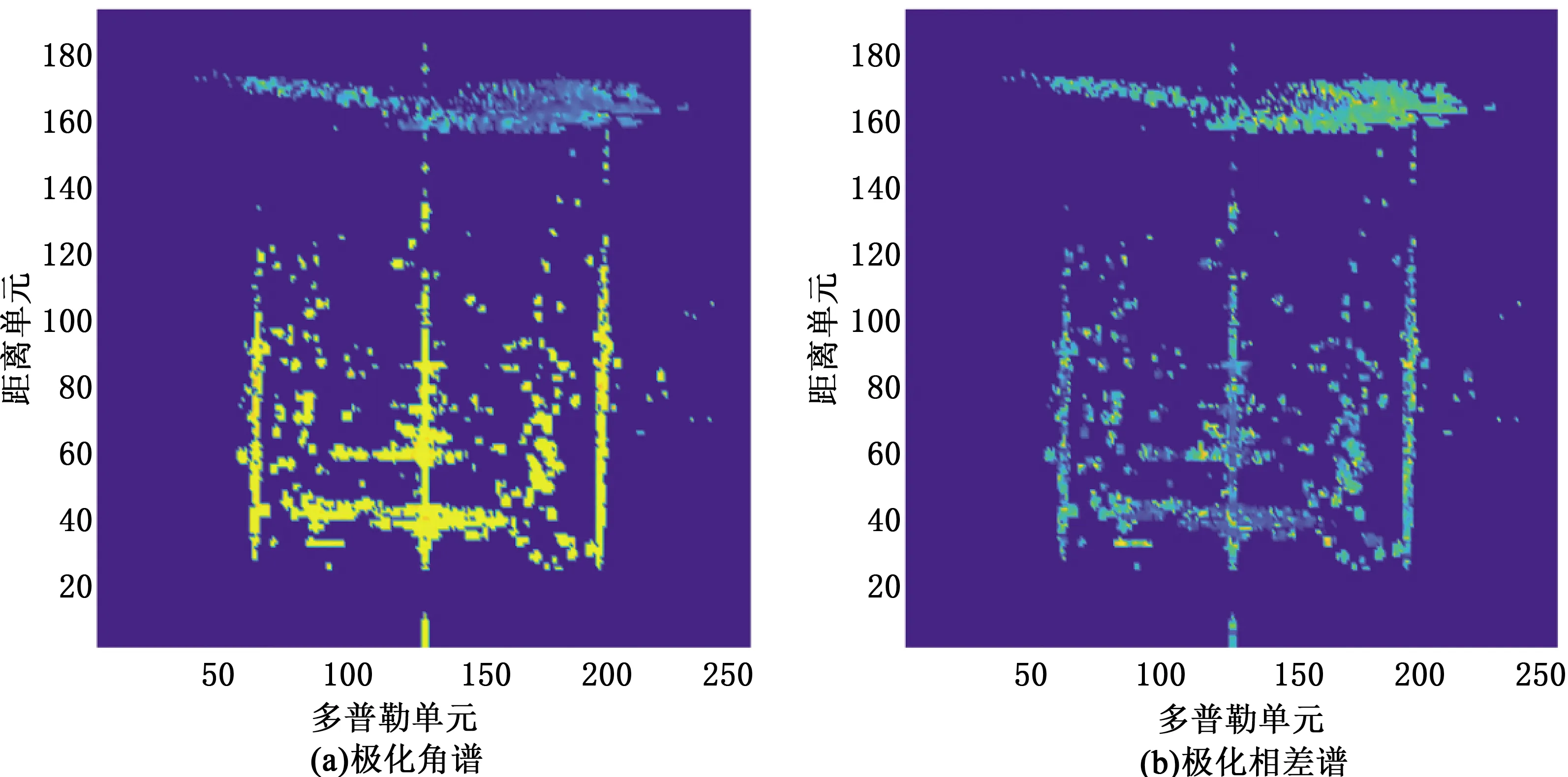
图7 极化角及极化相差谱

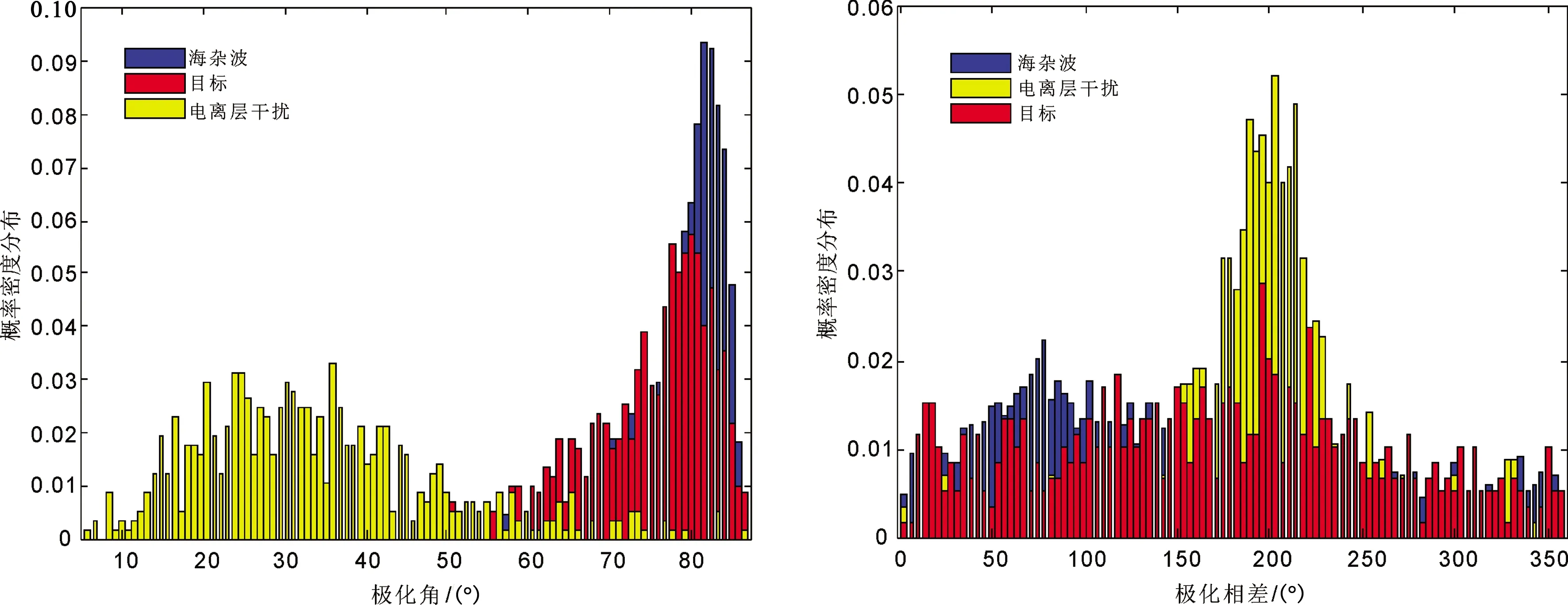
图8 极化角及相差概率密度分布

综合统计结果，海杂波与目标的极化角集中分布于80°左右，而电离层干扰的极化角基本上分布于20°～40°。海杂波与电离层干扰的极化相差分布相对集中，海杂波的极化相差位于30°～150°，电离层干扰为180°～230°，目标的极化相差分布相对分散，但在150°～230°居多。因此可见，目标和海杂波的极化角分布较为一致，两者与电离层干扰的极化角分布具有明显的界限。目标与电离层的极化相差分布具有较大的重合率，两者与海杂波的极化相差分布存在差异。