磷脂分子POPE的浮动电荷分子力场

宫利东, 赵力傧, 田 博, 杨忠志

(辽宁师范大学 化学化工学院，辽宁 大连 116029)

生物膜是细胞的重要组成成分,它作为细胞内和细胞外环境之间的屏障,提供专门的物理环境实现物质转运和信号传导,这些功能需要动态的流体环境,允许膜蛋白的旋转和平移扩散[1]. 细胞膜主要由磷脂构成,在原子和分子水平上理解磷脂双层的结构和动态特性是至关重要的[2-3].对于脂质双层的研究已有近百年的历史[4],主要实验技术有量热法(用于研究膜相行为)、荧光共振能量转移(FRET)、原子力显微镜(AFM)、核磁共振(NMR)、小角中子散射(SANS)、小角X射线散射(SAXS)、准弹性中子散射(QENS)和质谱等.随着计算机技术的迅速发展,分子动力学模拟已被广泛应用于探讨各种复杂体系的结构和性质,与实验技术相比,分子动力学模拟能够得到体系的原子级别的详细结构信息以及实验中难以捕获的微观细节.但其计算的成败很大程度上取决于力场的适用性、计算速度的快慢和计算方法的正确性.大多数的脂质力场采用固定电荷模型处理静电相互作用,比如AMBER[5]、CHARMM[6]以及OPLS-AA[7]和GROMOS[8]等力场.虽然固定电荷力场的计算成本相对较低,可以对较大体系进行长时间尺度模拟,但忽略了极化效应[9].由于磷脂分子的特殊结构,其嵌入式通过膜的外部和内部的环境是不同的,需要明确考虑极化作用[10].与传统力场相比,可极化力场模型可以表现体系的电荷分布或偶极矩等随环境和结构的改变而发生的相应变化,因此，建立磷脂分子的可极化力场近年来受到关注.目前，主要有3种可极化模型:诱导偶极模型[9-11]、Drude谐振子模型[1,10,12-13]和浮动电荷模型[14-17].李国辉等人报道了基于诱导偶极模型的AMOEBA力场、磷脂双层的1,2-二油酰基-磷酸胆碱(DOPC)、1-棕榈酰-2-油酰基-磷脂酰乙醇胺(POPE)、1-棕榈酰-2-油酰基-sn-磷脂酰胆碱(POPC)和1,2-二肉豆蔻酰基-sn-磷脂酰胆碱(DMPC)的可极化力场[9,18];Roux课题组[1,13]开发了1,2-二棕榈酰基-sn-甘油-3-磷酸胆碱(DPPC)、二月桂酰磷脂酰胆碱(DLPC)、二棕榈酰磷脂酰乙醇胺(DPPE)和1,2-二油酰基-sn-甘油基-3-磷酸乙醇胺(DOPE)、DMPC、POPE、POPC、DOPC等多种饱和及不饱和的两性磷脂分子体系的Drude可极化力场.

在密度泛函理论下的电负性均衡方法的基础上,杨忠志等创建和发展了原子-键电负性均衡浮动电荷分子力场方法(ABEEMσπ/MM),在对纯水、有机分子与聚合物、电解质溶液、核酸以及多肽蛋白质等体系的研究中,均获得了优于传统力场的结果[17].在本课题组之前建立的DPPC分子的ABEEMσπ/MM力场的基础上[19],继续开展对POPE的研究,为建立广泛适用于磷脂体系ABEEMσπ/MM力场打下基础.

1 理论和计算方法

1.1 计算方法

量子化学计算采用Gaussian 09[20]程序.将POPE分子的极性头部拆分为乙基三甲基铵(ETMA)、乙酸甲酯(MAS)、磷酸二甲酯(DMP)等小分子片段,选用MP2/6-31G*水平对中性和带正电的片段进行结构优化,而对于带负电的片段使用MP2/6-31+G(d)方法.对于POPE分子,为节省计算量,选用M062X泛函.其中,极性头部和尾部烃链分布选用6-31++G(d,p)和6-31G(d)基组进行结构优化和频率计算.对于电荷分布的计算,基于本课题组之前的研究[16],应用较大基组会高估两原子间极化作用,采用HF/STO-3G的方法.

1.2 POPE的ABEEMσπ/MM浮动电荷势能函数

根据ABEEMσπ/MM模型,构建了POPE分子的浮动电荷势能函数:

(1)

前2项分别为磷脂分子的键长伸缩和键角的弯曲振动势能,采用谐振子势能函数形式;第3项为二面角的扭转振动势能,采用Fourier级数形式;第4项为非共面二面角势能;第5项为范德华相互作用势,采用Lennard-Jones12-6形式;最后1项为静电相互作用.其中,i、j表示不同分子,a、b表示不同原子,kr和fθ为力常数,r、θ和φ为体系的真实键长、键角和二面角值,req、θeq为平衡时的键长、键角值.V1、V2、V3表示二面角的Fourier展开系数.σia,jb、εia,jb分别表示第i个分子中原子a和第j个分子中原子b之间的碰撞直径和势阱深度,fij为常数.qm和qn分别表示第m和第n个位点所带电荷.kmn为静电相互作用校正系数,①当位点m和n处于1-2或1-3关系时,kmn=0;②当两位点处于氢键作用区域(HBIR)时,kmn=kHB,kHB为氢键拟合函数,引入它可以防止2个原子之间的电荷过度极化,其具体公式如下所示:

(2)

其中，A、B、C、D为相关参数,Rlp,H为孤对电子和氢原子间的距离.③当两位点在其他区域时,kmn=0.57.ABEEMσπ/MM浮动电荷力场将分子划分为原子、键以及孤对电子位点,并且各位点电荷会随环境的改变而发生变化.

1.3 ABEEMσπ/MM参数

ABEEMσπ/MM参数包括力场参数和电荷参数.力场参数中的键长伸缩振动、键角弯曲振动等参数来自CHARMM36力场.电荷参数包含价态硬度和价态电负性.根据QM计算得到的模型分子ETMA、MAS、DMP的稳定结构和电荷分布,调节优选相关参数,使由ABEEMσπ/MM势能函数公式计算得到的模型分子结构、电荷分布等与QM结果吻合,优选后的参数列在表1中.进一步应用ABEEM/MM势能函数计算磷脂分子POPE的结构和电荷分布,检验参数的合理性.优选得到的POPE力场参数分别列在表2～表4中.

表1 小分子MAS、DMP、TMA的静电参数

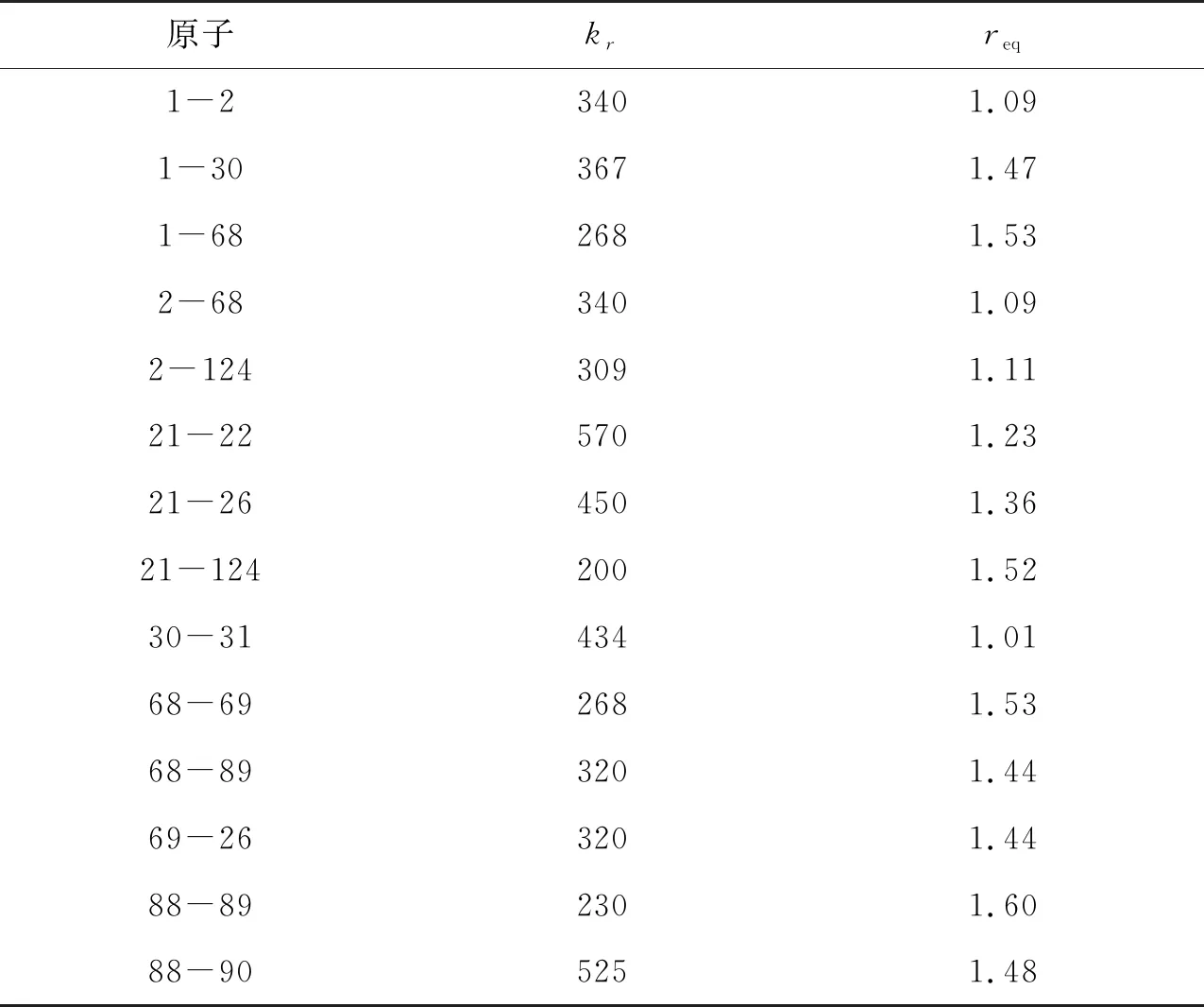
表2 POPE分子的键长伸缩振动参数

表3 POPE分子的键角弯曲振动参数

表4 POPE分子的二面角扭转势能参数

2 结果与讨论

2.1 小分子的几何构型和电荷分布

应用公式(1)计算模型小分子MAS、DMP和ETMA的结构和电荷分布,获得的稳定结构与QM结果进行比较.表5给出了3种分子在两种方法下的键长、键角以及二面角的平均偏差(AAD)、均方根偏差(RMSD)和相对均方根偏差(RRMSD).其中,偏差最大的DMP的键长、键角、二面角的AAD、RMSD、RRMSD分别为0.021 9、0.003 5 nm和2.59%,2.39°、3.48°和3.16%,2.61°、3.26°和2.87%.总体来说,ABEEMσπ/MM力场方法计算结果与QM方法结果有较好的一致性.

表5 ABEEMσπ/MM与QM方法优化的模型小分子的结构对比

图1为ABEEMσπ/MM方法和QM方法计算得到的3种分子电荷分布的线性相关图,可以看出电荷分布的线性相关系数为0.972 8,斜率接近于1,截距接近于0,两者获得的电荷分布具有良好的一致性.

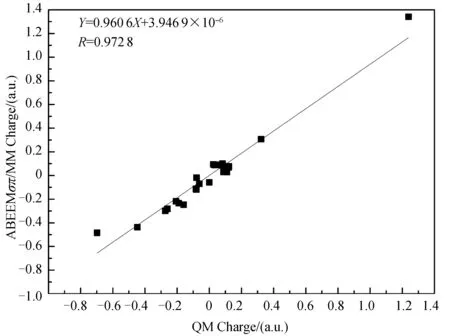
图1 ABEEMσπ/MM与QM计算的DMP、MAS和 ETMA的电荷分布的线性相关图Fig.1 The linear correlation of charge distributions of DMP,MAS and ETMA between ABEEMσπ/MM and QM

2.2 POPE分子的结构和电荷分布

表6为ABEEMσπ/MM与QM方法得到的POPE分子的键长R(nm)、键角θ(°)、二面角τ(°)的比较.结果表明,ABEEMσπ/MM与QM结果符合很好.其中，二面角的AAD最大为0.344 0°,RMSD为0.507 2°,RRMSD为0.452 0%.

表6 ABEEMσπ/MM与QM方法得到的POPE分子稳定结构的对比

图2为ABEEMσπ/MM与QM方法计算得到的POPE分子的电荷分布的线性相关图.从图中可以看出二者线性相关很好,斜率为1.024 0,线性相关系数为0.981 3,截距趋近于0.

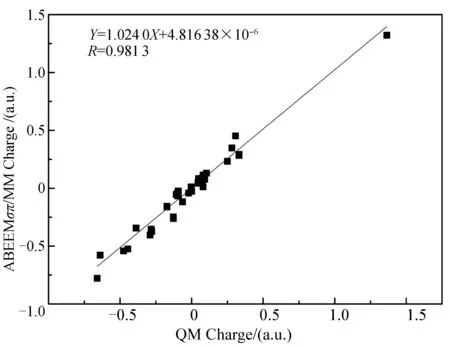
图2 ABEEMσπ/MM与QM计算POPE电荷分布的线性相关图Fig.2 The linear correlation of charge distributions of POPE between ABEEMσπ/MM and QM

3 结论与展望

建立了POPE分子的ABEEMσπ/MM浮动电荷势能函数,基于QM计算结果,优选确定相关参数.应用该势能函数计算获得的POPE分子的结构和电荷分布与QM结果符合很好,表明本文初步建立的POPE分子的ABEEMσπ/MM力场的合理性和可靠性.此项研究为进一步将ABEEMσπ/MM推广到其他磷脂分子体系,建立可用于复杂生物分子体系的磷脂分子的浮动电荷分子力场打下了基础.