基于不计入巡航变形影响的刚体载荷弹性修正方法研究

王建礼，孙明哲，周 彬

(中国商用飞机有限责任公司北京民用飞机技术研究中心, 北京 102209)

适航规章规定民用飞机的临界载荷工况是2.5g和-1.0g[1]，且新型飞机的临界载荷必须由风洞试验数据产生，除非此新型飞机有以往类似型号设计经验，才可使用计算流体动力学(computational fluid dynamics,CFD)方法计算临界载荷。此外，由于飞机结构的弹性特征，必须考虑各部件弹性变形对气动载荷分布的影响。然而风洞试验通常采用以巡航外形为基准的刚体模型，其测得的数据是1g巡航状态下的压力分布，如果直接采用这套数据对飞行载荷进行静气动弹性修正，将导致飞机结构过度变形，基于此问题本文提出一种基于刚体风洞模型试验数据的弹性修正方法。

1 刚体载荷弹性修正方法

基于巡航外形下飞机刚体风洞试验模型数据的弹性修正方法流程如图1所示，主要步骤如下：1)获取飞机风洞试验数据，对巡航外形进行反向变形修正，得到型架外形；2)对每一飞行状态下的数据进行修正，得到型架外形上的气动压力分布系数；3)根据修正得到的型架外形气动数据，进行弹性载荷修正；4)筛选每一状态下的弹性载荷，得到对结构影响最大的关键载荷，作为结构设计的输入条件。

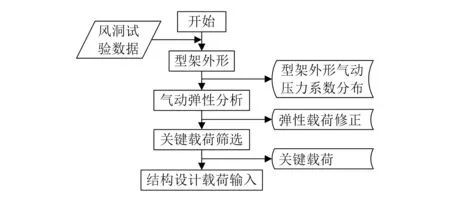
图1 风洞模型刚体载荷弹性修正方法流程

本文采用的研究方法包括气动力影响系数矩阵、气动结构插值、静气动弹性分析、型架外形修正和关键载荷筛选。

1.1 气动力影响系数矩阵

飞机载荷计算需要对大量飞行工况(不同马赫数、攻角、高度、载重状态)进行分析。为了提高计算效率，本文将刚体风洞测压数据按照高阶面元法的方式存储成气动力影响系数矩阵[2]，对于相同工况下的载荷计算只需读取该矩阵数据即可进行，从而大幅度节省计算时间。

1.2 插值方法

气动弹性分析涉及气动和结构两个学科，二者建模有着明显差异：气动数据点建立在模型表面，结构数据点则建立在内部承载部件上，两者之间数据传递的精度直接影响着气动弹性分析的准确性。本文根据飞机不同区域的建模特点采用3种不同的插值方法[3-4]，即无限平板插值法、薄板插值法和梁插值法，将结构位移插值到气动模型上，并应用最小二乘法对插值曲线进行拟合以保证其光顺性。此外，这些插值方法也可以用于刚体风洞试验数据到气动模型的转换。

1.3 静气动弹性分析

弹性飞机变形后将导致气动载荷重新分布，直接影响载荷的计算精度[5]。考虑气动弹性效应的牛顿第二定律方程可表示为[3]：

(1)

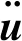
可以看出全机上的总力由三部分构成：气动力、弹性力和惯性力。弹性力大小与动压紧密相关，动压越大，即速度越高或者密度越大(高度越低)，静气动弹性效应越明显。

1.4 型架外形气动压力分布修正

在计算弹性载荷之前，需要将巡航外形上的一系列风洞试验数据修正到型架外形上[2,6-7]。

1)根据1g巡航压力系数分布进行静气动弹性正向变形，结构质量应选取巡航状态下的半油和半商载工况。

2)将正向变形量反向施加到结构模型上即可得到型架外形。

xjig=xcruise-Φe·ζ

(2)

式中：xjig为型架外形坐标矩阵；xcruise为巡航外形坐标矩阵；ζ为每一阶弹性自然模态的变形量。

3)型架外形压力系数分布修正按照下式计算：

Cp,jig=Cp,cruise-AIC·Φe·ζ

(3)

式中：Cp,jig表示型架外形的压力系数分布；Cp,cruise表示巡航外形的压力系数分布；AIC,Φe和ζ3个矩阵相乘的结果为弹性变形引起的压力系数修正量。

1.5 关键载荷筛选

在飞行包线内挑选产生极限载荷的机动工况作为结构设计的约束条件，具体步骤如下：1)确定载荷观察点位置，选择此处的弯矩、剪力和扭矩作为关键载荷筛选的指标；2)根据刚体压力分布数据修正结果，计算飞行包线内所有马赫数、攻角、高度组合下达到2.5g和-1.0g机动时各个观察点处的弹性载荷，包括弯矩、剪力和扭矩；3)从弹性载荷中挑选极限值所对应的飞行工况作为关键载荷工况，完成关键载荷筛选。

2 实例分析

以某型号飞机的风洞试验数据为依据，利用上述研究方法，验证方法的适用性和精确度。

2.1 插值方法验证

本文首先验证结构模型到气动模型的转换。针对飞机不同域结构建模的特点，选取插值方法如下：机翼采用薄板插值法，机身采用梁插值法，平尾、垂尾、升降舵和方向舵采用无限平板插值法。图2为第1阶和第6阶模态下全机的变形情况(变形量放大5倍)，通过查验未出现奇点，表明插值方法的准确性。

图2 飞机弹性自然模态 图3 44%展长处数据对比 图4 82%展长处数据对比

其次验证风洞试验数据到气动分析模型数据的转换。机翼、垂尾和平尾的前缘曲率较大，采用三维薄板拟合插值方法；机身、发动机和吊挂处采用三维薄板插值方法；其他部分采用无限平板拟合插值方法。

马赫数为0.785、飞行攻角为5.0°工况下，44%和82%展长截面上插值得到的气动压力系数分布与风洞试验数据的对比情况如图3，4所示。

虽然因为风洞试验数据本身存在的误差(个别测试点数据跳跃)会导致一些位置存在由于拟合引起的精度损失，但并不影响总力积分。图3和图4中两条曲线基本吻合，可以认为根据这些插值数据计算所得的气动力是准确的。

2.2 静气动弹性效应分析

图5给出了马赫数为0.785、高度为12 100 m时，刚体风洞试验数据经过静气弹修正和未修正的升力系数曲线对比，可以看出修正后的升力系数略高于直接采用刚体风洞试验数据得到的升力系数。这表明如果按照风洞数据进行分析会导致结构过度变形，从而引起有效攻角变小，致使气动力降低，因而得到的载荷也会偏小。

图5 静气弹修正对风洞试验数据的影响 图6 44%展长处数据对比 图7 82%展长处数据对比

2.3 型架外形气动压力系数修正

图6和图7分别为巡航工况下，44%和82%翼展截面的型架外形压力系数修正与风洞数据对比情况。可以看出，相比于风洞数据，型架外形上的压力系数有所增加，这是由于巡航外形卸载后机翼前缘相对于后缘发生扭转，导致局部攻角增大，使得卸载后的气动力变大。

2.4 关键载荷筛选

本文以飞机达到2.5g过载时关键载荷的筛选为例介绍具体流程。

首先选择载荷观察点。通常对于大型民用飞机而言，机翼根部承受机翼上所有气动力和惯性力的合力，吊挂处承担发动机推力带来的扭矩，外侧机翼会承受由副翼偏转造成的较大扭矩，因此选择这3个特殊位置为载荷观察点。

对于飞行包线内的每一飞行工况，将修正后的风洞试验数据插值到气动模型上，并进行静气动弹性分析，计算配平后的过载系数和弹性载荷，然后挑选出接近2.5g过载时的所有飞行工况，筛选出每个工况下各个载荷观察点弯矩、剪力和扭矩的极值，其所对应的工况作为初始关键载荷工况。此时可以发现，因为风洞试验数据选择的工况有限，并不能保证得到的关键载荷工况能够完全达到2.5g，所以最后还需要通过调节升降舵将过载配平到2.5g，在这一状态下的弹性载荷即认为是关键载荷。-1.0g过载的关键载荷也可以采用相同的方法得到。

表1节选了0.7马赫工况下达到2.5g过载的飞行工况以及翼根位置的弯矩、剪力和扭矩值，其中绝对数值最大的即为载荷极值。对于其他各飞行马赫数工况均按照表1的方式找出极值，通过对比筛选出所有马赫数下的载荷极值就可以得到关键载荷工况。表2列举了最终筛选出的关键载荷工况，这些工况下的载荷即为结构设计的输入条件。

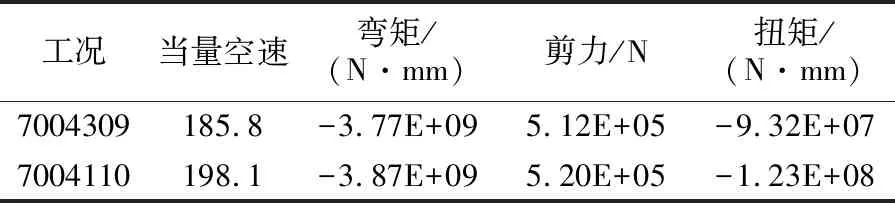
表1 0.7马赫工况翼根处2.5g关键载荷工况

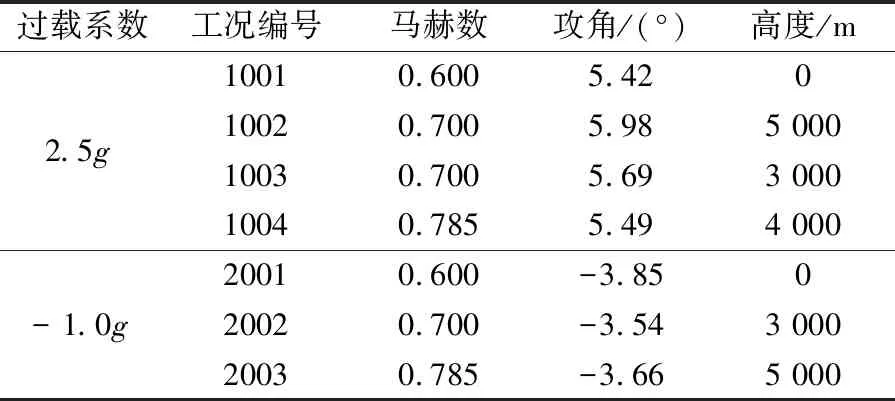
表2 关键载荷工况汇总

2.5 关键载荷筛选验证

关键载荷筛选最关注的问题就是选取的结果能否充分代表飞机飞行中承受的极限载荷。本节将分析关键载荷筛选方法的合理性。

图8和图9给出了马赫数为0.6时所有飞行工况下剪力和弯矩沿机翼翼展不同站位处的分布情况，图中菱形图例区域表示2.5g和-1.0g过载范围外的飞行工况载荷分布，方形图例区域表示2.5g和-1.0g范围内的载荷分布，圆形图例区域则表示按照2.5g和-1.0g筛选出的载荷分布。可以看到，利用翼根观测点选取的关键载荷工况在机翼其他展向位置也基本处于极值状态，仅在有惯性力发生突变的位置(吊挂位置)和外侧机翼(副翼偏转位置)略有不同。由此可见，文中选取翼根、吊挂和外侧机翼3个载荷观察位置已经可以充分反映全机各个位置的载荷极限状态，由此3个位置筛选得到的极限载荷即为关键载荷。

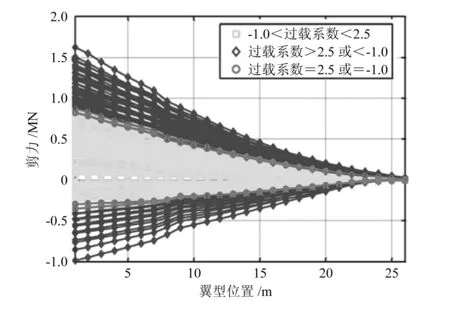
图8 马赫数为0.6时各工况剪力沿翼展分布

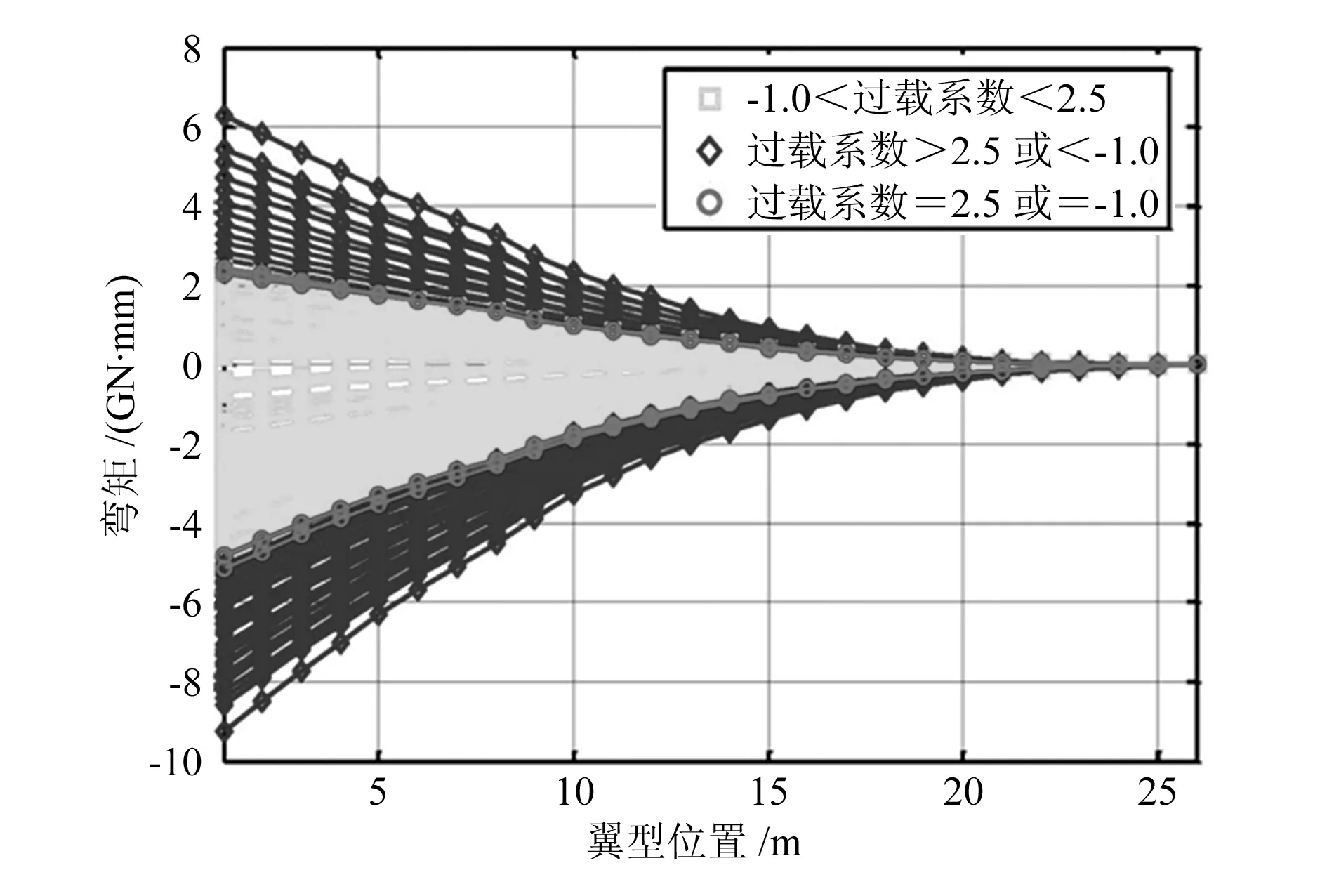
图9 马赫数为0.6时各工况弯矩沿翼展分布

3 结论

本文将巡航外形上的刚体风洞试验数据修正到型架外形上，再通过静气弹修正得到弹性载荷，最后从中筛选出关键载荷，并以某型号飞机的风洞试验数据为依据对方法进行了验证，得到以下结论：1)插值方式的选取对载荷计算精度影响较大，对飞机不同区域需要根据其特点选取合适的插值方法；2)静气动弹性效应对载荷计算影响显著，必须予以考虑；3)直接采用风洞试验数据进行静气弹分析，将会导致结构过度变形；4)根据机翼根部、吊挂位置和外侧副翼3个载荷观察点筛选极限值得到关键载荷，此方法不会造成漏选；5)需要通过后续的飞行试验数据对计算出的弹性载荷进行校核。