MW级风力发电机塔筒门框优化设计
2020-12-29晁贯良祝蕴龙孙刚峰张文彬
晁贯良,祝蕴龙,孙刚峰,张文彬
(1.许昌许继风电科技有限公司,河南 许昌 461000)(2.国家电投集团河南新能源有限公司,河南 郑州 450001)
塔筒是风力发电机的主要承载部件,其将风力发电机与地面连接使风力发电机支撑在有利的高度以达到最经济安全的风能利用。塔筒不仅要承受风力发电机的质量,还必须承受吹向风力发电机和塔筒的风载,以及风力发电机运行中产生的动态载荷。塔筒必须具有足够的抗疲劳强度,能够承受风轮引起的振动载荷,在风力发电机设计使用寿命期间满足各种复杂环境下强度、刚度和稳定性的要求[1]。
为了方便人员及设备进出,塔筒底端一般需要开设门洞,这使得塔筒底端的强度和刚度被大大削弱,实际工程中通常在门洞处增设与筒壁通过全熔透T型焊缝连接的环形筋板进行补强[2]。由于门框附近的应力集中现象以及焊缝容许疲劳应力幅较低,需要门框几何形状、筋板厚度及以及筒壁厚度满足一定关系以降低筒壁与环形筋板连接处的最大应力、门洞缺口因子和疲劳应力幅,使塔筒门框满足极限、疲劳和屈曲的设计要求[3]。
本文针对MW级风电机组100 m塔筒门框初始设计方案进行工程分析,以塔筒门框以及门框附近塔筒壁强度为约束目标,利用Workbench软件进行塔筒门框结构优化计算;根据EN1993-1-6规范进行门框屈曲强度校核;利用有限元软件ANSYS对该优化结构进行有限元建模,并基于线性累积损伤理论对门框优化结构进行疲劳强度校核,得到塔筒门框以及门框附近塔筒壁的最大疲劳损伤;最后根据工程焊接要求进行塔筒壁厚布置,确定最优的塔筒门洞截段设计方案。
1 几何模型
某轮毂高度为100 m的MW级双馈型风力发电机组,其塔筒由5段10~30 m的锥筒用法兰连接而成,底部开设有门洞,采用传统跑道形加筋板门框。塔筒门洞截段的结构尺寸如图1所示,根据工程算法,针对塔筒焊缝、塔筒屈曲、塔筒涡激以及塔筒门洞截段顶部法兰强度进行计算,结果均满足极限强度设计要求。塔筒门框附近由于门洞的缺失效应,需要对其进行应力修正,本文研究的门框符合GL规范6.6.7.2修正要求,可以采用GL规范的开口系数进行修正,参考EN1993-1-6进行屈曲计算[4-5],结果表明门框区域满足屈曲强度设计要求。

图1 塔筒门洞截段
2 有限元分析
采用有限元软件ANSYS对塔筒门框的受力性能进行分析,其中选取的总体坐标系是GL规范中通用的塔底坐标系:x轴沿风轮轴的水平方向,z轴沿塔筒轴线竖直向上,y轴沿水平方向,并按照右手定则确定。弯矩对塔筒的影响最为明显,一般情况下y方向弯矩My往往比x方向弯矩Mx数值大,因此设计塔筒时门框应垂直于主风向布置。为避免边界条件对门框应力分布的影响,采用塔筒门洞截段(包括底法兰)作为分析对象。为了方便对塔筒门洞截段底部施加载荷,在底部法兰中心建立参考点并与塔筒门洞截段顶部耦合,塔筒门洞截段底部法兰处即0 m位置载荷施加在参考点上。塔筒门洞截段底部载荷有16个极限工况,见表1,分析塔筒时,一般选取组合弯矩最大的工况为危险工况,这里选取的是最大弯矩Mxy_max极限载荷工况。
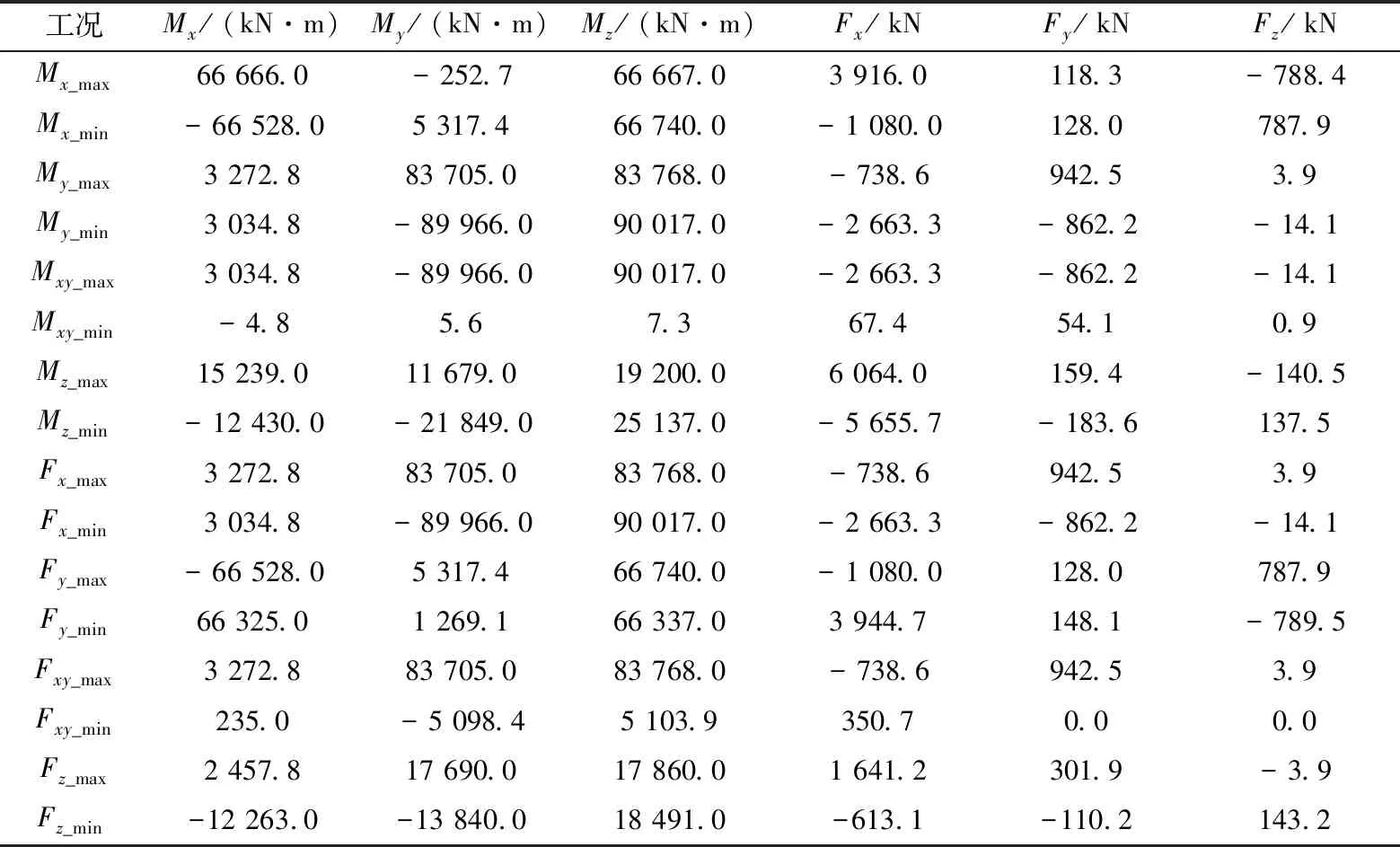
表1 塔底载荷
塔筒采用低合金高强度钢Q345,材料性能见表2。根据GL规范,在分析极限强度时,金属材料应考虑1.1倍的局部安全系数。

表2 Q345材料性能
在最大弯矩Mxy_max极限载荷工况下,门框区域等效应力云图如图2所示。从图2(a)中可以看出,塔筒壁的最大等效应力为332.66 MPa,出现在门框内面与塔筒壁连接处并集中于门框椭圆弧外侧区域。从图2(b)中可以看出,门框最大等效应力332.16 MPa,出现在门框外面并集中于门框与塔筒壁连接处的椭圆弧处;塔筒门框和塔筒门框附近塔筒壁的等效应力均大于许用应力,不满足强度设计要求,需要对其进行结构优化。

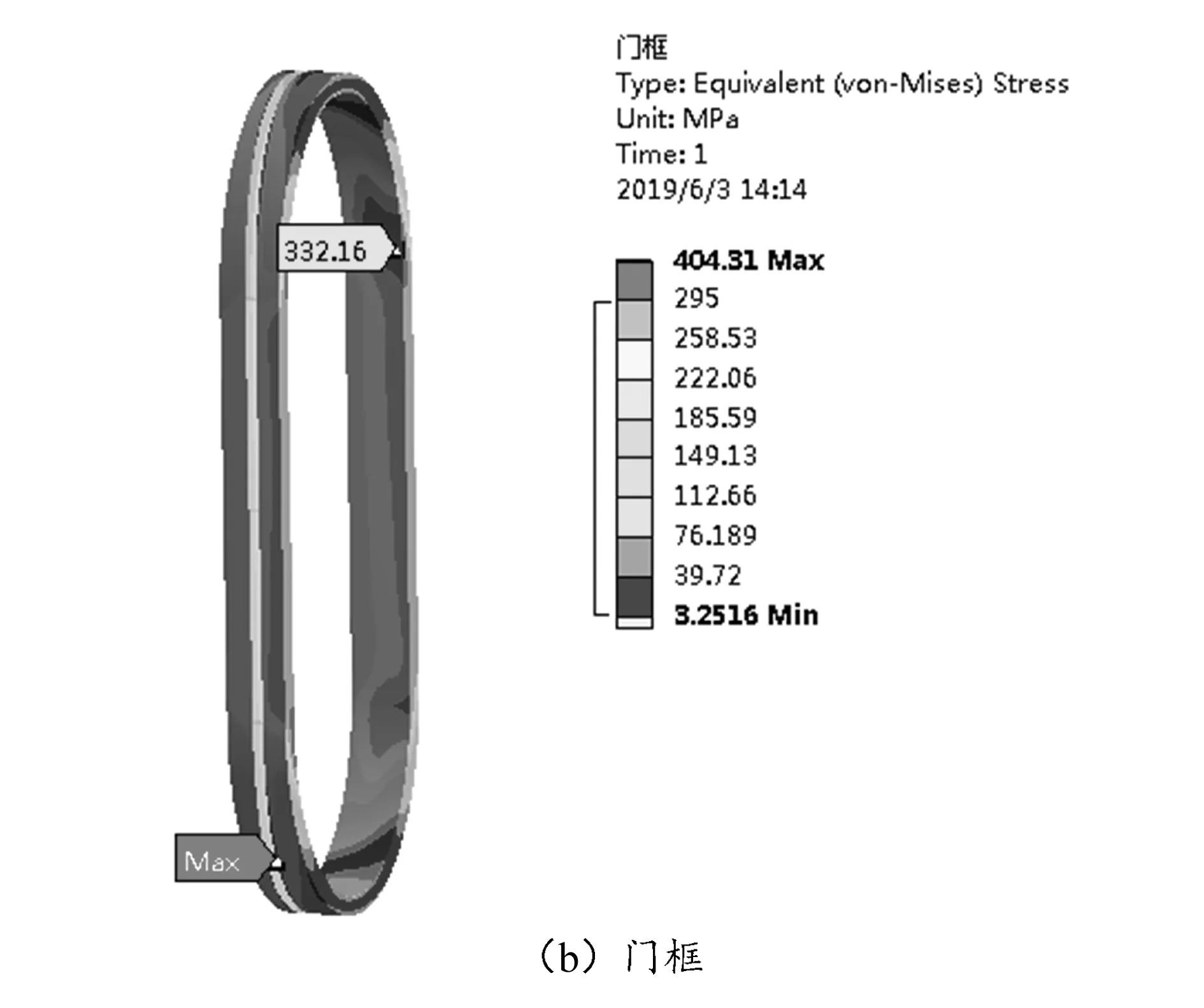
图2 原方案门框区域有限元结果
3 塔筒门洞参数化优化设计
塔筒门框由于门洞缺失的影响存在较大的应力集中现象,简单的工程算法已不能满足强度校核的需要,因此采用有限元软件Workbench平台中的参数化模块Design Xplorer(简称DX)对塔筒门框进行参数化建模分析。基于CAE(computer aided engineering)技术进行结构优化设计的基本流程如图3所示[6-7]。
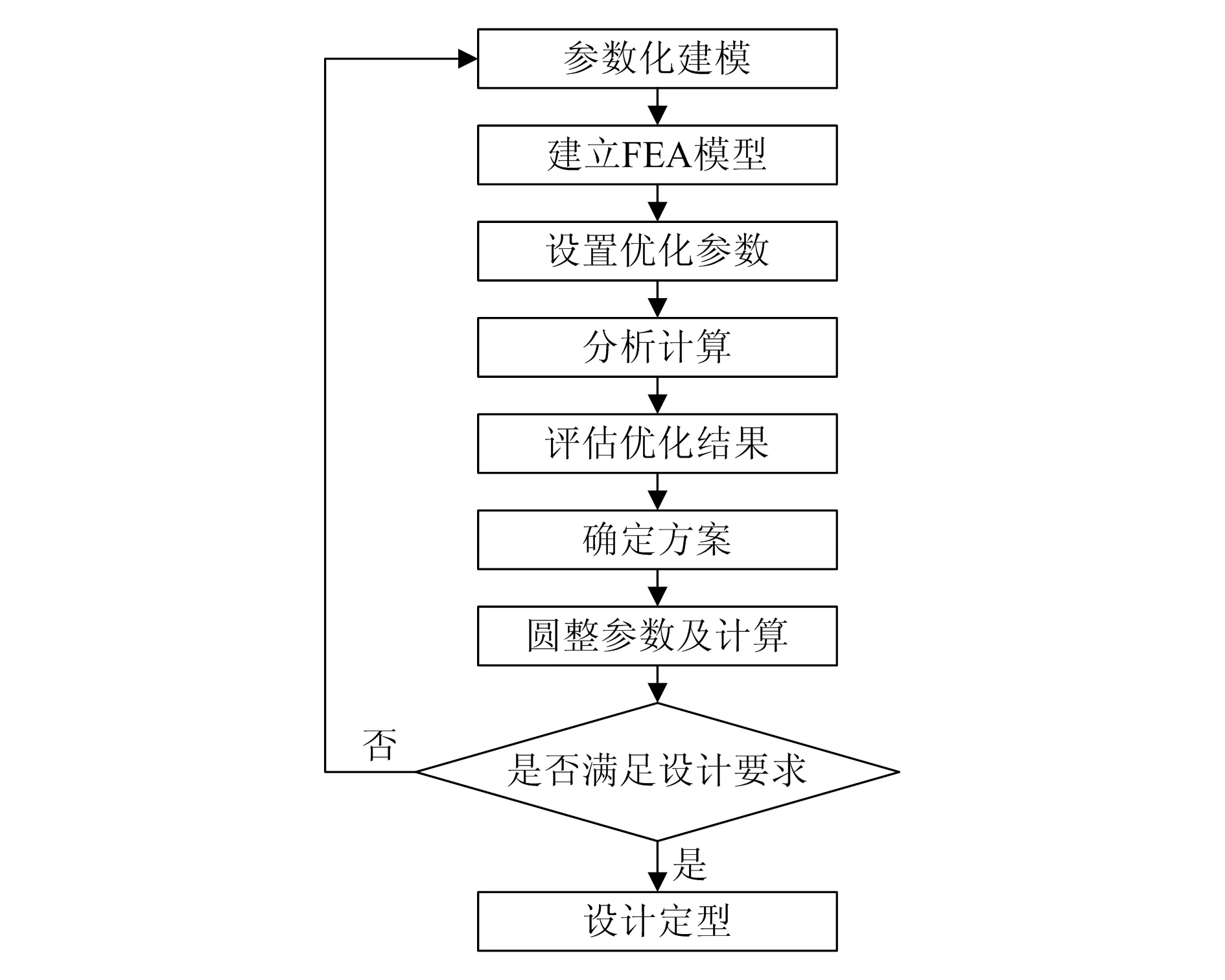
图3 结构优化设计流程
3.1 塔筒模型
塔筒门框不仅需要方便人员及设备进出塔筒,还需要为变流器风冷风扇提供安装位置;考虑门锁的操作空间,塔筒门洞最小尺寸及布置如图4所示。根据塔筒门洞截段建模过程,将影响门框强度的7个参数作为优化分析的输入参数,即塔筒壁厚、门框直线长度、门框内壁宽度、门框椭圆长轴半径、门框厚度、门框外面与塔筒外壁距离以及门框内面与塔筒内壁距离。
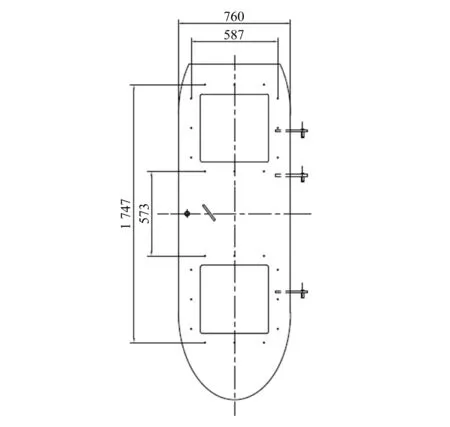
图4 塔筒门洞限制尺寸
3.2 参数化优化分析
根据塔筒门框优化分析的初始模型可知,塔筒壁厚为36 mm,门框直线长度为1 340 mm,门框宽度为780 mm,门框椭圆长轴半径为600 mm,门框厚度为60 mm,门框外面与塔筒外壁距离为43 mm以及门框内面与塔筒内壁距离为127 mm。优化分析的输入参数变化范围见表3,首先将门框及塔筒壁最大等效应力作为响应参数,采用中心复合方法生成157个设计点,利用设计点进行有限元极限强度分析;然后根据157个有限元分析结果生成响应面;最后设置输入参数和输出参数的目标和重要级别,将优化目标门框和塔筒壁最大等效应力设为最小,级别设为最高,从响应面的样本空间中进行筛选,选择最接近设置目标的3个样本值作为最终的候选方案。
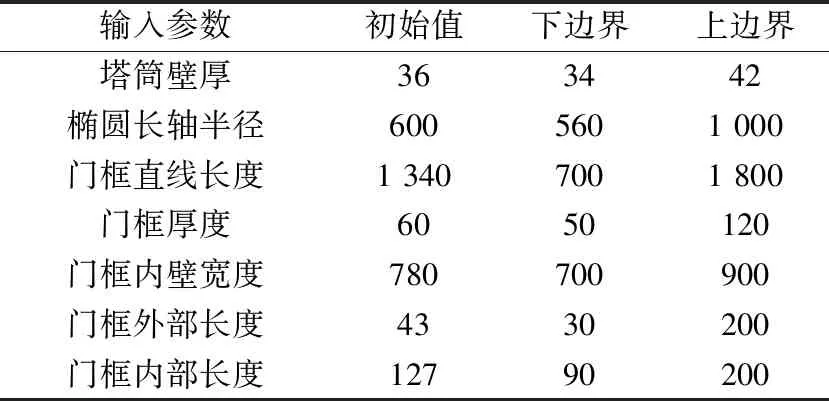
表3 输入参数边界列表 mm
3.3 灵敏度分析
灵敏度分析是指研究与分析一个系统模型的状态变化对系统参数变化敏感程度的方法。该分析方法可以为结构优化提供一个有效的优化思路,通过灵敏度分析可以确定环境条件变化时对优化解的影响。门框及其附近塔筒壁区域最大等效应力对各设计变量变化的局部灵敏度如图5所示。
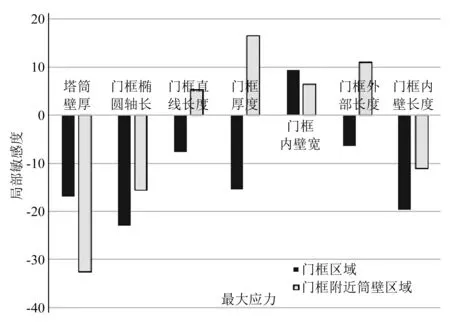
图5 灵敏度分析结果
根据图 5可以得到以下结论:
1)门框最大等效应力与塔筒壁厚度、门框椭圆长轴半径、门框直线长度、门框厚度、门框外部长度以及门框内部长度呈负相关;塔筒壁越厚或门框椭圆长轴半径越大,门框等效应力越小,塔筒椭圆长轴半径对门框等效应力影响程度最大。
2)门框附近塔筒壁区域最大等效应力与塔筒壁厚度、门框椭圆长轴半径及门框内部长度呈负相关;塔筒壁越厚或门框椭圆长轴半径越大,门框附近塔筒壁等效应力越小;塔筒壁厚对门框附近塔筒壁等效应力影响程度最大。
3)门框附近塔筒壁及门框区域等效应力与塔筒壁厚、门框椭圆长轴半径及门框内部长度均呈负相关。当增大这3个输入参数时,门框附近塔筒壁及门框区域等效应力均可以得到改善。
4)门框附近塔筒壁及门框区域等效应力与门框内壁宽度(开口尺寸)均呈正相关。当减小塔门框内壁宽度时,门框附近塔筒壁及门框区域等效应力均可以得到改善。
5)门框附近塔筒壁等效应力与门框直线长度、门框厚度、门框内壁宽度及门框外部长度均呈正相关;门框等效应力与门框直线长度、门框厚度及门框外部长度均呈负相关。
3.4 响应面分析
响应面分析法是通过多元二次回归方程拟合因变量与多个自变量之间的函数关系,通过对回归方程的分析得到最优输入参数,以解决多变量问题的一种统计方法。响应面运用图形技术将输入变量与相应变量之间的函数关系显示出来,方便观察、选择输入变量中的最优化条件。根据输入参数与响应参数的关系曲线可以得到如下结论:
1)门框椭圆长轴半径与门框等效应力关系如图6所示,当门框椭圆长轴半径为760 mm左右时,门框附近塔筒壁与门框等效应力基本一致。

图6 门框椭圆长轴半径与等效应力关系
2)门框厚度与门框等效应力关系如图7所示,当门框厚度为78 mm左右时,门框附近塔筒壁与门框等效应力一致。
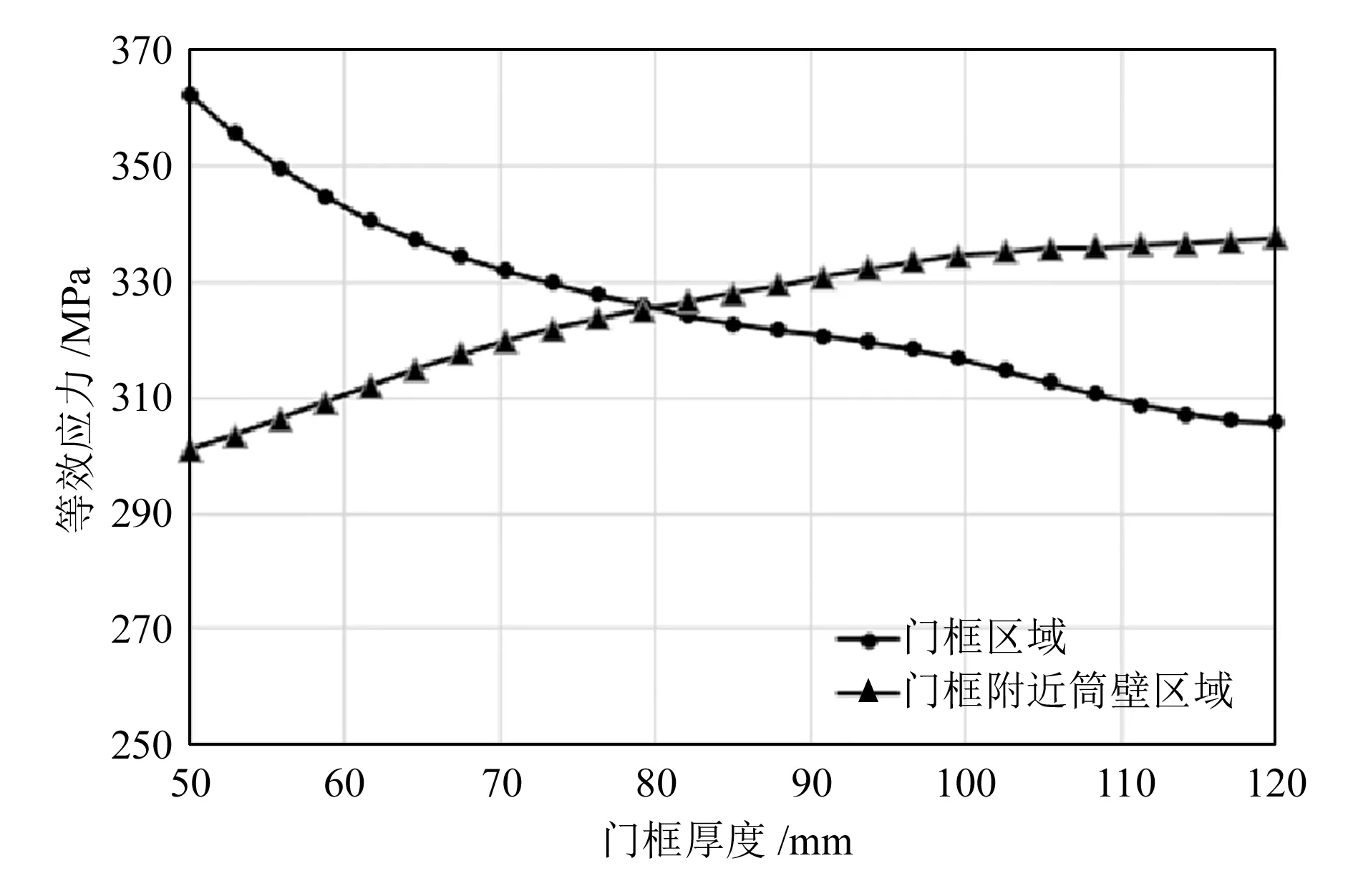
图7 门框厚度与等效应力关系
3)门框内壁宽度与门框等效应力关系如图8所示,当门框内壁宽度为780或850 mm左右时,门框附近塔筒壁与门框等效应力一致,门框内壁宽度与门框等效应力关系如图8所示。
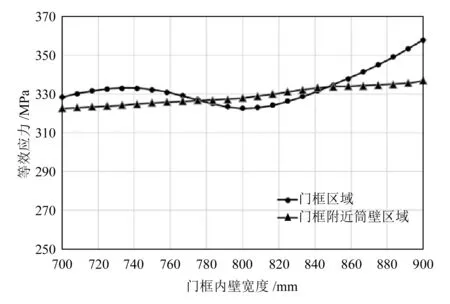
图8 门框内壁宽度与等效应力关系
4)门框外壁长度与门框等效应力关系如图9所示,当门框外部长度为100或160 mm左右时,门框附近塔筒壁与门框等效应力一致。

图9 门框外部长度与等效应力关系
5)门框内部长度与门框等效应力关系如图10所示,当门框内部长度为130或155 mm左右时,门框附近塔筒壁与门框等效应力一致。
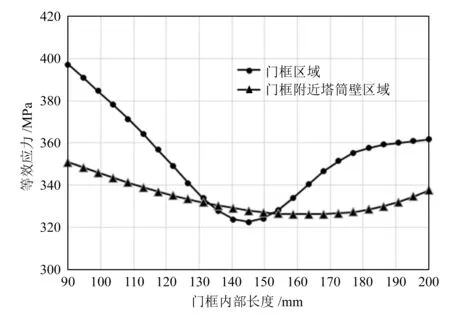
图10 门框内部长度与等效应力关系
3.5 优化结果
针对多目标优化问题,各优化目标之间一般不能同时达到最优,因此得出的是一系列有效解,此类有效解称为pareto解。多目标优化问题就是在一系列pareto解中找到最有效的几个解,根据工程实际需要,从中选择最满意的参数解。本文基于多目标遗传算法,采用Workbench软件中的目标驱动优化模块,对目标函数进行优化求解。经过优化分析,门框尺寸参数的3组推荐解见表4。
由于多目标遗传算法是基于响应面进行的插值计算,得到的推荐解并非真实解,存在一定的误差,需将推荐点作为设计点,圆整后重新计算。由表4可知,候选点1不满足GL规范要求的塔门设计要求;候选点3相对于候选点2门框位置最大等效应力小,考虑到安全性因素,将候选点3作为最优设计点。将候选点3中的输入参数进行圆整见表5,并针对候选点进行静强度计算。

表4 推荐解
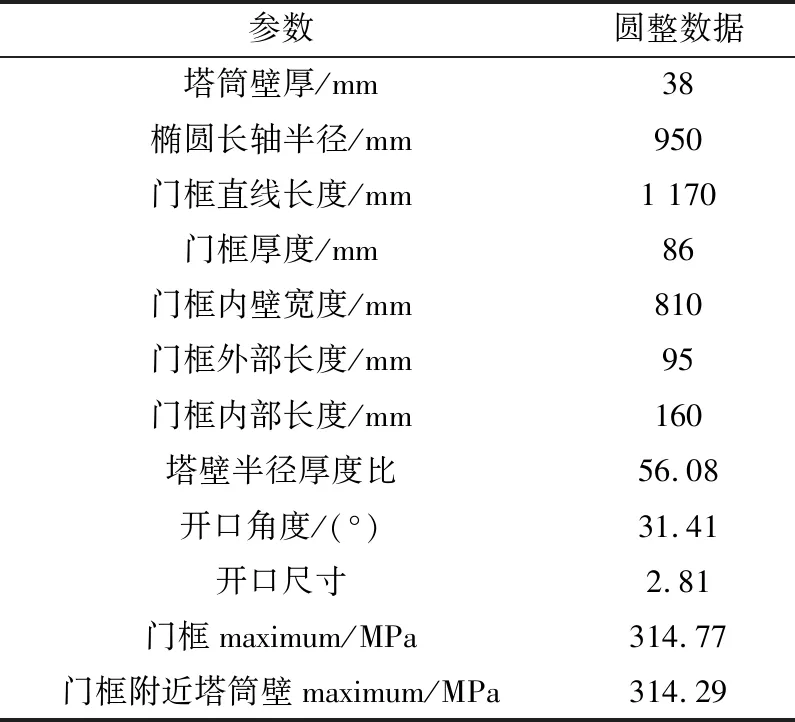
表5 候选点3圆整
本文中门框附近塔筒壁最大应力代表的是应力集中下的焊趾应力,根据IIW规范,焊趾应力需要根据表面外推法进行线性插值,焊缝插值应力结果为279.18 MPa;门框位置的最大应力代表的是包含焊趾点的门框表面应力,实际值需排除焊趾应力奇异点,门框真实应力结果为275.64 MPa,计算结果如图11所示,可知门框及焊缝均满足强度设计要求。

图11 优化方案门框区域有限元结果
4 稳定性分析
稳定性分析主要是研究结构在特定载荷作用下从稳定平衡状态到不稳定状态下的临界载荷和屈曲形态。针对受压结构,随着外力F的增大,结构抵抗横向变形的能力逐渐减小。当外力F达到临界作用力时,总体结构刚度接近于零,位移无限增加,结构丧失稳定性,发生屈曲破坏[8-9]。
风力发电机组中塔筒是一种偏心受压的薄壁结构,容易引起失稳破坏。塔筒不仅需要满足强度设计要求,还需要满足结构稳定性要求。塔顶坐标系下,作用于塔筒的载荷可分解为沿坐标轴的3个分力和3个力矩,其中作用在塔筒的轴向力Fz和力矩Mxy对塔筒屈曲稳定性影响最大。值得注意的是,力矩Mxy是塔筒截面弯矩Mx和My的力矩组合与塔筒沉降引起的附加力矩之和。当外载荷引起的压应力超出某一截面屈服极限时,结构局部失稳,导致塔筒发生破坏。由于塔筒底部开设有门洞,削弱了塔筒的整体性,在此部位容易产生应力集中,造成局部失稳,因此需要对塔筒门洞进行局部稳定性分析。
屈曲稳定性计算公式如下:
δ=2arcsin(b1/r)
(1)
SRF=C1σxS,R,d-DIN/σ
(2)
式中:δ为开口角度;b1为塔筒门洞开口宽度;r为塔筒门洞恒定横截面半径;SRF为屈曲稳定性系数;C1为折减系数;σxS,R,d-DIN为DIN18800-4中径向临界屈曲应力;σ为门洞计算屈曲应力。
通过计算可得:径厚比r/t=56.08≤160;开口角度δ=31.41°≤60°;开口尺寸h1/b1=2.81≤3;折减系数C1=0.718;临界屈曲应力σxS,R,d-DIN=283.47 MPa;设计屈曲应力σxS,R,d=C1σxS,R,d-DIN=203.54 MPa;门洞计算屈曲应力σ=218.09 MPa;SRF=0.93<1,塔筒门洞不满足屈曲设计要求。将塔筒门洞上部塔筒壁厚由30 mm增加至34 mm,优化后的塔筒门洞截段如图12所示,σ=192.96 MPa,SRF=1.05>1,结果表明,塔筒门洞的屈曲稳定性能够满足塔架的安全运行要求。
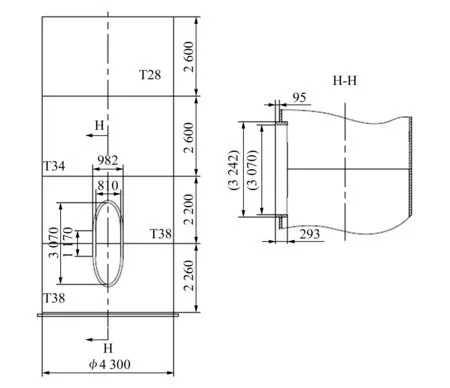
图12 塔筒门洞截段
5 疲劳强度分析
根据GL规范,对风机中主要用于动态载荷的金属部件需进行疲劳分析。焊缝疲劳强度可采用名义应力法、热点应力法和切口应力法进行分析[10-11]。针对门框与塔筒壁的焊缝连接,由于存在门洞缺口效应,应力状态比较复杂,因此焊缝疲劳强度采用热点应力法进行分析。疲劳分析时,推荐S-N曲线详细分类DC按照参考标准EN1993-1-9或IIW规范进行,其中塔架和基座适用EN1993-1-9,而机舱内金属部件适用IIW规范。根据EN1993-1-9规范中提供的焊接结构形式,塔筒门洞焊接材料S-N曲线的详细分类DC选取100,即循环次数为2×106次下应力范围表征的疲劳强度为100 MPa。塔筒门框焊趾处的应力可通过表面外推法进行线性插值提取,通常情况下,塔筒的壁厚较门框厚度薄,这里仅校核塔筒壁焊趾处的疲劳强度。考虑到焊趾应力的多轴性,选择临界平面法的正应力进行疲劳应力分析。通过雨流计算并结合S-N曲线,运用Palmgren-Miner线性累积损伤理论得到筒壁外侧和内侧热点的损伤值,危险位置发生在塔筒壁内侧,损伤为0.614,小于1,满足20 a使用寿命设计要求。
6 结束语
本文基于参数化建模及工程分析,对某MW级风电机组100 m塔筒门框的结构尺寸、极限强度、屈曲稳定性和疲劳性能进行了研究,结果表明,塔筒壁厚、塔筒门洞椭圆长轴半径、门框内壁长度及门框厚度是塔筒门框结构设计的主要影响因素。本文提出的塔筒门框优化分析方法,优化后的塔筒门框结构不仅满足塔筒屈曲及强度设计要求,而且造价成本较低,因此该方法可作为一种实用的风机门框结构设计手段。
